Исследование влияния массы топлива на дальность полета летательного аппарата

Современный этап развития цивилизации характеризуется переходом к так называемому информационному обществу, в котором в результате процессов информатизации и компьютеризации новые информационный технологии глубоко проникают во все отрасли хозяйства, производство, науку, образование, во все направления интеллектуальной и созидательной деятельности человеческого общества. Информация становится важнейшим ресурсом развития общества наравне с сырьевыми и энергетическими ресурсами.

В настоящее время, когда ЭМВ стали необходимым оборудованием научно-исследовательских институтов, конструкторских бюро и заводов, любой выпускник высшего учебного заведения должен обладать знаниями и навыкам, необходимыми для решения практических задач с использование средств и возможностей современной вычислительной техники.

Создание новых сложнейших объектов и устройств, разработка новых технологических процессов производства возможны только на основе всего объема новейшей информации, наиболее современных средств и методов доступа и обработки информации, на основе мощных методов информационного и математического моделирования, методов проектирования и программирования, основанных на применении современных средств вычислительной техники и современных программных средств.

Специфика современной инженерной деятельности приводит к необходимости делать акценты на выработке основ алгоритмического мышления, умении четко формулировать задачу, выявлять исходную и результирующую информацию, приобретать навыки постановки и решения инженерных задач, построения информационных и математических моделей, применять современные технологические и программные средства для решения задач.

Выполнение исследования направлено на овладение практическими навыками использования ЭВМ для численного решения обыкновенных дифференциальных уравнений и систем дифференциальных уравнений в частных производных, проведение вычислительных экспериментов по решению практических задач.

Цель и задачи работы

Цель: исследовать влияние массы топлива, изменяющейся в заданном диапазоне, на дальность полета летательного аппарата (ЛА).

Для достижения заданной цели необходимо решить следующие задачи :

• 1.      Разработать численную модель, алгоритм и программу расчета

• 2.      Выполнить тестирование программы.

• 3.      Провести вычислительные эксперименты и анализ полученных

• 4.       Построить график траекторий полета ЛА.

• 5.      Сделать практические выводы.

неуправляемого полета ЛА на языке программирования СИ++ с заданными начальными условиями по известной математической модели.

результатов.

Этапы решения задачи

Этап 1 Постановка задачи

Исходные данные:

S м *10-3, м2	37	площадь миделевого сечения
m 0 , кг	42	полная масса ракеты с топливом
m t , кг	20..24	масса топлива
t a , с	5	время активного участка траектории
P, кН	38	сила тяги
V 0 , м/с	115	начальная скорость ЛА
α,град	39	угол пуска к горизонту
X, км	?	дальность полета ЛА
С х	0,3	коэффициент аэродинамического сопротивления
g, м/с2	9,8	ускорение свободного падения
ρ в , кг/м3	1	плотность воздуха

Исследовать влияние массы топлива m t на дальность полета X летательного аппарата.

Этап 2 Физическая модель

Запуск ЛА осуществляется с уровня поверхности Земли (координаты точки пуска x₀=0 и y₀=0) со скоростью V=V₀ под заданным углом пуска к горизонту α. Сделаем предположение, что цель ракеты также располагается на поверхности Земли, так что конечная траектория будет иметь координаты x к = X и y к =0.

Для упрощения расчетов сделаем следующие допущения:

• -    все силы, действующие на ракету, приложены к центру ее масс;

• -    в процессе полета ракета не совершает колебательных и вращательных движений;

• -    изменениями значений постоянных величин, таких как плотность воздуха и ускорение свободного падения, в зависимости от высоты пренебрегаем (ρ_в=const и g=const);

• -    участок земли, над которым происходит движение ЛА будем считать плоским;

• -    вращением Земли пренебрегаем.

Траектория движения - это линия движения центра масс снаряда (ракеты) от точки вылета из канала ствола огнестрельного оружия или ствола пусковой установки до точки встречи с целью (точки разрыва).

Движение ЛА по траектории можно описать с использование второго закона Ньютона, устанавливающего взаимосвязь между равнодействующей всех сил F , приложенных к телу определенной массы т, и ускорением О Р :

F = тО                   (1)

На ЛА в процессе движения по траектории действуют следующие силы (рис.1): создаваемая двигателем сила тяги P, направленная по касательной к траектории и совпадающая по направлению с вектором скорости V, аэродинамическая сила Xа, направленная по касательной к траектории в направлении, противоположном вектору скорости, и сила тяжести G.

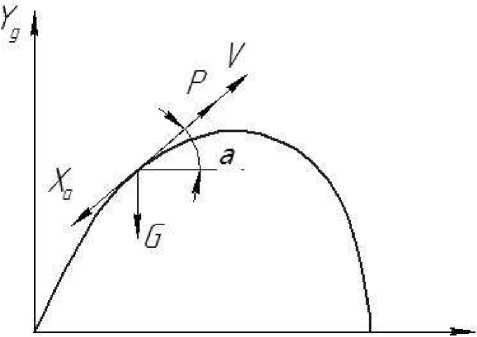
Рис.1 - Силы, действующие на ЛА

Весь процесс движения ЛА можно разделить на два участка: активный (с работающим двигателем) и пассивный (после прекращения работы двигателя).

На активном участке траектории ракета является телом с переменной массой, которая обусловлена выгоранием топлива. Изменение массы характеризуется секундным массовым расходом m = mt I ta.

P

Второй закона Ньютона, записанный в форме F ^ma , справедлив только для тел с постоянной массой. Использование его для тел, масса которых меняется, возможно лишь в случаях разбиения всего расчетного времени на интервалы A t ^ 0 , в течение которых массу тела можно принять постоянной. Расчет траектории движения ракеты сводится к определению параметров траектории и характеристик ракеты, которые являются функцией от времени. В этом случае уравнение (1) можно записать в виде:

m ^p( t ) = P(t ) + Xa ( t ) + G                           (2)

Этап 3 Математическая модель

В соответствии с принятой физической моделью можно представить уравнение (2) в проекциях на оси выбранной системы координат:

m ( t ) a_x = P ( t ) cos( a ( t ) ) - X _a ( t ) cos( a ( t ) )

m ( t ) a_y = P ( t ) sin( a ( t ) ) - X_a ( t ) sin( a ( t ) ) - m ( t ) g

Xа определяется:

X

a

= C x S м

p V ²( t ) 2

P определяется:

P, при t <  t_a

0, при t >  t_a

Массу тела в каждый момент времени можно определить по зависимости:

m ( t ) =

m ₀

- m - t_a 1t ,

при t <  t_a

m₀ - m_t , при t >  t_a

V и a могут быть определены по зависимостям:

dx

Vx = Tt’ dt

V y

dy dt

V =

d 2 xd¥ ax=ttt=;

dt ² dt

I 22

a = a_x + a., xy

d 2 УdV ay = —Г = —” y dt2 dt

Тригонометрические функции угла наклона траектории в каждый момент времени могут быть определены:

V             Vy cos a = -  ; sin a = —

VV

Таким образом, с учетом всех принятых допущений, система уравнений движения ракеты может быть представлена в дифференциальных уравнений первого порядка:

виде системы

^{m ( t} ) ^ax = P ^{( t} ) COS⁽ « ( t ) ) ^- X a ( t ) COS⁽ « ( t ) )

< m(t)ay = P(t)sin(^(t)) - Xa (t)sin(^(t)) - m(t)g х = х 0; y = y 0; t = 0

Этап 4 Численная модель

Полученная система уравнений представляет собой систему обыкновенных дифференциальных уравнений. Решением является функция x(t) , при подстановке которой в это уравнение получается тождество.

При решении подобного рода уравнений в первую очередь необходимо уравнения высших порядков привести к системе уравнений первого порядка.

Рассмотрим приближенное решение дифференциального уравнения первого порядка методом Эйлера:

dy = f ( x , У ),   a ^ x ^ b

• < dx

. У ⁽ a ) = У a

Заменяя производную в окрестностях каждого i-го узла сетки разностными отношением, приходим к следующему виду уравнения:

• -⁺¹ - - = f (x i , у , ), i = 0ДК , N -1 <        h                                             ,

  
  

• . У 0 = У a

Последовательные значения y _t определяется по формуле:

• Y+1 = Y + h * f (xi, y,)

Метод Эйлера имеет очень простую геометрическую

Искомая интегральная кривая y(x) на отрезке [a:b]

интерпретацию.

приближается к

ломанной, наклон которой на каждом элементарном участке определяется наклоном интегральной кривой уравнения в точке (х„у).

Приближенно можно считать, что правая часть

^ y = f ⁽ x , У )

^ x          , тогда

У , -+ 1 = У , - ^{+ д} У 1

,     У,+1 = У,+ h • f(xi- У I)

Применяя метод Эйлера к системе уравнений (9), получим р = V + (Pi-г X,+1     V xi +

<

V = V + ■(—i у ,+1       у , +

• ^-    X ai ) COS^{( a} , ) _м

mi

• ^-    X ai )sin^{( a} , ) ^- m i _д^

  m_i

  
  

Далее, используя зависимость (7), можем найти значение координат ЛА в каждый момент времени и построить график траектории движения ЛА при заданных начальных условиях

<

x i + 1

= Xj + VY - At i       xi

^ y_z -+ i = y i + V y -^A t

Метод Эйлера при достаточных малых величинах шага ^A t дает решение с большей точностью, так как погрешность ^{A t}  ^ 0 на каждом шаге расчета.

Программная реализация1    Блок-схема программы

По представленному численному методу была разработана блок-схема (рис.2)

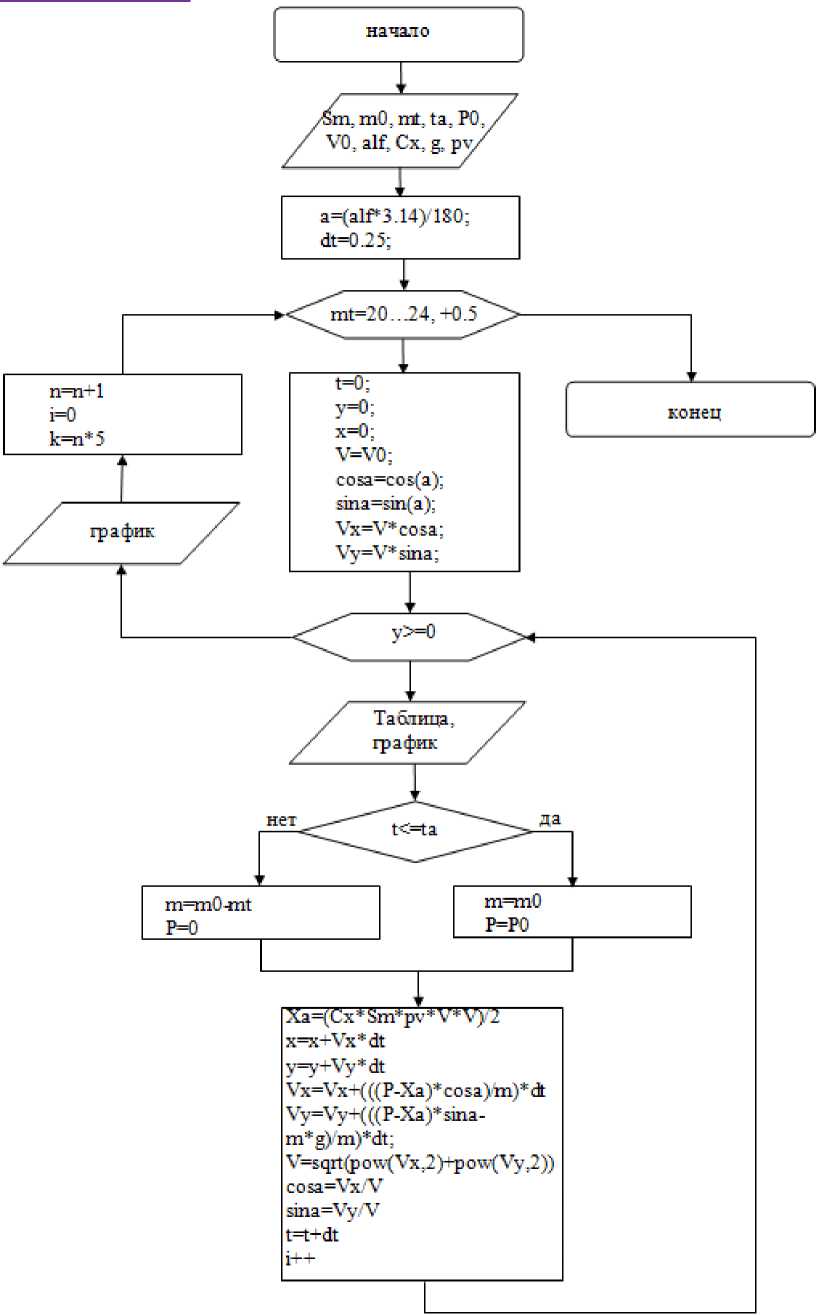
Рис.2 - Блок-схема программы

• 2    Описание программы

В ходе курсовой работы была разработана программа расчета траектории ЛА на языке CИ++.

Для удобства работы с программой сделаны несколько вкладок на одной форме: таблица координат (рис.3), траектории полета (рис.4), график зависимости дальности полета от массы топлива (рис.5).

Рис.3 - Таблица координат

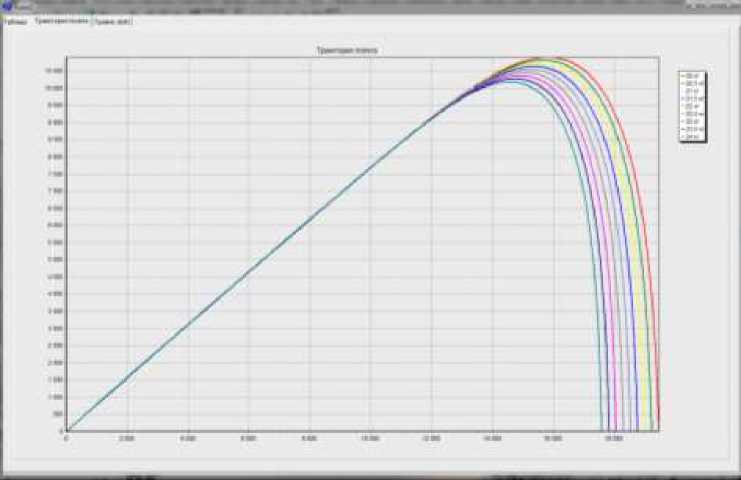
Рис.4 -

Траектория полета

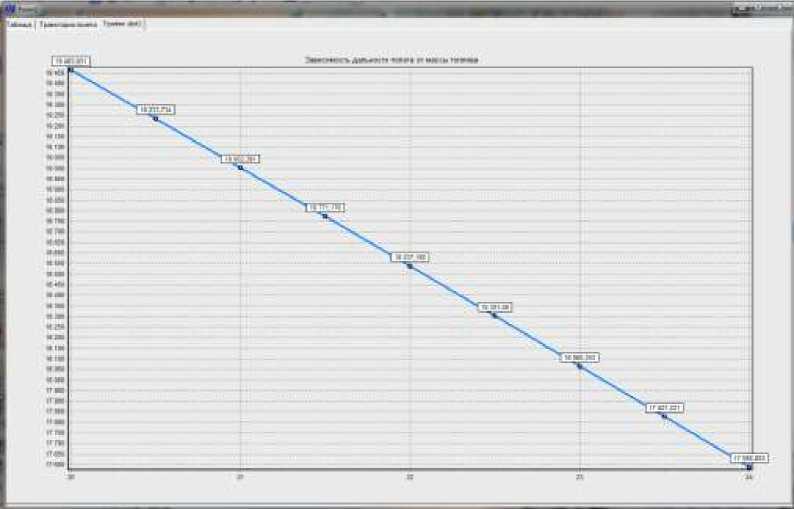
Рис.5 - График зависимости дальности полета от массы топлива

L Project! -bpr	25 04 2017 21:53	Семя -BPS’	4 КБ
I# Project! bpr Project! cpp	29 OS .2017 0:$?	6<6Proj#d
	25 04 7017 2i:$3	C * ♦ Bunder Source .	1 Кб
Ш Project! e«e	04 06 2017 10 21	Приложение	34 КБ
i Project! obj	0406.201710-20	6»*Л 'OBJ'	19 КБ
L Project! ret	2504.2017 21-46	0*мл RES'	1 КБ
. Project! tdi	04 06.2017 10 23	Саэйл IDS	2 368 КБ
	04   2017 10 21	Те<пок4Й дочм<п1	_____J
L Un	0306 2017 2210	Оийл -CPP*	3 КБ
Unrtl.-ddp	03 06 2017 2223	ОаАл -DOP	1 КБ
[ UMl-dfm	03X16.2017 22.23	Мл -DEM'	10 Кб
[ Un	0 3 06 2017 21:57	Мкл **Н"	г кб
Urwu .cpp	0306.2017 22110	С»-Bmfder Source...	1 • i
Unrtl.ddp	04 06 2017 037	Мл DOF	1 <ь
CW Un	03 06 2017 22:23	C**Buddff Form	10 КБ
[_ Undl .h	0306.2017 21:57	Смйл К	. В
, unei obj	0306.2017 2210	Ф»Ая OBJ"	153 Кб
[ Un«2obj	M.06 J017 10:15	Смйл OBJ"	36 КБ
Un«3 obj Рис.6	0406.2017 10:15	О»йл ОВГ	-

Текстовый файл с результатами

wt-20.oooooo «-н.меи* у-п.омгзо v-n^.иг7«я iM-20.OOOOOO «.«*.571501 у-71.0606*6 ¥»5»М0)М« mt-?o.oooooo «-хе». ?е,'еез y-iio.oonoi v-roo. )*»??i lM-20.OOOOOO «-154 2825 le У-Л1МЧИ V-1010. .'160)6 im-20. «10000 <-552.712410 y—iv. 779174 v-1221.457410 IM-20.000000 «..**2.»?76*1 y-626.1105*2 V-1420.754417 lift.20.000000 «-1072. 6344*1 y-«45.22)932 ¥.1605.316441 IM-20. OOOOOO 4-1368 977)61 y-10e2.196124 ¥-1771.0*4567 IM-20.OOOOOO 4-17)6 675056 y-1164.600461 ¥-1972.704)14 IM-20.000000 4-211*. 176204 y-1619.600194 ¥-20)1.047077 IM-20.000000 4-252 1.819361 y-19'4. 120876 ¥-2160.1544 21 IM-20. 000000 4-3951.981009 V-llO). 604456 ¥-2261.0*1666 IM-20.000000 4-3)99. 205740 y-2651,617116 ¥-3339.806100 IM-20.000000 4-3662. 2*5010 y-3006 9*1'10 ¥-2403.900545 IM-20 OOOOOO 4-4336. 3776’9 V-3F5, 761092 ¥-2455. 360376 IM-20.000000 4-4*24.939511 y-1’50.03146» V-2495.92116? IM-20.000000 4-5119.610694 y-4110.079157 ¥-2577.Mill? IM-20. OOOOOO 4-5*21.251269 y-4514.521746 ¥-2151.366020 IM-20.000000 4-6)27. 732541 y-4902,2 36015 ¥-2569. 382*19 IM-20.000000 4—66)6.083692 y-5292.29*766 ¥-2562.682663 IM-20. OOOOOO 4-7)51. 371961 y.5661 <№651 ¥-2592. 3)4696 IM-20.OOOOOO «-7*66.67)746 ¥-6076.76*592 ¥-2167.0201)5 mt-70.OOOOOO 4-879*. 094116 ¥-6404.712906 ¥-1669.171)97 im-20. OOOOOO 4-66'0. 17*66' ¥-66*7.224561 ¥-1647.4*66)1 im-20. OOOOOO «-«996. 771514 y-6915 «16201 ¥-1474.6)6691 IM-20.OOOOOO «-9291.045724 y-?l 57.965521 ¥-1116.179652 im-20. OOOOOO 4.9 5 59. 946 1 25 y-7)5*. *39064 ¥-1222.107522 lM-20.OOOOOO 4-9*04.354717 y-754 2.17240* ¥-1126.44 3*06 IM-20.OOOOOO 4-10029.925246 ¥-77)0.7*2613 ¥-1044,95)245 IM-20.000000 4-102)9.470626 ¥-7666.76)24 2 ¥-974.626)20 lM-20.OOOOOO 4-10435.2063.4 y-6011.«70396 ¥-911.261126 IM-20. OOOOOO 4-10616. 910455 y-«U 7.445616 V-»59. 20660.' IM-20.OOOOOO 4-10792.0)3697 y-*2'4,599514 ¥.«11,1*9662 lM-20.OOOOOO 4-10955,775612 y-«394.250611 ¥.766,255042 iM-20.OOOOOO «-Ш11.1405*3 ¥-*507.16776$ ¥-729. 5*1504 lM-20.OOOOOO 4-11256. 977)32 y-6614.001 500 ¥-604. 5897)# mr-20.OOOOOO 4-11400.011691 y-*715.106462 ¥-662.715*41 IM-20.OOOOOO 4-11)14 Л6’*) • y-6611.561 Hl ¥-611.614*09 IM-20.000000 —11664 0« ' 108 y-evO1. 1*0477 ¥-606.881297 IM-20.OOOOOO «-117*8,14)056 ¥-*990,52592» ¥-5*2.24 5956 iM-20 OOOOOO «-11907.4 505*4 y-90’3. 91574) ¥-559.46522* mt-20.OOOOOO «-12022.376996 ¥-9151.6)0**3 ¥-51*.1)2219

о»11<гм1»

Рис.7 - Текстовый файл с результатами

Анализ результатов расчетов

Данная программа позволяет проследить зависимость изменения дальности и времени полета от изменения массы топлива ( m = 20…24кг).

Дальность полета ЛА при изменении массы топлива с 20 до 24 кг меняется с до 19464м до 17589м. Как видно на рис.5, при увеличении массы топлива дальность полета ЛА значительно уменьшается. Это связано с тем, что у ЛА возрастает скорость в конце АУТ. В связи с тем, что у снаряда начинает увеличиваться скорость, то сопротивление тоже увеличивается, значит на ПУТ при большей массе топлива сопротивление будет больше, а скорость меньше. Следовательно, ЛА будет пролетать меньшее расстояние с массой топлива = 24 кг, нежели с массой топлива = 20кг.

Выводы

В данном исследовании была разработана численная модель, алгоритм и программа расчета неуправляемого полета ЛА на языке программирования СИ++ с заданными начальными условиями по известной математической модели. Так же было выполнено тестирование программы. Далее были проведены вычислительные эксперименты и анализ полученных результатов, построен график траекторий полета ЛА и график зависимости дальности полета от массы топлива.