Исследование влияния неопределённости фоновых показателей заболеваемости на прогноз радиационных рисков по моделям МКРЗ для российских популяций при однократном облучении

Текст научной статьи Исследование влияния неопределённости фоновых показателей заболеваемости на прогноз радиационных рисков по моделям МКРЗ для российских популяций при однократном облучении

Список литературы Исследование влияния неопределённости фоновых показателей заболеваемости на прогноз радиационных рисков по моделям МКРЗ для российских популяций при однократном облучении

Автор: Иванов В.К., Чекин С.Ю., Кащеев В.В., Максютов М.А., Корело А.М., Меняйло А.Н.

Журнал: Радиация и риск (Бюллетень Национального радиационно-эпидемиологического регистра) @radiation-and-risk

Статья в выпуске: 3 т.22, 2013 года.

Бесплатный доступ

Исследовано влияние неопределённости фоновых показателей заболеваемости и оценок параметров моделей МКРЗ на прогноз радиационных рисков для российских популяций при однократном облучении. Показано, что для российских популяций статистический разброс фоновых показателей заболеваемости солидными раками, при определении на основе 200 тыс. человеко-лет наблюдений, приводит к относительному увеличению среднего значения прогнозируемого риска до 1,6% и к относительному увеличению стандартного отклонения прогноза до 15,5%; при 500 тыс. человеко-лет наблюдений – к увеличению среднего значения прогнозируемого риска на 1% и стандартного отклонения прогноза на 6,6%. Статистическим разбросом фоновых показателей заболеваемости солидными раками, определённых на основе около 5 млн. человеко-лет наблюдений, при прогнозе радиационного риска можно пренебречь.

Еще

Радиационный риск, неопределённость оценок, однократное облучение

Короткий адрес: https://sciup.org/170170119

IDR: 170170119

Модели радиационных рисков, использованные в Рекомендациях МКРЗ 2007 г. [10] для обоснования системы радиологической защиты, можно применить для прогноза радиационных рисков в российских условиях с учётом характерных для России функции дожития и повозрастных показателей онкологической заболеваемости. При этом следует иметь в виду, что существенным источником занижения оценок радиационных рисков для российских популяций и когорт может быть недостаточно полная регистрация случаев онкозаболеваний и смертей в старших возрастных группах (старше 70-ти лет).

Помимо этого, оценкам радиационных рисков присущ фундаментальный статистический разброс в силу статистического разброса фоновых показателей заболеваемости и смертности, а также статистической неопределённости оценок параметров моделей радиационных рисков. Относительный вклад таких статистических разбросов в неопределённость оценки радиационного риска увеличивается, естественно, при уменьшении численности изучаемой когорты.

Совет по изучению радиационных эффектов при Национальной академии США в 2006 г. выпустил доклад БЭИР-7 [6], содержащий некоторый анализ неопределённостей оценки пожизненного радиационного риска. Для фактора эффективности дозы и мощности дозы (DDREF) взято среднее значение 1,5 со стандартным отклонением около 0,3, но дисперсия log(DDREF) затем увеличена в 1,5 раза, опираясь на экспертную оценку ([6], стр. 310). Поэтому самый большой вклад в дисперсию log(LAR) солидных раков внёс параметр DDREF: 74% для мужчин или 83% для женщин. По величине вклада в разброс риска солидных раков далее идёт разброс параметров моделей радиационных рисков (18% на логарифмической шкале риска для мужчин

Иванов В . К . – Председатель РНКРЗ , зам . директора по научн . работе , член - корр . РАМН ; Чекин С . Ю .* – ст . научн . сотр .; Кащеев В . В . – ст . научн . сотр ., к . б . н .; Максютов М . А . – зав . лаб ., к . т . н .; Корело А . М . – вед . программист ; Меняйло А . Н . – научн . сотр . ФГБУ МРНЦ Минздрава России .

или 11% для женщин) и вероятностное определение способа переноса риска с популяции на популяцию (8% или 6%, соответственно).

В представленной ниже работе исследовано влияние статистического разброса параметров моделей радиационных рисков и показателей онкологической заболеваемости на оценки параметров моделей радиационных рисков при однократном облучении, применительно к различным российским популяциям.

Материалы и методы

Модели МКРЗ-2007 [10] избыточного относительного риска ( ERR ) и избыточного абсолютного риска ( EAR ) для солидных раков выглядят следующим образом:

ERR D,g, и , s) = as ■ D- exp { - 0,017 ■ (g- 30) } ■

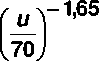
где s - индекс, обозначающий пол индивидуума ( s =м для мужского пола и s =ж для женского); а _м =0,35/Гр для мужчин и а _ж =0,58/Гр для женщин; и - текущий (достигнутый) возраст в годах; g - возраст на момент облучения в годах; D - поглощённая доза, Гр.

2,38

EAR (D,g, и ,s) = a_■ D-exp { -0,024■ (g-30) } - I Ц -1 , (2)

^s I 70 )

где а _м =432•10 " ⁵/Гр для мужчин и а _ж =598,3•10 " ⁵/Гр для женщин; остальные обозначения соответствуют (1).

Риск лейкозов даётся в виде модели избыточного абсолютного риска:

EAR(D, g,t,s) = as(g) ■ D(1 + 0,79 ■ D) ■ exp(ps (g) ■ (t- 25)),

где t - время, прошедшее после облучения, в годах (текущий возраст u=g+t ). Избыточный абсолютный риск EAR имеет размерность чел./год на 100 тыс. человек и зависит не только от возраста на момент облучения g , но и от времени t , прошедшего после облучения. Для лейкозов зависимость EAR от дозы D уже линейно-квадратичная. Латентный период для лейкозов принят равным 2 годам. В таблице 1 приведены значения параметров a_s и p_s модели (3) в зависимости от возраста при облучении g для мужчин и женщин.

Таблица 1

Значения параметров избыточного абсолютного риска EAR заболеваемости лейкозами

Возраст при облучении g , лет	Мужчины		Женщины
Возраст при облучении g , лет	а м , ЗВ	в м , год ^-1	а ж , Зв	в ж , год ^-1
0-19	3,3	-0,17	6,6	-0,07
20-39	4,8	-0,13	9,7	-0,03
> 39	13,1	-0,07	26,4	0,03

Рассмотрим модели солидных раков. Модели (1) и (2) имеют одну и ту же форму:

ER (D,g, и ,s) = as ■ D^ exp(a ■ g *) ■ (u * ^, (4)

где ER - избыточный риск, относительный или абсолютный, g =( g -30)/10 и и = и /70 - центрированные возраста в соответствии с (1) и (2), оценки параметров a_s , а, ю и их стандартные ошибки приведены ниже в таблице 2. Стандартные ошибки параметров в данном случае были приближённо рассчитаны из их доверительных интервалов, приведённых в [8] (стр. 15, таблица 10).

Таблица 2

Оценки параметров моделей избыточного относительного и абсолютного рисков и их стандартные ошибки , согласно [8], для солидных раков (4)

Модель	Пол, s	a s	Ст. ошибка a s	ω	Ст. ошибка ω	α	Ст. ошибка α
ERR	м	0,35	0,0457	-1,65	0,27439	-0,17	0,05488
ERR	ж	0,58	0,0793	-1,65	0,27439	-0,17	0,05488
EAR	м	432,0	67,07	2,38	0,27439	-0,24	0,04878
EAR	ж	598,3	54,88	2,38	0,27439	-0,24	0,04878

Таблица 3

Оценки параметров модели избыточного абсолютного риска EAR лейкозов (3) и их стандартные ошибки , согласно [7]

Возраст g , лет	Пол, s	а s	Ст. ошибка а s	β s	Ст. ошибка β s
0-19	м	3,3	0,56	-0,17	0
20-39	м	4,8	1,31	-0,13	0
> 39	м	13,1	2,63	-0,07	0
0-19	ж	6,6	1,30	-0,07	0
20-39	ж	9,7	1,92	-0,03	0
> 39	ж	26,4	5,15	0,03	0

Стандартные ошибки параметров модели лейкозов (3), приведённые в таблице 3, приближённо рассчитаны из таблицы числа избыточных радиационных лейкозов, приведённых в [7] (стр. 76, таблица V). Сведения для расчёта стандартной ошибки параметра β s в [7] отсутствуют.

При вычислении стандартных ошибок было сделано допущение, что оценки параметров – нормально распределённые случайные величины, так как были получены в [7] и [8] методом максимального правдоподобия (оценки максимального правдоподобия, ОМП, – асимптотически нормально распределены). Очевидно, что в силу нелинейности соотношения (4), распространение разброса параметров на величины ERR или EAR может быть оценено только с помощью имитационного моделирования.

В дальнейшем с помощью генератора независимо распределённых нормальных случайных величин было получено по 250 реализаций параметров а s , α , ω для 4-х вариантов модели (4) – для мужского и женского пола в вариантах ERR и EAR, т.е. 1000 реализаций моделей для прогноза избыточного радиационного риска. Приближение статистической независимости оценок параметров а s , α , ω , как показано в [9], для солидных раков является приемлемым.

Для модели лейкозов (3), поскольку единственным известным количественно источником статистического разброса является коэффициент удельного радиационного риска а s , все остальные члены формулы (3) образуют масштабный множитель. Поэтому для лейкозов в данном случае учёт разброса параметров модели является тривиальной задачей: чтобы получить стандартное отклонение погодового избыточного относительного риска, надо умножить стандартное отклонение коэффициента а s на D(1 + 0,79 ⋅ D) ⋅ exp( β s(g) ⋅ (t- 25)) . Например, максимальный избыточный абсолютный риск лейкозов у мужчин, облучённых в возрасте 30 лет дозой 0,1 Гр, достигается сразу после 2-летнего латентного периода и равен 10,9⋅10^-5/год при стандартном отклонении 2,98⋅10^-5/год. Данная тривиальная задача более подробно не рассматривается.

При моделировании процессов с использованием генератора случайных чисел в зависимости от рассматриваемой задачи необходим набор случайных величин, распредёленных по различным законам. Для получения случайных величин с заданным законом распределения или в необходимом интервале достаточно преобразовать заранее сгенерированные равномерно распределённые случайные числа из интервала (0; 1).

Для преобразования равномерного на интервале (0; 1) распределения в нормальное был использован метод Box-Muller [5], т.е. преобразование вида X = ( -J - 2ln U ⋅ sin(2 π V ) , где U и V – независимые равномерно распределённые на интервале (0; 1) случайные величины.

Оценка статистического разброса показателей заболеваемости проводилась в предположении пуассоновского процесса заболеваемости, т.е. при условии, что дисперсия абсолютного числа случаев заболеваний и число заболеваний равны.

Численные расчёты проводились с использованием медико-демографических данных популяций г. Обнинска, Людиново, Калужской области и России в целом (Приложения А и Б), а также данных онкозаболеваемости по России за 2001-2005 гг. [1-4].

Результаты и обсуждение

Из (4) следует, что при g =30 и u =70 ошибки коэффициентов α и ω не распространяются на EAR и ERR, т.е. для возраста при облучении 30 лет в возрасте 70 лет достигается минимум дисперсии прогнозируемого избыточного абсолютного риска (на логарифмической шкале).

Результаты учёта статистического разброса значений параметров моделей радиационных рисков

С учётом величины случайного разброса значений параметров а s , α , ω в (4), форма вероятностного распределения избыточного абсолютного риска солидных раков в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, согласно модели EAR (2), EAR(D=1 Гр, g=30 лет, u=70 лет), для мужчин и женщин, представлена на рис. 1 (для мужчин) и рис.2 (для женщин). Данные приведены по популяциям г. Обнинска, Людиново, Калужской области и России в целом. В ячейках таблиц под рисунками указаны частоты гистограмм в последовательных интервалах избыточного риска шириной по 50 на 100 тыс. чел.-лет. В качестве заголовков колонок используются правые точки среза интервалов гистограммы, например: на рис. 1, первая колонка – значения EAR от 275 до 325 на 100 тыс. чел.-лет, вторая колонка – значения EAR от 325 до 375 на 100 тыс. чел.-лет, и т.д.

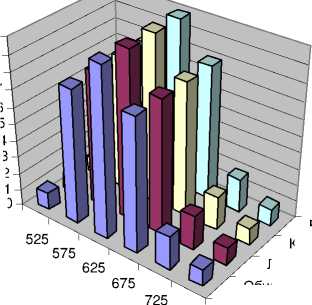
На рис. 3 и 4 приведены формы вероятностного распределения избыточного абсолютного риска солидных раков в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, согласно модели ERR (1), ERR(D=1 Гр, g=30 лет, u=70 лет), для мужчин и женщин. Данные приведены по популяциям г. Обнинска, Людиново, Калужской области и России в целом. Обозначения такие же, как на рис. 1 и 2. Для вычисления распределения избыточного абсолютного риска по модели ERR значение относительной величины ERR умножалось на значение фонового показателя заболеваемости солидными раками в возрасте 70 лет, по каждой из рассматриваемых популяций. Значения фоновых показателей на этом этапе анализа принимались детерминированными величинами, не имеющими статистического разброса.

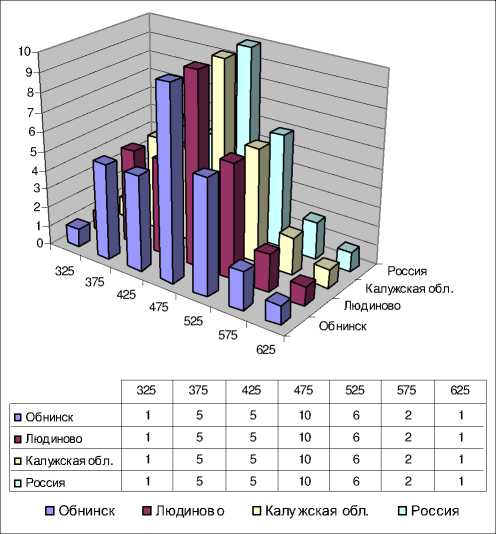
Рис . 1. Гистограмма вероятностного распределения избыточного абсолютного риска солидных раков (EAR⋅10⁵) в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, согласно модели EAR (2), EAR(D=1 Гр, g=30 лет, u=70 лет), для мужчин. Частоты гистограмм приведены в последовательных интервалах избыточного абсолютного риска шириной по 50 на 100 тыс. чел.-лет.

Обнинск

Россия

Калу жская обл.

Людинов о

□ Обнинск □ Людинов о □ Калу жская обл. □ Россия

Рис . 2. Гистограмма вероятностного распределения избыточного абсолютного риска солидных раков (EAR⋅10⁵) в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, согласно модели EAR (2), EAR(D=1 Гр, g=30 лет, u=70 лет), для женщин. Частоты гистограмм приведены в последовательных интервалах избыточного абсолютного риска шириной по 50 на 100 тыс. чел.-лет.

	425	475	525	575	625	675	725	775	825
□ Обнинск	1	0	6	6	8	5	2	2	0
□ Людиново	0	1	5	4	8	7	3	1	1
□ К алужск ая обл.	1	0	6	5	9	5	2	2	0
□ Россия	1	6	9	7	5	1	1	0	0

□ Обнинс к □ Людинов о □ Калу жская обл. □ Россия

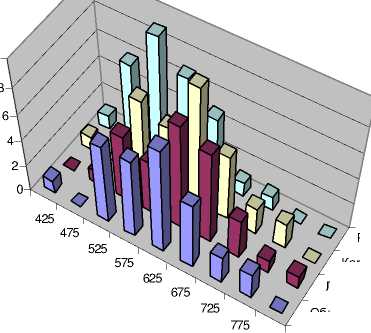
Россия

Калужская обл.

Людиново

Об нинск

Рис . 3. Гистограмма вероятностного распределения избыточного абсолютного риска солидных раков (EAR⋅10⁵) в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, согласно модели ERR (1), ERR(D=1 Гр, g=30 лет, u=70 лет), для мужчин. Частоты гистограмм приведены в последовательных интервалах избыточного абсолютного риска шириной по 50 на 100 тыс. чел.-лет.

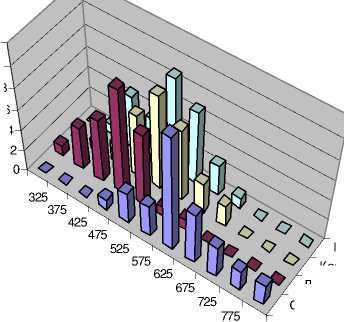
Обнинск

Россия

Калужская обл.

Людиново

	325	375	425	475	525	575	625	675	725	775	825
□ Обнинск	0	0	0	1	3	3	11	5	3	2	2
□ Людиново	1	4	6	10	7	1	1	0	0	0	0
□ К алужск ая обл.	0	1	2	6	9	7	3	2	0	0	0
□ Россия	0	1	5	4	9	7	3	1	0	0	0

□ Обнинск □ Людинов о □ Калу жская обл. □ Россия

Рис . 4. Гистограмма вероятностного распределения избыточного абсолютного риска солидных раков (EAR⋅10⁵) в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, согласно модели ERR (1), ERR(D=1 Гр, g=30 лет, u=70 лет), для женщин. Частоты гистограмм приведены в последовательных интервалах избыточного абсолютного риска шириной по 50 на 100 тыс. чел.-лет.

Как и следовало ожидать, распределение избыточного абсолютного риска, рассчитанного по модели EAR (2), одинаково для всех популяций, так как опирается только на модельные параметры. Распределение избыточного абсолютного риска, рассчитанного по модели ERR (1), различно для разных популяций, так как использует статистические данные о фоновых показателях заболеваемости солидными раками по каждой из популяций.

Формы всех четырёх распределений (рис. 1-4) достаточно симметричны, несмотря на относительные сдвиги наиболее вероятных значений риска для разных популяций в случае прогноза по модели избыточного риска ERR (1). Это позволяет достаточно полно охарактеризовать разброс значений избыточного абсолютного риска его дисперсией (или среднеквадратичным отклонением). В этом случае доверительные интервалы избыточного абсолютного риска также можно приближённо определить, считая распределение риска нормальным.

Вполне ожидаемым является факт, что в зависимости от возраста при облучении и достигнутого возраста соотношение между средними значениями избыточных абсолютных рисков солидных раков, прогнозируемых для российских популяций с помощью моделей EAR и ERR, могут значительно различаться. Это объясняется тем, что модели были идентифицированы на японской популяции, и на российской популяции их согласованность хуже.

Более важным и заранее неочевидным результатом проведённого имитационного моделирования является то, что, в зависимости от возраста при облучении и достигнутого возраста, соотношение между дисперсиями избыточных абсолютных рисков солидных раков, прогнозируемых с помощью моделей EAR и ERR, также могут значительно различаться.

Результаты учёта статистического разброса спонтанных показателей заболеваемости

Поскольку для лейкозов применяется одна аддитивная модель (EAR, ф-ла (3)), статистический разброс половозрастных показателей спонтанной заболеваемости лейкозами на оценке вероятности возникновения радиационно обусловленных лейкозов не сказывается, а проблема переноса риска между популяциями для лейкозов в настоящее время не формализована. Дальнейшее рассмотрение относится к солидным ракам.

На рис. 5-8 разброс прогнозируемого избыточного абсолютного риска солидных раков демонстрируется величиной 90% доверительных интервалов. Рис. 9 и 10 соответствуют риску в 70 лет при облучении в 30 лет, а рис. 7 и 8 – риску в 100 лет при облучении в 1 год. Так же, как и без учёта разброса спонтанных показателей заболеваемости, между этими двумя вариантами сохраняются существенные различия.

Рис. 5 и 6 (риск в возрасте 70 лет при облучении в возрасте 30 лет) показывают, что доверительные интервалы прогнозов риска по моделям EAR и ERR имеют приблизительно одинаковую величину, а средние значения прогнозов по этим разным моделям близки друг другу; наблюдается тенденция больших прогнозных значений избыточного абсолютного риска по моделям ERR, по сравнению с моделями EAR, для мужчин, и обратное соотношение – для женщин.

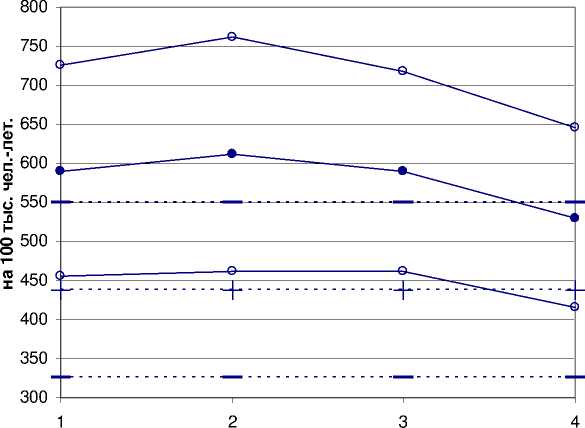
- - -+- - - Модель EAR — - — ^е — — - 90% ДИ —• Модель ERR —о 90% ДИ

Рис . 5. Мужчины. Избыточный абсолютный риск солидных раков в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, с 90% доверительными интервалами (90% ДИ), согласно моделям EAR и ERR, в четырёх популяциях (по горизонтали): 1 – г. Обнинск Калужской области, 2 – г. Людиново Калужской области, 3 – Калужская область, 4 – Россия. Разброс рисков обусловлен разбросом модельных параметров и статистическим разбросом фоновых показателей заболеваемости. Точки, соответствующие разным популяциям, соединены для наглядности демонстрации (практически одинаковой) ширины доверительных интервалов.

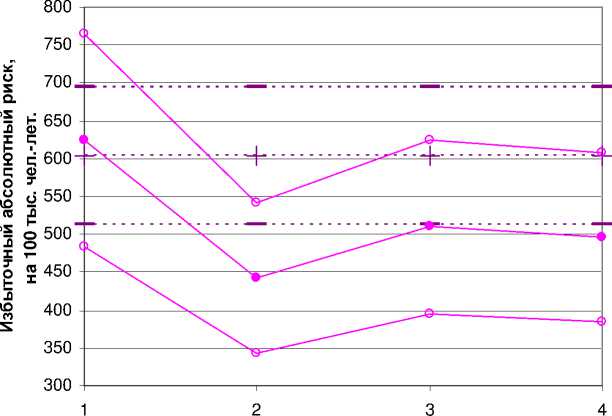
- --+-- - Модель EAR - - - ^е - - - 90% ДИ ---• Модель ERR ---© 90% ДИ

Рис . 6. Женщины. Избыточный абсолютный риск солидных раков в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, с 90% доверительными интервалами (90% ДИ), согласно моделям EAR и ERR, в четырёх популяциях (по горизонтали): 1 – г. Обнинск Калужской области, 2 – г. Людиново Калужской области, 3 – Калужская область, 4 – Россия. Разброс рисков обусловлен разбросом модельных параметров и статистическим разбросом фоновых показателей заболеваемости. Точки, соответствующие разным популяциям, соединены для наглядности демонстрации (практически одинаковой) ширины доверительных интервалов.

Таблица 4 даёт представление об увеличении разброса прогнозируемого согласно модели ERR избыточного абсолютного риска солидных раков в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет, при учёте разброса фоновых показателей, которыми характеризуется популяция. Относительный вклад от статистического разброса фоновых показателей в увеличение стандартного отклонения прогнозируемого риска не превышает 15,5% по всем рассмотренным популяциям. Это максимальное значение достигается для популяции г. Людиново, имеющей минимальную численность.

Однако, среднее значение прогнозируемого избыточного абсолютного риска при учёте разброса фоновых показателей также увеличивается из-за того, что фоновые показатели входят в прогнозируемый по модели ERR риск в виде сомножителя, т.е. вносимый ими разброс имеет мультипликативный характер. Из таблицы 5 видно, что относительное смещение (увеличение) среднего избыточного абсолютного риска за счёт разброса фоновых показателей достигает 1,5% (г. Людиново).

Таблица 4 Стандартное отклонение избыточного абсолютного риска ( на 100 тыс . чел ./ год ) солидных раков в достигнутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет , соглас но модели ERR, без учёта разброса фоновых показателей и с учётом разброса фоновых показателей

Пол	Популяция	Длит. периода сбора стат. данных, лет	Чел.-годы под наблюдением	Ст. откл. риска без учёта разброса фоновых показателей	Ст. откл. риска с учётом разброса фоновых показателей	Увеличение ст. откл., %
муж	г. Обнинск	5	243870	76,79	81,89	6,64
муж	г. Людиново	5	95785	79,07	91,29	15,46
муж	Калужская обл.	5	2413720	77,08	78,13	1,36
муж	Россия	2	133563024	69,54	69,65	0,16
жен	г. Обнинск	5	284265	85,54	90,79	6,14
жен	г. Людиново	5	113325	60,74	70,15	15,48
жен	Калужская обл.	5	2869520	69,92	70,80	1,26
жен	Россия	2	152553568	68,07	68,17	0,15

Таблица 5

Средний избыточный абсолютный риск ( на 100 тыс . чел ./ год ) солидных раков в достиг нутом возрасте 70 лет при облучении дозой 1 Гр в возрасте 30 лет , согласно модели ERR, без учёта разброса фоновых показателей и с учётом разброса фоновых показателей

Пол	Популяция	Длит. периода сбора стат. данных, лет	Чел.-годы под наблюдением	Изб. абс. риск х10 -5 /год без учёта разброса фоновых показателей	Изб абс. риск х10 -5 /год с учётом разброса фоновых показателей	Увеличение среднего значения риска, %
муж	г. Обнинск	5	243870	585,92	590,84	0,84
муж	г. Людиново	5	95785	603,31	612,09	1,45
муж	Калужская обл.	5	2413720	588,16	589,73	0,27
муж	Россия	2	133563024	530,64	530,85	0,04
жен	г. Обнинск	5	284265	623,69	628,90	0,83
жен	г. Людиново	5	113325	442,88	449,63	1,52
жен	Калужская обл.	5	2869520	509,83	511,18	0,26
жен	Россия	2	152553568	496,31	496,51	0,04

На рис. 7 и 8 (риск в возрасте 100 лет при облучении в возрасте 1 год) доверительные интервалы прогнозов риска по модели EAR существенно шире, чем для прогнозов по модели ERR. Как для мужчин, так и для женщин средние значения прогнозов по модели EAR в разы выше, чем по модели ERR (p<0,001), а различия прогноза между популяциями пренебрежимо малы по сравнению с различиями прогноза по разным моделям.

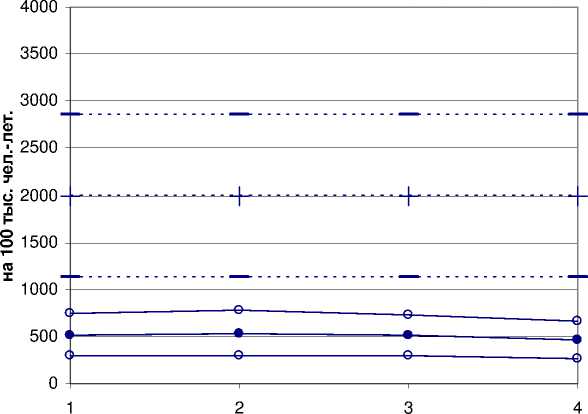
- - -+- - - Модель EAR — - — ^™ - — - 90% ДИ —• Модель ERR 9 90% ДИ

Рис . 7. Мужчины. Избыточный абсолютный риск солидных раков в достигнутом возрасте 100 лет при облучении дозой 1 Гр в возрасте 1 год, с 90% доверительными интервалами (90% ДИ), согласно моделям EAR и ERR, в четырёх популяциях (по горизонтали): 1 – г. Обнинск Калужской области, 2 – г. Людиново Калужской области, 3 – Калужская область, 4 – Россия. Разброс рисков обусловлен разбросом модельных параметров и статистическим разбросом фоновых показателей заболеваемости. Точки, соответствующие разным популяциям, соединены для наглядности демонстрации ширины доверительных интервалов.

- --+-- - Модель EAR - - - ^е - - - 90% ДИ ---• Модель ERR ---9 90% ДИ

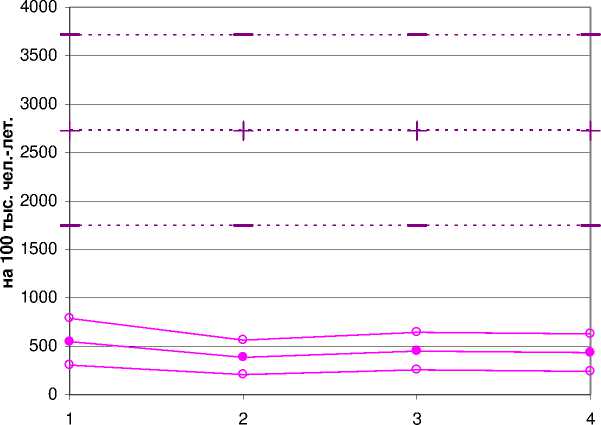
Рис . 8. Женщины. Избыточный абсолютный риск солидных раков в достигнутом возрасте 100 лет при облучении дозой 1 Гр в возрасте 1 год, с 90% доверительными интервалами (90% ДИ), согласно моделям EAR и ERR, в четырёх популяциях (по горизонтали): 1 – г. Обнинск Калужской области, 2 – г. Людиново Калужской области, 3 – Калужская область, 4 – Россия. Разброс рисков обусловлен разбросом модельных параметров и статистическим разбросом фоновых показателей заболеваемости. Точки, соответствующие разным популяциям, соединены для наглядности демонстрации ширины доверительных интервалов.

В таблице 6 приведено увеличение разброса прогнозируемого согласно модели ERR избыточного абсолютного риска солидных раков в достигнутом возрасте 100 лет при облучении дозой 1 Гр в возрасте 1 год, при учёте разброса фоновых показателей, которыми характеризуется популяция. Относительный вклад от статистического разброса фоновых показателей в увеличение стандартного отклонения прогнозируемого риска для данной комбинации возрастов (1 год при облучении и 100 лет достигнутого возраста) не превышает 6,3% (г. Людиново) по всем рассмотренным популяциям. Из таблицы 7 видно, что относительное смещение (увеличение) среднего избыточного абсолютного риска за счёт разброса фоновых показателей достигает 1,65% (г. Людиново).

Таблица 6 Стандартное отклонение избыточного абсолютного риска ( на 100 тыс . чел ./ год ) солидных раков в достигнутом возрасте 100 лет при облучении дозой 1 Гр в возрасте 1 год , соглас но модели ERR, без учёта разброса фоновых показателей и с учётом разброса фоновых показателей

Пол	Популяция	Длит. периода сбора стат. данных, лет	Чел.-годы под наблюдением	Ст. откл. риска без учёта разброса фоновых показателей	Ст. откл. риска с учётом разброса фоновых показателей	Увеличение ст. откл., %
муж	г. Обнинск	5	243870	132,39	136,03	2,75
муж	г. Людиново	5	95785	136,31	144,55	6,04
муж	Калужская обл.	5	2413720	132,89	133,75	0,65
муж	Россия	2	133563024	119,89	120,00	0,08
жен	г. Обнинск	5	284265	143,20	147,00	2,65
жен	г. Людиново	5	113325	101,68	108,09	6,30
жен	Калужская обл.	5	2869520	117,06	117,78	0,62
жен	Россия	2	152553568	113,95	114,04	0,08

Таблица 7

Средний избыточный абсолютный риск ( на 100 тыс . чел ./ год ) солидных раков в достиг нутом возрасте 100 лет при облучении дозой 1 Гр в возрасте 1 год , согласно модели ERR, без учёта разброса фоновых показателей и с учётом разброса фоновых показателей

Пол	Популяция	Длит. периода сбора стат. данных, лет	Чел.-годы под наблюдением	Изб. абс. риск х10 -5 /год без учёта разброса фоновых показателей	Изб абс. риск х10 -5 /год с учётом разброса фоновых показателей	Увеличение среднего значения риска, %
муж	г. Обнинск	5	243870	513,85	518,51	0,91
муж	г. Людиново	5	95785	529,10	537,42	1,57
муж	Калужская обл.	5	2413720	515,81	517,30	0,29
муж	Россия	2	133563024	465,36	465,57	0,04
жен	г. Обнинск	5	284265	547,19	552,13	0,90
жен	г. Людиново	5	113325	388,56	394,96	1,65
жен	Калужская обл.	5	2869520	447,30	448,57	0,28
жен	Россия	2	152553568	435,44	435,62	0,04

Выводы

Таким образом, в ситуации однократного острого облучения:

o Статистический разброс фоновых показателей заболеваемости солидными раками, определённых на основе около 200 тыс. человеко-лет наблюдений (г. Людиново, 5 лет наблюдений), приводит к относительному увеличению среднего значения прогнози- руемого риска до 1,6% и к относительному увеличению стандартного отклонения прогноза до 15,5%.

о Статистический разброс фоновых показателей заболеваемости солидными раками, определённых на основе около 500 тыс. человеко-лет наблюдений (г. Обнинск, 5 лет наблюдений), приводит к относительному увеличению среднего значения прогнозируемого риска до 1% и к относительному увеличению стандартного отклонения прогноза до 6,6%.

o Статистическим разбросом фоновых показателей заболеваемости солидными раками, определённых на основе около 5 млн. человеко-лет наблюдений (Калужская область, 5 лет наблюдений), при прогнозе радиационного риска можно пренебречь.

Приложение А

Повозрастные показатели заболеваемости злокачественными новообразованиями за период 2001-2005 гг. в г. Обнинске, г. Людиново, Калужской области, России

Таблица А.1

Повозрастные показатели заболеваемости ( на 100 тыс . чел .- лет ) всеми злокачественны ми новообразованиями ( код МКБ -10: C00- С 97) за период 2001-2005 гг . ( мужчины )

Возраст на момент диагноза, лет	Административная территория
Возраст на момент диагноза, лет	г. Обнинск	г. Людиново	Калужская область	Россия*
0-14	20,9	5,5	12,5	11,3
15-19	16,4	0	17,5	15,6
20-24	39,5	26,8	24	21,2
25-29	46,8	40,6	34,3	23,9
30-34	59,7	0	43,3	34,4
35-39	76,8	42,5	53,8	53,5
40-44	127,6	161,7	113,9	104,7
45-49	217,3	264,9	277	234,2
50-54	445	749	548	477,1
55-59	854,1	1105,4	1075,7	1121,8
60 и более	1735	1757,5	1724,8	1548,1
Итого	394,5	370,6	404,7	328,3

* Для вычислений использованы данные по России за 2001-2005 гг. [1-4].

Таблица А.2

Повозрастные показатели заболеваемости ( на 100 тыс . чел .- лет ) злокачественными новообразованиями лимфоидной , кроветворной и родственных им тканей

( код МКБ -10: C81-C96) за период 2001-2005 гг . ( мужчины )

Возраст на момент диагноза, лет	Административ ная территория
Возраст на момент диагноза, лет	г. Обнинск	г. Людиново	Калужская область	Россия*
0-14	7,8	5,5	5,2	5,3
15-19	8,2	0	10,1	6,6
20-24	4,9	13,4	9,4	7,4
25-29	17,6	27,1	9,7	7
30-34	23,9	0	9,1	6,8
35-39	10,2	0	7,3	7,4
40-44	13,2	21,6	9,4	9
45-49	21,2	11	15,3	14,1
50-54	36,6	13,9	21,2	21,9
55-59	46,9	34,5	42,9	44,6
60 и более	82,3	55,7	65,7	51,3
Итого	26,7	16,7	20,2	16

* Для вычислений использованы данные по России за 2001-2005 гг. [1-4].

Таблица А.3

Повозрастные показатели заболеваемости ( на 100 тыс . чел .- лет ) всеми злокачественны ми новообразованиями ( код МКБ -10: C00- С 97) за период 2001-2005 гг . ( женщины )

Возраст на момент диагноза, лет	Административная территория
Возраст на момент диагноза, лет	г. Обнинск	г. Людиново	Калужская область	Россия*
0-14	13,9	18	11,3	10
15-19	12,5	12,3	17,1	13,8
20-24	25	25,4	28	24,5
25-29	85,7	53,4	47,1	43,7
30-34	53,8	86,4	82,8	77,5
35-39	168,6	118	116,5	111,4
40-44	232	305,3	207,6	182,6
45-49	379,3	300,3	336	315,6
50-54	560,8	549,1	459	452,7
55-59	860,6	954,8	764,1	845
60 и более	1121	784,2	905,4	878,3
Итого	405,6	329,1	367	326,9

* Для вычислений использованы данные по России за 2001-2005 гг. [1-4].

Таблица А.4

Повозрастные показатели заболеваемости ( на 100 000 чел .- лет ) злокачественными ново образованиями лимфоидной , кроветворной и родственных им тканей

( код МКБ -10: C81-C96) за период 2001-2005 гг . ( женщины )

Возраст на момент диагноза, лет	Административная территория
Возраст на момент диагноза, лет	г. Обнинск	г. Людиново	Калужская область	Россия*
0-14	5,6	12	4,5	4,2
15-19	4,2	12,3	3,2	5,5
20-24	5	12,7	9	7,3
25-29	5,7	26,7	8	7,4
30-34	10,8	28,8	10,6	7,8
35-39	22,8	0	8	6,9
40-44	15,2	19,1	10,7	7,4
45-49	17,4	30	9,5	11,2
50-54	23	12,2	18,8	16,6
55-59	29,4	0	23,4	31,8
60 и более	60	30,8	38,1	34
Итого	23,2	19,4	17,1	14,8

* Для вычислений использованы данные по России за 2001-2005 гг. [1-4].

Приложение Б

Численность населения в различных возрастных группах в г. Обнинске, г. Людиново, Калужской области, России

(по данным переписи населения 2002 года)

Таблица Б.1

Таблица Б.2

Численность жителей г . Обнинска по данным переписи 2002 года

Возраст, лет	Мужчины	Женщины	Оба пола
0-14	7656	7190	14846
15-19	4883	4816	9699
20-24	4050	3997	8047
25-29	3416	3501	6917
30-34	3348	3717	7065
35-39	3907	4389	8296
40-44	4547	5258	9805
45-49	3774	4587	8361
50-54	3281	4351	7632
55-59	2131	2719	4850
60 и более	7781	12328	20109
Итого	48774	56853	105627

Численность жителей г . Людиново по данным переписи 2002 года

Возраст, лет	Мужчины	Женщины	Оба пола
0-14	3632	3337	6969
15-19	1646	1630	3276
20-24	1495	1575	3070
25-29	1477	1498	2975
30-34	1291	1389	2680
35-39	1413	1525	2938
40-44	1855	2096	3951
45-49	1812	1998	3810
50-54	1442	1639	3081
55-59	579	775	1354
60 и более	2515	5203	7718
Итого	19157	22665	41822

Таблица Б.3

Численность жителей Калужской области по данным переписи 2002 года

Возраст, лет	Мужчины	Женщины	Оба пола
0-14	80059	76001	156060
15-19	43437	43164	86601
20-24	38389	37828	76217
25-29	34972	34791	69763
30-34	32830	33819	66649
35-39	35658	37604	73262
40-44	44795	48653	93448
45-49	41953	46375	88328
50-54	35767	41570	77337
55-59	18202	23033	41235
60 и более	76682	151066	227748
Итого	482744	573904	1056648

Таблица Б.4

Численность жителей России по данным переписи 2002 года

Возраст, лет	Мужчины	Женщины	Оба пола
0-14	11859113	11274911	23134024
15-19	6275111	6073426	12348537
20-24	5598784	5504938	11103722
25-29	5243556	5195218	10438774
30-34	4994225	4744694	9738919
35-39	4952094	5039220	9991314
40-44	6037332	6352408	12389740
45-49	5589465	6155935	11745400
50-54	4690817	5481095	10171912
55-59	2422708	3039256	5461964
60 и более	9118307	17415683	26533990
Итого	66781512	76276784	1.43E+08

□ Людиново

□ К алужск ая обл.

Злокачественные новообразования в России в 2001 году (заболеваемость и смертность)/под ред. В.И.Чиссова, В.В.Старинского, Г.В.Петровой. М.: МНИОИ им. П.А. Герцена, 2003. 240 с.
Злокачественные новообразования в России в 2002 году (заболеваемость и смертность)/под ред. В.И.Чиссова, В.В.Старинского, Г.В.Петровой. М.: МНИОИ им. П.А. Герцена, 2004. 256 с.
Злокачественные новообразования в России в 2004 году (заболеваемость и смертность)/под ред. В.И.Чиссова, В.В.Старинского, Г.В.Петровой. М.: ФГУ МНИОИ им. П.А. Герцена, 2006. 248 с.
Злокачественные новообразования в России в 2005 году (заболеваемость и смертность)/под ред. В.И.Чиссова, В.В.Старинского, Г.В.Петровой. М.: ФГУ МНИОИ им. П.А. Герцена, 2007. 252 с.
Box G.E.P., Muller M.E. A Note on the Generation of Random Normal Deviates//The Annals of Mathematical Statistics. 1958. V. 29, N. 2. P. 610-611.
National Research Council, Committee on the Biological Effects of Ionizing Radiations (BEIR VII PHASE 2), Health risks from exposure to low levels of ionizing radiation. Washington, DC: Natl Acad. Press, 2006.
Preston D.L., Kusumi S., Tomonaga M., Izumi S., Ron E., Kuramoto A., Kamada N., Dohy H., Matsuo T., Nonaka H., Thompson D.E., Soda M., Mabuchi K. Cancer incidence in atomic bomb survivors. Part III: Leukemia, lymphoma and multiple myeloma, 1950-1987//Radiation Research. 1994. V. 137S. P. 68-97.
Preston D.L., Ron E., Tokuoka S. et al. Solid cancer incidence in atomic bomb survivors: 1958-1998//Radiation Research. 2007. V. 168. P. 1-64.
Report of the NCI-CDC working group to revise the 1985 NIH Radioepidemiological Tables. National Cancer Institute, National Institute of Health. NIH publication No. 03-5387, 2003. 118 p.
The 2007 Recommendations of the International Commission on Radiological Protection. ICRP Publication 103//Annals of the ICRP. 2007. V. 37, N 2-4. Elsevier, 2007. 332 p.

Еще

Статья научная