Исследование влияния первоначальных радиальных деформаций на распределение остаточных напряжений в поверхностно упрочнённом цилиндре

Вакулюк Владимир Степанович кандидат технических наук, доцент, кафедра сопротивления материалов.

Михалкина Светлана Алексеевна, старший преподаватель, кафедра высшей математики.

Сургутанов Николай Андреевич, аспирант, кафедра сопротивления материалов.

Кочерова Евгения Евгеньевна, соискатель, кафедра сопротивления материалов.

пользовании уравнений теории упругости, записанных в цилиндрической системе координат

,(1)

,(2)

,(3)

где         – радиальные, окружные и осевые остаточные напряжения;

– радиальные, окружные и осевые первоначальные деформации; – модуль продольной упругости материала; – коэффициент Пуассона.

Для расчёта методом конечно-элементного моделирования рассмотрен сплошной цилиндр, эскиз которого приведен на рис. 1.

В кольцевом поверхностном слое цилиндра толщиной 8 = b - c возникли, в силу различных причин, остаточные первоначальные деформации              Расчёты выполнены для сле дующих вариантов сочетания компонент первоначальных деформаций:

• 1)      =            =    (вариант 1);

• 2)      = -   ;     =    = (вариант 2);

• 3)      = -2 ;     =    = (вариант 3).

Варианты 1 и 3 рассмотрены в работе Биргера И.А. [1], вариант 2 изучается для сравнения. Для расчёта были приняты следующие численные значения параметров: b = 5мм; c = 4,5мм; E = 200000 МПа; μ = 0,3;   = 0,001.

Для решения задачи МКЭ был использован расчётный комплекс PATRAN /NASTRAN. Ко-

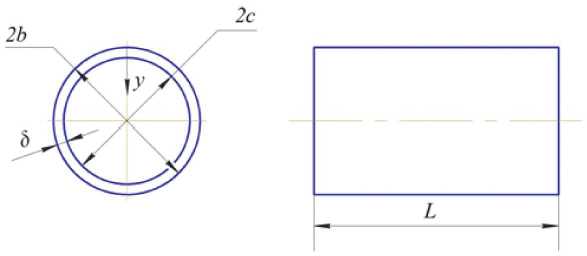
Рис. 1. Эскиз цилиндра с первоначальными деформациями поверхностного слоя

нечно-элементная модель в осесимметричной постановке представляла собой четверть сечения цилиндра с наложением соответствующих граничных условий. Принятая длина расчётной области цилиндра исключала влияние краевых зон для сечения, в котором значения компонент остаточных напряжений сравнивались с их значениями при аналитическим решении. При моделировании был использован треугольный шестиузловой осесимметричный конечный элемент типа 2D-Solid.

Первоначальная деформация £q = 0,001 в поверхностном слое моделировалась как температурное расширение тела с использованием ортотропного материала. При этом коэффициент ли нейного расширения СЕ = 0,00001 принимался град в окружном и осевом направлениях системы координат постоянным для всех расчётных случаев, а в радиальном направлении принималась ве- личина СЕ, которая обеспечивает заданные в со- ответствии с изучаемым вариантом значения £0г . Перепад температуры поверхностного слоя цилиндра относительно внутренней области принимался дг = 100°C .

Результаты расчёта распределения остаточных напряжений по толщине поперечного сечения цилиндра в виде графиков приведены на рис. 2 – 4. На графиках отсчёт оси y выполняется от поверхности к оси цилиндра (рис. 1).

Из приведённых на рис. 2 – 4 распределений остаточных напряжений следует, что при смене знака и увеличении по абсолютной величине первоначальной радиальной деформации радиальные остаточные напряжения сг повышаются в поверхностном слое и внутренней полости цилиндра. Сжимающие окружные Уд и осевые а_в остаточные напряжения в поверхностном слое также возрастают. При этом первоначальные радиальные деформации наибольшее влияние

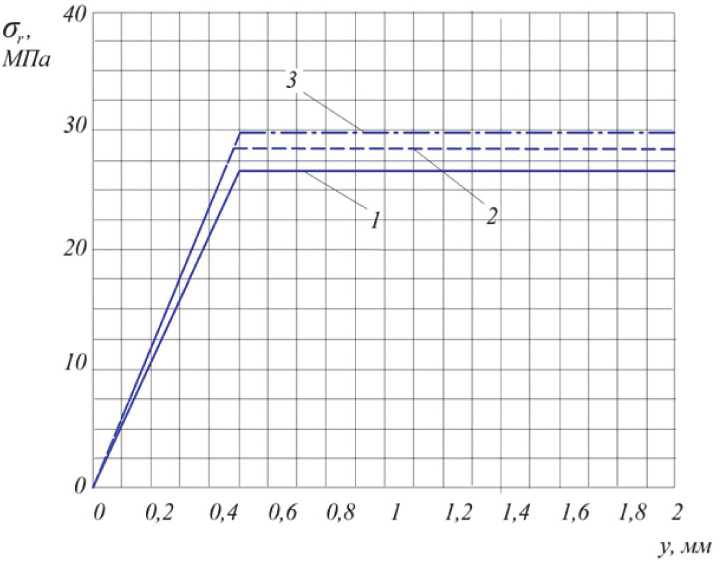
Рис. 2. Распределение радиальных У_г остаточных напряжений в поперечном сечении цилиндра (номера графиков соответствуют вариантам распределения первоначальных деформаций)

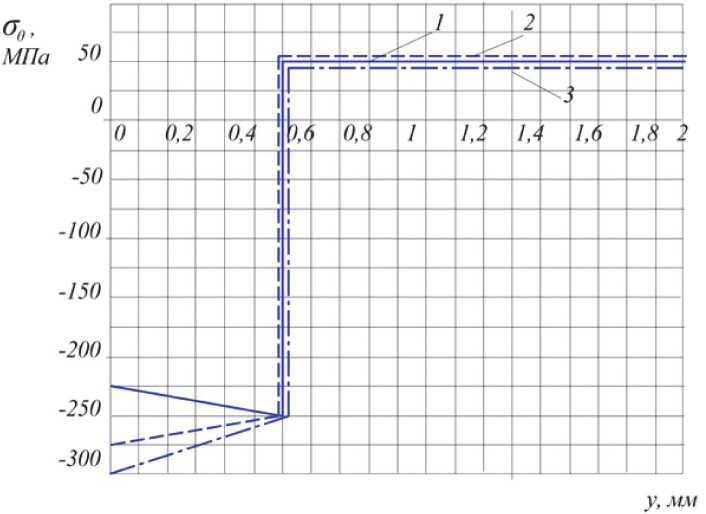
Рис. 3. Распределение окружных £jg остаточных напряжений в поперечном сечении цилиндра

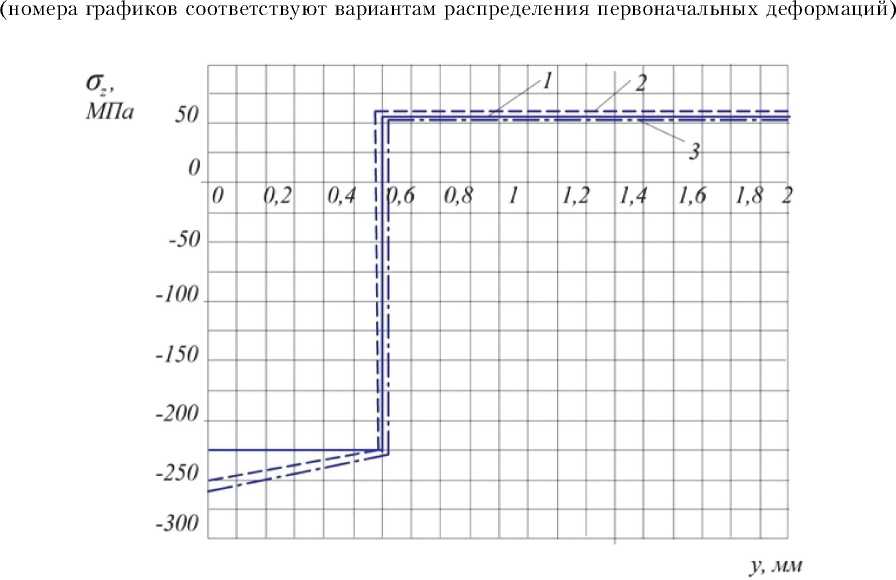
Рис. 4. Распределение осевых tJ остаточных напряжений в поперечном сечении цилиндра (номера графиков соответствуют вариантам распределения первоначальных деформаций)

оказывают на окружные сжимающие остаточные напряжения, действующие на поверхности цилиндра (рис. 3).

Следует обратить внимание на то, что при различных вариантах сочетания компонент первоначальных деформаций растягивающие (реактивные) окружные tJg и осевые £7 (рис. 3 и 4) остаточные напряжения постоянны в поперечном сечении цилиндра, на что указывалось в работе

• [2]. Эта закономерность позволяет считать реактивные остаточные напряжения постоянными при их экспериментальном определении, исходя из уравнений равновесия.

Установлено, что приращение предела выносливости поверхностно упрочнённой детали, в основном, определяется сжимающими остаточными напряжениями, возникающими в тонком поверхностном слое. При прогнозировании при- ращения предела выносливости детали APr (До^ДТд) за счёт поверхностного упрочнения наиболее оправдано использование критерия среднеинтегральных остаточных напряжений ст [4–6]. В этом случае величина АР„ оп-

ОСЖ 1 J                                   А ределяется по следующей формуле:

APr = ^Р • l"_OfJ ,         (4)

где V'p(^V't) – коэффициент влияния поверхностного упрочнения по критерию среднеинтегральных остаточных напряжений ^ост ,

СТост — " /0 J^Z^ ^' (5) где ^(О – осевые остаточные напряжения в опасном сечении детали по толщине поверхностного слоя уЛ = y/t^ – расстояние от поверхности детали до текущего слоя, выраженное в долях ^^^ , ^6р – критическая глубина нераспро-страняющейся трещины усталости, возникающей в упрочнённой детали при работе на преде- ле выносливости.

Необходимые для расчёта приращения предела выносливости по формуле (4) поверхностно упрочнённой детали значения коэффициента влияния Ч’р и критической глубины нерасп-ространяющейся трещины усталости ^кр можно вычислить по методикам, изложенным в работах [5, 7]. При определении критерия среднеинтегральных остаточных напряжений ст использовалось аналитическое решение задачи теории упругости о перераспределении остаточных напряжений гладкой детали при нанесении на неё надреза полуэллиптического профиля [8]. Из формулы (5) следует, что критерий ст зависит только от осевых ^(О остаточных напряжений поверхностного слоя упрочнённой детали. На основании анализа распределения осевых остаточных напряжений, приведённых на рис. 4, видно, что переход от изотропного распределения первоначальных деформаций (вариант 1) к анизотропному (вариант 2 и 3) незначительно изменяет значения осевых сжимающих остаточных напряжений, особенно при удалении от поверхности к оси детали. В соответствии с формулой (5) критерий ст , учитывающий характер распределения осевых остаточных напряжений по толщине поверхностного слоя упрочнённой детали, будет изменяться ещё меньше. В связи с этим, из анализа данных рис. 4 и формулы (4) можно сделать вывод, что расчёт остаточных напряжений по варианту изотропных первоначальных деформаций (вариант 1) является расчётом в запас прочности упрочнённой детали.

ВЫВОДЫ

• 1.    С увеличением по абсолютной величине радиальной первоначальной деформации увеличиваются по абсолютной величине все компоненты остаточного напряжённого состояния: радиальные, окружные и осевые остаточные напряжения .

• 2.    Растягивающие (реактивные) окружные и осевые остаточные напряжения постоянны в поперечном сечении детали.

• 3.    Расчёт остаточных напряжений по изотропным первоначальным деформациям является расчётом в запас прочности упрочнённой детали.