Исследование влияния структуры подвеса инерционной массы стеклянного микромеханического акселерометра на его характеристики

распространяется под лицензией CC BY 4.0. Чтобы просмотреть копию этой лицензии, посетите

Разработка новых конструктивных схем и применяемых материалов для производства МЭМС датчиков является актуальной задачей. В частности, микромеханические акселерометры (ММА) имеют широкий спектр применения в различных технических устройствах [1, 2]. Их широкое распространение обусловлено относительно невысокой стоимостью производства, малыми габаритами и массой, низким энергопотреблением.

ММА предназначены для измерения проекции линейного ускорения на ось чувствительности.

Одной из разновидностей конструктивных схем такого датчика является ММА маятникового типа. Чувствительным элементом такого прибора является физический маятник [1–3]. При воздействии на маятник составляющей линейного ускорения в направлении измерительной оси прибора маятник отклоняется относительно корпуса. Это отклонение фиксируется емкостным датчиком и передается в измерительную схему прибора.

Данная работа является продолжением исследований авторов по разработке возможных конструктивных схем акселерометра из радиостойкого стекла [4, 5] и перспектив по его применению.

В работе решаются следующие задачи:

• -    разработка конструктивной схемы маятникового акселерометра из радиостойкого стекла марки К108, удовлетворяющей требованиям по допустимым напряжениям в материале прибора, собственным частотам, обеспечению достаточной чувствительности при измерении ускорений до 50g с подвесом инерционной массы (ИМ) из стеклянных трубок круглой и гексагональной формы;

• -    расчет и сравнительная оценка механических характеристик ММА с разными подвесами ИМ;

• -    расчет параметров предполагаемого емкостного датчика при различных значениях ускорения.

1.    Конструкция акселерометра

Исходный прототип ММА, изображенный на рис. 1, представляет собой ММА маятникового типа, выполненный из стеклянных стержней методом вытягивания под воздействием высокой температуры. ИМ и подвес сформированы путем химического травления растворимого стекла.

1m

Рис. 1. Прототип стеклянного ММА

В предыдущих работах [4, 5] расчеты механических свойств прототипа были сделаны с осью чувствительности, размещенной перпендикулярно плоскости ММА. В такой конфигурации полученные результаты не позволяют говорить о возможности применить прототип на практике в силу недостаточной чувствительности, так как в этом случае предполагаемый емкостной датчик работает по принципу изменяемой площади пластин конденсатора, сформированных на боковых гранях ИМ и основания, и при малых перемещениях ИМ масштабный коэффициент очень мал для регистрации ускорения.

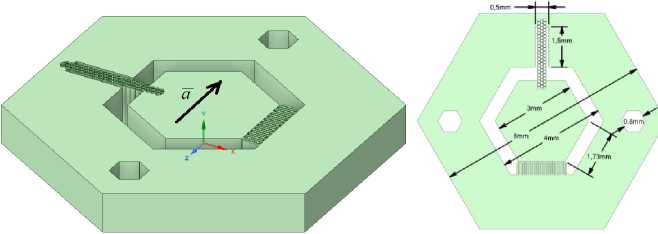
В настоящей работе предложена альтернативная конструктивная схема. Особенности предложенной схемы состоят, во-первых, в том, что для обеспечения достаточного отклонения ИМ для регистрации ускорения структура подвеса ИМ должна быть сформирована из стеклянных трубок вместо стержней. Во-вторых, для реализации емкостного датчика для съема полезного сигнала предлагается сформировать гребенку на одной грани ИМ и соседней грани основания с интегрированной или напыленной на ее поверхности токопроводящей пластины. Предлагаемая схема и общий вид представлены на рис. 2.

а)                                         б)

0.35 мм

в)

Рис. 2. Общий вид (а), размеры (б) и фрагмент гребенки с размерами (в)

При выбранных размерах ИМ и пластин гребенки возможно сформировать 12 гребенок, образующих емкостной датчик перемещений.

В представленной конструкции ММА подвес длиной 2 мм представляет собой структуру из трех рядов спаянных между собой стеклянных трубок круглой или гексагональной формы, размером 125 мкм и толщиной стенки 10–20 мкм, что должно обеспечить достаточную упругость подвеса. В данной работе толщина стенки трубок, составляющих подвес ИМ, принята равной 20 мкм. Толщина датчика – 1 мм. Общая масса модели составляет приблизительно 0.12 г, а масса ИМ – 0.02 г.

Вся конструкция ММА выполняется путем вытяжки преформы, набранной из стеклянных трубок и штабиков. На рис. 3 показаны два примера, получаемых после перетяжки структур из стеклянных трубок без откачки воздуха и с откачкой.

а)

Рис. 3. Структуры, получающиеся после совместной перетяжки сборки из тонкостенных трубок; а) без откачки воздуха; б) с откачкой воздуха

б)

В первом случае (рис. 3а) спекание происходит по линии соприкосновения трубок в пакете. Форма трубок остается близкой к круглой, между трубками образуются треугольные зазоры. Во втором случае зазоры между элементами отсутствуют, при этом форма трубок получается гексагональной. Для получения структур без воздушных зазоров между элементами используется вакуумирование при перетяжке. Структура, собранная из отдельных элементов, помещается в трубку большого диаметра (оболочку). При подаче преформы в печь, верхний конец трубки подключается через переходник к вакуумному насосу и в течение процесса поддерживается давление 0.2–0.3 атм.

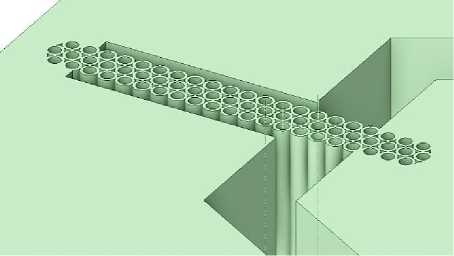
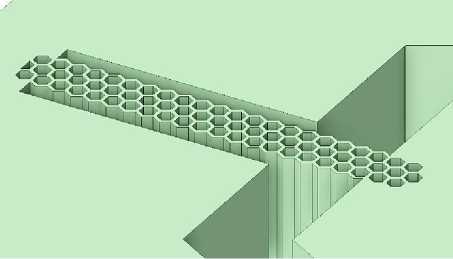
На рисунке 4 показан фрагмент модели ММА с подвесом из трубок круглой и гексагональной форм, с геометрией, близкой к реально получаемой на производстве.

а)

Рис. 4. Модель подвеса ИМ – а) круглой формы; б) гексагональной

б)

2.    Расчет механических параметров и частотных характеристик

В отличие от предыдущих расчетов, предложено разместить ось чувствительности ММА вдоль оси Z, перпендикулярно оси подвеса (рис. 2а). Таким образом, обеспечивается большая подвижность ИМ и, соответственно, повышается чувствительность.

Для определения механических напряжений и деформации выполнен расчет предлагаемой конструкции с разными типами подвеса в диапазоне ускорений до 50g для постоянных значений линейного ускорения.

Для расчетов в работе использовалась САПР для решения задач механики деформируемого твердого тела и механики конструкций. Полученные результаты по напряжениям и деформации ИМ представлены в табл. 1, 2.

Таблица 1. Максимальные деформации, мкм

Ускорение, g	1	10	20	30	40	50
Трубчатая структура	0.24	2.39	4.78	7.17	9.56	11.96
Гексагональная структура	0.19	1.92	3.85	5.77	7.7	9.62

Таблица 2. Эквивалентные напряжения, мПа

Ускорение, g	1	10	20	30	40	50
Трубчатая структура	0.38	3.82	7.64	11.46	15.28	19.1
Гексагональная структура	0.45	4.51	9.02	13.53	18.04	22.55

а)

б)

в)

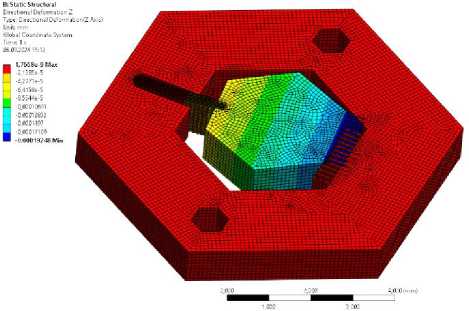
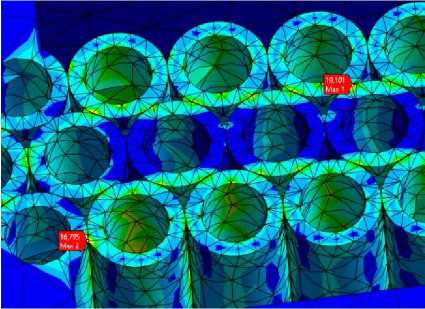
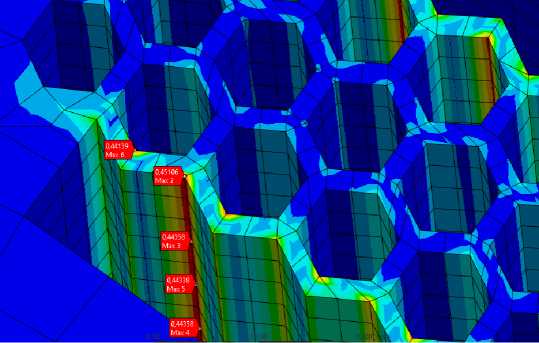
Рис. 5. Иллюстрация деформации при отклонении ИМ под воздействием линейного ускорения (а) и механических напряжений в трубчатой структуре (б) и гексагональной структуре (в)

Рассматривая поле напряжений в структуре подвеса, можно заметить важные различия в рапределении напряжений. В случае трубок видно (рис. 5б), что максимальные напряжения сосредоточены в точках спекания отдельных трубок среднего и внешних рядов, в случае шестиугольников напряжения распределены сравнительно равномерно по наружной стороне внешних рядов (рис. 5в).

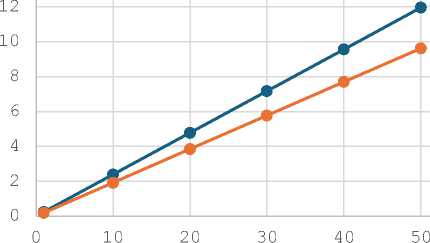
На графике (рис. 6) по результатам расчета приведена зависимость максимального отклонения ИМ в зависимости от приложенного ускорения.

Ускорение, g

Рис. 6. Смещение ИМ

трубчатая стр-ра

гексагональная стр-ра

Из графика на рис. 6 видно, что отклонение ИМ носит линейный характер. Максимальное отклонение ИМ в зоне гребенки составило 11.96 мкм для трубчатой структуры и 9.62 мкм для гексагональной структуры соответственно (см. табл.). Такие значения являются достаточным для обеспечения приемлемой чувствительности датчика.

Рассмотрим частотные характеристики ММА.

В результате проведенного модального анализа получены следующие значения пяти собственных частот (Гц): для подвеса из трубчатой структуры 1223.7, 5039.6, 8998.3, 14400, 40596; для подвеса гексагональной структуры 1363.4, 3869.7, 7244.9, 15091, 36534.

Как видно из полученных результатов расчета модели, значения собственных частот для разных подвесов близки по значениям. У модели с подвесом гексагональной структуры значение первой моды несколько выше.

Предъявляемые требования по частоте вибрационных нагрузок авиакосмической техники обычно находятся в пределах до 180 Гц [6–7], поэтому полученные значения позволяют утверждать, что возникновение резонанса в рассматриваемой конструкции ММА исключено при его применении в системах управления.

3.    Расчет изменения емкости датчика

Предлагаемая схема емкостного датчика является стандартной для такого типа МЭМС и представляет собой емкостной мост [8].

Оценить изменение емкости датчика можно по простой формуле, которая выводится из формулы емкости плоского конденсатора:

εε0S d, где ε – диэлектрическая проницаемость среды между обкладками конденсатора (для воздуха – 1), ε0 диэлектрическая постоянная, S – площадь, d – расстояние между пластинами.

Изменение емкости при смещении пластин гребенки вычисляется по формуле, которая представляет собой разность емкостей на смежных пластинах конденсаторов при перемещении гребенки на расстояние x , при условии, что x << d [9]:

ΔC=εε0S x d2

где x – смещение ИМ.

Вычисленное по данной формуле ожидаемое максимальное изменение емкости при предложенной геометрии гребенки (рис. 2в), для трубчатой структуры подвеса в рассмотренном диапазоне ускорений составляет значения от 0.14 до 7.11 пФ, а для гексагональной структуры от 0.11 до 5.72 пФ соответственно.

Таким образом, величины изменения емкости датчика достаточны для регистрации ускорений в указанных диапазонах.

4.    Обсуждение результатов

Предложена конструктивная схема ММА из перспективного радиостойкого стекла. Выполнено моделирование и расчет механических и частотных характеристик модели ММА при постоянных значениях линейного ускорения в диапазоне от 1 до 50g.

Полученные результаты численного моделирования позволяют сделать вывод о том, что предложенная схема имеет хорошие перспективы реального применения, однако требуется экспериментальное подтверждение полученных результатов.

Сравнительный анализ результатов расчета механических и частотных характеристик для модели с подвесом ИМ из трубок круглой и гексагональной форм показал, что различия незначительны. В случае деформаций и напряжений выигрывает трубчатая структура подвеса, у которой при одинаковых ускорениях большее смещение ИМ и меньшее напряжение, а в случае частотных характеристик большее значение первой моды имеет гексагональная структура, т.е. лучшая устойчивость к вибрационным нагрузкам. Однако эти различия незначительны, поэтому выбор подвеса ИМ, на взгляд авторов, необходимо принимать из других соображений.

Предполагается, что подвес ИМ из трубчатой структуры имеет слабую устойчивость к разрушению ввиду того, что спекание между отдельными трубками происходит по очень малой площади, в точке касания (рис. 3а) и максимальные напряжения сосредоточены именно в этих точках (рис. 5б). Поэтому при максимальных напряжениях высока вероятность разрушения подвеса. Совсем другая ситуация с гексагональной структурой подвеса. В этом случае подвес представляет собой сплошную структуру из сот, в которой напряжения распределены сравнительно равномерно по наружной стороне внешних рядов элементов, его составляющим.

Таким образом, можно сделать предположение, что гексагональная структура подвеса имеет более высокую устойчивость к разрушению при высоких ударных и вибрационных нагрузках.

Безусловно, следует учесть тот факт, что при расчетах использовалась идеальная геометрия структур подвеса, и в реальном изделии их форма будет несколько отличаться (неидеальная окружность, шестигранники со скругленными углами и т.д.), но качественно на общую картину полученных результатов это не повлияет.

Также следует отметить, что, используя разработанную модель, возможно подобрать необходимую чувствительность ММА для разных диапазонов ускорений путем изменения структуры и геометрии трубок подвеса ИМ.

Кроме того, необходим анализ возможных остаточных напряжений [10, 11] в подвесе ИМ ММА, которые характерны для рассматриваемого в статье материала, а также анализ поведения предложенной конструкции при воздействии переменных ускорений и вибрационных нагрузок, что является предметом дальнейших исследований.

На момент написания статьи ведется проработка и обсуждение возможности изготовления опытных образцов ММА по предложенной модели.