Исследование вопроса о существовании периодических решений

В статье приведен метод успешного построения указанной дифференциальной системы. Получен не только критерий существования периодических решений, но и методы построения этих решений, основанные на численном интегрировании указанной дифференциальной системы.

В настоящей статье изучаются свойства инвариантных множеств динамических периодических систем, определяющих уходящие движения. Предложена методика свертки фазового пространства в многомерный тор таким образом, что инвариантные множества, соответствующие предельным множествам уходящих движений, оказываются ограниченными. Получены необходимые и достаточные условия устойчивости таких множеств.

Постановка задачи. Сначала рассмот рим систему обыкновенных дифференциальных уравнений:

^X s I s ( ^X 1 ’ ■■■’ ^Xk ’ V’ ■■■’ ^ n — k ) ’

Z j = g j ( x_b ■■■’ X k , .... Z 1 ’ .... z_n _ _k ) ’ (1)

s = 1’ ■■■’ k’ j = 1’ ■■■’ n — k^

Условия существования и единственности решений системы (1) будем считать выполненными. Пусть правые части системы (1) являются периодическими функциями

Z 1 , ..., z_n _ ^ с периодом 2л. Пусть решения системы (1) являются уходящими по

^Z 1 , ..., ^zn - k , ^т. ^е."

• 1)    существует неограниченная последовательность значений параметра { t_n ] : t_n ^ да , п ^да

выполнено x_s ( t_n ) ^ x_s е ( -да, +да ) ;

• 2)    для любой неограниченной последовательности    { t_n ] : t_n ^ да выполнено

п^да zj (tn ) > да

Рассмотрим решение системы (1) с начальными данными:

х0, х0, ■■■, х0, zy = ^у + 2лmj, j = 1, .... и - к, §° е [0,2л], где mj целые. Если в системе (1) сделать замену переменных Zj = ^j + 2лщ^ то правые части не изменятся, система перейдет «сама в себя»:

X, = fs (X, Е),   ^j = 9i (X, Е), s = 1, ■■■, к, j = 1, ■■■, и - к

Исследуем вопрос о существовании периодических решений у систем дифференциальных уравнений в частных производных. Рассмотрим сначала систему уравнений

Яг- m Я г J XX

+ Е f^^l X CkXj + X D^Zj + 9к (t) ft    к=1 fzk (j=1 J j=1 J пm

= X X/^j + X BijZj + ft (t), г = 1, ..., j=1/ n.

Будем считать, что матрицы А размерности п х п, В размерности п х m, С размерности m х п, D размерности m х m, векторные функции ^f = ^{( f} 1^, ■■■^{, f}n ^{) ,} 9 = ⁽ 9 1 ■ ■■^, д_т ⁾ являются 2л-периодическими функциями независимой переменной t. Наша задача будет заключаться в установлении условий, при которых у системы (1) существует 2л-перио-дическое по t решение

X(t,Z) (3)

и в построении этого решения. Наша задача будет решена, если будет найдена кривая Х у = X y (Z), или, в параметрической форме,

Х0 = X(t), Z = Z(t), которая, являясь начальным условием задачи Коши для системы (2), определяет 2л-пе-риодическое решение (3).

Введем в рассмотрение векторы

*

^ = ( X_b ■■■, X n , Z_v ■■■, Z m ) ^,

Ф ⁽А, ■■■, ^fn , ^д1 , ■■■, ^дт ⁾ и рассмотрим линейную систему ■

^ = Р^,                (4)

где Р — блочная матрица

Р =

f ^{А В} 1 I ^{С D} J.

Пусть Y(t) — фундаментальная матри ца системы (4). Разобьем ее на блоки размеров, соответствующих размерам матриц А, В, С, D:

f ^ 11 ^ 12 1 1^ 21 ^ 22 J.

Теорема 1. Если матрица Y₁₁(2л)— Е является неособенной, то у системы (1) существует единственное 2л-периодическое решение (4).

Доказательство. Введем обозначение

Y ( t , т ) = Y ( t ) Y ¹ ( т ) . Приступим к изучению поведения решений системы дифференциальных уравнений характеристик системы (1) по отношению к координатам X 1 , ..., x_n . Решение систем дифференциальных уравнений характеристик системы (1) имеет вид:

t

^ = У^ о + f У ( t, т ) Ф ( т ) ^т.       (5)

t o

Отсюда

X = Y_nX y + Y 2 Z 0 + f ( Y_n ( t, т ) f ( т ) + ^{t 0}                             (_fi)

^{+ y} 12 ( ^{t , т} ) 9 ( ^т ) ) d ^{т ,}

Z = Y 2 _tX y + Y 22 Z 0 + f Y 2! ( ( t, т ) f ( т ) + ^t 0

^{+ y} 22 ( ^t , ^т ) 9 ( ^т ) ) dt.

Положим t = 2л, Х(2л) = X 0 . Тогда из последних соотношений получим

Х _й = ( Е - Уц ( 2л ) ) ¹ ■

2л                           4

^y 12 ( ^{2 л} ) ^Z 0 + f ( ^у 11 ( t, т ) ^f + Y 12 9 ) ^т ^t 0                            J

Подставим (7) во вторую группу формул (6) и выразим Z o как функцию t, Z : Z o = ^ ( t, Z ) . Теперь, исключив Z o из выражения (6), получим функцию

Х о = Х ( t, Z ) , (8) которая, будучи заданной в качестве начального условия задачи Коши при t = 0, определяет 2л-периодическое решение системы (2). Чтобы убедиться в этом, достаточно повторить весь ход рассуждений в обратном порядке. На этом и закончим доказательство этой теоремы.

Рассмотрим систему дифференциальных уравнений

X _ F ( t , X , р ) , (9) где вещественная и непрерывная по совокупности своих аргументов векторная функция F задана при t е ( -те, +те ) , Х е Е „ , р е [ 0, р ] . Независимая переменная t фактически входит в правую часть системы (9), которая является 2л-периодической функцией ЧХ е Е_п . Пусть, кроме того, выполнены условия теоремы существования и единственности решений системы (9) в любой конечной области G с Е_и при t е ( -те, +те ) .

Рассмотрим вопрос о существовании периодических решений у системы (9) при р = 0, т. е. рассмотрим систему

X = F ( t , X ) , (10) где функции F удовлетворяют всем условиям, наложенным на правую часть системы (9). Для решения поставленной задачи попытаемся построить в Е_п динамическую систему, определяемую системой дифференциальных уравнений, решения которой сходятся к точке X⁰, обладавшей тем свойством, что решение Х ( t , X ° , t ₀ j системы (10) будет 2л-периодическим [2].

В случае успешного построения указанной дифференциальной системы мы получим не только критерии существования периодических решений, но и методы построения этих решений, основанные на численном ин тегрировании указанной дифференциальной системы.

Введем следующую функцию переменного Z е Еи:

V ( Z ) = Z - Х ( 2л,Z,0 ) .        (11)

Функция V(Z) определена в любой точке Z е Еп, это следует из условий, наложенных на систему (10). Потребуем, чтобы функция V(Z) удовлетворяла на решениях искомой дифференциальной системы дифференциальному уравнению dV _ dt

Здесь и далее т — параметр искомой дифференциальной системы. Из этого следует:

'    DX ( 2л,Z,0 ) ) dZ

Е -               =

DZ    J dt        (13)

= -Z + Х ( 2л, 2,0 ) .

Умножим это соотношение слева на матрицу ( Е - ВХDZ) ¹ ; получим искомую дифференциальную систему:

I -

dt=(е -р ( z))-1 (-z+х ^,z,o)), где p (Z) = DX (t ^0)

^{1 )} DZ

■ t=2л

Матрица P(Z) удовлетворяет следующему дифференциальному соотношению:

. _ ^D F ( ^X, t ) DX ^

где матрица Якоби DF ( Х, t )/ ВХ вычисляется при Х = Х ( t,Z,0 ) .

Таким образом, если матрица P(Z) не имеет собственных чисел, вещественная часть которых равна единице, то правая часть полученной дифференциальной системы определена. Матрица P(Z) находится как решение задачи Коши для линейной системы (14) с начальным условием P = Е при t = 0. Значение матрицы P(Z) берется в момент t = 2л.

Для того чтобы функция V(Z) экспоненциально стремилась к нулю в силу построенной дифференциальной системы при т ^ те , достаточно, чтобы решение Z = Z ( т,Z 0 ) , где

Z q е E_n построенной дифференциальной системы было неограниченно продолжаемо в положительном направлении [1].

Если требование (12) можно заменить на следующее:

dV d t

kV,

где к — некоторая положительно определенная матрица, и матрицу к выбрать в виде к = ( Е - Р ( Z ) )( Е - Р ( Z ) ) * , то система дифференциальных уравнений примет вид

ния последовательности { Z k } . Для простоты возьмем за основу метод Эйлера интегрирования систем дифференциальных уравнений.

1. Выбирая некоторое положительное целое число N, оценку величины которого можно получить из (12) и погрешности метода Эйлера, строим последовательность X q = Z q ,

^X k + 1

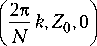
k = 1, ..., N.

Ц = ( Е - Р ( Z ) ) * ( -Z + X ( 2 л , Z , 0 ) ) .

2. Вычисляем значение P ( Z q ) следую-

щим образом: P q = Е,

Лы = Л

В случае продолжаемости решения Z = Z ( t , Z q ) этой системы в положительном направлении будем двигаться по этому решению, например, с помощью численного метода типа Рунге — Кутты. Поскольку решение Z = Z ( t , Z q ) сходится к значению X⁰, определяющему периодическое решение системы (10), причем траектория попадает в s-окрестность точки X⁰ за конечное время (оценку можно получить из (12), то можно доказать, что путем выбора параметров численного метода можно построить последовательность { Z k } , сходящуюся к X⁰ [4].

Все вышеизложенное можно резюмировать в следующей теореме.

Теорема 2. Если существует точка Z q е Е_п такая, что решение Z = Z ( t , Z q ) системы (15) неограниченно продолжимо в положительном направлении, то это решение при т ^ да , сходится к значению X⁰, определяющему периодическое решение X ^ t , X⁰ , o j системы (10).

Перейдем теперь к алгоритму построе

_х ^DF ^ ^Хк ) _р

DX ^к ’

2л

+ х

N

К = — к , к = 0, ..., N - 1, ^к N

Р ( Z q ) = P_N.

3. Вычисляем Z ^ по формуле

Z _v = Z q + ^ ( Е - Р ( Z _o ) ) * ( - Z _o + X ( 2 л , Z q , 0 ) ) .

Таким образом, строится последовательность { Z k } . Критериемокончаниябудетбли-зость к нулю функции У, критерием выбора шага интегрирования будет неравенство

||V( ^Zk ₊ i)|| <  ||^V ( ^Zk)|| .

Выводы. В данной статье вопрос о существовании периодического решения системы (10) сведен к вопросу о существовании продолжаемого решения системы (13). На основании многих известных достаточных признаков продолжаемости [3] можно предложить несколько достаточных условий существования периодического решения системы (10).