Исследование возможностей медианной фильтрации при цифровой обработке изображений совокупностей локальных биологических объектов

Цифровая обработка регистрируемых изображений локальных биологических объектов является основой принципа действия ряда современных аналитических приборов, например анализатора субпопуляций клеток [1, 2]. Под локальными объектами здесь понимаются объекты, в данном случае микроскопические изображения клеток, геометрические размеры которых существенно меньше размеров полного кадра изображения. Задача начального этапа анализа заключается в различении и идентификации предварительно обнаруженных объектов [1] на основе совокупности нескольких параметров их изображений [2]. Из геометрических параметров, используемых для идентификации биологических клеток, например клеток крови, определяющим является размер, поэтому в качестве бинарной геометрической модели клетки обычно принимается круг, диаметр которого или радиус необходимо установить в процессе обработки изображения.

Регистрируемые изображения проб объектов при медико-биологических исследованиях сопровождаются биологическими шумами и дефектами. Так, например, на рис. 1, а, показана проба крови с большим количеством "мусора" — остатками разрушенных клеток в процессе пробоподготовки, которые идентифицируются как объекты с размерами, меньшими чем размеры любых клеток крови. Эти объекты можно отбраковать по размерам после их обнаружения и измерения параметров [1, 2]. Однако целесообразнее устранить такие объекты в самом начале процесса обработки, чтобы не тратить время на их обнаружение, измерение па- раметров и идентификацию.

На рис. 1, б, показана проба крови, содержащая гранулоциты — клетки, имеющие внутреннюю структуру, выражающуюся в наличии гранул, которые в видеоизображении резко выделяются на фоне клетки. В работе [2] показаны проблемы, возникающие при измерении размеров подобных клеток, — процедура измерения размера клетки может дать результат, соответствующий размеру гранулы. В упомянутой работе для устранения этого эффекта использовано устранение гранул на основе анализа локальной гистограммы видеосигнала. Однако следует отметить, что малые размеры исследуемых объектов, характеризующиеся малым количеством пикселей, содержащихся в их изображении, часто не позволяют построить качественную и надежную локальную гистограмму.

Широко известен способ устранения мелких деталей изображения и случайных выбросов при помощи медианной фильтрации видеосигнала [1, 2]. В процессе медианной фильтрации значения сигнала в некоторой окрестности точки, в которой вычисляется отклик фильтра, при помощи сортировки по возрастанию или убыванию выстраиваются в вариационный ряд. Отклик фильтра определяется как медиана — значение сигнала середины (центра) вариационного ряда. Следует отметить, что в случае одномерного процесса медианный фильтр совсем не изменяет монотонного сигнала, т. к. отсчеты такого сигнала уже ранжированы в окрестности рассматриваемой точки и, если окрестность (окно фильтра) симметрична относительно этой точки, данная точка и будет медианой вариационного ряда. Нет никаких разумных оснований для использования несимметричного окна фильтра.

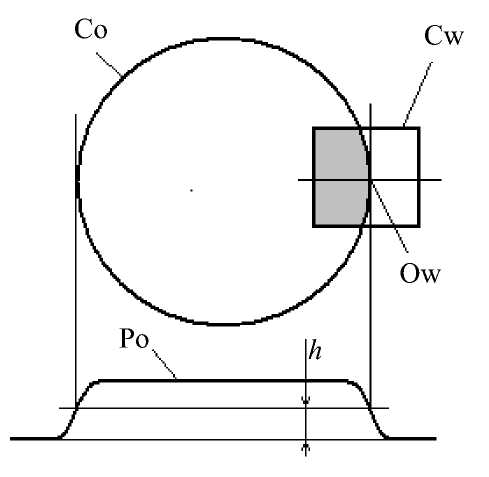
Рис. 2. Двухмерная медианная фильтрация (пояснения в тексте)

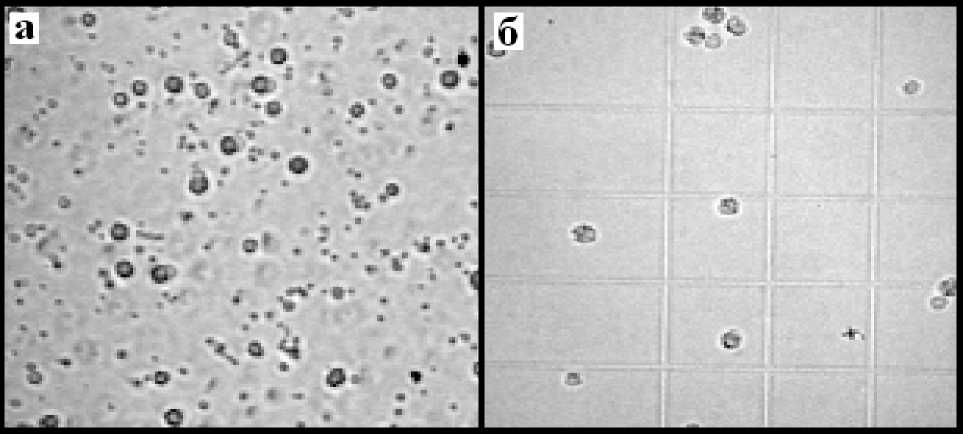
Рис. 1. Изображения объектов: а — проба клеток крови; б — гранулоциты

Поэтому медианный фильтр эффективно устраняет мелкие детали и выбросы и практически не меняет остальной части сигнала одномерного процесса, что выгодно отличает его от линейного фильтра. Основной принцип медианной фильтрации гласит: для устранения из сигнала выбросов длительностью n отсчетов окно фильтра должно содержать не менее 2n + 1 отсчетов. Только в этом случае отсчеты, соответствующие выбросу, окажутся в вариационном ряду полностью правее или полностью левее медианы. Дополнительным важным преимуществом медианной фильтрации по сравнению с методом анализа локальных гистограмм [2], является то, что медианный фильтр одинаково успешно устраняет как положительные, так и отрицательные выбросы.

Вместе с тем необходимо отметить, что для данных двухмерной информации, каковой является изображение, нет очевидного и однозначного понятия монотонности. Поэтому установленное для одномерного медианного фильтра свойство — то, что участки сигнала, не содержащие выбросов, практически не изменяются, — для двухмерного медианного фильтра в общем случае оказывается неверным. Так, на рис. 2 показан контур объекта Co, определяемый на полувысоте h его профиля Po, и контур Cw окна медианного фильтра с центром Ow на контуре объекта. Из рисунка видно, что большая часть точек в окне фильтра и соответственно в вариационном ряду будет иметь значение, меньшее h , а следовательно, и медиана будет меньше h . Следовательно, после медианной фильтрации точка Ow окажется за пределами контура объекта, который в нашем примере определяется как геометрическое место точек с величиной сигнала h . Очевидно, что это такие точки, при помещении в которые центра окна фильтра площадь окна делится контуром Co на две равные части. Для случая на рис. 2 такая точка будет левее точки Ow, т. е. ближе к центру объекта. Нетрудно убедиться, что медианная фильтрация сжимает размеры объекта.

Однако другие достоинства медианной фильтрации заставляют более подробно исследовать свойства и предельные возможности двухмерного медианного фильтра, что и является предметом настоящей работы.

ПОСТАНОВКА ЗАДАЧИ

Уточним геометрическую модель интересующего нас исследуемого объекта и выберем методы исследования. Как видно из реального примера изображения на рис. 1, а, края объекта вдоль его контура чаще всего выражены значительно более явно, чем центральная часть, что связано с особенностью прохождения оптических лучей вдоль границ раздела сред. Поэтому более адекватной геометрической моделью объекта будет не круг, а кольцо, характеризующееся внешним и внутренним радиусами.

Далее, поскольку при медианной фильтрации не важны абсолютные значения отсчетов сигнала, а имеет значение только порядок следовании отсчетов в вариационном ряду, то вполне допустимо и достаточно использование бинарной модели.

Вариационный ряд фильтра формируется по всем отсчетам сигнала внутри его окна, в данном случае двухмерного. Поэтому длина ряда равна площади окна.

Конечно же, медианный фильтр является инструментом манипулирования дискретными данными. Дискретность данных исследуемых объектов является особенно явной из-за их малых размеров — единицы и десятки пикселей. Однако для выяснения предельных возможностей метода, с точки зрения автора, допустимо и удобнее пользоваться непрерывными моделями и методами, что позволит использовать хорошо разработанный аппарат математического анализа и геометрии. В соответствии с этим выбором мы пока оставим в стороне категорию вариационного ряда и будем оперировать непрерывными площадями соответствующих объектов.

Это приводит нас к следующей формулировке основного требования к медианному фильтру: для устранения выбросов сигнала площадью Sn площадь окна фильтра Sw должна быть более чем в 2 раза больше Sn . С другой стороны, фильтр не должен удалять объект или какой-либо его фрагмент, пусть и с неизбежными, как показано выше, искажениями. Как нетрудно понять из рис. 3, в наилучшей степени этим противоречивым требованиям удовлетворяет фильтр с круглым окном. На этом рисунке Co — внешний контур кольцеобразного объекта, Cw — контур окна фильтра (на рисунке он как раз некруглый), Ns — удаляемый выброс.

Основной задачей настоящей работы является определение степени искажения размера объекта медианным фильтром и установление возможно-

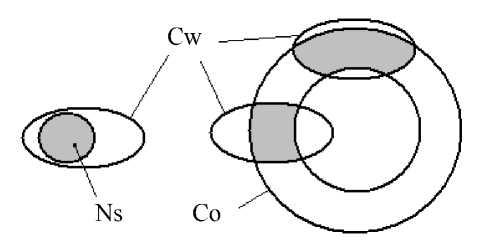
Рис. 3. Влияние формы окна медианного фильтра на результат медианной фильтрации (пояснения в тексте)

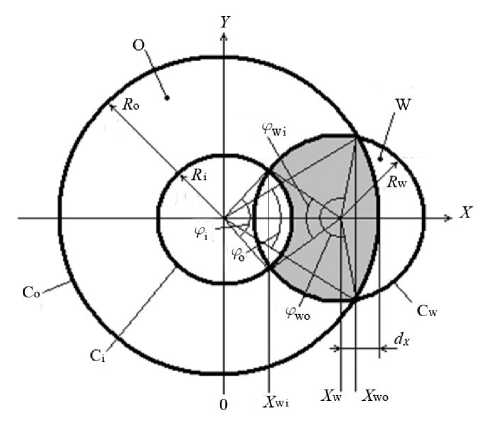
Рис. 4. Геометрическая модель процесса медианной фильтрации (пояснения в тексте)

сти учета этого искажения или корректировки размера при последующей обработке информации.

МЕДИАННАЯ ФИЛЬТРАЦИЯ

На рис. 4 представлены: объект О с внешним Co и внутренним Ci круглыми контурами радиусами соответственно R o и R i, а также круглое окно медианного фильтра W с контуром Cw и радиусом R w. X w — положение центра окна относительно центра объекта. Остальные обозначения ясны из рисунка.

Для определения положения контура объекта после медианной фильтрации сначала необходимо вычислить площадь той части исходного объекта, которая попадает в окно медианного фильтра. Для начала на основании формулы уравнения окруж- ности можно получить координаты Х для положения точек пересечения контуров

R o² - R w² + X w² X wo =

2 X w

R i² - R w² + X w²

S wo = 2 R W2 ^ wo - sin Ф wo ),	(8)
S i = 2 R i2( ф 1 - sin Ф , ),	(9)
S wi = 2 R w2( Ф w1 - sin Ф w1 ).	(10)

Соответствующие углы на рис. 4 определяются

X w - X wo Ф wo = 2arccos           , R w	(3)
X w - X wi Ф w1 = 2arccos           , R w	(4)
X w Ф = 2arccos---, o            R o	(5)
X wi Ф = 2arccos----. i               R i	(6)

Площадь объекта, попадающая в окно фильтра, складывается из суммы площадей (см. рис. 4) правого сегмента круга, ограниченного контуром Со, и левого сегмента круга W, опирающихся на (вертикальную) хорду через X wo — S o, S wo, за вычетом площадей сегмента круга, ограниченного контуром Ci, и сегмента круга W, опирающихся на (вертикальную) хорду через X wi — S i, S wi.

На основании формулы для площади сегмента круга имеем:

^S о = 2 ^R o^{2 ф}

— sin Ф о ) ,

Искомая площадь в конце концов является функцией четырех исходных параметров

S ( R o , R i, R w, X w) = ( S o + S wo) – ( S i + S wi) .   (11)

Измеренное значение радиуса объекта R mo после медианной фильтрации будет равно такому значению X w, при котором площадь S будет равна половине площади окна фильтра. На основании этого получаем следующее основное уравнение, описывающее процесс медианной фильтрации в рассматриваемом случае:

F ( R o, R i, R w, R mo) =

= S ( R o, R i, R w, R mo) - 1 n • R w² = 0.      (12)

Как достаточно ясно видно из рис. 4, что и подтверждается численными расчетами, уравнение (12) в общем случае может иметь два корня — больший корень дает новое значение внешнего радиуса объекта, меньший корень — внутреннего радиуса ( R mi), т. е.

F ( R o, R i, R w, R mi) = 0.             (13)

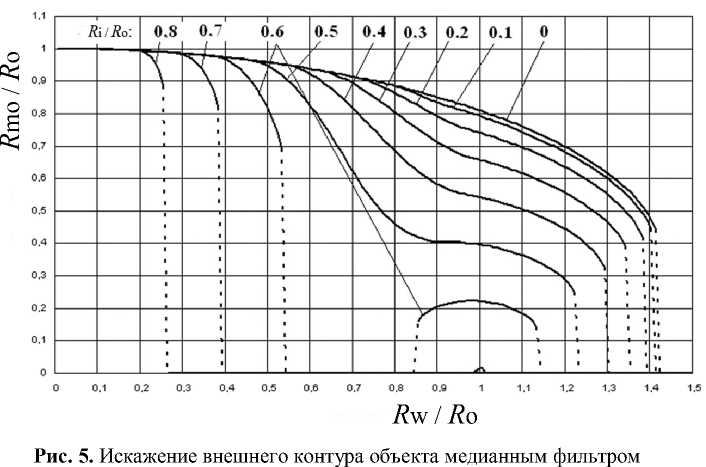
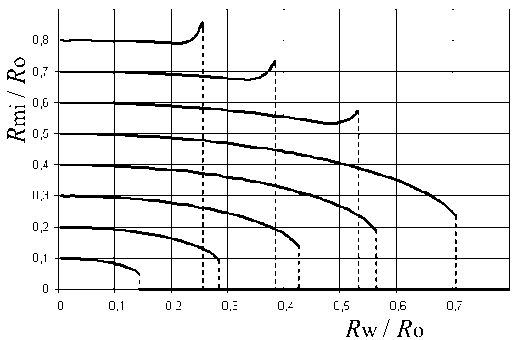
Рис. 6. Искажение внутреннего контура объекта медианным фильтром

d R o / R w

R mo / R w

Рис. 7. Поправка, компенсирующая искажение объекта медианным фильтром

Уравнения (12) и (13) аналитически в явном виде не решаются. Поэтому было выполнено численное решение этих уравнений относительно R mo и R mi . Результаты расчетов приведены на рис. 5 и 6 в нормированном виде. Эти рисунки иллюстрируют степень искажения объекта медианным фильтром, нас же окончательно интересует реальный исходный размер объекта R o, а не измеренный после фильтрации R mo .

В принципе R o можно было бы восстановить по измеренной величине R mo на основании данных, представленных на рис. 5, если знать величину R i . Однако, восстановить R i по величине R mi не всегда возможно. Внутренний "пробел" в изображении объекта может быть удален медианным фильтром как отрицательный выброс, о чем свидетельствуют разрывы графиков в нижней части рис. 6. Однако величина R i может быть непосредственно измерена на исходном, нефильтрованном изображении. При этом если гранула оказывается во внутренней части клетки, она обычно сама "съедает" внутренний "пробел" (если он есть), не меняя остальной части изображения, и проблема исчезает.

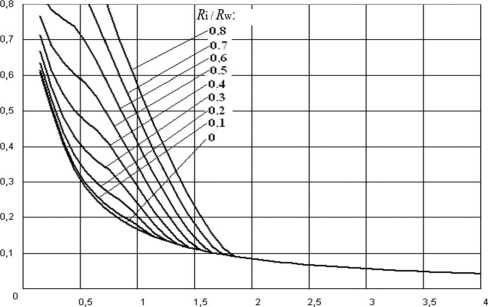
На рис. 7 приведены нормированные графики поправки d R o для расчета R o, т. е.

R o = R mo + d R o( R mo , R i), (14) рассчитанные на основании уравнения (12).

РЕЗУЛЬТАТЫ И ВЫВОДЫ

Проверка полученных соотношений на моделях больших размеров, когда дискретность данных сказывалась мало, показала хорошие результаты.

Рис. 8 . Измерение размера гранулоцита.

а — измерение размера без использования медианной фильтрации; б — измерение размера после медианной фильтрации изображения объекта; в — измерение размера с использованием медианной фильтрации и корректировки искажений, вносимых фильтром

Проверка на реальных объектах производилась на изображениях, полученных при помощи прибора ДСКФ1. На этих изображениях размер объекта (его диаметр) составлял единицы пикселей. В этом случае о круглом окне медианного фильтра можно говорить весьма условно. Поэтому в качестве параметра радиуса окна R w использовался эквивалентный радиус — это радиус круга, площадь которого равна площади окна фильтра.

На рис. 8 приведены результаты измерения размера клетки, изображенной в центре рис. 1, б, при различных вариантах обработки информации. На рис. 8, а, показан результат измерения размера без применения медианной фильтрации. В этом случае, как видно из рисунка, алгоритм измерения размера "зацепился" за гранулу и дал существенно заниженный результат. После медианной фильтрации (см. рис. 8, б) фильтром с окном 3×3 пикселя гранула была удалена и результат оказался близким к реальному. Далее после корректировки размера объекта в соответствии с изложенным в настоящей работе подходом окончательный результат (см. рис. 8, в) следует признать вполне удовлетворительным.

Таким образом, медианная фильтрация является удобным и надежным инструментом при цифровой обработке изображений в процессе измерения параметров локальных объектов.