Исследование возможностей решения в замкнутом виде задачи Коши для линейных интегро-дифференциальных уравнений Фредгольма с запаздывающим аргументом

Статья посвящена исследованию возможностей решения в замкнутом виде задачи Коши для линейных интегро-дифференциальных уравнений Фредгольма с запаздывающим аргументом.

Investigation of solving in the close type capabilities for a Cauchy problem for linear integral differential Fredholm equations with time delay

The article is devoted to the investigation of solving in the close type capabilities for a Cauchy problem for linear integral differential Fredholm equations with time delay.

В работах [3]-[4] исследованы возможности преобразования начальных задач для линейных интегро-дифференциальных уравнений Фредгольма с запаздывающим аргументом к разрешающим интегральным уравнениям с обыкновенным аргументом. Используя одну из модификаций функций гибкой структуры показано, что задача Коши для всех уравнений запаздывающего типа преобразуется к разрешающим интегральным уравнениям смешанного типа Вольтерра-Фредгольма с обыкновенным аргументом. Для уравнений нейтрального и опережающего типов выявлены виды уравнений, для которых такое преобразование возможно.

Сравнивая все разрешающие уравнения, полученные в этих работах , видим, что начальные задачи для рассматриваемых типов и видов интегро-дифференциальных уравнений Фредгольма с запаздывающим аргументом сводятся к разрешающим интегральным уравнениям смешанного типа Вольтерра-Фредгольма фактически одного и того же вида

, viW

p(z)+£[ J Q^z^pW+

+X J ^(z,/)//(r>*]=B(z),        (1)

где для ядер Q_s#(z,0 и функции B(z), в упомянутых работах, получены определенные формулы. В работе [5] результаты исследований сведены в таблицу-схему, опираясь на которую рассмотрим возможные варианты решения таких уравнений в замкнутом виде.

Ядра Q^z^YNДг,^ и функция B(z) в своей структуре содержат неопределенные параметры r,.,i = 1,«, за счет оптимального выбора которых можно пытаться получить решения в замкнутом виде.

Во-первых, решение в замкнутом виде получим, если в уравнении (1) параметры r?, i=l,п таковы, что B(z) =0. Тогда разрешающее уравнение (1) будет однородным, его решение будет p(z) = 0 и решение первоначально поставленных начальных задач найдется по формуле функции гибкой структуры, откуда следует y^D^y^x^Az-x^ (2)

где определители D и ДДг-Хд) вычисляются по формулам для функции гибкой структуры в работе [3 J.

Другой возможный вариант решения в замкнутом виде получим, если параметры i=l,w таковы что О, (z,/)s0

Г.А. Шишкин, Исследование возможностей решения в замкнутом виде задачи Коши для линейных ин- тегро-дифференциальных уравнений Фредгольма с запаздывающим аргументом иМ,(М =0 V j = 0J. Тогда решение уравнения (1) будет p(z) = B(z) и соответственно по формуле для функции гибкой структуры определятся решения начальных задач

y(z) = ZT^y1"1^ )Д, (z - х0) +

• + py(z-0/WH-

• Если за счет выбора параметров выполнить условия B(z) = 0 или Q, (z,0 = 0 иу(тд)^0 у/ = 0Д не удается, то можно попытаться при ^(z,/)^0 сделать

В этом случае разрешающее уравнение будет интегральным уравнением Фредгольма и к нему применимы все известные методы решения в замкнутом виде интегральных уравнений Фредгольма (например, метод для вырожденных ядер).

Если же за счет выбора параметров удается сделать N^zd^O Vj = QJ при 2Дг,0*^ тогда получим разрешающее интегральное уравнение типа Вольтерра, для которых также в некоторых случаях известны возможные варианты решения в замкнутом виде.

Следует также заметить, что для некоторых частных видов разрешающих уравнений какие-то из вышеперечисленных условий могут выполняться автоматически.

Рассмотрим задачу Коши при начальном значении Хо = 0 для уравнения запаздывающего типа

У(х) + ху'(х -1) - 2 ^Tiy^dy = хе¹"¹,

• - у(х) = х,У(х) = 1 на Е^ = [0], у(х — 1) = х — 1,У(х -1) = 1 на Е^ =[-1,0]

Выпишем формулы функции гибкой структуры для п=2:

1 Г 2

у№ =--- £У1Ч)(х0)Дух-х0) +

+ Ja₃(x -t)p(l)dt

*0

У(х) =

—— [r^ -r^’"* i(r₂e^ril^^{l>      n})p(l)dt

^'Л          0

уЧх) =

-^2е'’с^'’)//(/)Л]+ц(х).

о

Для сокращения объема выкладок возьмем один из параметров равным нулю п=0 и по формулам таблицы-схемы, приведенной в работе [5], найдем

Фо(хд)= У^*^'¹, Ф^ХД) = Г,^¹^ ,

H0(x.t) = - — f^pte1

Г2 /

F(x) = xe^'-^e^- xr^1 ’*+2 jV^t/’’7 -\yh] = 0

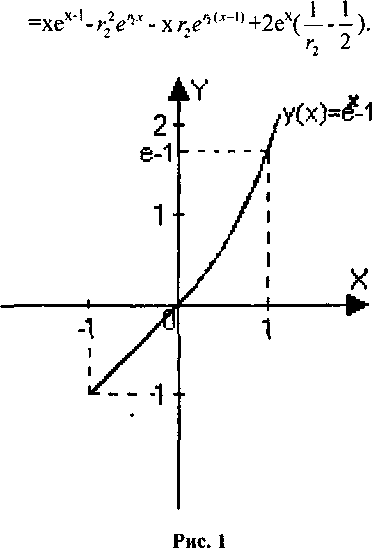
Нетрудно увидеть, что оптимальное значение параметра гд—1, при котором F(x)s0. Тогда разрешающее уравнение однородное, его решение ц(х)=0. И решение поставленной задачи будет yU) = ^ -1.

Найденная функция удовлетворяет всем условиям поставленной задачи, что хорошо видно из рис. 1.