Исследование возможности моделирования процесса резания в камере для измельчения фруктов и овощей

Профили лезвий, представленные в настоящее время на рынке, отличаются большим разнообразием и значительно отличаются от упрощенных контуров, используемых в известных расчетных моделях [1-3].

В связи с этим для практических расчетов представляет интерес рассмотрение обобщен -ного профиля лезвия ножа и получение аналитических зависимостей для определения силовых параметров его взаимодействия с материалом для большинства используемых профилей, описывая их как частные случаи. Такой профиль показан на рисунке 1, на котором представлена принятая нами расчетная схема.

Общая сила Р, действующая на резак, представляется в виде двух ее составляющих Ру и Рх, соответственно по осям у и х (рисунок 1).

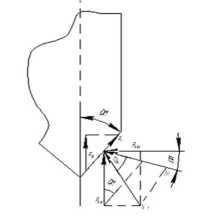
Рисунок 2. Силы, действующие на плоскость (фаску) притупления ножа

N । = f • ^{( р}сж ^sin a ^{+ р}обж cos a );      ⁽⁴⁾

F_x = n i • f ;                   ⁽⁵⁾

где f – коэффициент трения.

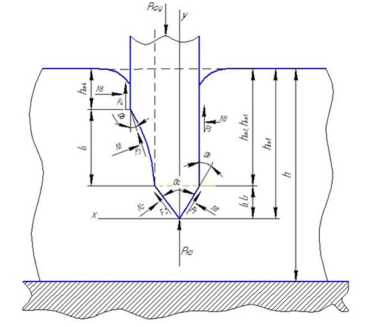
Рисунок 1. Силовое взаимодействие лезвия ножа с материалом

f = ^tg ф ;

N 1 = N 1 cos ф = Р сж + P² оюж cos a i = = ^{f ( Р} сж ^{sin a} i • ^{cos a} i ^{+ Р} о6ж ^cos 2 ^a i ) = = ^{f ( Р} сж ^{1 sin 2 a} i ^{+ Р} обж ^{cos a} i );

Элементарная сила сжатия dP сж , действующая со стороны столбика площадью dF длиной, равной единице, и стороной dx будет равна [4-7]:

dP = E • e • dh • tea,;сж        сж сж g 1 ;

Сумма сил в проекции на ось 7 (плоскость лезвия ножа):

Р кр = Р у = Р к + N i sin « 1 + F 1 COS « 1 + + N 2 sin( a 2 - a _i) + F 2 cos ( a 2 - a _i ) + + N 3 sin a 3 + F₃ cos a 3 + F₄ + F 5 ;

h рсж = ^Жх;           (8)

h где hсж.х - сжатие на расстоянии х от вершины лезвия.

Отсюда:

dP сж = E •     • dh„ ■ tg a i ;

h

Сумма сил в проекции на ось Х (плоскость материала):

P

сж

E • tg ^a i h

h сж .1

h

сж . x

^-сж .i ^- l i

• dh™

сж

E

= v- tg ^a i h

h

2 сж . x

P x = N , cos a _i - F_i sin a _i -

- N 2 cos( a ₂ - a _i) + F ₂ sin ( a ₂ - a _i ) -

- N 3 cos a ₃ + F ₃ sin a ₃ - N 4 + N 5 ;

Общая сила, действующая на лезвие:

P = p y + P X

Пусть _a 2 - _a 1 = p . Рассмотрим силы, действующие на плоскость (фаску) притупления лезвия, примыкающую к высоким спускам лезвия ножа (рисунок 2).

Etg ^ •( ^ У сж р - ^{( -}сж л ^- l i^{) 2} ).       (9)

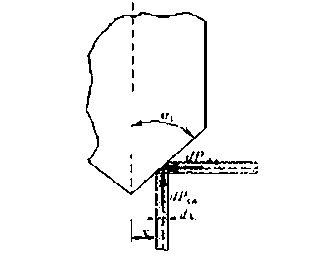
Рисунок 3. Элементарные силы сопротивления сжатию материала лезвием

Принимаем ( h_{сж .1} - l ₁ )= h    , тогда:

^.                 сж .

E ⋅ tg α _{1 2       2}        E ⋅ tg α ₁

сж.1      сж.2

сж    2h2

гдеα = (h2сж.1 - h2сж.2);

ющих соображений [8-10]. Примем, что деформация сжатия и обжатия материала по боковым плоскостям меняется по закону треугольника (рисунок 4).

P

обж

E ⋅ µ    h сж .1

∫ ^h h h сж .1 - l 1

⋅ dh

сж

E ⋅ µ h сж .1 ∫ ^h h h сж .1 - l 1

⋅ dh

сж

E = µ h

² сж . x

E

= µ α ; 2 h

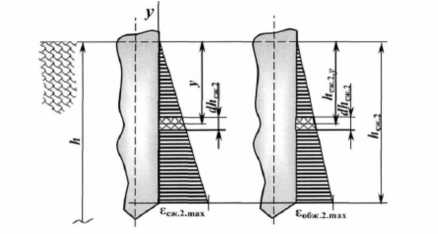
Рисунок 4. Эпюры относительных деформаций сжатия и обжатия

Усилие на режущей кромке Р к равно:

Pk = δ ⋅ σp ;           (11)

где δ - ширина кромки (длина принята за 1); σp - разрушающее контактное напряжение под кромкой лезвия.

Члены уравнения (11):

h сж.2 у

εсж 2 =        ;

h обж2    обж2        сж2 ;

Для участка единичной длины:

dP- т - 8 - ^-E-dh ₉ 7; (18) обж 2     обж 2        сж 2

' E

F ₁ = F ₁cos α ₁ = f (_{4 h} α ⋅ tg α ₁ ⋅ sin2 α ₁ + ₍₁₂₎

E

+ µ ⋅ α ⋅ cos² α );

2 h           ¹

E 2

N ⋅ sin α = A = tg α ⋅ α ⋅ sin ² α + 1            1 y 2 h 1                    1

где ε _{обж 2} ⋅ Е - напряжение обжатия.

h dP = µ ⋅ сж2y dh   ⋅ E;

ож             сж

h

+ µ α ⋅ sin 2 α ;

4 h             ¹

Принимаем α ₂ - α ₁ = β и b = ( h ² сж .1 - h ² сж .3 ) , тогда:

где µ ^{hсж 2 у} h

h сж2 у

= ε сж .2 у

ε обж .2 у

h сж 2 у             у

εсж.2max      = εсж.2max hh сж2             сж2

E 2

N sin β = C = tg β ⋅ b ⋅ sin ² β +

2              y 2 h

обж .2max     сж .2max µ ;

ε обж .2 y = ε сж .2 max ⋅ µ ⋅ h сж .2 у

E

+ µ b sin 2 β ;

4 h

F ₂ cos β = D_y = F ^' 2 =

f ( ^E tg β sin2 β ⋅ b + µ ^E b cos² β );

4h2

E ₂

N sin α = G = tg α ⋅ c ⋅ sin ² α +

3       3 y 2h 3             3

E

+ µ c sin 2 α );

4h где c = (hс2ж.3 -hс2ж.А);

F ₃ cos α ₃ = H_y = F ^' 3 = f ( ^E tg α ₃ sin 2 α ₃ ⋅ c + (16) 4 h

E 2

+ µ c cos α ₃ );

Силы N4 и N5, действующие на боковые плоскости лезвия ножа, определим из следу- hсж.2у      y

µ ;

h h .

сж .2

где у= h     , тогда:

сж . у

ε обж .2 y

h сж.2 у где         εсж.2у .

h h з сж .2 у µ;

h

Величина dP обж . 2 является произведением ( ε     ⋅ Е ) на площадь ( dh   ⋅ 1), т.е.:

о ж.2 y                              сж hсж2y dPобж2 = µ⋅       dhсж2 ⋅ E ⋅1;

h тогда:               Ehсж2               E h2сж2

N ₅ = P_{обж 2} = µ ⋅      h _{сж 2 у} ⋅ dh _{сж 2} = µ ⋅        ;

h                  2 h

Сила трения F5 соответственно равна:

F 5 = P обж 2 ⋅ f = µ ⋅ ^{Eh 2 сж 2} ⋅ f ;     (19)

2 h

E h ² сж 4

Аналогично: N = µ ⋅         ; (20)

4       2 h

dP сж

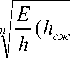
- ^x ) dx ; tg α ₁

E h сж 4

F ₄ = f ⋅ µ ⋅           ;

2 h

тогда сила Р сж равна:

h c ; ⋅ tg α 1

P сж = ∫ ( ^E ( h 0 h

сж

-

1 x

) ⁿ dx ; tg α ₁

Рассмотрим силы в проекции на ось

«X»

Интеграл вычисляется методом подста-

новки. Обозначим:

(в плоскости разрезаемого материала и опорной полочки).

EE

N ⋅ sin α = A = tg α ⋅ α ⋅ sin α cos α + µ α ⋅ (cos α )

• 1          1 x 2h 1               1         1        2h

EE

• =    tg α ⋅ α ⋅ sin 2 α + µ α ⋅ cos α ;

4h 1               1       2h

• F sin α = B = α ⋅ tg α ⋅ sin ² α + µ ⋅    α ⋅ sin 2 α ;

• 1        1 x    2h           1            1         4h

EE

N cos β = C = tg β ⋅ b ⋅ sin 2 β + µ b cos ² β ;

• 2            x   4h2

( h сж

-

тогда:

F ₂ sin β = D_x

N ₃ cos α ₃ = G_x

F ₃ sin α ₃ = H_x

EE

=    tg β sin² β ⋅ b + µ b cos 2 β ;

2h4

EE

= tg α ⋅ c ⋅ sin 2 α + µ c cos ² α ;

4h     3             3      2h

E2

= tg α sin ² α ⋅ c + µ c sin 2 α ;

2h     3        3         4h

N ₄ = µ ⋅

E h сж 4

2 h

;

N ₅ = µ ⋅

E h сж 2

2 h ^;

Возможны частные случаи для лезвий ножей с различной геометрией, вытекающие из обобщенной зависимости напряжений от деформации [11-13]. Если степень п в такой зависимости не может быть принята равной 1, исходная для расчетов сила сжатия Рсж определяется следующим образом.

Согласно общей формулы имеем:

σ = ⁿ ε сж ⋅ E ;           (22)

согласно рисунку 2:

dPсж = ⁿ ε сж ⋅ E ⋅ dF , dF = dx ⋅ 1; (23)

где dPсж — сила обжатия со стороны столбика площадью dF. При этом ширина столбика равна dx, а длина принята равной 1. Относительное сжатие ɛ сж и сила dP сж соответственно равны:

x

) = m , tg α ₁

dm = -

dx ;

tg α ₁

dx = - tg α ₁ ⋅ dm ;

После подстановки имеем:

P сж

E 1 h_{c ;} ⋅ tg α ₁

= ( )n ⋅     ⋅ mn ⋅ (-tgα )dm = h1

_E 1 h c ; ⋅ tg α 1     ₁

= ( ) ⁿ ∫ ₁

h 0      + 1

n

1 + ₁

⋅ m ⁿ ( - tg α ₁);

Показатель степени в формуле определяется физико-механическими свойствами материала и скоростью протекания процесса резания [14-16]. В том случае, когда ее величина оказывает существенное влияние на сопротивление материала деформации необходимо учесть следующее.

При деформировании сжатием материалов (в том числе лезвием режущего инструмента) с небольшой скоростью, скорость распространения деформации обычно близка к скорости деформирующего воздействия (движения режущего инструмента). Поэтому в материале деформации распространяются относительно равномерно (в зависимости от геометрических параметров лезвия). Однако при высокоскоростном деформировании, когда скорость воздействия существенно превышает скорость деформирования, распределение деформаций внутри материала не является столь однородным: деформации концентрируются вблизи режущей кромки.

Известно, что скорость волны деформации для материала в упругом состоянии равна скорости звука. В том случае, когда материал утратил упругие свойства, при распространении волны пластичности в результате деформирующего воздействия на него кромки лез-

вия имеет место следующее соотношение скорости воздействия (резания) v i и, деформации у края волны деформации ε i , (на некотором элементарном участке):

^{ε 1             ε i} 1 ¹ ∂ σ ¹

v_i = v_д ⋅ d ε = ( )² ⋅ (    )² d ε ;    (29)

0        0 ρ ∂ε где vд - скорость распространения деформации; σ — напряжение.

Вид графической зависимости «напряжение-деформация» для материалов предполагает, что вблизи предела ∂σ текучесть — ∂ε стремится к нулю. Поэтому скорость деформирующего воздействия на материал достигает максимума при некотором критическом значении деформации εi. При внедрении лезвия в материал с более высокой скоростью vi=viкр волна деформации не может распространяться от деформируемого участка, что и способствует разрушению материала.

Таким образом, eсли сила, вызвавшая движение элементарных частиц материала с упругопластическими свойствами (нaпример, кожуры) действует очень кратковременно, то область, в которой за время действия силы возникли деформации и скорости, будет очень узкой. При этом распространение деформации по слоям материала не сопровождается расши- рением той области, в которой вначале были локализованы деформации и скорости. Вследствие того, что эта область очень узка, деформации и скорости в каждом слое материала будут появляться на очень короткий промежуток времени - по материалу с конечной скоростью будет распространяться короткий импульс деформаций сжатия и скоростей. Значения величины деформации и скорости ее распространения связаны между собой через параметры, характеризующие упругость и пластичность среды объекта обработки. Следовательно, скорость зависит от свойств тела, в котором импульс распространяется. В большинстве материалов скорость распространения импульса оказывается порядка 5 103 м/с.