Исследование задержки в системе G/G/1

Как известно из теории СМО [1], среднее время ожидания требований в очереди является составной частью задержки в сетях пакетной передачи данных. В классической СМО M/M/1 оно выражается равенством (здесь и далее используется классическое трехпозиционное обозначение Кендалла):

для системы M/G/1:

W =

с коэффициентами вариаций интервалов поступления и обслуживания квадратичной зависимостью, так как дисперсия случайной величины и коэффициент вариации связаны соотношением             . Таким образом, среднее время ожидания в очереди в системе с входными распределениями, имеющими коэффициенты вариаций интервалов между требованиями входного потока и времени обслуживания меньше, чем в системе M/M/1, и меньше, чем в системе M/G/1 при , и меньше, чем в системе G/G/1 при условии              , при оди наковой нагрузке:

^ |(с,<4

<1)< W | (с, = 1,^, =1)< ^

Наконец, для системы G/G/1 это время равно

(^СЛ = t с„

>1)<^ | (с, > 1, с/( > 1) .

W

D.+D^+a-pf/r f-

1(\-р)/Х

Неравенства (4) также отражают непреложные факты из теории СМО.

В этих формулах использованы следующие обозначения:  – коэффициент загрузки системы

– интенсивность входног о потока,    – интенсивность обслуживания;

– второй начальный момент времени обслуживания;         – соответственно, дисперсии интервалов поступления и времени обслуживания,        – соответственно, среднее значение и второй начальный момент периода простоя.

Второе слагаемое в правой части (3) остается неизвестным, и вполне возможно, что оно может содержать моменты интервалов поступления и времени обслуживания более высокого порядка, чем первые два. Поэтому при анализе СМО G/G/1 (с произвольными законами поступления и обслуживания требований в системе) необходимо учитывать не только первые два момента случайных интервалов времен поступления и обслуживания, но и моменты более высокого порядка. И наконец, (1)-(3) убедительно демонстрируют зависимость основной характеристики СМО – среднего времени ожидания требований в очереди от вида входных распределений. Равенства (1)-(3) также можно интерпретировать как эволюцию СМО.

Анализ (3) показывает, что величина среднего времени ожидания требований в очереди связана

Постановка и решение задачи

В статье ставится задача исследования времени ожидания (3) для СМО G/G/1 на примере системы Н2/Н2/1, а также построения механизма аппроксимации произвольных законов распределений (G) с тяжелыми хвостами гиперэкспоненциальным распределением.

В настоящее время не существует аналитических методов для точного определения характеристик СМО G/G/1 или G/G/m, и как следствие, это отражается на степени адекватности стохастических сетевых моделей реальным компьютерным и телекоммуникационным сетям и на качестве принимаемых проектных решений.

В связи с тем, что система Н2/Н2/1 принадлежит классу систем G/G/1, ее точный анализ представляет собой актуальную задачу. При этом СМО с гиперэкспоненциальными входными распределениями в отличие от систем с распределениями с тяжелыми хвостами позволяет получить решение задачи в аналитическом виде. Тот факт, что такие распределения имеют место на практике, подтвержден в работе [2], где приведены результаты анализа интервалов между пакетами входящего трафика на сервер вуза.

В [3] авторами найдено преобразование Лапласа для функции плотности времени ожидания для системы Н2/Н2/1:

Ж*^ = ^(^PlX^Pl)

//^(s + sj^ + sj где Si и s2 – отрицательные вещественные части корней кубического уравнения

S3 -C2S2 -C^-Cg = 0.       (6)

c₀ - аД — а_хЪ_й — a₀ {p_x + Д₂) + 6₀ (A + Л₂),

Cj = -axbx -a0 -b0 + (Xx + Я2 )(//j + //2), а параметры: a0 = XxX^\ ax = pXx +(1 — p)X2;

А =//1Д₂; b_x =qp_x +(\-q^p₂-

Величины Pi ^1 7 ^2 ’ q ■> M\ ■> Pl являются параметрами гиперэкспоненциальных распределений с функциями плотностей

a(t)= pX_xe”^z'* +(1- p)X₂e~^^J;      (7)

b^ = qp_Ae~^Mx* + (1 - q^p₂e"^M- (8)

соответственно для системы Н2/Н2/1.

Среднее время ожидания в очереди равно значению производной от функции преобразования Лапласа (5) со знаком минус в точке s = 0. Окончательно среднее время ожидания в очереди для СМО Н₂/Н₂/1:

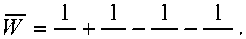
Si s₂ p_x p₂

Выражение (5) на основе свойств преобразования Лапласа, позволяет также определить моменты высших порядков для времени ожидания. Например, начальный момент 2-го порядка времени ожидания равен значению второй производной от преобразования (5) в точке s = 0 , и он будет иметь вид:

—_{2 =} d^4&l ₌       2    2(s₁₊s₂)

ds" P\Pi sxs2 pxp2s1xs2

x[s,s2(//i +//2)-//1//2(s] +s2)].

В свою очередь, начальный момент 2-го порядка позволяет определить дисперсию времени ожидания. Учитывая определение джиттера в телекоммуникациях как разброс времени ожидания от его среднего значения [4], тем самым получим возможность определения джиттера через дисперсию. Это является важным результатом для анализа трафика, чувствительного к задержкам.

Для практического применения результатов (9) и (10) необходимо определить входящие в них параметры. Определение этих неизвестных параметров рассматривается ниже.

Аппроксимация законов распределений на уровне двух первых моментов

Воспользуемся свойством преобразования Лапласа воспроизведения моментов и запишем начальные моменты до второго порядка для распределения (7):

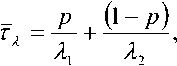
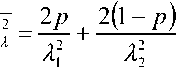
Рассматривая равенства (11) и (12) как уравнения метода моментов, найдем неизвестные параметры распределения (7) ^l 5 ^2 >  P . Для этого запишем связующее условие в виде выражения для квадрата коэффициента вариации

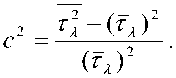
Заметим, что система уравнений (11) и (12) с тремя неизвестными является недоопределенной. Исходя из вида уравнения (10) положим

2, =1р!т_х,Х_г ^Ку-ру/т^ (14)

и потребуем выполнения условия (12). Подставив выражения (10)-(11) и (13) в (12) и решив квадратное уравнение относительно параметра p , пол учим для него два значения:

1 \ с, + 1

При этом можно воспользоваться любым из них [5].

Аналогично поступим с распределением (8). Следовательно, в [4] приведено частное решение недоопределенной системы уравнений (11)-(12), полученное методом подбора. Таким образом, гиперэкспоненциальный закон распределения может определяться полностью двумя первыми моментами и перекрывать весь диапазон изменения коэффициента вариации от 1 до ОО [5].

Рассмотрим пример. Пусть коэффициент загрузки СМО Р = ^, /^ =0,9; где Т X И 1 ц – средние значения интервалов между поступлениями и времени обслуживания. Рассмотрим случай нормированного обслуживания Тм=ц"х = \. Тогда средний интервал между поступлениями тл =10/9. Пусть коэффициенты вариаций случайных величин - интервалов между поступлениями и времени обслуживания СЛ С ц ^ . Аппроксимация на уровне двух первых моментов дает: р « 0,887 ; Я, » 1,597 ; Л ~ 0,203 ; q ~ 0,887 ; //, « 1,775 ; ц, « 0,225 . Таким образом, неизвестные параметры распределений (7) и (8) однозначно определены. Теперь воспользуемся результатом (8) для системы Н2/ Н2/1, приведенным выше. Коэффициенты кубического уравнения (6) в этом примере равны: с0 « 0,014 ; сх ~ 0,572; с2 - -0,20 . Найдем корни кубического уравнения (8) с помощью пакета Mathcad: -5, «-0,852; -s2 «-0,025; л3 « 0,677 . Тогда среднее время ожидания равно W « 36,20 .

Аппроксимация на уровне трех моментов

Учитывая тот факт, что распределение Н2 является трехпараметрическим, аппроксимацию можно выполнить и на уровне трех первых моментов, что позволит сравнить полученные результаты. С точки зрения теории вероятностей три момента полнее характеризуют случайную величину, поэтому такая аппроксимация будет точнее. Для этого запишем выражения для моментов 3-го порядка, полученные через преобразование Лапласа:

• -    для интервалов входного потока:

тт.бр бО-^ ⁺ цЗ ’

• -    для времени обслуживания:

2? _ бу 6(1- д)

^Т и 3 ⁺      3    ■

Цх ^2

.

Рассмотрим еще один пример: в рассмотренный выше расчет введем в качестве третьего момента коэффициент асимметрии и для определенности положим ^s л ^S д ^ . Как известно, для пуассоновского потока параметр A_s = 2. При тех же значениях входных параметров СМО начальные моменты 2-го и 3-го порядков для обоих распределений с оо тветственно будут равны: г; = 5 - (Ю/9)²; т\ = 45 - (10/9)³; ^=5;^=45.

При таких исходных данных для определения неизвестных параметров входных распределений

• (7) и (8): (2], Я₂, р\ (р_х ’ Аз ’ чХ запишем следующие системы уравнений на основе известного метода моментов:

Л+(Ы = 10/9

Х_х Я₇

2^2(1-77^5 (1()/9)2       (15)

^£+6(1-а) = 45.(10/9)з

. 21         Я32

решив которые, найдем искомые параметры. Решение системы (15) в пакете Mathcad после округления дает следующие результаты: р « 0,739, Я, « 3,306, Я₂ « 0,294.

д ! О-^) ^!;

Ai Аз ’ 2у 2(1-у)_ — +   2 - з,

Ai     Аз бу б(1-у)

3             3

1^1      д₂

Решение системы (16): у « 0,739; ц_х «3,673; //₂ «0,327. Тогда коэффициенты кубического уравнения (6) будут равны: с₀ « 0,130 ; с_х « 5,172 ; с_г « -0,40 , и его решение дает следующие корни: -5! «-2,471 , - $₂ « -0,025, 5₃ « 2,096. Воспользуемся результатом (9 ) и определим среднее время ожидания: W «37,051 . Относительная погрешность в сравнении с результатом аппроксимации на уровне двух моментов составляет 2,35%. При тех же условиях, но при коэффициентах асимметрии a_S2 = A_Sm = 10, получим среднее время ожидания W «34,537 .

Относительная погрешность при этом составляет 4,8%. Таким образом, учет моментов третьего порядка интервалов поступления и обслуживания показывает зависимость конечного результата (3) от моментов высших порядков. С точки зрения практического применения результатов СМО Н2/Н2/1, все же аппроксимация закона распределения на уровне двух первых моментов удобнее. Кроме этого, область допустимых значений относительно моментов 2-го и 3-го порядков для систем (15) и (16) при аппроксимации с использованием трех первых моментов может оказаться достаточно ограниченной.

Результаты проведенных вычислительных экспериментов и их анализ

С использованием выражений (9) и (10) проведены вычислительные эксперименты над временем ожидания (3).При этом использован достаточно широкий диапазон изменения параметров трафика, а именно: загрузки системы р от 0,1 до 0,9, а коэффициентов вариаций интервалов поступления и времени обслуживания ^с^с_м от 2 до 10. Это касается входных параметров. Выходными характеристиками являются: среднее время ожидания W, определенное по выражению (9) на уровне двух первых моментов интервалов поступления и обслуживания, дисперсия времени ожидания, определенное через (9) и (10), и в то рое слагаемое в правой части выражения (3) /² /(27) . Результаты экспериментов сведены в таблицу 1.

Анализ данных в таблице 1 подтверждает квадратичную зависимость времени ожидания (3) и (9) от коэффициентов вариаций интервалов поступления и времени обслуживания. Кроме того, время ожидания резко возрастает с ростом коэффициента загрузки р . Это говорит об адекватности полученного результата (9). Значения дисперсий времени ожидания /)„, позволяют находить разброс времени ожидания от его среднего значения (джиттер), например с использованием правила «трех сигма» Зег . И наконец, можно оценить поведение неизвестного второго слагаемого в выражении (3): оно также связано квадратичной зависимостью от коэффициентов вариаций интервалов поступления и времени обслуживания. Кроме этого, второе слагаемое убывает с ростом коэффициента загрузки р ■

Таблица 1. Результаты экспериментов

Входные параметры		Выходные характеристики
р	(сх,сА>	W	Dw	/2 /(2/)
0,1	(2,2)	0,45	3,7	26,50
	(4,4)	1,78	59,9	92,50
	(6,6)	4,0	303,7	202,50
	(8,8)	7,11	960,2	356,49
	(10,10)	11,11	2345	558,49

0,3	(2,2)	1,72	16,5	9,82
	(4,4)	6,88	265,4	35,81
	(6,6)	15,46	1346	79,14
	(8,8)	27,46	4258	139,80
	(10,10)	42,89	10400	233,23
0,5	(2,2)	4,04	47,69	6,46
	(4,4)	16,13	765,5	24,37
	(6,6)	36,16	3882	54,34
	(8,8)	64,18	12276	96,32
	(10,10)	100,19	29981	186,32
0,7	(2,2)	9,44	161,3	4,96
	(4,4)	37,72	2585	19,26
	(6,6)	84,53	13094	43,39
	(8,8)	149,95	41396	77,31
	(10,10)	233,99	101086	120,98
0,9	(2,2)	36,20	1583	4,08
	(4,4)	144,83	25340	16,11
	(6,6)	325,40	128294	36,66
	(8,8)	577.86	405483	65.75
	(10,10)	902.23	989966	103.38

Перейдем теперь к исследованию зависимости результатов (3) и (9) от моментов высших порядков. С учетом результатов п. 3 о зависимости конечного результата времени ожидания (3) для системы G/G/1 от моментов высших порядков проведем расчеты по установлению степени такой зависимости. В связи с тем, что время ожидания в данном случае будет зависеть от многих параметров трафика, отображение расчетных данных в одной таблице практически неосуществимо. Поэтому эти данные ниже будут представлены в текстовом виде.

Для этого рассмотрим случаи малой нагрузки ( р = 0,1), средней нагрузки ( р = 0,5) и высокой нагрузки ( р = 0,9). Расчеты, проведенные по методике п. 3, дают следующие результаты.

Время ожидания при мало й нагруз ке р = 0,1, при коэффициентах вариаций(с^с,,)= 2 и изменении коэффициентов асимметрии (Л, Л) от 4 до 15 варьирует от 0,72 до 0,32. ПриЛ,^С_А)=4 и изменении еллл от 7 до 15 варьирует от 4,82 до 1,50. При (с^с^ = 6 и изменении (Ах, лэ от 10 до 15 варьирует от 13,48 до 4,98.

При средней нагрузке р = 0,5; А/,^) = 2 и изменении (Ах, Л) от 4 до 15 время ожидания варьирует от 4,85 до 3,02. При (сл,с^ = 4 и изменении (Ах, 4ц) от 7 до 15 варьирует от 21,79 до 14,33.

При высокой нагрузке р = 0,9; (сл, ^СА = 2 и изменении (Ал, А.) от 4 до 15 время ожидания варьирует от 37,05 до 32,87. При (^сл,^сА = 4 и изменении (4x,4ц) от 7 до 15 время ожидания варьирует от 150,36 до 141,68. При Ал,с^ = 6 и изменении (Ал ’ 4/; ) от 10 до 15 время ожидания варьирует от 339,65 до 330,62.

Анализ последних данных показывает, что с ростом коэффициентов асимметрий при одной и той же нагрузке время ожидания уменьшается. Таким образом, влияние моментов высшего порядка на время ожидания в системе G/G/1 нельзя считать несущественным и им нельзя пренебрегать.