Исследование закритических деформаций пологих сферических панелей постоянной толщины

Тонкостенные оболочечные конструкции применяются в различных областях современной техники. В таких конструкциях под действием нагрузок могут возникать перемещения, не укладывающиеся в рамки линейной теории, что приводит к необходимости учета геометрической нелинейности [1–3]. Использование нелинейной теории позволяет определять напряженно-деформированное состояние (НДС) различного вида оболочек как в случае малых, так и больших прогибов. Однако с помощью этих уравнений значения критических нагрузок оказываются значительно больше значений, получаемых в результате экспериментов. Так, для сферических оболочек теоретически полученные значения критических нагрузок почти в 4 раза больше экспериментальных [4, 5]. Причин такого несовпадения результатов несколько. Это наличие у оболочки начальных неправильностей, начальных напряжений, отличие условий нагружения и закрепления от учитываемых в математической модели, неоднородность свойств материала, несимметричность деформирования и т. п. [4, 6]. Применение современных пакетов прикладных программ, основанных на методе конечных элементов [6], позволяет определять НДС и проводить сравнение с полученными решениями [7], но решение задач с высокой нелинейностью даже при использовании таких программ вызывает определенные трудности при получении решения. Таким образом, развитие методов расчета оболочек и учет их начальных несовершенств является актуальным и имеет важное прикладное значение.

Задача исследования сильного изгиба упругой оболочки вращения

Рассматривается геометрически нелинейная задача сильного изгиба тонкой изотропной оболочки вращения, в которой не накладывается никаких ограничений на величины углов поворота нормали к исходной координатной поверхности, а относительная линейная деформация мала по сравнению с единицей. Нагрузка, действующая на оболочку, осесимметричная.

Для оболочки, испытывающей осесимметричную деформацию, уравнения равновесия в координатах деформированной поверхности имеют вид [8]

d ( rN s )   _           Q

—---- - N _e cos ф + r ^s + rq = 0;

ds      °         Rs d ( rQs ) ds

—

( N N )

^r        r ⁺ rq z = 0;

l R s    R 0 J

d ( rM_s )    _           x

—^—- — M ° cos ф — rQ s — m s = 0.

Здесь Ns, Qs, Ms - продольные, поперечные силы и изгибающие моменты в меридиональном направлении, Nэ, Mo - усилия в окружном направлении, Rs, Ro - радиусы главных кривизн в мери диональном и окружном направлениях, r - радиус параллельного круга, s - длина дуги меридиана, qs - касательная и qz - нормальная составляющие распределенных нагрузок, ms - внешний распределенный момент. Тильдами сверху отмечены величины, относящиеся к деформированному состоянию оболочечного элемента.

Геометрические соотношения для оболочки в предположении осесимметричной деформации du

—- = s cos ф + cos ф — cos ф ;

ds s du

—- = s sin ф + sin ф — sin ф; ds s d 0 s _ d ф ds ds

d ф   _Z1 -         ё_

^—-г = ^{(1 +8} s ) х s ⁺ st ;

ds              Rs

_ ux ~  _ sin ф sin ф

0 =    ; X 0 =   2

rrr

^{X s} = R"

1 R s ^;

du w 1

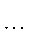
8„ =--+--+ - °v + s ds   Rs2

Здесь 8 _s , 8_e, x s , X₀ - относительные деформации удлинения и изменения кривизны срединной поверхности оболочки в меридиональном и окружном направлениях.

Соотношения упругости, связывающие усилия и моменты с компонентами полной деформации с учетом гипотезы недеформируемых нормалей, имеют вид:

^Ns = C 11 ^s s ⁺ C 12 ^S 0 ⁺ K 11 ^X s ⁺ K 12 ^X ° ; ^N 0 = C 21 ^s s ⁺ C 22 ^S 0 ⁺ K 21 ^X s ⁺ K 22 ^X ° ^;

5 = C 6₆ s s ° + 2 K 66 X s ° ;   M s = K 11 S s + K 12 S ° + d_ux s + D 12 X ° ;                        (3)

^M 0 = ^K 21 ^s s ^{+ K} 22 ^S 0 ⁺ D 21 ^X s ⁺ D 22 ^X ° ; H = ^K 66 ^s s 0 ⁺ D 66 ^X s 0 •

Здесь N_s, N _o, S - мембранные усилия, M s , M _o, H - изгибающие и крутящий моменты, 8 _{s o} - относительная деформация сдвига, x s _o - кручение координатной поверхности, C mp , K mp , D mp ( m, р = 1, 2) -коэффициенты упругости.

Для изотропных оболочек

Eh                   Eh               Eh

C ¹¹ = С ²² = 1 — V 2 ;  C ¹² = ^{V C11 ;}  С ⁶⁶ = 2(1 + v )^; D 11 = D ²² = 12 ( 1 — V 2 ) ;

D 12 = ^V D u;

Eh ³

⁶⁶   24 ( 1 + v ) ;

K 11 = K 12 = K 22 = K 66 = °,

где E - модуль упругости, v - коэффициент Пуассона, h - толщина оболочки.

Для получения разрешающей системы уравнений уравнения (1)–(3) необходимо дополнить граничными условиями.

Например, для жестко защемленного левого края и свободного правого u x = U_z = 0 _s = 0, при s = s 0 ,

N_x = N_z = M s = 0, при s = s_N .

Для решения задачи использовался метод Ньютона–Канторовича, сводящий нелинейную краевую задачу к итерационной последовательности линейных краевых задач. При решении линейных краевых задач применялся метод сведения их к ряду задач Коши, которые интегрировались численно методом Рунге–Кутта. Для обеспечения устойчивости решения жестких задач Коши применен метод дискретной ортогонализации С.К. Годунова.

Основные результаты

Исследовано напряженно-деформированное состояние пологих сферических панелей постоянной толщины с защемлением на внешнем контуре под действием равномерного внешнего давления (рис. 1).

Рис. 2. Схемы сферических оболочек

Рис. 1. Расчетная схема оболочки

Оболочки (рис. 2) имеют характеристики: модуль упругости E = 200 ГПа, коэффициент Пуассона ν = 0,3, толщина h = 1 мм, радиус опорного контура c = 100 мм. Образующие оболочек очерчены по окружностям, их параметры приведены в табл. 1. Параметр пологости [1] вычислял- c ся по формуле b = ^12(1 - v2)

Таблица 1

Параметры исследуемых оболочек

№	R , мм	Δ, мм	Параметр пологости b
1	516,5	0	8,00
2	543,84	–0,5	7,80
3	574,32	–1,0	7,59
4	608,51	–1,5	7,37
5	647,14	–2,0	7,15
6	491,85	0,5	8,20
7	469,51	1,0	8,39
8	449,17	1,5	8,58
9	430,59	2,0	8,76

На рис. 3 и 4 приведены кривые деформирования оболочек в координатах: внешнее давление – прогиб полюса при разных высотах ( H + Δ), где Δ = –2…2 мм. Номера кривых соответствуют строкам в табл. 1.

При уменьшении высоты оболочки происходит снижение внешней нагрузки в предельных точках, а при увеличении высоты оболочки значение внешнего давления в первой предельной точке существенно не изменяется.

Кривая 6 имеет петли, а на кривых 7, 8, 9 петли пропадают и остается одна предельная точка.

Для отыскания момента исчезновения петли получены две кривые, приведенные на рис. 5. Параметры оболочек, соответствующие этим кривым, приведены в табл. 2.

Таблица 2

Параметры оболочек

№	R , мм	Δ, мм	Параметр пологости b
1	501,41	0,3	8,12
2	496,58	0,4	8,16
3	480,41	0,75	8,29
4	479,97	0,76	8,30

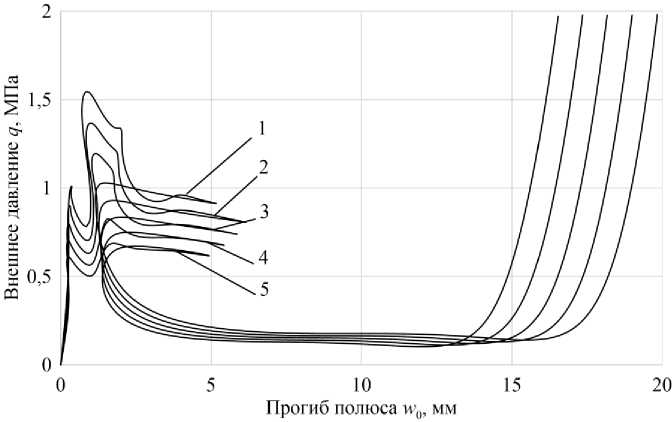
Рис. 3. Кривые деформирования оболочек

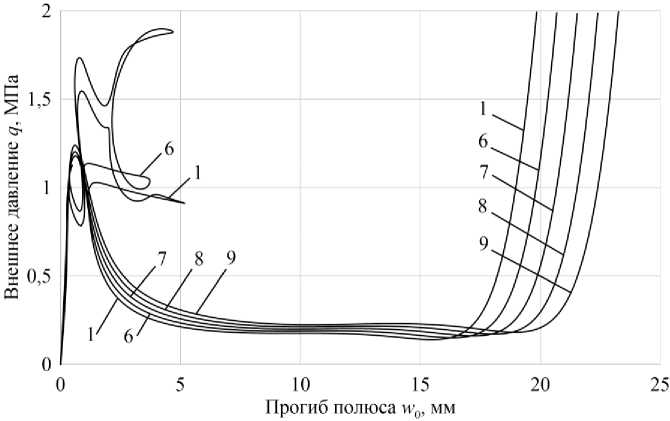
Рис. 4. Кривые деформирования оболочек

Рис. 5. Кривые деформирования оболочек

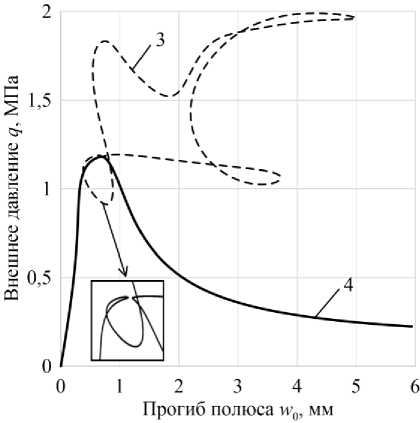
Рис. 6. Кривые деформирования оболочек

Чупин В.В., Черногубов Д.Е.

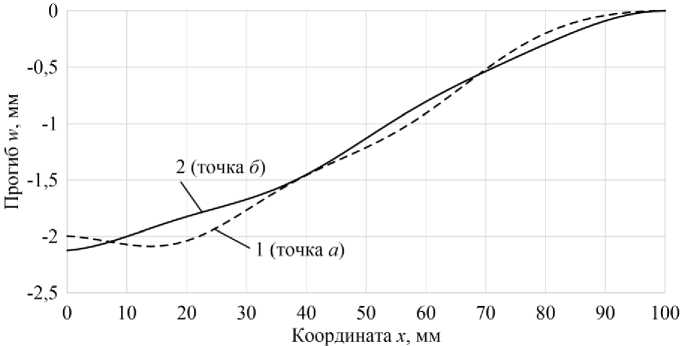
Рис. 7. Кривые прогибов

На рис. 7 приведены кривые прогибов оболочек для точек а , б (рис. 5). При переходе от точки а к б происходит «прощелкивание» четырех кольцевых поясов вдоль образующей оболочки.

Для определения момента исчезновения всех петель и перехода к кривой с одной предельной точкой получены две кривые, приведенные на рис. 6. Параметры оболочек, соответствующие этим кривым, приведены в табл. 2.

В окрестности первой предельной точки происходит смыкание двух ветвей петли, в результате получается гладкая кривая с одной предельной точкой.

Все расчеты выполнены по разработанной авторами программе, что подтверждает эффективность использованных алгоритмов.