Исследование зависимости эффективных податливостей плоскости с решеткой круговых отверстий от параметров решетки

Сейчас всё большее внимание привлекают материалы, содержащие наноструктуры пор, так называемые «сверхрешетки» — двоякопериодические системы отверстий, пор или каналов. Характерный диаметр полостей варьируется от нанометрового масштаба (цеолиты) до сотен нанометров (фотонные кристаллы, пористый кремний). Расстояние между полостями при этом, как правило, сравнимо с диаметром полостей.

Фотонный кристалл — материал, коэффициент преломления которого меняется периодически в пространственных направлениях. Известны фотонные кристаллы естественного происхождения как неорганического (некоторые разновидности опалов), так и органического (обнаружены на крыльях бабочек-парусников). Возможно создание фотонных кристаллов и искусственным путём, например протравливанием

периодической системы полостей в прозрачном для соответствующего излучения материале. Благодаря соизмеримости периода решетки с длиной волны излучения фотонные кристаллы обладают уникальными оптическими свойствами (во многом аналогичными полупроводниковым) и вследствие этого сегодня находят применение в различных областях, в частности в оптронике.

Пористый кремний впервые получен Артуром Улиром и Ингеборгой Улир (Arthur Uhlir Jr., Ingeborg Uhlir) в 1956 году. Он обладает рядом уникальных свойств, таких как фото- и электролюминесценция, низкая теплопроводность, широкий диапазон величин удельного сопротивления (10-2–1011 Ом∙см), а также способность к воспламенению и детонации в присутствии окислителя при определённых воздействиях. Все эти свойства — следствие наличия в пористом кремнии периодических систем отверстий, которые образуются в результате различных процессов обработки поверхности кремниевых пластин, обычно — травления.

Цеолиты — силикаты с нанопористой структурой, как природного происхождения, так и искусственно синтезированные (стильбит, клиноптилолит, морденит, фожазит, шабазит, хлоросодалит, натролит, пентасилы, VPI-5, МСМ-41 и другие), широко используются в химии каталитических, адсорбционных, ионно-обменных процессов, в том числе в крекинге нефтяных фракций, синтезе углеводородов, производстве моющих средств. Кристаллическая структура цеолитов образует периодические системы каналов субмолекулярного диаметра, благодаря чему цеолиты также называют молекулярными ситами, поскольку они обладают свойством пропускать или адсорбировать только определенные вещества.

Многочисленные приложения перечисленных материалов к технологическим процессам требуют детального изучения их механических свойств. Уникальные качества нанопористых материалов обуславливаются их внутренней структурой и при ее разрушении значительно ухудшаются или вовсе исчезают. Соответственно, важную роль приобретает правильная оценка напряжённо-деформированного состояния, возникающего под действием тех или иных нагрузок. В частности, особое значение имеет корректный расчёт эффективных упругих характеристик материала; известен феномен их анизотропии.

Ряд характерных особенностей механического поведения таких материалов можно описать в рамках плоской задачи теории упругости, рассматривая их в виде плоскости, ослабленной двоякопериодической системой отверстий. Известно, что двоякопериодические структуры обладают ярко выраженной анизотропией свойств, в том числе и упругих, а эффективные упругие характеристики решетки могут существенно отличаться от упругих характеристик матрицы.

Поле напряжений, создаваемое одиночным круговым отверстием в упругой плоскости при произвольном нагружении, хорошо изучено. Известно точное аналитическое решение (см., например [1, 2]) такой задачи при произвольной нагрузке на контуре отверстия и на бесконечности. Это решение может быть применено к материалу при достаточно редко расположенных в материале порах. Однако при характерном расстоянии между отверстиями, сравнимом с их диаметром (именно такой материал рассматривается в настоящей работе), влияние отверстий друг на друга вносит значительные искажения в поля напряжений.

Уже для двух круговых отверстий аналитическое решение представляет серьезную проблему. Кроме того, наличие решетки отверстий порождает свои сложности, такие как необходимость использования ζ-функции Римана в интегральных ядрах сингулярных граничных интегральных уравнений [3]. Изучению задачи расчета напряжений для плоскости с периодически и двоякопериодически расположенными отверстиями или включениями (группами отверстий или включений) и определению эффективных упругих характеристик большое внимание уделено в работе [4].

В [ 5 ] для расчета напряженно-деформированного состояния плоскости с круговыми отверстиями предложен метод мультипольных разложений. Особенность этого метода состоит в том, что решение задачи ищется в виде комбинации мультиполей — элементарных упругих полей деформаций, создаваемых точечными дефектами различной структуры. Каждый член разложения имеет конкретный физический смысл и отражает вклад в общее поле той или иной элементарной деформации. Развитию метода мультипольных разложений для случая системы сферических пор в упругом континууме посвящена работа [ 6 ].

В данной работе метод мультипольных разложений предлагается продолжить на решение задачи определения эффективных упругих характеристик материала упругой плоскости с двоякопериодической решёткой. Будет исследована зависимость эффективных податливостей и коэффициента Пуассона от расстояния между отверстиями решётки и направления приложенных нагрузок (для случая квадратной решётки) и продемонстрирована их анизотропия; выявлено существование значений эффективного коэффициента Пуассона больших 1/2 (подобные эффекты известны для некоторых анизотропных материалов, см. например [ 7 –9 ]); отмечено возникновение продольных деформаций при приложении касательных нагрузок и, наоборот, сдвиговых деформаций при нормальных нагрузках.

• 2.    Постановка задачи

• 3.    Основные положения

Рассматривается бесконечная упругая плоскость, содержащая систему одинаковых круговых отверстий L l,m радиуса R (в данной работе радиус полагается единичным) (Рис. 1). Центры отверстий образуют двоякопериодическую решетку с произвольными

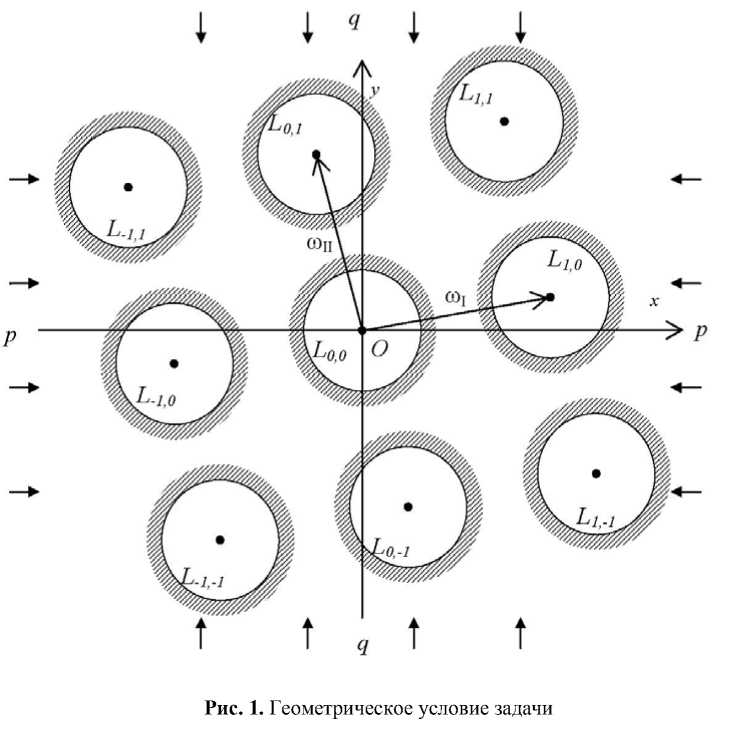
Рис. 1. Геометрическое условие задачи периодами «I и юц. Нагрузка на контурах отверстий отсутствует. Требуется найти эффективные упругие характеристики среды (связь средних напряжений с эффективными деформациями) и исследовать их зависимость от геометрических параметров решётки.

В [ 5 ] изложен метод мультипольных разложений в применении к задаче с двумя отверстиями в упругой плоскости. Метод основан на теории комплексных потенциалов Колосова-Мусхелишвили, и его суть состоит в том, что функция смещения g’ ( t ) на каждом из контуров представляется в виде суммы мультиполей:

да

g'(t )= Е gnt", n=-да где t — комплексная локальная координата точки на контуре. Тогда сингулярное граничное интегральное уравнение может быть преобразовано в систему линейных уравнений относительно комплексных коэффициентов разложения (набор которых однозначно описывает напряжённо-деформированное состояние плоскости).

Действуя по аналогии с [ 5 ] и используя свойства симметрии решётки, можно показать, что для определения коэффициентов разложения g _n получается следующая система уравнений:

g 2 к - 1 = °,      k ^G Z ;

да

- 2 g о + 2 ЕЕ "

n = 1 l , m

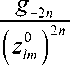
ГГ "  ^g -2 n

Ze Ze / _° \2 n n = 1 l , m | Zi 1 lm

p + q .

i 2 ;

.W-   ^{g 2} n

^ЕЕ / _° \2( n + 1) n = 1 l , m I Z, 1 lm

4 у''

i^o l,m

⁺ g - 2

-2ZZ          2 ” 'Izm (-(n+1)(2 n+1)1 =ip-q n=1 l,m I Z, I                                                        -I 2

lm

g„      ( 2 ( к + n ) - 1 ) !

^{g 2} k ⁺ 2 ^ЕЕ" ( Z m J^^^+ n ⁷ ( 2 к ) ! ( 2 n - 1 ) ! = °’ k > ¹

да g-2 к - 21Е ” g 2 n n=1 l, m

1       ^{( 2 ( k +} n ^{)- 1 ) !} - _4V.„ 2 к - 1

( z m f^{1 + n )}( ^{2 k} - ² ) ' ( ² n + * ) '    ¹¹ g ° ( z m )^{! k}

да

- 2 ЕЕ '' g - 2

n = 1 l , m

- ° \^{2( 1 + n} ) z lm )

( 2 ( к + n ) - 2 ) ! । ° p ( 2 к + 2 n ) ! ( 2 к - 2 ) ! ( 2 n - 1 ) ! ‘I z lm l - ( 2 к ) ! ( 2 n ) !

= °,

(6) к >  2.

Здесь z lm = l ‘ ro I + m ‘ ro_n — координаты центров отверстий; к — целое число;

Z — множество целых чисел; знак Е " обозначает суммирование по всем парам индексов l , m

(l = °, m = 1 . +да) и (l = 1 . +да, m = -да . +да) (таким образом, учитывается ровно половина слагаемых, причем среди них нет противоположных пар); надчеркивание показывает комплексное сопряжение.

Свободный член системы содержит величины p и q , в [ 5 ] имеющие смысл главных напряжений на бесконечности. Но в случае периодической решетки на бесконечности отсутствует сплошная среда, а следовательно, и однородное напряженное поле. Отсюда вытекает, что напряжения, заданные на бесконечности, в такой постановке не имеют смысла. Однако для периодической решетки можно говорить о средних по периоду напряжениях. Таким образом, в рассматриваемой задаче необходимо подобрать величины p и q так, чтобы средние по каждому из периодов напряжения имели требуемые значения. Это можно сделать, воспользовавшись принципом суперпозиции.

Сначала решим систему (2)–(6) отдельно для каждого вида элементарного (единичного) нагружения: горизонтального растяжения, вертикального растяжения, сдвига (поворота решетки на 45 ° ). Найдя в каждом случае средние по периодам напряжения, вычислим их линейную комбинацию, которая даст необходимые значения.

По определению эффективные податливости периодической системы связывают средние деформации со средними напряжениями:

е„ = Sy 6 I .                                                                                   (7)

ij ijkl kl

Отсюда видно, что податливость Sy_kl равна деформационному отклику £ _у на единичное воздействие 6 _kl при остальных равных нулю напряжениях (в частности это означает, что задачу нужно решать при плоском напряженном состоянии: κ = (3 – ν)/(1 + ν), где ν — коэффициент Пуассона). Согласно [ 3 ] для задачи со свободными от нагрузок контурами выполняются следующие соотношения:

А/

А/

^{+ 6} 22

= S Im J и ( t ) dt +" E ” ( 6 11 + 6 ₂₂ ) = S Im J и ( t ) dt + 2 -~- 6 ;

Л/

^{- 6} 22

+ 2 i б ₁₂

i f / X . 1 +

= — I и ( t ) dt +--

SLE

⁶ 22 ^{+ 2} i ⁶ 12 ) = -i J u ( t ) ^{dt + 21 +V} ( ^{5 +} i ^T ) .    ⁽⁹⁾

S L E

Здесь S = Im ( o , •to II) — площадь основного параллелограмма решетки; L — контур отверстия (индексы опущены, так как интегралы не зависят от них); i — мнимая единица. Поскольку величина смещений u ( t ) вычисляется через функцию смещений g ( t ) (см. [5]), то записав

J и ( t ) dt = i 12^ J g ( t ) dt = E J g ( t ) dt = E • ^{2 n} i g - 2 = - E g - 2 , r,.      4 i p _z         4 i f , ddt 4 i _          8 n

J u ( t ) dt = —J g ( t) dt =- —J g ( t) -г = —•2n zgо =- — go, LELELtEE получим:

/4/               /4/

⁶ 11 ^{+ 6} 22 _

1 -v„ 4 n _T

— ^6--^7 ^Im g 0 ,

E ES

z*z               z*z

⁶ 11 ^{- 6} 22

1 + v

E

^

4n T

Im g - 2 , ES

A*

^£ 12

1 + v_ 4 n

----т--Re g .•

E ES ²

В формулах (10)–(14) приняты обозначения: E и G — модуль упругости и модуль сдвига; с , s, т — компоненты средних напряжений в решетке.

Отсюда следует, что средние деформации складываются из двух частей. Первое слагаемое соответствует однородной деформации сплошной плоскости под воздействием напряжений, равных средним с , ; т . Второе слагаемое — это поправка, которую привносит наличие отверстий. Отметим, что поправка определяется всего лишь двумя членами мультипольного разложения. Причем поправка к средней объемной деформации определяется членом Im g 0 , описывающим всестороннее растяжение/сжатие контура, поправки же к сдвиговым компонентам средней деформации обуславливается членом g -2 , описывающим деформацию чистого сдвига контура.

Исходя из принципа суперпозиции, представим члены мультипольного разложения как линейные комбинации 3 , s, т :

g k = g k " + g k s + g k ~ •

Подставив эти комбинации в выражения для средних деформаций, получим

A* ^£ 11

, ~   _ Io ^{1 - v}

^{+ ;} 22 = I ²

k E

8п _т с

ES Im ^g 0

•3-

^8п T s ~   ^8п T т ~

---Im g ₀ • s --Im g ₀ •т ,

ES ⁰ ES ⁰

A* ^£ 11

8 ” _c I 1 + v

8₂₂ =--- Im g - •" + 2----

²² ES ² I E

8n T         I . 8n т _ T ~

— Im g₂ • s + — Im g ₂•т ,

ES ² ) ES ²

A*

^£ 12

—- Re g " •d

ES ²

4n n

Re g ^s

ES ²

_ 11 + v 4n_ _T 1 _

• s + Re g i гт • k E ES ² J

Здесь

3 =

z*z                 z*z

311 + 322 .  ~ _

;   s =

z*z                 z*z с11 -c

;

22   ~   _

—; т = с

12 — компоненты средних напряжений в решётке;

g ³ s , ^т g_n

— коэффициенты разложения, вычисленные для соответствующих единичных средних напряжений (–∞ < n < +∞).

Эффективные податливости определяются соотношением (7), с учетом которого запишем:

^S 1122 = 41 ^{-v +} 2 ? ( ^Im g -^C 2 ^{- Im} g 0 ^{- Im} g - 2 ^{+ Im} g 0 s ) E k S

^S 1112 = ^S 1121 = |^П ( ^Im g - 2 ^{- Im} g 0 ) ,

ES

^S 2211 = 4^|-v- 2 ^П ( ^Im g ^C 2 ^{+ Im} g б " ^{+ Im} g - 2 ^{+ Im} g 0 ) E k S

^S2222 = -¹1 ^{1 -} 2 7 ( Im g -^C 2 ^{- Im} g - 2 ^{+ Im} g о " ^{- Im} g 0 ) | ,

E k S                              ⁷J

^S 1211 = ^S 2111 = es ( ^Re g - 2 + ^Re g - 2 ) ,

^S 1222 = ^S 2122 = - ES " ( ^Re g - 2 - Re g - 2 ) ,

1212      1221

2112     2121

1 ( 1+v

E (~"2"~

2 n

S ^Re g - 2

Полученные формулы использованы далее для расчета эффективных податливостей.

• 4.    Зависимость эффективных податливостей от периода решётки

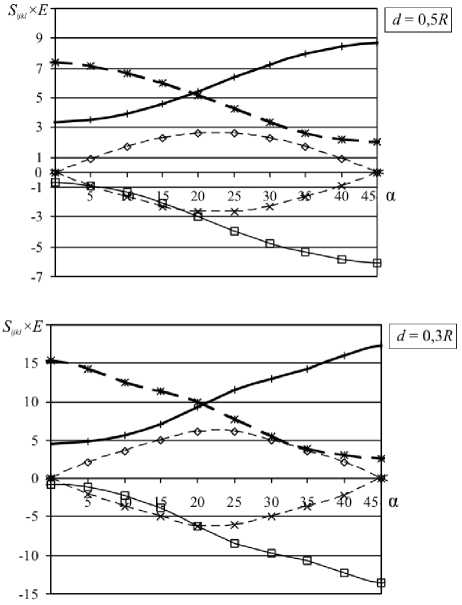
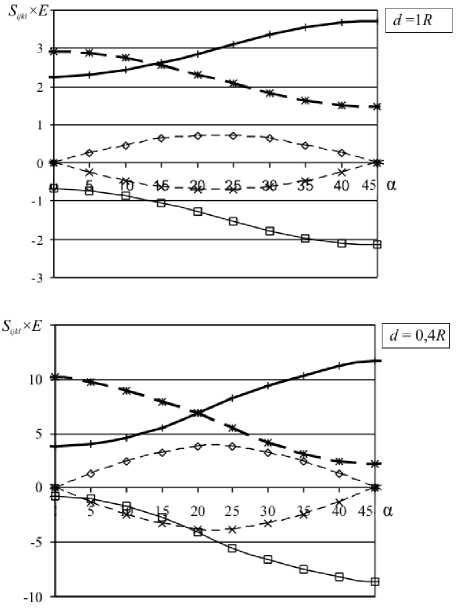
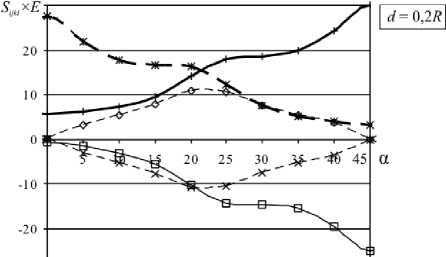
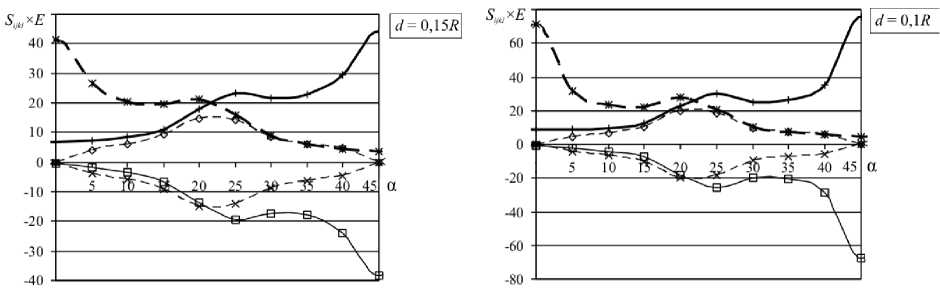
Были рассчитаны значения эффективных податливостей для различных углов ориентации (α = arg ω I ) квадратной решётки (ω II = i ω I ). В силу симметрии задачи рассмотрены углы ориентации от 0 до 45 ° включительно. Результаты расчётов представлены на рисунке 2.

Далее, для удобства введём характеристику квадратной решетки, называемую расстоянием между соседними отверстиями: d = |ω I |-2 R . Отметим, что при d , равном десяти радиусам и более, анизотропия в распределении эффективных податливостей практически не проявляется. При уменьшении расстояния анизотропия начинает проявлять себя в том, что характер распределения становится синусоидальным с экстремумами при углах ориентации 0 ° и 45 ° , или же при 22,5 ° (для «смешанных» податливостей типа S 1112 ). При дальнейшем сближении отверстий синусоидальный характер распределения нарушается, появляется локальный максимум в области « 25-28 ° ( « 17-20 ° для S 1212 ) и локальный минимум в области « 28-33 ° ( « 12-17 ° для S ₁₂₁₂). У «смешанных» податливостей экстремум при 22,5 ° становится более отчётливым.

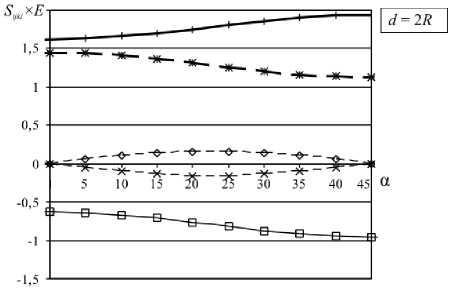
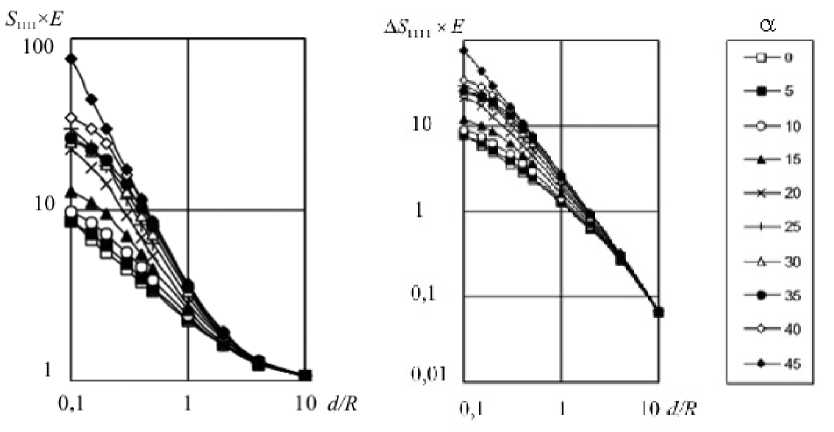
На рисунке 3 представлены зависимости податливости на продольное растяжение S ini и разницы A S цц между S цц и податливостью матрицы от расстояния между отверстиями для различных ориентаций решётки. Очевидно, что с увеличением расстояния податливость будет стремиться к единице, то есть к податливости матрицы. Поэтому больший интерес представляет поведение разницы A S 1111 . Из графика в двойных логарифмических координатах (Рис. 3, б) можно видеть, что зависимость A S ₁₁₁₁( d) стремится к степенной функции A S ₁₁₁₁( d ) « E ^л3,22^ d ^-1,67. Наиболее близко к этой функции поведение податливости при диагональной ориентации решётки (при 45 ° ).

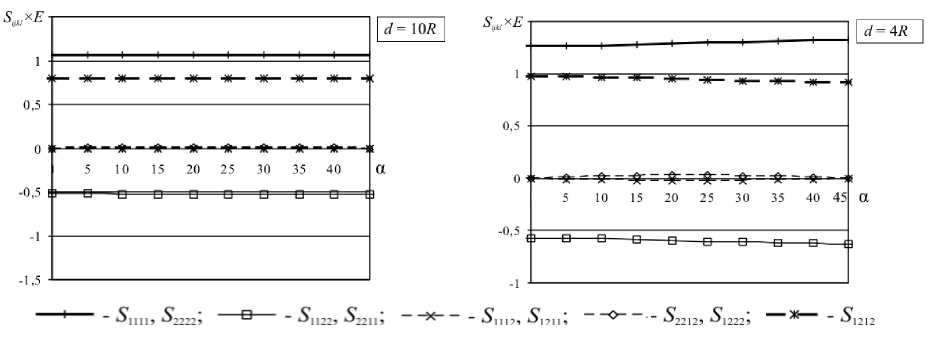
Рис. 2. Зависимость эффективной податливости решётки S ijkl от угла поворота решетки α (град) при различных значениях расстояния между отверстиями

■30

а

б

Рис. 3. Зависимость S 1111 ( а ) и A S 1111 ( б) от расстояния между отверстиями для различных ориентаций решётки а (град)

• 5.    Зависимость эффективного коэффициента Пуассона от периода решётки

  Представляет интерес эффективный коэффициент Пуассона ν eff = – S 1122 / S 1111 и его зависимость от коэффициента Пуассона матрицы ν. Значения ν eff при различных ν для разной геометрии решётки представлены на рисунке 4.

Отметим, что эффективный коэффициент Пуассона демонстрирует поведение, аналогичное поведению S 1111 . При d > 10 R анизотропия практически не проявляется, ν eff постоянен и близок к ν матрицы. С уменьшением расстояния анизотропия обнаруживает себя синусоидальной зависимостью от ориентации решётки. Как только начинает выполняться условие d < 0,5 R , синусоидальный характер нарушается, появляется локальный максимум при ориентации « 24-26 ° и локальный минимум при ориентации « 33 ° . Уменьшение расстояния d снижает влияние коэффициента Пуассона матрицы ν; разброс значений уменьшается (особенно для диагонального расположения решётки), так что значение ν eff начинает в подавляющей степени определяться ориентацией решётки.

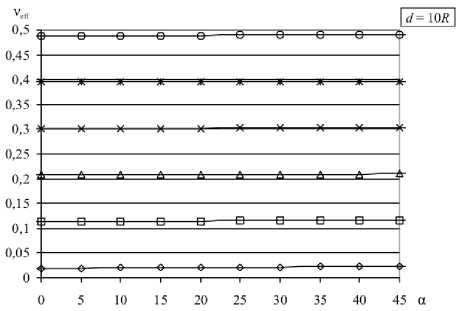
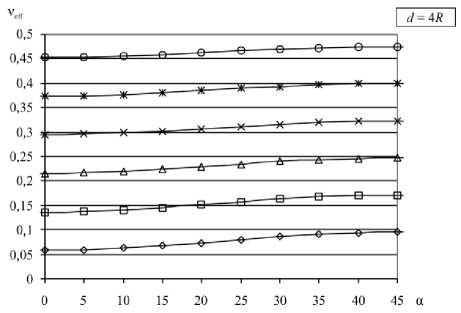
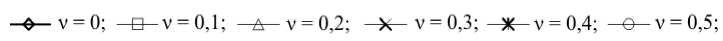
Рис. 4. . Эффективный коэффициент Пуассона решётки ν_eff в зависимости от угла ориентации α (град) при различных значениях коэффициента Пуассона матрицы ν

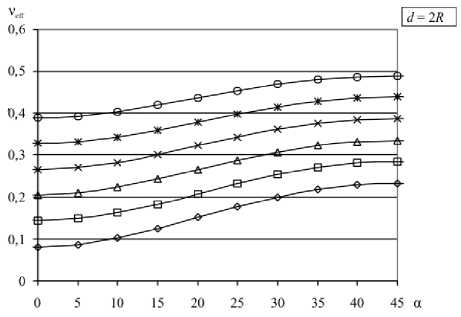
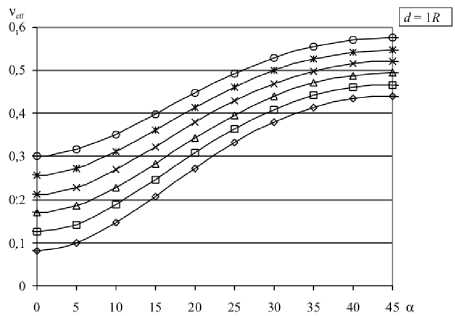
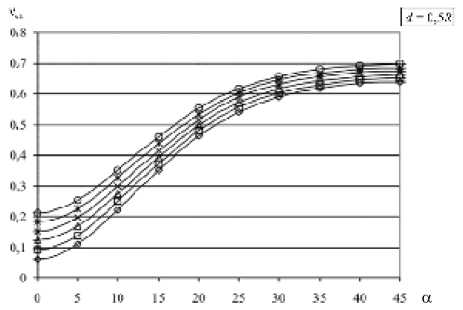
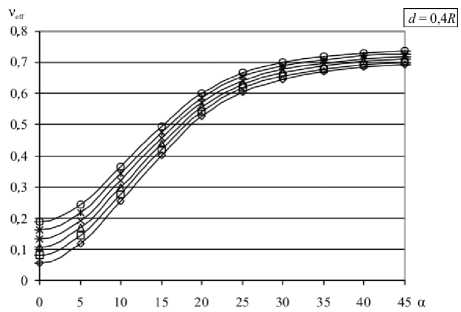
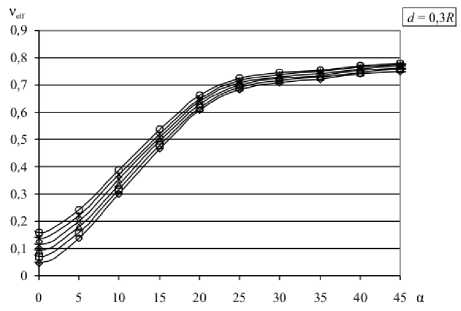
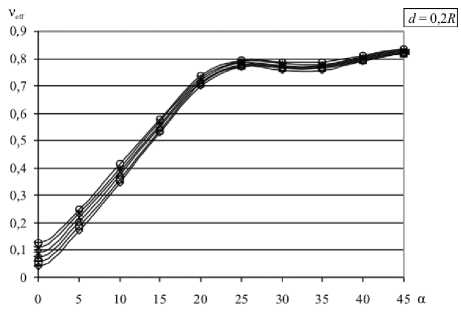
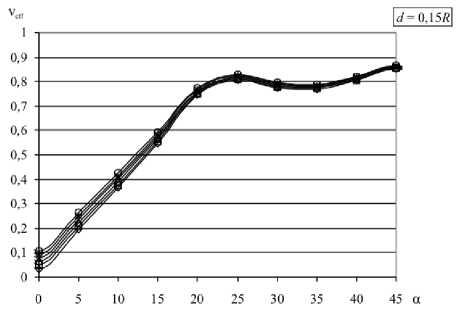
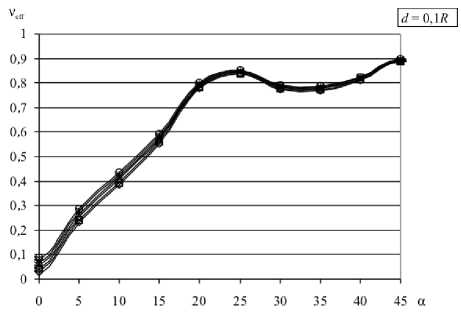
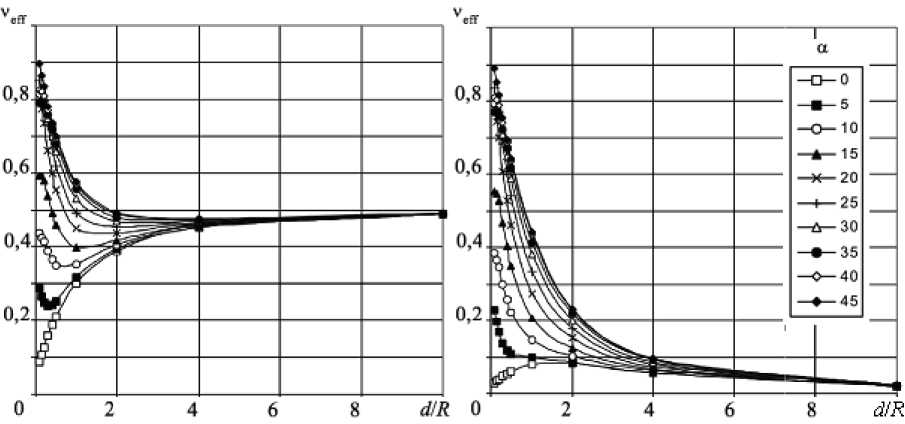
Рис. 5. Зависимость v eff от расстояния между отверстиями для значений коэффициента Пуассона матрицы v = 0,5 ( а ) и v = 0 ( б) и различных ориентаций решётки а (град):

На рисунке 5 представлены графики зависимостей ν eff от расстояния между отверстиями для коэффициентов Пуассона матрицы равных 0,5 и 0 соответственно. Из графиков видно, что зависимости могут иметь довольно сложный характер. Так, например, в случае ν = 0,5 эффективный коэффициент Пуассона при уменьшении расстояния d сначала уменьшается, затем, достигая минимума при соотношении d/R от 0 до 4, начинает расти (за исключением ориентации решётки 0 ° ). Таким образом, если известно направление прилагаемых к решётке нагрузок, то становится возможным вычисление геометрических характеристик системы, при которых поперечная деформация при продольном растяжении/сжатии будет минимально возможной.

Нельзя не отметить, что при d <  2 R существуют широкие области значений ориентации решётки, для которых ν eff превышает максимальное для изотропных материалов значение 0,5. Подобное поведение известно для некоторых анизотропных материалов. В работах [ 7 – 9 ] приведён обзор ряда веществ с аномальными значениями эффективного коэффициента Пуассона (ν eff > 0,5 или ν eff < 0), а также дается теоретическое обоснование данного эффекта. В частности показано, что причиной аномалии является структурная особенность кристаллической решётки данных материалов.

• 6.    Заключение

В представленной работе исследовано поведение эффективных податливостей и эффективного коэффициента Пуассона упругой плоскости с двоякопериодической системой круговых отверстий.

Продемонстрирована анизотропия эффективных упругих характеристик. Выделены три области значений отношения d/R , в которых характер анизотропии существенно различается. В области d/R > 10 анизотропия почти не проявляется (хотя эффективные упругие характеристики уже могут заметно отличаться от характеристик матрицы). При 0,5 <  d/R < 10 анизотропия носит выраженный синусоидальный характер. В случае d/R < 0,5 синусоидальный характер нарушается и, если ориентация решётки отлична от продольной (0 ° ) и диагональной (45 ° ), появляются локальные экстремумы.

Исследована разница между эффективной продольной податливостью и продольной податливостью матрицы, выявлен степенной характер зависимости этой разницы от отношения d/R .

Продемонстрировано снижение влияния коэффициента Пуассона матрицы на эффективный коэффициент Пуассона: при уменьшении расстояния между отверстиями величина ν eff в подавляющей степени определяется выбранной ориентацией решётки. При этом диапазон значений углов ориентации, в котором ν eff > 0,5, довольно широк. Подобные аномально высокие значения эффективного коэффициента невозможны для изотропных сред, но обнаружены для некоторых анизотропных материалов.

Дальнейшее развитие темы возможно, в частности, в направлении распространения задачи на упругое пространство с использованием метода мультипольного разложения для трёхмерного случая [ 6 ].

Автор выражает благодарность члену-корреспонденту РАН Р.В. Гольдштейну за ценные обсуждения и рекомендации.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 08-01-00696).