Исследование жёсткости зубьев двух и трёх парного зацепления

возбуждения изделия не будет происходить. При синусоидальной зависимости - С = sin( πх /2) или по квадратичной параболе - С = х² параметрическое возбуждение может происходить с максимальным значением суммарной жесткости - С посредине шага зацепления. А вот при зависимости по кубической синусоиде - С = sin³( πх /2) параметрическое возбуждение так же возможно, но уже с максимальным значением суммарной жесткости – C не посредине шага зацепления, а в начале и конце каждого шага зацепления. Для исследования действительного характера изменения суммарной жесткости зубьев зубчатых колес были построены профиля зубьев методом конечных элементов по программам ANSYS – рис.2. Один профиль строился по ГОСТу, а другой несколько удлиненным по высоте. Модуль зацепления – m = 4,6 мм (как в исследуемом [1] дифференциальном редукторе турбовинтового двигателя). Угол исходного профиля -20⁰. Результаты расчетов удельных жесткостей в зацеплениях зубьев приведены в таблицах ниже и на рис.3. Расчетные значения для удельных жесткостей одной пары зубьев хорошо согласуются с экспериментальными данными, приведенными в технической литературе.

В дальнейших расчетах для удельных жесткостей пары сопряженных зубьев нами были приняты следующие значения: в середине зацепления (в полюсе) – C_O = 18000 Н /мм², а в начале и конце зацепления – C_k =12500 Н /мм². Как видно по результатам исследований, изменение жесткостей зубьев в процессе зацепления имеют нелинейный характер как в области одно парного, так и в области двух парного зацеплений.

Таким образом, и при полностью двух - парном зацеплении и при трех - парном зацеплении зубчатых колес также будет происходить параметрическое возбуждение упругих систем,

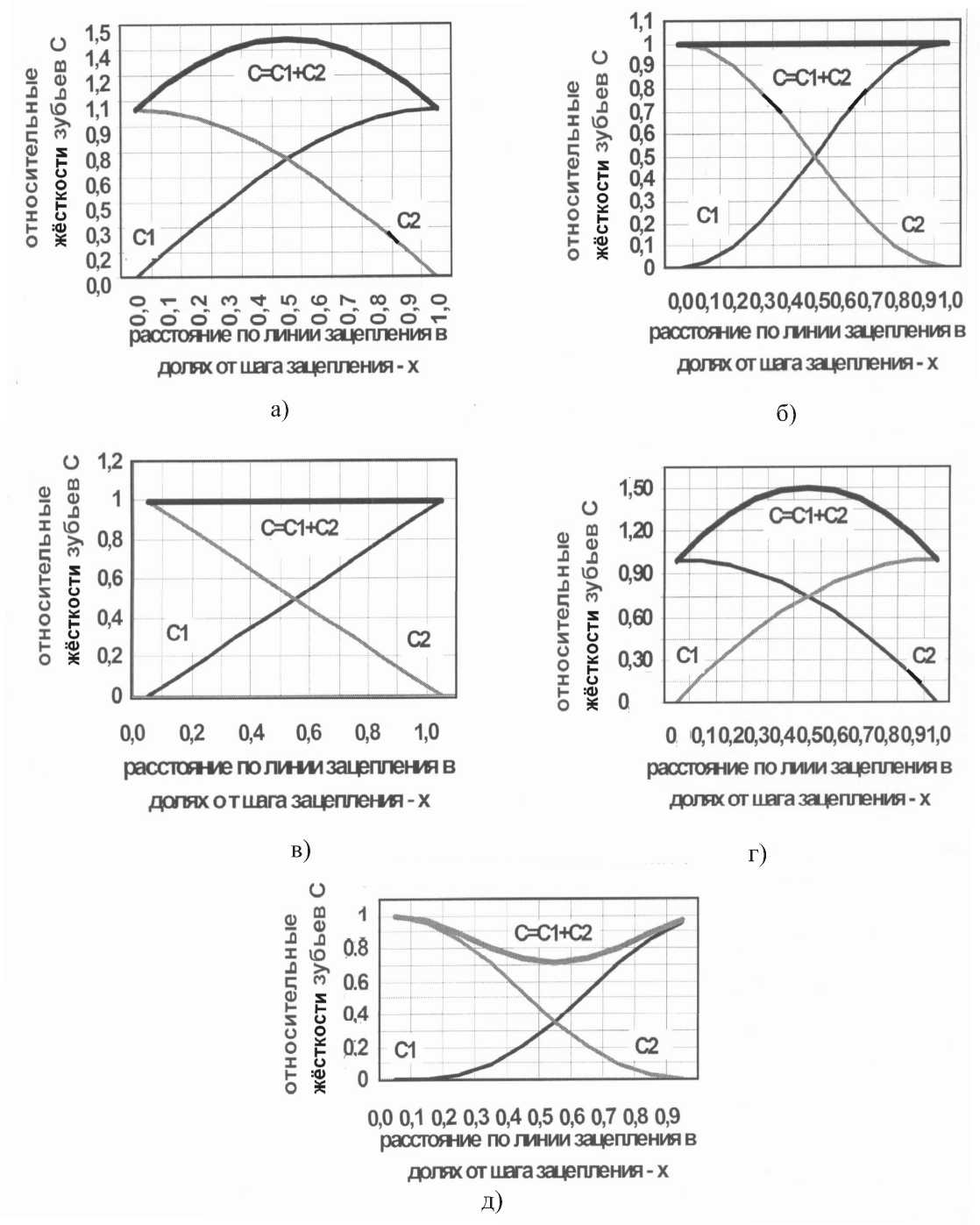
Рис. 1. Варианты изменения суммарных жесткостей зубьев в зацеплении - С = С 1 +С 2 на возможность параметрического возбуждения в зависимости от характера изменения жесткостей зубьев входящих в зацепление - С 1 и выходящих из зацепления С₂ в различных точках - х по линии зацепления в пределах одного шага зацепления: а - С = sin( пх /2); в - С = sin²( пх /2); в - С = х; г - С = х²; д - С = sin³( пх /2)

в которые они входят. Но все же, по сравнению с одно - двух парным зацеплением разница большая. Во - первых, при полностью двух парном зацеплении жесткости в зацеплении в среднем в два раза больше, чем при одно парном зацеплении. Во - вторых, и это очень важно, амплитуды изменения жесткостей в среднем так же в два раза меньше, чем при одно- двух парном зацеплении. В - третьих, при двух-трех парном зацеплении изменение жесткости в зацепления каждого зуба циклически повторяется два раза. При численных решениях дифференциальных уравнений пара-

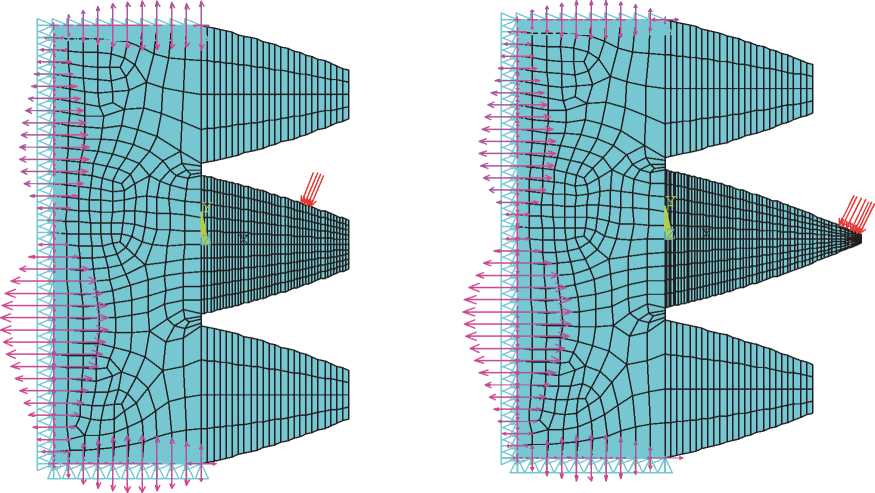
Рис. 2. Два варианта профилей зубьев для исследования жесткостей методом конечных элементов по программам ANSYS:

о дин профиль (левый) - по ГОСТу, другой (правый) - несколько удлиненным по высоте.

Модуль зацепления – m = 4,6 мм (как в исследуемом дифференциальном редукторе турбовинтового двигателя).

Угол исходного профиля -20o

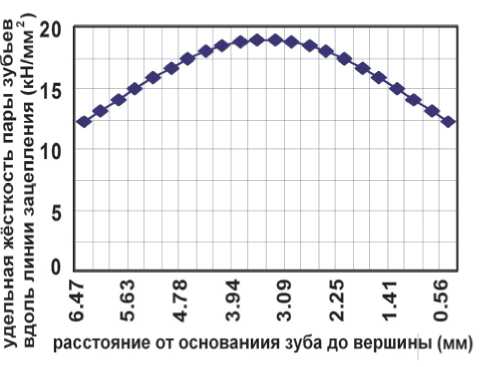
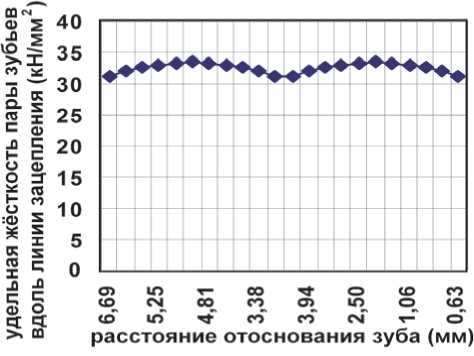
а)                                                               б)

Рис. 3. Удельные жесткости в зацеплениях зубьев шестерен при двух парном зацеплении вдоль линии зацепления (два основных шага): а – для одной пары зубьев; б – для двух пар зубьев метрической динамики упругой системы нужно иметь аналитические зависимости изменения жесткостей зубьев в процессе зацепления. По опытным данным и при исследованиях методом конечных элементов можно принять, что эта зависимость близка к квадратичной параболе или к синусоиде – максимальное значение жесткости одной пары контактирующих зубьев находится в середине линии зацепления – CO , как показано на рис. 4, а минимальное в начале и конце зацепления - CK . При двух парном зацеплении они складываются (суммируются) до значений двух парного зацепления – Cd .

На рис. 5 приведены графики изменения жесткостей зубьев в процессе одно- двух парного, двух- трех парного и, даже, трех- четырех парного вариантов зацепления зубчатых колес. Видно, как складываются жесткости зубьев в процессе зацепления их. Выведем сначала зависимости для жесткости параболического типа. По внешнему виду этих графиков, полагая, например, что жесткость одной пары зубьев изменяется по параболической зависимости - С = a • x2 + b • x + d из условия равенства ее в характерных трех точках можно определить значения коэффициентов -a,b,d . Необходимо, что бы было: в начале шага по линии зацепления, при x = 0 - С = CK, в середине длины активной линии зацепления при x = (^ • p) / 2 - С = CO, а в конце активной части

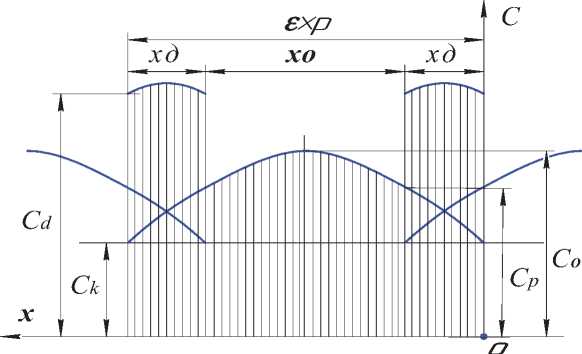
Рис. 4. Изменение жесткости по линии зацепления одной пары зубьев

линии зацепления при x = ( s • p ) - C = C K . Подставляя эти значения в уравнения параболы и решая алгебраическую систему трех уравнений, находим значения коэффициентов a, b, d . Таким образом, получаем аналитическую зависимость параболического типа для определения жесткости одной пары зубьев в зависимости от положения - x места контакта зубьев по линии зацепления ^- C = C p + ⁴ • ⁽ C o - C_K ) •[ x /^{( s} • p ^{) ]}- [ l - x/ ( £• p ^{) ]} .

Здесь, напомним, s - коэффициент перекрытия, а p - основной шаг зацепления. Координата x определяется по зависимости - x = (У • ro, где <у - угловая скорость ведущего колеса, в том числе и с учетом вибраций, а ro - радиус основной окружности ведущего колеса.

Эта зависимость, хотя и не полностью, действует в области зацепления одной пары зубьев - рис. 5 а). В области же двух парного зацепления жесткости определяются (складываются) по такой же зависимости еще и от предыдущей пары зубьев, но только смещенной на один шаг влево - рис. 5 а) - C 2 = C k + 4 • ( C o - C k ) • [ ( p + x )Ks- P ) ] - [ 1 — ( P + x )Ks- P ) ]

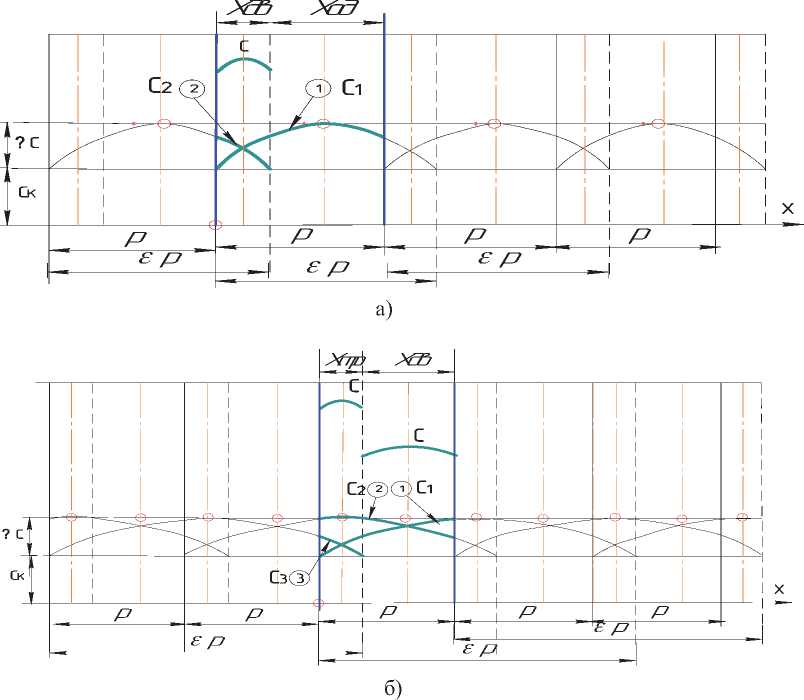
Рис. 5. Изменения жесткостей зубьев в процессе зацепления для различных вариантов исполнения зубчатых колес: а – одно – двух парное зацепление; б – двух – трех парное зацепление

и таким образом, в области двух парного зацепления действует суммарная жесткость двух пар зубьев - С = С + С ₂ .

Аналогично получим аналитическую аппроксимацию жесткости зубьев синусоидального характера. Так для случая одно- двух парного зацепления получим, обозначив - А С = С О - С : в области одно парного зацепления - C₁ = C P +А С ■ sin [ П ( e pх ) ] , а в области двух парного зацепления еще добавиться смещенная влево - рис.5 а) жесткость предыдущей пары зубьев- C ₂ = C k + А С ■ sin [ n ( e p ² + e x ) ] и суммарная жесткость будет - С = С₁ + С ₂ . Для случая двух- трех парного зацепления согласно рис.5 б) для определения жесткостей зубьев, аналогично предыдущему, получим следующие выражения: параболического типа: в области двух парного зацепления - С = С₁ + С ₂ ,где C i = C k ^{+ 4} "^АС ■ [ x ^e Р ) ] ■^{[ 1 -} x ^{( e} P ^{) ] и} C 2 = C k ^{+ 4} -^АС ■ ⁽ P ⁺ x )K^e P ) Ф^{- (} P ⁺ x W ■ P ^{) ] ;} в области трех парного зацепления- С = С₁ + С ₂ + С ₃ , где еще добавляет -ся- жесткость третьей пары зубьев - C 3 = C k + 4 -А С ■ [ (2 ■ p + x )/( £ . P ) ] . [ 1 - (2 - р + x )/( £ . P ) ] .

В случае синусоидальной зависимости будем иметь: в области двух парного зацепления С = С ₁ + С ₂ ,где C ₁ = C_k + А С ■ sin [ n ( e ■ р ) ■ x ] , а C ₂ = C_k + А С ■ sin [ n ( e ■ р ) ■ ( р + x ) ] .

В области трех парного зацепления- С = С ₁ + С ₂ + С ₃ , где еще добавляется жесткость С ₃ = C_k + А С ■ sin [ n ( e ■ Р ) ■ (2 ■ р + x ] . В случае трех- четырех парного зацепления согласно рис. 5г) соответственно будем иметь: зависимости параболического типа в области трех парного зацепления- С = С ₁ + С ₂ + С ₃ , а в области четырех парного- С = С ₁ + С ₂ + С ₃ + С ₄ , где- C 4 = C k + 4 ^А С - ^ р + x ⁾/^{( e} ■ р ) ■^{[ 1 - (3} р + x ⁾/^{( e} ^ p ^{) ]} , а при синусоидальной аппроксимации С ₄ = C_k + А С ■ sin [ ( n ( e ■ р ) ■ (3 ■ р + x ) ] . Эти все зависимости использовались при численном исследовании параметрической динамики упрощенной модели редуктора

Параметры зацепления солнечного колеса с сателлитами дифференциального редуктора исследуемого изделия следующие: число зубьев солнечного колеса - z = 36 ; модуль зацепления - m = 4,6 мм: угол зацепления в полюсе - а = 25,42⁰ ; коэффициент перекрытия - e = 1,31 ; суммарная рабочая длина зубьев - b _z = 85,8 мм, зазор в зацеплениях - 5 = 0,2 мм (эти данные

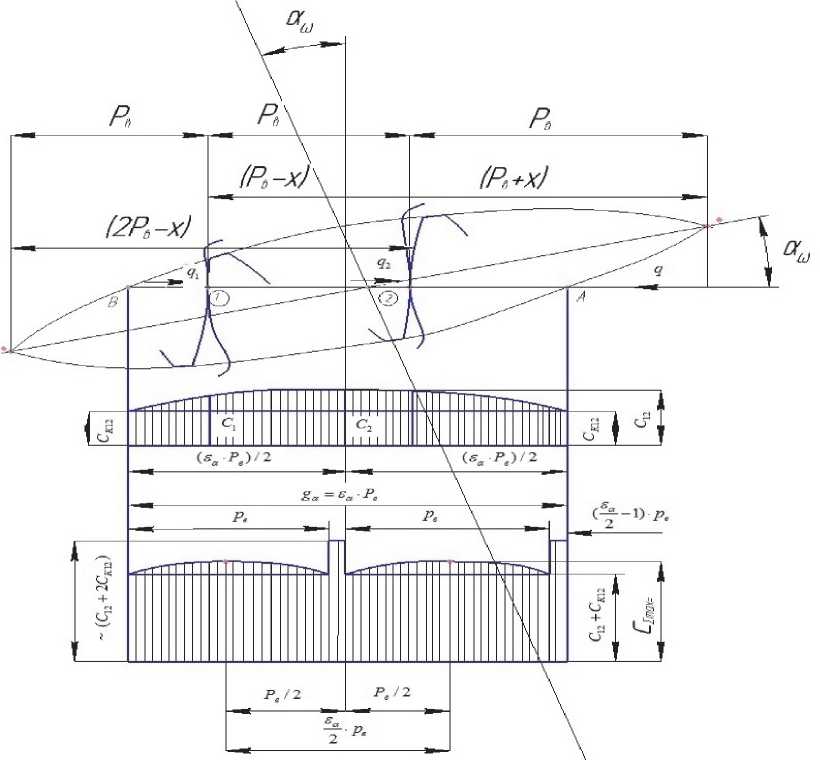
Рис. 6. Геометрические параметры и характер изменения жесткости при трех парном зацеплении

взяты из технического описания исследуемого изделия).

При расчетах динамики изделия было принято допущение, что усилия между сателлитами распределяются равномерно. Тогда при числе сателлитов редуктора - а с = 3 , значения жесткостей зубьев для нашего изделия: в середине шага зацепления пары зубьев - C O = c o - b z - a_c = 18000 - 85.8 - 3 = 4623200 H / мм ; а в начале и конце шага зацепления пары зубьев - C K = c k - b z - a_c = 12500 - 85,8 - 3 = 3217500 H / мм .

В упругую модель исследуемой системы включено так же шлицевое соединение между солнечным колесом и приводным валом. Параметры шлицевого соединения следующие : число шлиц - z_ш = 44 ; модуль зацепления шлиц - т ш = 2,5 мм; длина шлиц - Ь ш = 40 мм. Удельная окружная жесткость одной пары зубцов шлиц на основании литературных данных и нашими исследованиями принимается равной c_Ш = 16000 Н / мм ² . Тогда жесткость на кручение всего шлицевого соединения будет Си, = c„ - Ьц , - 2_И, = 16000 - 40 - 44 = 281 6000 H / мм . Ш шШШ

Радиус основной о кру жно -сти шлицевого соединения - ^Гош = ^тш ^{- Z}ш ^- И « ош ) ^/2 = ^{2,5 - 44 - cos(300)/2} = ^38,45 мм , где - а _ош = 30 0 угол исходного контура инструмента при нарезании эвольвентных шлиц. При двух- трех парном зацеплении и перекрытии незначительно больше двух третья пара зубьев входит в зацепления на очень короткое время и. геометрические параметры и характер изменения жесткости при двух- трех парном зацеплении показаны на рис. 6.

Далее мы попытаемся существующее однодвух парное зацепление исследуемого редуктора заменить двух- трех парным зацеплением при следующих условиях: сохраняем - межосевое расстояние - a w = 201 мм, модуль зацепления - m = 4,6 мм, и числа зубьев: солнечного колеса - z 1 = 36 и сателлитов - z ₂ = 48 . Это делается для того, чтобы не изменять размеры всех остальных зубчатых колес в существующем редукторе и чтобы не изменились частоты возбуждения упругой системы изделия зацеплениями зубьев редуктора. Чтобы эти условия выполнить, необходимо спроектировать новый исходный контур инструмента для изготовления зубчатых колес.

РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ДВУХ - ТРЕХ ПАРНОГО ЗАЦЕПЛЕНИЯ

Методика геометрического расчета двух- трех парного зацепления при принятых условиях следующая. Дано: aw = 201 мм, m = 4,6 мм, z 1 = 36, z2 = 48. Коэффициент радиального зазора принимаем по ГОСТ - co = 0,25 Дальнейшие расчеты производим методом последовательных приближений добиваясь оптимальных параметров зацепления: чтобы было потребное перекрытие £ > 2 и чтобы было допустимое заострение зубьев цементированных колес. Задаемся начальными значениями угла исходного контура инструмента - ао и коэффициентом высоты головки исходного контура инструмента -h^. Далее ведем расчет по гостовской методике. Делительные диаметры: шестерни - d 1 = m - z 1 , колеса - d2 = m - z2. Делительное межосевое расстояние - ащ = (d 1 + d2) / 2. Диаметры основных окружностей: шестерни - do 1 = d 1 - cos(ao) , колеса - d02 = d2 - cos(ao) . Угол зацепления в полюсе - cos(aw ) = (ao/aw ) - cos(ao) . Сум -марный коэффициент смещения инструмента -x z - 0.5 - (z1 + z 2) / tg (aw). Задаемся отношением коэффициентов смещения x 1 / x2 = Ox. Тогда коэффициенты смещения при нарезании: колеса x 2 = x z /(1 + Ox ), шестерни - x 1 = x 2 - Ox .Диаметр впадин: шестерни - df 1 = d 1 - 2 - (h^ + co - x1) - m, колеса df 2 = d2 - 2 - (hfo + co - x2) - m. Диаметры вершин: шестерни - de 1 = 2 - (aw - co - m) - df 2 , колеса - de 2 = 2 -(aw - co - m)- df 1 . Углы профилей в вершинах зубьев: шестерни - cos(ae 1) = de 1/ do 1, колеса -cos(ae2) = de2 / do2. Коэффициент перекрытия - £ = (do 1 - tg(ae 1) + do2 - tg(ae2) - aw *„))/ Pi - m - cos(ao ) > 2 . Далее итерируется коэффициент высоты головки зуба - hf = hfi + Ahf до тех пор пока коэффициент перекрытия примет нужное значение - £ > 2. После этого нужно проверить заострение зубьев, что важно для цементированных или азотированных колес. Толщины зубьев по делительным окружностям: шестерни - 51 = (pi /2 + 2 - x1 - tg(ao))- m , колеса - 5 2 =( pi/2 + 2 - x 2 - tg (ao))-m . Толщины зубьев по вершинам: шестерни: 5a 1 = da 1 - (51 /d1 + inv(ao) - inv(ae 1))> 0.4 - m, колеса - 5a2 = da2 - (s2 /d2 + inv(ao) - inv(ae2)) > 0.4 - m . Здесь инволюты - inv(ao) = tg(ao)-ao, inv(ae 1) = tg(ae 1) - ae 1 , inv(ae2) = tg(ae2) - ae2 .

Если эти условия не выполняются, то изменяется (итерируется) значение коэффициента распределения коэффициентов смещения инструмента при на резании зубьев - x1 / x2 = Ox . И снова повторяется расчет по изложенной методике. При изменении значения коэффициента - Ox надо стремиться сделать равными толщины зубьев в вершинах сопряженных колес. И так методом итерации находится приемлемый вариант параметров исходного контура инструмента для нарезания зубчатых колес с дух - трех парным зацеплением. Можно сделать инструмент с закру- гленной головкой. Радиус закругления головки исходного контура инструмента определяется по зависимости - р = [п /4 - Н^ • tg(ao )]• m I tg(ao).

Так для принятого варианта рассматриваемого изделия при коэффициенте перекрытия £ = 2,1 в ниже приведенных расчетах найдены по приведенной методике и приняты следующие параметры исходного контура инструмента: модуль зацепления солнечного колеса и сателлитов - m = 4,6 мм; угол исходного контура инструмента - a o = 12 o ; коэффициент высоты головки исходного контура инструмента - h f = 1,5972 ; радиус закругления головки исходного контура инструмента - р = 2,097 мм. Расчетные параметры двух и трех парного зацепления, заменяющие существующее в дифференциальном редукторе изделии получились следующие: межосевое расстояние - a w = 201 мм (сохранилось); число зубьев: шестерни - z_x = 36 (сохранилось) , колеса - z ₂ = 48 (сохранилось ); угол зацепления - a w = 19,92 o ; суммарный коэффициент смещения инструмента - x ₂ = 2,2912 ; коэффициенты смещения: шестерни - х 1 = 0,7637 , колеса - x ₂ = 1,5274 ; радиусы основных окружностей: шестерни - r o 1 = 80,9906 мм, колеса - r o ₂ = 107,9875 мм; радиусы начальных окружностей: шестерни - r_{w 1} = 86,1429 мм, колеса - r w ₂ = 114,8571 мм; радиусы впадин колес: шестерни - r ^ 1 = 77,8165 мм, колеса - r f ₂ = 108,9296 мм; наружные радиусы колес: шестерни - r e 1 = 90,9004 мм, колеса - r e ₂ = 122,0335 мм; коэффициенты заострения зубьев: шестерни - s e 1 / m = 0,69 , колеса - s e ₂1 m = 0,74 . На рис.7 показан эскиз исходного контура для изготовления двух - трех парного

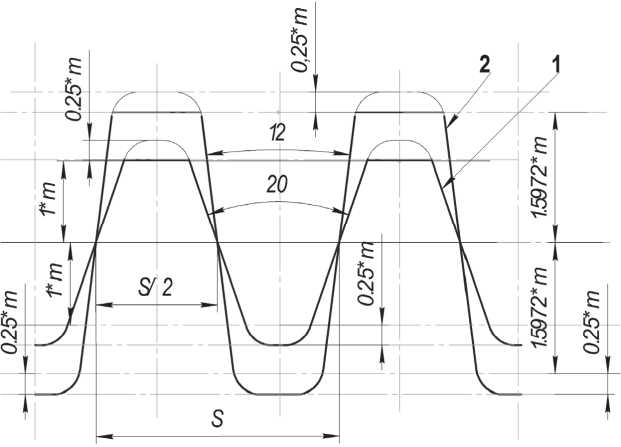
Рис. 7. Эскиз исходного контура инструмента для изготовления двух - трех парного зацепления солнечного колеса и сателлитов: 1– исходный контур зубчатых передач по ГОСТ; 2 – исходный контур для зубчатых передач с перекрытием 2,1

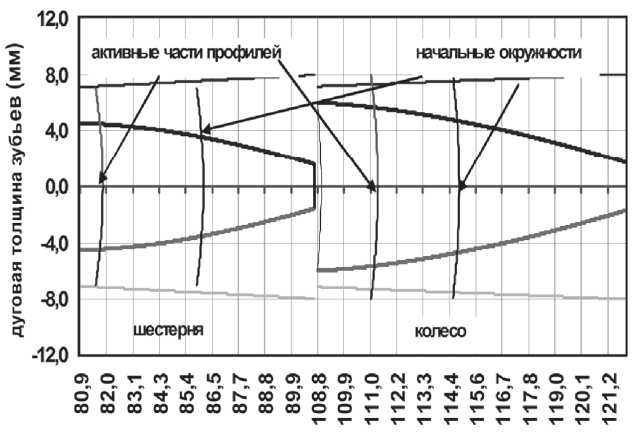
радиус (мм)

Рис. 8. Профили зубьев зубчатых колес, изготовленных спроектированным инструментом

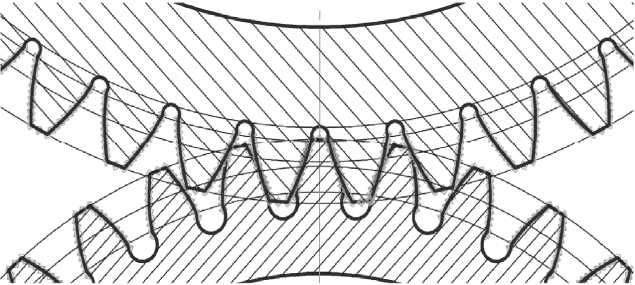
Рис. 9. Фрагмент зацепления, построенных по программе КОМПАС для модернизации существующего редуктора с одно – двух парного на двух – трех парное зацепление зацепления солнечного колеса и сателлитов существующего редуктора.

На рис. 8 показаны профили зубьев изготовленных таким инструментом (построены программой EXCEL).

На рис.9 показаны фрагмент такого зацепления, построенные по программе КОМПАС.

ЗАКЛЮЧЕНИЕ

В результате проведённых исследований была оценена жёсткость зубьев зубчатых колёс при двух и трёх парном зацеплении.

В настоящей работе предлагается замена одно- двух парного зацепления зубчатых колес на зубчатые колеса двух- трех парного зацепления. При такой замене нагрузка в районах полюса зацепления, где обычно возникает выкрашивание, расчетная статическая нагрузка уменьшается в два раза а, следовательно, можно уменьшить габариты зубчатых колес и значительно повысить их долговечность по выкрашиванию, кроме того, также значительно уменьшить перепад жесткостей в зацеплениях зубьев, что должно привести к уменьшению параметрического возбуждения и шумности упругой системы всего изделия. В зависимости от характера изменения суммарной жесткости зубьев в зацепления изменится и величина параметрического возбуждения.