Исследования физико-механических и конструктивных характеристик вибрированных, центрифугированных и виброцентрифугированных бетонов

УДК 531.36                                                  

Введение . Исследование движения прямоугольного корпуса является актуальной задачей в мобильной робототехнической сфере [1]. Это движение происходит за счет управления материальной точкой внутри корпуса. Такие мобильные роботы могут использоваться при решении задач широкого класса. Например, при создании автономных роботов для исследования космического пространства и планет. В медицинских целях для диагностики и лечения, например, при прохождении по сложным структурам вен и артерий. А также при подземных работах и проведении исследований в тяжелых условиях, например, под водой и в местах больших перепадов температур [1, 2].

Таким образом, всё новые задачи ставятся перед робототехникой, для решения которых требуются теоретические исследования, в т. ч. исследование моделей трения между корпусом и поверхностью в условиях комбинированной динамики [3, 4]. Так как движение мобильного робота происходит в разных направлениях, необходимо учитывать продольное движение и верчение. Таким образом, в структуре модели трения нужно обеспечить взаимосвязь между скоростями скольжения и верчения [5]. Важное развитие в описании данной взаимосвязи было сделано в работе [6]. Её автору удалось разрешить уравнения для главного момента и вектора сил трения, где в качестве площадки контакта рассматривался прямоугольник. Такие аналитические выражения позволяют наиболее точно описывать движение тел по шероховатым поверхностям, но они являются громоздкими и сложными, так как содержат в себе интегральные выражения. Поэтому авторы работы [7] построили дробно-линейные аппроксимации Паде, которые позволили находить решения для получаемых зависимостей.

С помощью аппроксимации Паде можно объяснять действия комбинированного сухого трения для линейных и угловых скоростей. На основе приближений Паде появилась возможность создавать новые модели трения [8, 9], которые впоследствии начали классифицировать для лучшей интерпретации [10]. Классификация происходит в зависимости от числа параметров. Так, в работе [11] авторы ввели понятия размерности и порядка модели сухого трения в зависимости от порядка используемых Паде-аппроксимаций.

Модель трения скольжения и верчения, которая предлагается в статье [12] дает возможность учитывать динамическую связь компонентов, которые определяют силовое взаимодействие прямоугольного корпуса и горизонтальной поверхности [13].

Механика

Постановка задачи. Рассматривается твердое тело массой m ₀ , которое представляет собой прямоугольный корпус с однородными гранями длиной а , шириной b и высотой 2 h . Вводится неподвижная система координат Oxyz , связанная с корпусом (рис 1). Точка O находится на горизонтальной плоскости. Система O ₁ x ₁ y ₁ z ₁ имеет начало в точке O ₁ , которая соответствует геометрическому центру корпуса. Ось O ₁ z ₁

параллельна оси Oz . Ось O ₁ x ₁ параллельна длинному ребру корпуса. Введем единичные векторы e_x , e_y осей O ₁ y ₁ и O ₁ x ₁ соответственно.

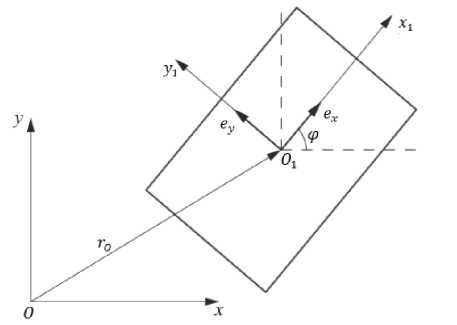
Рис. 1. Системы координат

Рассмотрим безотрывное движение корпуса по поверхности (рис. 2), которое состоит из поступательного перемещения и вращения относительно оси O ₁ z ₁ . Три координаты определяют положение корпуса. Координаты x ₀ , y ₀ и h задают начало системы координат O ₁ x ₁ y ₁ z ₁ в координатах Oxyz . Поворот корпуса относительно его исходного положения по оси 01x1 задается углом ф. В настоящей статье рассматривается случай, когда центр масс корпуса G и центр масс системы O ₁ совпадают (рис. 2) [14].

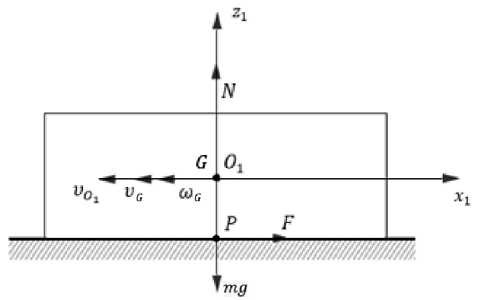
Рис. 2. Движение корпуса системы

Материалы и методы. Область контакта представляет собой прямоугольник со сторонами a и b , в котором нормальное напряжение зависит от расстояния от точки P до граней прямоугольника (рис. 3).

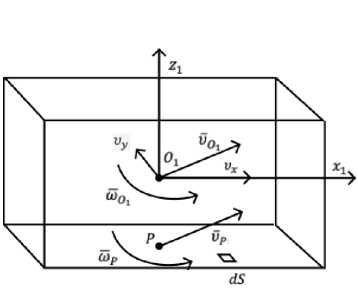
Рис. 3. Скорости точек O ₁ и P

Рассмотрим бесконечно малую площадь dS в произвольно выбранной точке M на поверхности контакта. Введем угол φ между относительной скоростью скольжения и осью O ₁ x ₁ . Проведем радиус-вектор rM,_p из точки P к точке М . Вектор скорости точки M обозначим и_м, для его нахождения используем формулу Эйлера, описывающую распределение скоростей в абсолютно твердом теле:

Um — Up + W ' ^ Mp .

Скорость скольжения в точке M раскладывается на две составляющие вдоль осей 0 1 x 1 и 0 1 у 1 :

u_M x — U x - ум;

u_My — u_y + xto.

Используя закон Кулона, найдем малое приращение силы трения, направленной против относительной скорости в точке M [15]:

dF — -foC^^dS, |им| где f — коэффициент трения; o(x, у) — функция распределения контактных напряжений, зависящая от координат x и у; dS — dxdу — малое приращение площади [15].

Перепишем дифференциал силы трения и момент этой силы в проекциях на рассматриваемые оси: dF_x — -fo⁽x,y⁾ U ^^ dxdy;

dF_y — -fo(x,y) U ^^ dxdy;

[ i J    M dMz — x   у 0 — xdFy - уdFx.

dF_x  dF_y 0

В качестве частного случая рассмотрим равномерное распределение напряжения при отсутствии внутренних масс в корпусе, тогда эти напряжения будут равны: о = ^ 0 2 , но далее запись продолжим в общем виде: o(x,y).

Проинтегрировав выражения для сил трения, получим:

F x —	■                   x                xd.
F y —	/Г . j". ' o(x.V) ;+X dxdv.

Модуль относительного скольжения |u_m| вычисляется по формуле:

|им|

^Ju Mx ^{+ U} My

Ju X + u y + M ² (x ² + у ² ) + 2to(u_yx - и_ху).

Представим взаиморасположение векторов переменной скорости скольжения U и составляющих силы трения: F|| — составляющая, направленная в противоположном направлении относительно скорости скольжения и; F_l — составляющая, перпендикулярная мгновенной скорости проскальзывания. Одновременно представим координацию этой системы относительно осей 0 1 x 1 и 0 1 у 1 (рис. 4).

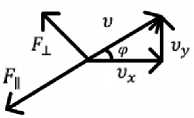
Рис. 4. Составляющие силы трения и скорости

Осуществим переход от проекций скорости скольжения:

г их — ucos^, {uy — usin^, к модулю скорости и углу скольжения:

( F — F_xcos^ + F_ysin^, {F_l — F_x(-sinv) + F_y sin^.

Проинтегрируем момент силы трения на площадке контакта:

Mz —

-

r ^a/2 c^b/2 __{(y v)} ^^Х^ПС-1£ОФ±С1Х^1^^ л_гл_г

-tt^J-lV ²    ,    /U'+^TX ^ +yT+^^UXsTn^—ycos^)

Подставим в систему (5) выражения (1)-(3), а также перепишем выражение для момента силы. В результате получим трехмерную модель трения скольжения и верчения:

Механика

„ _ - г а/2 гЬ/2   ,    х v(cos ² ^+sin ² ^)-^(ycos^+xsin^)  ,  ,

¹    ^^- п ^/2^^- ь ^/2   , у ^и2+^ycos^)   у ;

F

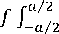
b/2                   w(ysinQ+xcosQ)

I . o(x, y) • .,,,,,               ■ dxdy;

^{-b/ 2}          Vu ² +^ ² (:r ² +y ² )+2^u(:rsin^-ycos^)

M z

^^^^e

p cz/2  rb/2   (    л      u(xsin^-ycos^)+w(x ² +y ²)     ,  ,

^- a ^/2^^-b/2     , У   Уи ^ +ш ^ ^у ^ +У^^+^шиСх^Гпф—ycos^)     У

Для того, чтобы не решать громоздкие интегралы, используют замену соответствующими разложениями Паде [16, 17]. Таким образом, исходя из теории Паде [18], эти выражения могут формулироваться как отношение двух функций нескольких переменных во всей области определения при условии, что функции должны иметь одинаковый порядок [7]. Для определения этих функций необходимо определить поведение интегральных выражений (6)-(8) при следующих условиях:

ЭР^     _ / га/2 rb/2   ,    , 7x2+y2(x2+y2) + (ycosV+xsin^)(zsin^-ycos^) , , _/^

3u |u=Q      ш ^-а/2 '-b/2°^ ,У'                      (x2+y2)2                         У

ЭМ2

^Эu |u=0

—

£ ,а/2 _f^b/2          , (2y £ rsinv-2y 3 cosv)        -_Lr ■

„ J - _a /2 J -b/2 °^(xy)        (x ² +y ² ) ^{2     dxdy}= ы ^ З ;

Mz^ = —f C C>(x,y)   '. dxdy = —fl₆;

• —             г гd/2 rb/2   ,    x ysin^+xcosQ J J

• ^F l|„_ = ^—f L_a /2 ^ -b/2 ° ^(x -y^ • _V x 2 +y 2 ^dxdy = ^f/ 9 ^;

of   _(F_  =3F   _F    _^   _(F_- dU|„=o dw^o dto|„=o    "|ш^”   (и |Ы=о   (W|u=o

• = F    = 2£±   =ЭМ   =эм   =м=

1|u^”   Эы |ы=о    Эu |ы=0 Эы |u=o     Z|u^”

^dF ± ^dM z

Значения выражений и —— не участвуют в нахождении последующих аппроксимаций Паде, поэтому их написание опущено в силу громоздкости. Тождественное равенство нулю реализуется при условии, когда напряжение о симметрично относительно центра прямоугольного пятна контакта, т. е. точки Р.

Точная трехмерная интегральная модель [13] (6)-(8) дает логичное описание явлений сухого трения, однако для решения задач динамики такая модель является сложно-приемлемой в силу необходимости вычисления внушительных интегралов [10]. Во избежание этой процедуры используется [6] замена точной интегральной системы на соответствующие выражения с помощью аппроксимаций Паде во всей области изменения переменных. Дробно-линейные разложения Паде дают трехмерную модель трения скольжения и верчения первого порядка [19]:

V + b 1 £.

^F "^{F o} u+d_{1 U}; „ ,     „ , w+b₇u

Mz = Mo--—;

^{Z      o} W + ^ 2 u

F   F_o ^+°^ .

^{x    o} w+d₃u

Для определения коэффициентов Паде необходимо изучить свойства этой модели в граничных точках по аналогии с интегральными выражениями. Для этого продифференцируем параметры F||, F±, MZ и тем самым удовлетворим соответствующим интегральным выражениям:

Х = -П1—— ^{u +} 7 1 ^M Mz = —f/₆ to

F i =

V

Система уравнений движения имеет вид:

.

—f^9---j— ю + 3-v j9

dtoOl

^71 = M z ; dt

⁽m o + m i ) ^ = F_z + ⁽m o + m₁⁾U y to o₁ ;

du y

⁽m o + mJ — = F y — ⁽m o + m i ⁾v_zto o₁ .

Выразим производные по времени от скорости скольжения и угловой скорости с помощью формул (3)– (5):

du

dt  27^1+^

/   duz      duy\

^{(2U r} dt ⁺ 2^{U y} dt ) ^;

dv dt

1      u sin^    u cosv m0 + m1( u2  ^+ u2  ^J.

Перепишем эти уравнения с помощью формул (3)-(5) при ш0| = ю/а и добавим первое уравнение из системы (12):

dm

⁽m o +mj^ = F,,;

(m0 + т^ф = F±.

Результаты исследования . Далее вычислим интегральные выражения параметров 1₀, 1 1 , /₃, 7₆, 1 9 с помощью программного комплекса Wolfram Mathematica при следующих значениях:

/ = 1; а = 0,5 м; b = 0,2 м; mo = 1 кг,    о = mo9/ab = 87кг/с2м и подставим в систему уравнений (13). На основе численных выражений построим графики интегральных и нормированных функций, зависимых от параметра к = u/m . На рис. 5 приведены графики функций интегральных моделей трения (11)–(13), а также моделей на основе аппроксимаций Паде (14)–(16).

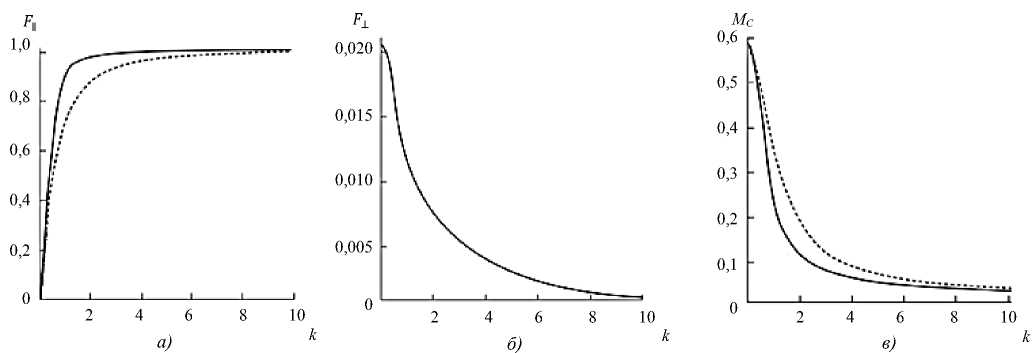
Рис. 5. Графики интегральных (сплошные линии) и нормированных (пунктирные линии) функций касательной ( а ), нормальной ( б ) составляющих силы трения и момента трения ( в )

Исходя из графиков функций (рис. 5), можно говорить о хорошем соответствии рассмотренных моделей. Далее получим графики зависимостей характерных параметров от времени (рис. 6).

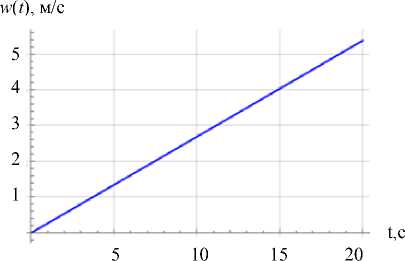
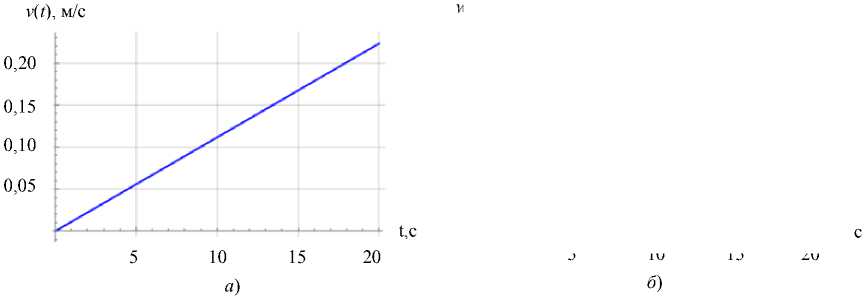
Рис. 6. Зависимости скорости скольжения v ( а ) и угловой скорости w ( б ) от времени t

Обсуждение и заключения. Выполнено описание движения мобильного робота, начиная с контакта его корпуса и опорной плоскости, в условиях комбинированной динамики, когда присутствует скольжение и верчение. Получены аналитические интегральные выражения для касательной и нормальной составляющих силы трения [19] и момента трения применительно к прямоугольной площадке контакта. Для полученных выражений определены соответствующие аппроксимации Паде. Проведено сравнение интегральной и

Механика

нормированной моделей посредством построения графиков зависимостей сил трения и момента трения от угловой скорости и скорости проскальзывания. Результаты сравнения показали хорошее соответствие интегральной модели и модели на основе разложений Паде. Графики соответствуют логичному поведению при движении прямоугольного корпуса, т. к. скорость скольжения и угловая скорость увеличиваются соответственно заданным параметрам. Следовательно, комбинированная модель трения, реализованная с помощью аппроксимаций Паде, может быть применена для решения задач, связанных с мобильными подвижными роботами с прямоугольным основанием.