Исследования несовершенных коллоидных многогранных структур

Многогранники Кокстера формируют форму коллоидных кластеров. Приведенные в наших работах [1-5] каустики (энергетическое отображение ионных потоков) вполне структурно очерчены. Модели, в которых рассматриваются соударения кластеров (составляющих их частиц), описываются и соответствуют формированию ударных волн в форме гелевых каустик в местах их взаимодействия. Эти энергетические рефлексы суть явления гелевой волновой интерференции или дифракции в коллоидных системах [2]. При этом создаются многообразия движущихся волновых фронтов, которые определяются пульсационным движением нанокластеров в потенциальном поле коллоида (рэтчет-потенциалы), определяющих скорости их перемещения [6]. Ранее была рассмотрена задача, связанная с поведением малых частиц оксигидратного геля – нанокластеров [7]. В геле постоянно происходят стохастические неравновесные диссоциативно-диспропорциональные [8] толчковые (относительно низкотемпературные) явления с выбросом третьих кластерных (в основном нанокластерных) частиц в дисперсионную фазу, которые отвечают за диссипацию энергии в неравновесной оксигидратной системе. Отщепление отдельных частиц геля, которые обычно несут заряд, либо их присоединение к крупным фрагментам макромолекул, от которых ранее они отщепились, инициируют токовые периодические пульсации [9]. Отщепившиеся третьи заряженные кластеры геля перемещаются в пространстве под воздействием стохастических электрических полей в достаточно узком пространстве коллоидного геля. Их можно легко регистрировать, если поместить в это пространство хорошо электропроводящие платиновые или графитовые электроды, связанные с приборами усиления [10].

Перестройки этих сформированных фронтов движущихся кластеров есть перестройки каустик [11], исследуемых в “пространстве-времени”. Объединение фронтов в различные моменты времени образует некую гиперповерхность в этом пространстве. Гиперповерхность, образованная типичными движущимися фронтами кластеров, сама является фронтом типичного лежандрова отображения подмногообразия, размерность которого на 1 больше размерности изучаемого движущегося фронта [6]. Поэтому гиперповерхность в пространстве-времени, образованная фронтами в различные моменты времени, будет называться большим фронтом. Особенности больших фронтов, образованных в пространстве-времени перестройками в типичных семействах движущихся фронтов, известны. Если исходное пространство трехмерно, то особенности типичных больших фронтов диффеоморфны дискриминантному многообразию группы A4 или D4 [5, 10, 11]. Возможны также трансверсальные их самопересечения [7, 12-14].

В теории динамических систем известно [14-16], что в двухмерной гидродинамике (в т.ч. коллоидных растворов) могут существовать перемещения кластеров, которые имеют симметрию или квазисимметрию [17]. Это связано с тем, что гамильтоновские системы в общем случае являются “носителями хаоса”, при некоторых минимальных ограничениях фазовое пространство динамической оксигидратной гамильтоновской системы имеет области, внутри которых происходит движение с перемешиванием. Гамильтоновская система явно зависит от времени и является периодической. Есть установление сосуществования в фазовом пространстве областей устойчивой динамики и областей хаоса. Зародышем хаоса [17] являются стохастические слои, образующиеся в окрестности разрушенных сепаратрис колебательного движения при их толчковом возмущении. Области разрушения сепаратрис соответствуют областям разрыва донорно-акцепторных связей (водородных связей) в ок-сигидратных кластерных системах. При стохастическом возмущении, сопровождающем разрушение сепаратрис, наблюдается формирование стохастического резонанса. При этом отмечается пульсационное формирование и перемещение свободных кластерных частиц ГУИ или ШТЕРНА в дисперсионной гелевой среде.

По Арнольду, предсказания теорией особенностей геометрии каустик, волновых фронтов и их внутренних перестроек связаны с кристаллографическими группами Кокстера (Дынкина), с классификацией правильных многогранников, например в трехмерном евклидовом пространстве [12]. В многограннике Кокстера двугранные углы являются целыми числами π. Вопрос о многогранниках Кокстера может быть поставлен в любом из трех типов пространств постоянной кривизны: сферическом Sn, евклидовом En и Лобачевского Ln. Семейство полупространств однозначно определяется по многограннику. Полупространства, входящие в семейство, назы- ваются определяющими многогранниками. Границы полупространств, определяющие многогранник, называются гиперповерхностями граней, а их пересечения с многогранником – его гранями старшей размерности (или “гранями коразмерности 1”). Гиперплоскости граней являются (n-1) – мерными пространствами, а грани – многогранниками в них. Грани размерности 1 называются ребрами, а размерности 0 – вершинами. Любое евклидово полупространство в En задается в виде линейного неравенства a1x1 + a2x2 + … anxn ≥ c, где коэффициенты a1, a2, … an являются координатами вектора нормали к гиперплоскости – границе полупространства.

Двугранный угол образован в пересечении выбранных полупространств. Величину угла можно определить как величину плоского угла, получаемого в пересечении этих полупространств с двумерной плоскостью, перпендикулярной их границам. Таким образом, определенный угол между полупространствами дополняет до π угол между нормалями к ним. Угол между гранями многогранника называется углом между соответствующими этим граням полупространствами. Если две грани старшей размерности пересекаются по граням коразмерности 2, то они называются смежными, а угол между ними называется двугранным углом многогранника.

Экспериментальная часть

Для анализа токовых процессов, протекающих в неравновесной гелевой фазе, временной интервал между замерами должен быть небольшим. С этой целью использовали модульные измерительные системы L-CARD c модулем E-270, частотой опроса 5 замеров в секунду, а также измерительную систему ZETLab, включающую усилитель ZET410 с измерительным блоком ZET 210. Данные модули являются универсальными программноаппаратными устройствами для использования со стандартной шиной USB, предназначенными для построения многоканальных измерительных систем ввода, вывода и обработки цифровой информации. Выбираем графитовую плоскость S, заданную уравнением x_i = const, и отмечаем точки пересечения траектории орбиты Г (решения уравнения (1) с плоскостью S соответствуют заданному направлению эволюции ( x & <  0)). Траектория Г пересекает S в точках P 0 , P 1 , P 2 , …. Таким образом, можно получить множество точек, образующих сечение Пуанкаре, то есть граф в двух измерениях. В оксигидратных гелях мы имеем дело именно с ионными потоковыми движениями. Как нам представляется, для получения объемных фазовых изображений заряженных кластеров оксигидратных частиц необходимо получить точки (сечения) Пуанкаре всего объемнопространственного кластерного габитуса. Для этого секущая поверхность или поверхности должны перемещаться в пространстве по определенному известному закону, нормально пересекая орбиты движущихся кластеров. С этой целью создана установка с вращающимся графитовым цилиндрическим электродом (рис. 1) и приставка к прибору (рис. 2) в форме стакана с вклеенным электродом круглого сечения на его дне. Относительно этого неподвижного электрода (рис. 3) замеряли разность потенциалов вращающего графитового электрода, который снабжен электросъемниками прижимного действия. На рис. 1 эти электросъемники прижимного действия хорошо различимы [3].

Результаты и их обсуждение

На экспериментальных каустиках оксигидрата железа (II, III) и оксигидрата иттрия можно выделить кластерные перестроечные семейства, близкие или совпадающие с типичными перестройками каустик в трехмерном пространстве лагранжевых многообразий [10]: D4+; A4, (A3); D5. Следовательно, кластеры геля, или их энергетические лагранжианы – каустики, свидетельствуют об определенной упорядоченности нанокластеров, их кристалличности, хотя и имеют элементы хаоса.

Съемки фазовых портретов оксигидрата железа (III) на установке с вращающимся графитовым электродом и измерительной системой ZETLab позволили обнаружить доменную природу строения этой коллоидной системы. Такая доменная разообщенность хорошо прослеживается на рис. 1. Экспериментальные домены на рис. 4 ограничены вертикальными линиями, которые характеризуют падение потенциала на границе домена до низших значений. Фазовые портреты, построенные выборочно для двух случайных доменов (a, b), оказываются близкими по геометрической форме. Ширина доменных областей геля различается.

При более точном описании гелевых волновых проявлений появляется новый важный параметр – длина волны. Лучевое описание пригодно лишь в случае, когда эта длина волны мала по сравнению с характерным геометрическим размером системы кластеров. Интенсивность каустиковых рефлексов пропорциональна симплексу l ^-α, где l _– длина волны, а показатель α _– рациональное число, зависящее от характера особенностей. Поэтому ярче всего отображаются особенности типа пирамиды и кошелька. Отображения являются наиболее характерными для каустиков оксигидрата иттрия, апплицированного бихромат-ионами, и менее выражены у оксигидрата железа [6]. Иногда эти рефлексные отображения могут даже разрушать колебательную среду геля.

Насколько распространены и многозначны найденные метеморфозы каустик оксигидрата железа и иттрия? Геометрический характер гелевых каустик определяется химической природой матрицеобразующего элемента, а также особенностями синтеза гелей. Например, апплицированные бихромат-ионами [1] образцы оксигидрата иттрия дают наиболее яркие рефлексы типа ласточкина хвоста, а также пирамиды и кошелька, чем гели оксигидрата железа. Следует более подробно разобраться с физическим смыслом параметра α.

В математике [10-12] известно, что простые особенности каустик и волновых фронтов образуют две бесконечные серии A k и D k и три исключительные особенности E k (группы симметрий A k и D k – это группы правильных многогранников в трехмерном пространстве, а исключительные особенности E k – группы симметрий тетраэдра, октаэдра и икосаэдра). Это следует из диаграммы Кокстера-Дынкина [6]. Таким образом можно полагать, что правильные многогранники Кокстера формируют группы симметрий A k и D k .

Рис. 1. Фотографии экспериментальных коллоидно-химических ячеек для снятия спайковых выплесков тока самоорганизации оксигидратных гелей с вращающимся графитовым электродом

Рис. 2. Графитовая вставка в коаксиальном металлическом цилиндре

Рис. 3. Фотография нижнего пластикового стакана с встроенным неподвижным графитовым электродом

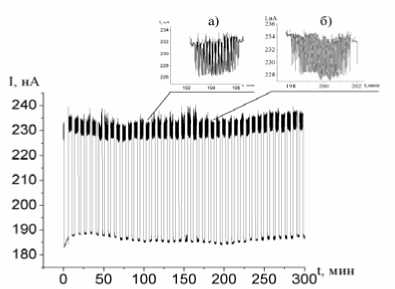
Рис. 4. Доменно-кластерная природа гелей оксигидрата железа: а) волновые домены гелей оксигидрата железа; b) фазовые портреты двух доменов, указанных стрелками

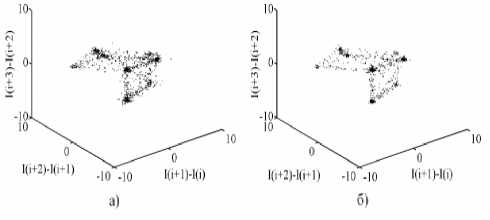
a)                                                b)

Построение многогранников Кокстера коллоидных оксигидратов по экспериментальным данным

Рассмотрим следующий алгоритм действий при построении многогранников Кокстера. Пусть имеются некоторые экспериментальные данные – величины тока, полученные через равные промежутки времени, которые можно задать формулой t i = τ∙i, где τ – промежуток времени. Обозначим вели чин у нанотока, полученную в момент времени t i , как I i . Пусть всего проведено N замеров, то есть t_i = τ ⋅ i , i ∈ 1, N .

Построим фазовую диаграмму. Обычно фазовые диаграммы строятся для производных функции, уместно построить множество точек (I i ; I i ´; I i ´), где штрихи сверху означают дифференцирование по времени. Однако численное дифференцирование является некорректной задачей, и для поиска производных необходимо строить сглаживающий функционал. Тогда мы получим сглаживание построенного решения. Нас же могут интересовать и небольшие колебания, которые неизбежно будут убраны сглаживающим функционалом. Или, наоборот, к которым сглаживающий функционал добавит систематическую ошибку. Поэтому мы воспользуемся фазовой диаграммой с разностями: ( I_i; I_i+1 – I_i; I_i+2 – 2I_i+1 + I_i ). Эти разности строятся в строчках 4-12:

n1=1;

n2=length(a)-10;

lgth=n2-n1;

for i=n1:n2

a1(i-n1+1)=a(i);

a2(i-n1+1)=a(i+1)-a(i);

a3(i-n1+1)=a(i+2)-2*a(i+1)+a(i);

end

Отметим, что строки 4-7 – вспомогательные, они выясняют, какова длина массива данных (если быть точным, то переменная n1 соответствует началу массива, а так как нумерация идет с 1, то она просто равна 1. Переменная n2 соответствует всей длине массива, то есть N. Из нее вычитается 10, чтобы избежать выхода за границы массива – с запасом).

Соответственно массивы a1 – просто токовые значения, т.е. a1 соответствует I i , a2 – разность I i+1 – I i , аналог первой производной, a3 – аналог второй производной: I i+2 – 2 I i+1 + I i .

Рис. 5. Каустика гидроксида (фазовая диаграмма) железа ( выдержка геля 66 суток) [6]

Фазовая диаграмма ( I i ; I i+1 – I i ; I i+2 – 2I i+1 + I i ) представлена на рис. 5, для построения фигуры в программе используются строки 89-90:

figure(5)

plot3(a1,a2,a3,'.k','MarkerFaceColor','k','MarkerSize',12)

Следующее построение состоит в том, что мы берем всю область фазового пространства, занятую экспериментальными точками. Находим границы по каждой из осей, то есть наибольшее и наименьшее значения по каждой оси (в программе для этого предназначены строки 14-21):

[xmax,mxmax]=max(a1);

[xmin,mxmin]=min(a1);

[ymax,mymax]=max(a2);

[ymin,mymin]=min(a2);

[zmax,mzmax]=max(a3);

[zmin,mzmin]=min(a3);

Затем строится сетка: по каждой оси берется по 11 точек, причем первая совпадает с наименьшей координатой (xmin, ymin, zmin), а 11-я – совпадает с наибольшей координатой: xmax, ymax, zmax. В результате получается 10 отрезков между 11-ю точками по каждой оси. Так как область трехмерна, то областей получится 1000. Размер области вдоль каждой из осей определяется строчками 23-25:

hx=(xmax-xmin)/10;

hy=(ymax-ymin)/10;

hz=(zmax-zmin)/10;

Подсчитаем, сколько экспериментальных точек попало в каждую область. Количество точек будем хранить в массиве amount amount=zeros(11,11,11);

а подсчет производится в строках 27-32:

for i=1:lgth nx=int16(round((a1(i)-xmin)/hx))+1;

ny=int16(round((a2(i)-ymin)/hy))+1;

nz=int16(round((a3(i)-zmin)/hz))+1;

amount(nx,ny,nz)=amount(nx,ny,nz)+1;

end

Теперь задача состоит в том, чтобы найти области фазового пространства, где наибольшее количество экспериментальных точек, и отбросить те области, где точек – наименьшее число. Для этого воспользуемся следующей процедурой: пересчитаем число областей с разным количеством экспериментальных точек. Скажем, пусть K 0 – число областей фазового пространства, где точек нуль, K 1 – число областей пространства, где точек ровно 1, и т.д. Для нахождения чисел K i предназначены строки 35-44:

for j=1:100

spx(j)=0;

for ix=1:11

for iy=1:11

for iz=1:11

if (amount(ix,iy,iz)==j) spx(j)=spx(j)+j; end end end end end

Затем будем последовательно вычитать из общей суммы областей пространства, занятых хотя бы одной точкой, эту величину. Получим некоторое

M _ ^ N к (строки 46-50) и построим соответствующую диаграм-

му (рис. 6):

allpts=sum(spx);

rss(1)=allpts;

for j=2:100

rss(j)=rss(j-1)-spx(j);

end figure(8)

plot(rss,'-k','LineWidth',3)

По виду диаграммы можно сказать, какие области отбрасывать, а какие – нет: если на полученном рисунке есть перегиб или выраженный экстремум при i =J, то оставим все области с числом точек, большем, чем J. Для этого будем использовать «переменную отсечения» Numm, которая соответствует числу J (строка 2):

Numm=10;

Программа сначала должна найти число J, и только потом можно будет выполнять дальнейшие действия, связанные с отсеиванием тех или иных областей экспериментально полученных точек. Вычисления, связанные с построением областей, лежащих выше области отсечения, располагаются в программе в строках 113-161:

figure(6)

csx=0;

smax=amount(1,1,1);

for ix=1:11

for iy=1:11

for iz=1:11

if (smax < amount (ix,iy,iz) )

smax=amount(ix,iy,iz);

nnx=ix;

nny=iy;

nnz=iz;

ppx(1)= xmin+(ix+0.5)*hx;

ppy(1)=ymin+(iy+0.5)*hy;

ppz(1)=zmin+(iz+0.5)*hz;

end csx=csx+1;

ss(csx)=amount(ix,iy,iz);

end end end spp(1,1)=ppx(1);

spp(1,2)=ppy(1);

spp(1,3)=ppz(1);

amount(nnx,nny,nnz)=amount(nnx,nny,nnz)-smax;

ikk=1;

for ix=1:11

for iy=1:11

for iz=1:11

if ( Numm < amount (ix,iy,iz) )

ikk=ikk+1;

ppx(2)= xmin+(ix+0.5)*hx;

ppy(2)=ymin+(iy+0.5)*hy;

ppz(2)=zmin+(iz+0.5)*hz;

hold on plot3(ppx,ppy,ppz,'-pk','MarkerSize',14,'MarkerFaceColor','y') hold off spp(ikk,1)=ppx(2);

spp(ikk,2)=ppy(2);

spp(ikk,3)=ppz(2);

end end end end figure(7)

K=convhulln(spp);

trisurf(K,spp(:,1),spp(:,2),spp(:,3))

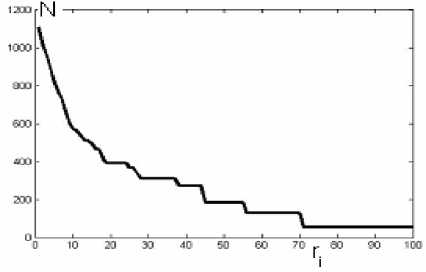
Рис. 6. График зависимости числа попаданий экспериментальных данных в ячейках определенной населенности N от населенности ячеек r. Населенность как число попаданий экспериментальной точки в одну и ту же ячейку

Построение происходит следующим образом: находим точку с наибольшим числом экспериментальных данных. Эту точку будем считать своеобразным центром нашего многогранника (ее координаты spp (:,1)). Затем находим все остальные области, удовлетворяющие условию отсечения, и помещаем их координаты в массив spp. Затем используем встроенные функции: построить выпуклый многогранник по заданному в массиве spp множеству точек (собственно координат областей с большим количеством экспериментальных точек) – функция convhulln, и построить е графически – встроенная функция trisurf. Таким образом, появится искомый многогранник. Строки с 56 по 87 предназначены для изображения разных областей, имеющих соответственно более 5, 10 и 15 экспериментальных точек (соответственно голубой, зеленый и красный цвета). В строках 163203 вычисляется матрица Грама. Для ее вычисления используется следующая схема: из стандартной функции convhulln получены отдельные грани, которые будут изображены на фигуре 7.

K=convhulln(spp);

Эти грани помещены в массив переменных K. Каждая грань представлена тремя точками, координаты которых и представляют строку массива K. На каждой грани выбираем одну точку, по двум другим строим два вектора:

v1=[spp(K(j,1),1) spp(K(j,1),2) spp(K(j,1),3)] ;

v2=[spp(K(j,2),1) spp(K(j,2),2) spp(K(j,2),3)] ;

v3=[spp(K(j,3),1) spp(K(j,3),2) spp(K(j,3),3)] ;

w1=v1-v2;

w2=v3-v2;

Их векторное произведение даст нормаль к треугольной области: w=cross(w1,w2);

Дальше осталось только пронормировать вектор на единицу и отбросить одинаковые векторы (так как процедура триангуляции часто дает одинаковые треугольники, разбивая, скажем, единую четырехугольную грань на два треугольника).

Матрица Грама строится стандартно: полученные ортонормальные векторы попарно скалярно перемножаются, так что элементы матрицы a ij = (n i ; n j )

NNN=counter;

for i=1:NNN for j=1:NNN

AMatrix(i,j)=dot(sxx(i,:),sxx(j,:));

end end

Полученная матрица AMatrix и является искомой матрицей Грама. С помощью стандартной процедуры поиска собственных значений eig(AMatrix) находим собственные значения (строка 207).

ПРИМЕРЫ РАСЧЕТА КЛАСТЕРНЫХ СТРУКТУР ОКСИГИДРАТНЫХ ГЕЛЕЙ

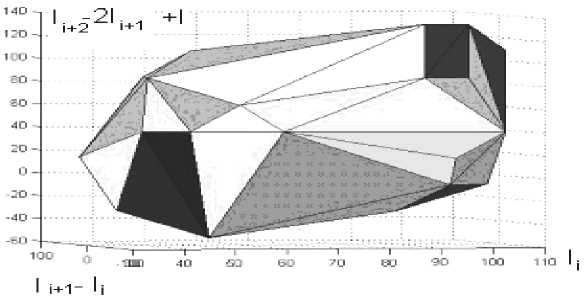
Рис. 7. Многогранник оксигидрата железа, построенный по вышеприведенной программе. По осям отложены: Ii+2 – 2Ii+1 + Ii (ось аппликат), ось абсцисс – Ii+1 – Ii и по оси ординат Ii

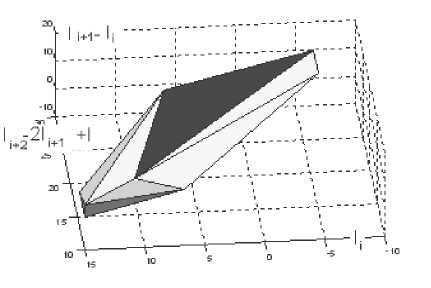
Рис. 8. Многогранник оксигидрата железа, построенный по вышеприведенной программе. По осям отложены: Ii+2 – 2Ii+1 + Ii (ось абсцисс), ось аппликат – Ii+1 – Ii и по оси ординат Ii

Матрица ГРАМА, рассчитанная для этого многогранника
through 11 1.0000	0.6971	0.7051 -0.2662	0.8571 -0.3559	0.6682 -0.4332 -0.6711	-0.3047 -0.5103
0.6971	1.0000	0.9993 -0.7422	0.3329 -0.8093	0.8870 -0.8953 -0.9348	-0.4914 -0.8605
0.7051	0.9993	1.0000 -0.7166	0.3563 -0.7866	0.8705 -0.8784 -0.9474	-0.5222 -0.8403
-0.2662	-0.7422	-0.7166 1.0000	0.2637 0.9941	-0.8948 0.9618 0.4820	-0.1135 0.9646
0.8571	0.3329	0.3563 0.2637	1.0000 0.1674	0.1918 0.0624 -0.4623	-0.4304     0
-0.3559	-0.8093	-0.7866 0.9941	0.1674 1.0000	-0.9307 0.9843 0.5679	-0.0308 0.9848
0.6682	0.8870	0.8705 -0.8948	0.1918 -0.9307	1.0000 -0.9386 -0.6694	-0.0353 -0.9800
-0.4332	-0.8953	-0.8784 0.9618	0.0624 0.9843	-0.9386 1.0000 0.7032	0.1434 0.9801
-0.6711	-0.9348	-0.9474 0.4820	-0.4623 0.5679	-0.6694 0.7032 1.0000	0.7658 0.6260
-0.3047	-0.4914	-0.5222 -0.1135	-0.4304 -0.0308	-0.0353 0.1434 0.7658	1.0000     0
-0.5103	-0.8605	-0.8403 0.9646	0 0.9848 -0.9800 0.9801 0.6260		0 1.0000
-0.9220	-0.9152	-0.9220 0.4981	-0.6767 0.5877	-0.8055 0.6874 0.8926	0.4934 0.7014
0.8559	0.7966	0.7851 -0.6932	0.4740 -0.7453	0.9346 -0.7572 -0.6019	0.0092 -0.8482
0.6832	0.8661	0.8489 -0.8825	0.2096 -0.9176	0.9985 -0.9200 -0.6400	0.0041 -0.9722
0.6056	0.4733	0.4486 -0.6695	0.2076 -0.6760	0.8084 -0.6046 -0.1722	0.4767 -0.7508
0.3148	0.2213	0.1891 -0.6281	-0.0727 -0.5987	0.6452 -0.4776 0.1232	0.7282 -0.6313
0.2821	0.4874	0.5179 0.1068	0.4049 0.0260	0.0298 -0.1472 -0.7614	-0.9996     0
-0.3367	0.2615	0.2760 -0.0829	-0.3142 -0.0960	-0.1100 -0.1987 -0.4509	-0.7217     0
-0.8455	-0.2196	-0.2361 -0.2544	-0.9647 -0.1735	-0.1988 -0.1099 0.2807	0.1776     0
Columns 12 through 19 -0.9220 0.8559 0.6832 0.6056			0.3148 0.2821	-0.3367 -0.8455
-0.9152	0.7966	0.8661 0.4733	0.2213 0.4874	0.2615 -0.2196
-0.9220	0.7851	0.8489 0.4486	0.1891 0.5179	0.2760 -0.2361
0.4981	-0.6932	-0.8825 -0.6695	-0.6281 0.1068	-0.0829 -0.2544
-0.6767	0.4740	0.2096 0.2076	-0.0727 0.4049	-0.3142 -0.9647
0.5877	-0.7453	-0.9176 -0.6760	-0.5987 0.0260	-0.0960 -0.1735
-0.8055	0.9346	0.9985 0.8084	0.6452 0.0298	-0.1100 -0.1988
0.6874	-0.7572	-0.9200 -0.6046	-0.4776 -0.1472	-0.1987 -0.1099
0.8926	-0.6019	-0.6400 -0.1722	0.1232 -0.7614	-0.4509 0.2807
0.4934	0.0092	0.0041 0.4767	0.7282 -0.9996	-0.7217 0.1776
0.7014	-0.8482	-0.9722 -0.7508	-0.6313     0	0     0
1.0000	-0.8628	-0.8003 -0.5266	-0.2207 -0.4788	0 0.5938
-0.8628	1.0000	0.9487 0.8833	0.6834 -0.0240	-0.3732 -0.5195
-0.8003	0.9487	1.0000 0.8389	0.6792 -0.0106	-0.1650 -0.2297
-0.5266	0.8833	0.8389 1.0000	0.9431 -0.4894	-0.6606 -0.3653
-0.2207	0.6834	0.6792 0.9431	1.0000 -0.7354	-0.7102 -0.1332
-0.4788	-0.0240	-0.0106 -0.4894	-0.7354 1.0000	0.7408 -0.1499

0 -0.3732 -0.1650 -0.6606 -0.7102 0.7408 1.0000 0.5531

0.5938 -0.5195 -0.2297 -0.3653 -0.1332 -0.1499 0.5531 1.0000

EigenValues (собственные значения матрицы)=

-0.0000

-0.0000

-0.0000

-0.0000

-0.0000

-0.0000

-0.0000

-0.0000

-0.0000

0.0000

0.0000

0.0000

0.0000

0.0000

0.0000

0.0000

3.4155

4.7588

10.8257

Матрица ГРАМА, рассчитанная для этого многогранника

Columns 1 through 11

1.0000 -0.3841 -0.3441 0.4075	0.9480	0.9959 0.9899 -0.9741 -0.9480		0.9132 -0.1137
-0.3841 1.0000 0.9748 -0.9425	-0.6497	-0.3918	-0.3947 0.3973 0.6497	0 -0.0580
-0.3441 0.9748 1.0000 -0.8443	-0.6249	-0.3718	-0.3861 0.4075 0.6249	0 -0.2791
0.4075 -0.9425 -0.8443 1.0000	0.6249	0.3845	0.3701 -0.3441 -0.6249	0 -0.2791
0.9480 -0.6497 -0.6249 0.6249	1.0000	0.9540	0.9538 -0.9480 -1.0000	0.7593     0
0.9959 -0.3918 -0.3718 0.3845	0.9540	1.0000	0.9987 -0.9906 -0.9540	0.9189 -0.0229
0.9899 -0.3947 -0.3861 0.3701	0.9538	0.9987	1.0000 -0.9964 -0.9538	0.9188 0.0286
-0.9741 0.3973 0.4075 -0.3441	-0.9480	-0.9906	-0.9964 1.0000 0.9480	-0.9132 -0.1137
-0.9480 0.6497 0.6249 -0.6249	-1.0000	-0.9540	-0.9538 0.9480 1.0000	-0.7593     0
0.9132     0     0     0 0.7593	0.9189	0.9188	-0.9132 -0.7593 1.0000	0
-0.1137 -0.0580 -0.2791 -0.2791	0 -0.0229 0.0286 -0.1137     0     0			1.0000
-0.9132     0     0     0 -0.7593	-0.9189	-0.9188	0.9132 0.7593 -1.0000	0
0.3913 -0.9983 -0.9603 0.9603	0.6508	0.3938	0.3937 -0.3913 -0.6508	0     0
-0.3912     0 0.3937 -0.9995 -0.9586 0.9891 0.			4298 0.4948 0.6508 -0.6508     0
-0.8249 -0.6492 -0.7171 -0.0531	-0.3269	-0.6280	-0.2297 0.7275 -0.1550	-0.0712 0.7324
-0.1953 0.3960 0.2819 -0.2969	-0.1865	0.0949	0.0451 -0.6273 -0.5305	0.9428 -0.0627
0.3041 -0.2232 -0.3536 -0.6986	-0.5991	0.4800	0.4614 -0.7863 -0.7675	0.8608 0.5517
0.4863 -0.1439 -0.3348 -0.8450	-0.7726	0.6912	0.6644 -0.9433 -0.9283	0.7248 0.5224

• - 0.6576     0 0.2420 0.8940 0.8754 -0.8650 -0.8314 0.9886 0.9821 -0.3846 -0.3776

• - 0.7263 0.9520 0.9354 0.4320 0.4834 -0.4777 -0.5356     0 0.1356 0.4248 -0.8340

0.6805 -0.7521  -0.8461  -0.8178 -0.7694  0.6710  0.6910 -0.6273 -0.6940  0.4306  0.9430 0.9268 -0.4602 -0.6640 -0.9914 -1.0000  0.9881  0.9868 -0.8654 -0.9253  0.1314  0.7337

Columns 12 through 22

• - 0.9132  0.3913 -0.3912 -0.8249 -0.1953  0.3041  0.4863 -0.6576 -0.7263  0.6805  0.9268

0 0.9603 -0.9995 -0.0531  -0.2969 -0.6986 -0.8450  0.8940  0.4320 -0.8178 -0.9914

0 -0.9983     0 -0.6492 0.3960 -0.2232 -0.1439     0 0.9520 -0.7521 -0.4602

0 -0.9603  0.3937 -0.7171  0.2819 -0.3536 -0.3348  0.2420  0.9354 -0.8461 -0.6640

• - 0.7593  0.6508 -0.9586 -0.3269 -0.1865 -0.5991  -0.7726  0.8754  0.4834 -0.7694 -1.0000

• - 0.9189  0.3938  0.9891  -0.6280  0.0949  0.4800  0.6912 -0.8650 -0.4777  0.6710  0.9881

• - 0.9188  0.3937  0.4298 -0.2297  0.0451  0.4614  0.6644 -0.8314 -0.5356  0.6910  0.9868

0.9132 -0.3913 0.4948 0.7275 -0.6273 -0.7863 -0.9433 0.9886     0 -0.6273 -0.8654 0.7593 -0.6508  0.6508 -0.1550 -0.5305 -0.7675 -0.9283  0.9821  0.1356 -0.6940 -0.9253

• - 1.0000     0 -0.6508 -0.0712 0.9428 0.8608 0.7248 -0.3846 0.4248 0.4306 0.1314

0     0     0 0.7324 -0.0627 0.5517 0.5224 -0.3776 -0.8340 0.9430 0.7337

1.0000     0     0 -0.6897 -0.0805 0.4594 0.5924 -0.6712 -0.7413 0.8134 0.9459

0  1.0000     0 -0.4932 -0.1046 -0.3788 -0.6371  0.8903  0.3277 -0.4998 -0.9378

0     0 1.0000 -0.5022  0.0696 -0.1300 -0.4284  0.7809  0.2875 -0.2771  -0.8225

• - 0.6897 -0.4932 -0.5022  1.0000  0.0504  0.0632 -0.2612  0.6844     0  0.0504 -0.5991

• - 0.0805 -0.1046 0.0696 0.0504 1.0000 0.7978 0.7553 -0.5460 0.6030 0.2728 0.1865 0.4594 -0.3788 -0.1300  0.0632  0.7978  1.0000  0.9468 -0.6844     0  0.7978  0.5991

0.5924 -0.6371 -0.4284 -0.2612  0.7553  0.9468  1.0000 -0.8826     0  0.7553  0.7726

• - 0.6712  0.8903  0.7809  0.6844 -0.5460 -0.6844 -0.8826  1.0000     0 -0.5460 -0.8754

• - 0.7413 0.3277 0.2875     0 0.6030     0     0     0 1.0000 -0.6030 -0.4834

0.8134 -0.4998 -0.2771  0.0504  0.2728  0.7978  0.7553 -0.5460 -0.6030  1.0000  0.7694 0.9459 -0.9378 -0.8225 -0.5991  0.1865  0.5991  0.7726 -0.8754 -0.4834  0.7694  1.0000

EigenValues (собственные значения)=

-4.2680

-1.5231

-1.2501

-0.7646

-0.3958

-0.0000

-0.0000

-0.0000

-0.0000

-0.0000

0.0000

0.0000

0.0000

0.0000

0.5358

0.7906

1.8974

2.4459

2.9994

4.5304

6.9286

10.0735

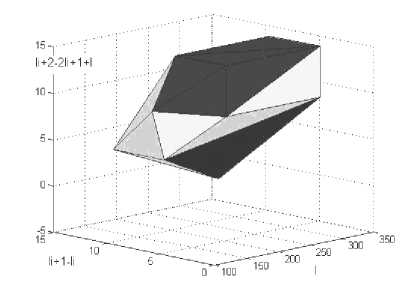
Рис. 9. Многогранник апплицированного оксигидрата иттрия ОАппИт(0.1)-3ч [17, 18]

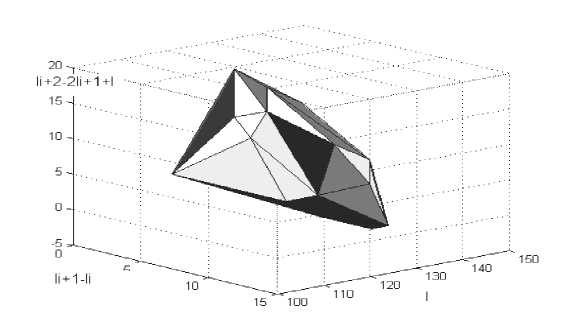
Рис. 10. Многогранник апплицированного оксигидрата иттрия ОАппИт(0.1)-1ч

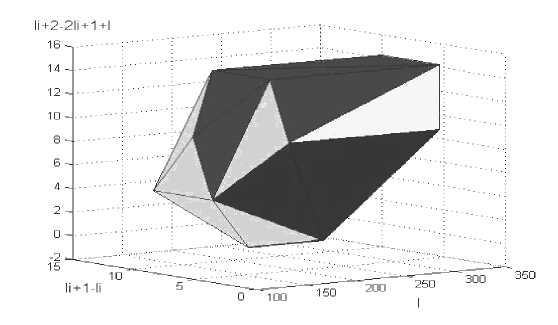
Рис. 11. Многогранник оксигидрата иттрия ОАппИт(0.1)-4ч AMatrix = оксигидрата иттрия ОАппИт(0.1)-4ч

Экспериментально установлено, что в коллоидном растворе самопроизвольно возникают небольшие токи, имеющие амплитуду до 0,1 мкА. Им соответствует очень небольшое магнитное поле, равное B = μ 0 I ≈ 10^-13 Tл. Несмотря на малость поля, на коротких расстояниях оно может создавать неслабые силы. Принимая размер кластера геля за 10^-6 м, получим поля в B=μ 0 I/α ≈ 10^-8 Tл. Поля заметны для легких подвижных частиц, движущихся на небольшом расстоянии от гелевого кластера. Если заряженная частица имеет массу молекулы воды и колеблется около положения равновесия со скоростью 600 м/сек, то сила, которая на нее действует со стороны магнитного диполя (тока), составит F = qνB = 1,67∙10^-19∙600∙10^-8 ≈ 10^-24 H. Принимая во внимание массу молекулы воды, получим, что ускорение, сообщаемое силой, будет порядка 1 м/с. Это ускорение невелико, но сравнимо с характерными скоростями колебаний молекул воды. Воздействие на диполь, имеющий магнитный момент, будет слабее, но может привести к медленной переориентации магнитного момента, что неизбежно приведет и к переориентации самой малой частицы. Из этого следует, что дипольные магнитные моменты в коллоидах необходимо принимать во внимание. Эффекты, измеренные в эксперименте, по порядку величины невелики, но они, во-первых, существуют, во-вторых, они действуют самосогласованным образом на довольно большую группу частиц, которая окружает гелевый кластер, имеющий магнитный дипольный момент. Их воздействие может приводить к неожиданным последствиям: могут возникать перегибы длинных гелевых молекул, вызванные приложением магнитных моментов.

Перейдем к конкретным вычислениям, рассчитав некоторые параметры дипольного момента. Рассмотрим трехмерную диаграмму токов, где по осям отложены ток, его «первая разность» ΔI i ≡ I i+1 – I i , разностный аналог первой производной и его «вторая разность» – величина Δ²I i ≡ I i+2 – 2I i+1 + I i , аналогичная второй производной. В диаграмме получены некоторые – достаточно формальные – плоскости, ограничивающие область, в которой находится фазовый портрет колебаний. Тем не менее эти плоскости ограничивают фазовую область. Смысл этой достаточно формальной границы: плоскость в фазовом пространстве означает связь между тремя величинами – током и его первой и второй разностями. Это означает, что существует линейная функция вида α (Δ²I) + b(ΔI) + c(I) + d = 0, где нормированный на единицу нормальный вектор к границе фазовой области n = { a ; b ; c } , a d — расстояние до центра координат. Если рассмотрим уравнение электрических колебаний, то оно будет иметь вид: LdI/dt + RI + q/C = E, где L – индуктивность контура, R – активное сопротивление, C – емкость цепи, q – заряд, прошедший через цепь, I = dq/dt – ток, он же – производная заряда по времени. Если уравнение продифференцировать, то получим соотношение: Ld²I/dt² + RI´ + I/C = dE/dt. Можем сопоставить вторую производную с коэффициентом τ, вторую разность первой производной – первую разность уравнения α (Δ²I) + b(ΔI) + c(I) + d = 0. Тогда получим, что коэффициент нормального вектора τ² α сопоставим индуктивности, τ b – активному сопротивлению, c =1/C, а коэффициент d определяет производную по времени электродвижущей силы. В результате получаем, что каждая грань многогранника соответствует некоторому элементарному току со своими параметрами – частотой колебаний и добротностью, а также внешней вынуждающей колебания силой. То есть токовая ячейка представляет собой некий элемент, состоящий, по-видимому, из нескольких контуров, взаимодействующих определенным образом.

Можно, руководствуясь аналогией, вычислить период колебаний такого диполя-токовой плоскости: T = 2 к JLCj = 2 к /_ат ²1 = _т a- . Скажем, если т = 0,2c, а = 0,1, c = 0,4, получим, что период равен 0,1 с. cc

Можно предположить, что гелевые коллоидно-химические кластеры, имеющие магнитный дипольный момент, формируют стохастические неравновесные диссоциативно-диспропорциональные [17, 18] толчковые (относительно низкотемпературные) процессы с выбросом третьих кластерных (в основном нанокластерных) частиц в дисперсной фазе. При этом некий определенный магнитный диполь, или токовый диполь, взаимодействует с другими диполями и изменяет общую геометрическую конфигурацию кластерной системы.

Выводы

• 1.    Предложен принципиально новый метод расчета кристаллографических структур оксигидратных гелей, трансформирующихся во времени. Простые особенности каустик и волновых фронтов образуют две бесконечные серии A k и D k и три исключительные особенности E k (группы симметрий A k и D k – это группы правильных многогранников в трехмерном пространстве, а исключительные особенности E k – группы симметрий тетраэдра, октаэдра и икосаэдра). Это следует из диаграмм Кокстера- Дынкина [6].

• 2.    Приведены принципы составления программы “КОКСТЕР” для реализации метода расчета оксигидрат-ных кристаллографических структур.

• 2.    Для примера рассчитаны структуры гелей, таких как оксигидрат железа (III), оксигидрат иттрия, апплици-рованный и неапплицированный.