Исследования реакции сложного узла подземных сооружений при землетрясениях как система с одной степенью свободы

Введение. Основная задача детерминированного анализа сейсмодинамики сложного узла подземных сооружений – определение характера изменения во времени перемещений заданной системы под действием сейсмической силы. Математические выражения  определяюшие сейсмодина-мические перемещения, называются уравнением сейсмического движения подземных сооружений [Мухитдинов А.Б., Абдуганиев А., Соатов А.М., Айнақулов Х.А., Мухитдинов А.А. Отбор объектов для практических работ студентов по черчению //Молодой ученый. – 2016. – №. 2. – С. 113-117., Соатов А. М., Мухитдинов А. А., Абдуллаев У. УЧЕБНО ПРОИЗВОДСТВЕННЫЕ ЗАДАЧИ В КРУЖКОВЫХ РАБОТАХ //Передовые инновационные разработки. Перспективы и опыт использования, проблемы внедрения в производство. - 2019. - С. 200-202.]. В результате решения этих сейсмических уравнений движения можно определить искомые функции изменения сейсмических перемещений во времени.

Литературный обзор и методы исследование. Вывод уравнений сейсмодинамического движения подземной системы представляет собой, по-видимому, самый важный этап всего анализа.

Получения, сейсмического уравнения движения сложного узла подземных сооружений на основе принципа Даламбера представляет собой выражения второго закона Ньютона который устанавливает, что скорость изменения импульса любой массы равна действующей на нее силе [Абдуганиев А. и др. Межпредметные связи черчения с геометрией-важный фактор активизации мышления студентов //Передовые научно-технические и социально-гуманитарные проекты в современной науке. - 2018. - С. 85-87.].

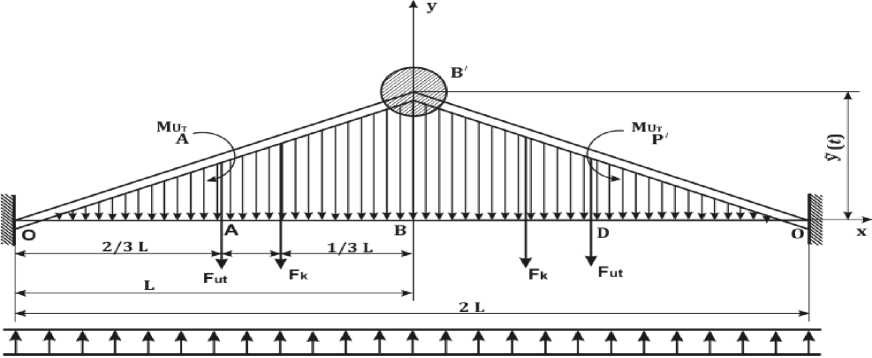
Рассмотрим поперечное колебания сложного узла подземных сооружений при землетрясениях, при этом примем что она абсолютно жесткая. Расчетная схема и действующие силы на нее приведен на рис.1.

При рассмотрении поперечных колебаний сложного узла и баковых труб расчетную схему можно представит как систему с одной степенью свободы, а за основной параметр, описывающий движения, принятъ относительное поперечное перемещение центра масс сложного узла y(t) и все остальные перемещения и силы выразитъ через него.

Силы инерции массы тт и Му3 зависят от абсолютного поперечного перемещения у(t), а силы упругого взаимодействия только от относительного поперечного перемещения y (t) [1].

Основные силы действующие на него показаны на рис.1. Эти силы можно выразитъ через относителъное поперечное перемещение центра масс сложного узла

ỹ(t) следуюшим образом:

ỹ(t) = у(t) – u o (t)

Силы инерции для трубы :

F^т н = m т · ¹ у(t);

Силы инерции для сложного узла : ^уз      у F зн = M^уз·y(t)

Силы взаимодействия трубы с окружающим его грунтом:

Т

F K = S T · ¹ ·k·ỹ(t)

Силы взаимодействия сложного узла с окружающим его грунтом:

^уF^з к =(S^ц у · з k+2·S^ос·K x ) ·ỹ(t)

Силы затухания подземного сооружения и окружающего грунта не учитываем, так как их влияния на максимальний реакции в начальный стадии сейсмического колебания подземных сооружений не существенны. Наша цель определения максимальной реакции сложного узла подземных сооружений при землетрясениях.

Составляем сейсмодинамические уравнения равновесия сложного узла подземных сооружений с учетом (2),(3), (4)и(5):

2·m T · ¹ ÿ(t)+M^уз ÿ(t)+2·S T ^k ỹ у ( з t)+(S^Ц· у k з +2·S^ос·k x ) ·ỹ(t)=0

Подставим (1) в (6):

m T ·(у(t)+U_t o (t) )^//+ M^уз ( у(t)+ U o (t) )^//+ S T ·k·ỹ(t) +                        (7)

(S уз ·k+2·S ос ·K x ) · ỹ(t)=0

Или

(m T +M^уз)·ÿ(t)+[S уTз ·k+S^Ц· у k з +2·S^Ц·k x ]ỹ(t)=–(m T +M^уз) ·Ü o (t)              (8)

ti . (О

Рис 1.

Решений уравнения (8) при нулевых начальных условиях выражается интегралом Дюамеля:

ỹ(t)=– 1

У Р

t

| U o ( Т )^sinp y ( t- Т )dT

o

Таким образом, на основе динамической теории сейсмостойкости сложных систем подземных сооружений [1], получено уравнение позвольяющее количественно оценить поперечное перемещение сложного узла и баковых труб при землетрясениях.

При трубопроводах небольшого диаметра и толщины удаленных от сложного узла сечениях, их относительные поперечные перемещения очень незначительны и ими можно пренебречь [1], Но при трубопроводах большого диаметра и толщины, их относительное поперечное перемещение очень заметно и не учет этого фактора приводит к неверным результатам.

Для численной иллюстрации предлагаемого подхода, в качестве модели землетрясения примем компоненты С-W, акселерограммы Газлийского землетрясения [2].

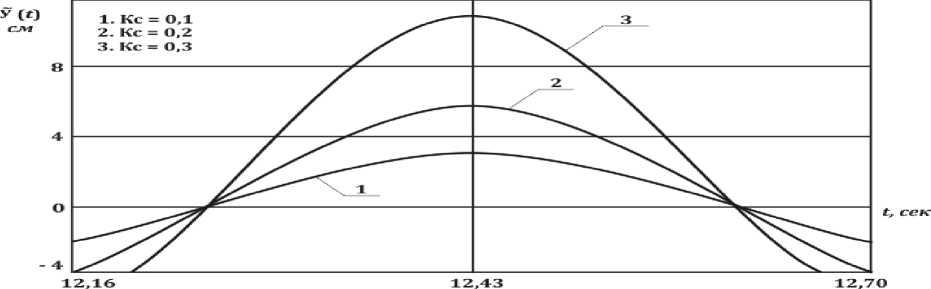
Рис 2.

Изучалось реакции рассматриваемой системы “СУ–СТ”, при этом принимались следующие исходные данные:

ρ=4,2·10^-3кг/см³, R тн =30 см , R тB є[20÷29] см , R kн =100 см ,

R kв Є[70÷95] см , Lє[100÷600] см , Нє[100÷400] см , L 1 ė[10÷50] см .

Результаты численного экспримента на ЭВМ при действии акселерограммы Газлийского землетрясения приведены в виде графикoв изменения реакции ỹ(t) в зависимости от балльности землетрясения [Уразалиев Фахриддин Бахритдинович, Хусниддин Абдухамидович Айнакулов, Ортик Турсунович Назаров. "Исследования реакции сложного узла подземных сооружений при землетрясий как система с одной степенью свободы." Инициатива в образовании: проблема знания в современной науке . 2019. 328-332.].

Из этих графиков видно что с ростом балльности на единицу реакции сложного узла удваивается т.е. прогиб конца стыкуемой трубы к сложному узлу с ростом балльности землетрясения и на влияния других параметров сложного узла (рис.2.) удваивается, чего подвреждает результаты наружного наблюдения разрушения сложных узлов подземных сооружений после силных землетрясений [ 1 ].

"Экономика и социум" №2(93) 2022