Исследования решений сингулярно возмущенных дифференциальных уравнений

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                        

В работе собственные значения матрицы имеют вид Л (t ) = t + i . С помощью параллельных прямых исследуем эти собственные значения и получим оценку включающих особо критической точку. Цель исследования. Доказать асимптотическую близость решений сингулярно возмущенных дифференциальных уравнений и соответствующих невозмущенных уравнений, в случае смены устойчивости на основе конкретного примера.

Материалы и методы исследования

Работа состоит из двух частей:

а). Рассмотрим задачу

£ x ' ( t , £ ) = Л ( t)x(t, £ ) + £ [ g(t ) + f ( t , x ( t , £ )]

x ( — 1, £ ) = x⁰ ( £ ) , | x⁰ ( £ )| = O( £ )

где 0 <  £ - малый параметр, t e [ t ₀, T ] = [ - 1;1 ] , x ( t, £ ) - искомая неизвестная функция.

Для решения правой части поставленной задачи (1) требуется выполнение следующих условий:

U1. g ( t ) , f (t , x ) e Q ( H) - пространство аналитических функций в области Н , f ( t ,0) = 0 , | f ( t ,~) - f ( t , ~)| <  M x x - ~|, 0 <  M - некоторая постоянная.

U2. Л ( t ) = t + i , Re Л ( t ) = t <  0 , -®< t <  0 ; Re Л ( Т₀ ) = 0 , T = 0 , Re Л ( t ) = t >  0 , 0 <  t <  +® .

Имеет место следующая теорема:

Теорема 1. Пусть выполнены условия U1-U2. Тогда V t e [ - 1;1 ] решение задачи (1)-(2) существует, единственно и для него справедлива оценка

Ix (t, £)| < С £ где С - const.

Доказательство. Задачу (1)-(2) заменим интегральным уравнением

t

t

t

x ( t , £ ) = x ⁰

( £ ) exp ¹ j Л ( s ) ds I + j exp ¹ j Л ( s ) ds • [ g ( t ) + f ( t , x ( t , £ ) ] d I £ - 1         J - 1     I            J

t

Для доказательства существования решения уравнения (4) применим метод последовательных приближений.

Последовательные приближения определим следующим образом:

x 0 ( t , £ ) = 0 ,

t

\

t

t

x_n ( t , £ ) = x ⁰

t   tt

^{( £ )ex} p - J ^{Л ( s} ) ^{ds +} J exp j ^{Л ( s} ) ^ds • [ g ^{( t} ) + ^{f ( t}

k£ -1        J   -1    k £t         J

, x_n - j ( t , £ ) ] d T

где n e N .

Далее будем считать, что t = 11 + it2; t = T1 + iT2, где tj, 12, T1, t2 — действительные переменные. Тогда получим j Л(s)ds = j Л(s)ds = (t+ 7^---Q+1L, u(t ,t ) = Re j Л(s)ds = — [t2 - (t2 +1)2].

t 0             -                       ^{2                                            2}

Рассмотрим область H_o = {( t j; t ₂)■ u ( t i, t ₂) <  0 } • Пути интегрирования выберем так, чтобы имело место неравенство

u(11,12) < u(T1T2), от начальной точки до конечной точки (tj, t2). Главное требование на выбор путей интегрирования для последовательных приближений.

Область Н_о делим на две части: H_o = H и H 2 , где H i = {( t i ,1 2 ) e H ₀, — 1 <  1 1 <  0 } и

H 2 = {( t i , 1 2 ) e H о ,О <  1 1 <  1 } .

Определим убывающие пути интегрирования для области H , l = l0 и Zj и l2 и l3, где

1О = {(т1,Т2 ) Т2 = Т + 1 - 1 < Т < 0},

• ¹ 1    = ^{{( т} 1 ^{, Т} 2 ) ^Т 2

• ¹ 2    = ^{{( т} 1 , ^Т 2 ) ■ ^Т 2

• ¹ 3    = ^{{( т} 1 ^Т 2 ) ■ ^Т 2

= —т +1, — ^ > т ^ о},

= —т — 1 — £, — — да < т < —(t2 +1 + £^

= t2,—(t2 +1+V^) < т < ti }•

Во всех выше указанных путях интегрирования условие (6) выполняется и пути интегрировании остаются неизменными для всех последовательных приближений.

Из (5) оценим последовательные приближения на замкнутой области H .

t

t

t

% ! ( t , £ ) = x ⁰ ( £ )exp ¹ | й ( s ) ds + j g ( t )exp ¹ | д s ) ds d r .

I £ —1        J   —1          I £T        J

Здесь Re j ! ( s ) ds =   [ t 1² — ( t ₂ + 1 ) ² ] = u ( 1 1 , 1 ₂) <  0 при ( t_Y , t ₂) e H_o = H и H ₂.

t

A

Поэтому | П ( t , £ )| =

x ⁰( £ )exp ¹ j A ( s ) ds = O £ ) при (^, t ₂) e H

Г £ —1        J

. Остается оценить

t

t

величины I ( t , £ ) = j g ( t )exp -p( s ) ds d r .Предположим, что g ( т ) = O (1) при (^, t ₂ ) e H

—1          Г £T        J

0 •

Тогда I ( t , £ )| = O (1) j exp | — ( u ( 1 1 , 1 ₂) — u ( T 1 T ₂) ) || d T , где 1 = 1 ₀ и 1_X и 1 ₂ и 1. i    ^{Г £                      J}

3 .

• 1) . Будем оценивать величину

  j ^exP

  
  

— ( u ( t j , t ₂) — u ( t , T ) ) l' d T • £                  J

Пусть Zo = {(t,t2)т2 = т +1, — 1 < т < 0}.

Тогда u ( t 1 , t 2 ) ^— u( Г^Т 2 ) =2 ^{[ t 2} — ^{( t} 2 ⁺ ^ — ^T1 ^{+ T} 2 ⁺ 1 ) ^] =2 ^{[ t 2} — ^{( t} 2 ⁺ ^ — ^{T +(}T 1 ^{+ 2 ) ]} =

= ~^{[ t} 12 ^{— ( t} 2 ^{+ 1 ) 2 + 4 т} 1 ^{+ 4} ] .

Вычисляя интеграл, получены оценка

f exp I — (u(tj, t2)—u(т ,T )||dr\

Г £                  J

u ( t ,, t ₂) <  V2exp I    ^{1 L}^

Г£

I j ^exp

— I

2^^+^ 1 dT1 = O(£) .

Г £ J

• 2) . Рассмотрим интеграл

[ exp | —( u ( t_{ , t ₂) — u ( t , T ))r d T .

X £                   7

^l 1

Здесь 4 = {( t , T ) : t₂ = — t + 1, — да> T >  0 } . Путь интегрирования ^ возрастающий.

Нам нужен обратный путь. Следовательно, нужный нам путь будет убывающим. Тогда

^{u ( T} 1 ^{, T} 2 ) = ^— ! ^T 1^{2 —(}T 2 ^{+ 1 ) 2 ]}= ^{— 1 T} 1

Пусть b — const, — да < b < 0. Тогда f exp | —(u (t[, t2) — u (t ,T ))|’ dT = ^

X £                   7

l 1

— (— T + 2) ] — — 2 t + 2.

2 exp

7 u ( t_x , t ₂) Y b’   7 2 — 2 t L

—1—— I exp I1 I dT .

X £   7 Jo    X £   7

Здесь оценка от величины b не зависит. Таким образом, вычисляя интеграл, получим оценку

J ^exp

7 u ⁽ t i , t 2 ) ^— U ( T^T 2 ) X

X

£

| dT = O(£).

3). Теперь вычислим интеграл J exp l 2

7 u ⁽ 1 1 , 1 2 ) ^— u ^{( T} i T 2 ) X

X

l 2 = {T1,T 2 ) :T 2 = —T — 1 — ^, — да< T1 -

£       7

— ( t 2 + 1 + S )} ,

• d T где

^{U ( T} 1 ^{, T} 2 ) = ^— ^X ^{— (}T 2 +

-

1 Г ₂

2 U ¹

-

(- T - £)2 = 1 [2 j£T1 + 4

Пусть - да <  b <  0 , b — const . Поэтому

—

- ( t 2 + 1 + -J~£ )

J    ^exp

— b

u ( t j, t ₂) — u ( t , T )

£

u ( 1 1 , 1 2 )

£

—

■ (t 2 + 1 + ~/~£ )

J    ^exp

— b

£T1 + £ "

X 2£

^d T .

Таким образом, вычисляя интеграл, получена оценка

J exp l 2

( u ⁽ t i , t 2 ) ^— u ( T^T ₂)^Л

X

£

• dT = о (V£). 7

• 4) . Остается вычислить интеграл

  J exp

  l 3

  Здесь l₃ = { ( t , T ) T = t ₂ ,— ( t ₂ + 1 +

  
  

  7 u ⁽ 1 1 , 1 2 ) ^— u ^{( т} ₁₅ Г 2 ) X

  
  

  X £

  ^{£ ) - T} 1 ^- t 1 ( ,

  
  

  • | d r |. 7

  
  

^u ( t 1 , t 2 ) ^{— u} ( ^T 1 ^{, T} 2 ) = ^{1 [ t} 1^{2 — T} 1^{2 ]-} t 1 ^{( t} 1 ^{— T} 1 ) = t 1 ( t 1 ^{— T} 1 ) .

Получен следующий интеграл

71/,

J exp — ( u (^, t ₂) — u ( t , T ) I’ d T - J exp

1 3      ^{X £                           7}           1 3

Рассмотрим два случая:

1*). Пусть ^ < — £ , , тогда

—

£

T ^

I • dTi .

-

£

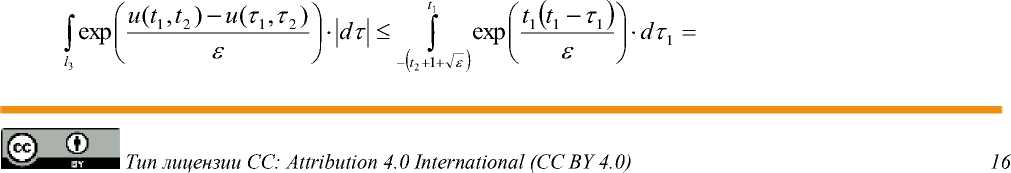
- exp t 1 _

t 1 ^{( t} 1 - ^T 1 )

t 1

£

- — ( 1 2 + 1 +V £ )

£ t 1

exp

t 1 ⁽ t 1 ⁺ t 2 ^{+ 1 +} 4 ) )

к

£

-

1 = O ( £ ) .

2*). Случай — 4 s <  t₁ <  0. Тогда будем иметь

J exP l3

u ⁽ t 1 , t 2 ) - u ^{( T} 1 ^{, T} 2 )

£

t 1

t 1

l| d^ = O (1)   J

— ( 1 2 + 1 + £ ) )

exp

-

T1

к 2£ 7

• d T .

Пусть ^4= = s . Тогда

V 2 £

T = 4 2 ss , d T = 4 £ dds , T 1 = 1 1 , S j

^s ]                              +®

42s J exp (— s2 )ds < 42s J exp (— s2 )ds =

s 2

— T

2£ ’  1

4 2£П

.

.

+m

Учтено, что

— —(t2 + 1 + 4) ) S

—

t^ + 1 + V £

2£

.

интеграл Пуассона j exp ( — s ² ) ds =--- . В итоге получена оценка

0—2

^f u ( 1 1 , 1 2 ) — u Т 1 , т 2P

J exp l3

к

£

• | d ^ = O ( 4s ).

Таким образом, имеет место оценка, если ( t j, t ₂) е H , то

I Х 1 ( t , £ )| <  C4s ,

где 0 < C — const.

Если t , t ₂) е H ₂ то I — l₀ о ~ о l₂ , где

• 1    = {(т1,т2 ) :Т2 = Т1 + 1 — 1 < Т1 <+Ч,

l = {Т, т): т = т — 1—4s,+^ > т > t2 +1+4s}, 1 ={(т1,Т 2 ) :Т 2 = t 2, t 1 > T1 > t 2 + 1 + 4s}.

• 1.1) . Будем оценивать интеграл

[ exp |-( u (^, t ₂) — u ( t , T ))r d T .

к £7

^l 0

Пусть b — const , 0 <  b < +ю и l₀ = {( т , T ) : т₂ = T + 1, — 1 <  т < +® } .

Тогда u (ty, t2) — u (т,t2 ) — — [t| — (t^ +1) + 4^+ b f 2т + 21 exp |I dT .

— 1     к ^£    7

Таким образом exp | —(u (tj, t2) — u (t ,T )||dT < V2 exp к £7

^l 0

Здесь оценка от величины b не зависит. Таким образом, вычисляя интеграл, получим оценку f exp | —(u (tj, t2) — u (t ,T ))r |dT = O (£).

к £                  7

1.2). Рассмотрим интеграл

J exp I ¹ ( u ( 1 1 ,1 ₂) - и ( т^т ₂) ) |- \dr\.

H     <  ^s                    J

Здесь l = { ( т , t ) : т = т - 1 - V s , + да >  т >  t ₂ +1 + V s } . Пусть b - const , 0 <  b < +^ .

Тогда

f exp |— ( u ( t j, t ₂) - и ( т , T ) ) ' W =

~ v s                    J l1

r- (и ( t. , t ₂ )^ b       ⁽ 2 Jst, - s ,

V2 exp I          I J exp-- -J---- d T i .

V ^s J 1 2 + 1 + W     I       ^{2 s} J

Получим оценку exp I — (и (tl, t2) ~ V s l1

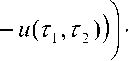
|d^ = O (V s ) .

1.3). Остается вычислить интеграл

[exp ⁽ u ^{( 1} 1 , t ² )   u ^{T 1 , T 2 >} ]• d T

~3  4          s         J '   '

Здесь

^l 2 =^{{ ( t} 1^{, T} 2 ) ^{: T} 2 = * 2 , 1 1 >  ^T 1 >  1 2 + ¹ + V s } ,

^{U (} 1 1 ,1 2 ) ^{- u ( t} 1 , ^T 2 ) = ^{1 [ t} 1^{2 - T} 1 ] ^ t 1 ^{( t} 1

^{- T} 1 ) = ^- t 1^{( t} 1 ^- t 1 ) .

Получен следующий интеграл

J exp I — ( и ( t [, t ₂) - и ( т , T )r V T - J exp l ₃     ^s                     /        ~

~

(_ t 1 ^T t 1 ) 1 d T .

V      ^s J

Рассмотрим два случая:

1.1.1). Пусть tj > Vs , тогда jexp|U(tJЛ)U(T1,т2)\^т - J exp(- t1T -t1)I-d^ = i3     V          s          J         12 +1+4s    V       s     J

s

t 1

exp

V

t 1 ^{( t} 1 ^- s

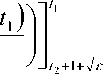
s t 1

I exp

V

t 1 ( t 2 ^- t 1 ^{+ 1 +} d V )

- 1

= O ( s ).

1.1.2). В случай 0 - t j - V s , будем иметь

‘ 1                      _2

^{U 1,2} ---——1 , ’  || d T = O (1)  j exp —— • d T .

,                ^s          J             t 2 + 1 + 4s    V   ^{2 s} J

T

Пусть —= = s , тогда

V 2 s

I---    1 I--- ,                  t                             t 2 + 1 + W

T = 2 2 ss , d ^ = Sdds , т = t_r , s, = —=, т = t ₂ + 1 + д/ s s 2 =---/=—

V2 s                      V2 s

s 1                              +X

V2 s J exp ( - s ² ) ds - V2 s J exp ( - s ² ) ds =

s 2

V 2 sn

В итоге получена оценка

f exp ^{( и (} 1 1 , 1 ₂) ^и (W 2 ) | - | d T = O ().

1:     V s J

Таким образом, имеет место оценка, если (^, t ₂) е Н ₂, то

I X1(t, s)| < C^8 , где 0 < C - const.

Если ( t j, t ₂) e H _o, то учитывая оценки (7) и (8) имеем

|X,(t, s)| < C8, , где 0 < C - const

.

Теперь рассмотрим сходимости последовательных приближений. В дальнейшем, положительные постоянные величины, которые в рассуждениях существенной играют, и поэтому обозначим их одной той же буквой C . Тогда роли не

I x 2 ( t, s ) - X j

( t, s ) < ( c s ) ² .

Далее, имеет место оценка

| x n ⁽ t , ^s ) ^- x n - 1

( t , s )| < ( c s n ) ⁿ , ( n = 1,2,... ) .

Из (9)-(11) при условии ^{Сл/ s} < ¹ следует, что последовательность функций области H равномерно сходится к некоторой функции ^{X (} t , ^s ) ^e Q ⁽ H ) , которая

^X n ⁽ t , ^s ) _R

в

является

решением (4). Единственность решения обеспечивается условием U1. Теорема доказана. б). Рассмотрим задачу sx'(t, s) = D (t) x (t, s) + s[h (t) + f (t, x (t, s ))],

где ⁰ <  ^s

—

D ( t ) =

\

t + i

01 t+i j

X ( - 1, s ) = X ⁰ ( s ), || x⁰ ( s )|| = O ( s )

малый параметр, t ^{e [ t 0} , T ^{]  [ 1;1 ]}   ,    ^{h (} t )    ^{colon ( h} i⁽ t ), ^h 2⁽ t ))   ,

, x ⁽ t , ^s )   colon ⁽ x ^{1 (} t , ^{s )} , x ^{2 (} t , ^{s ))} — искомые неизвестные функции.

~

U1.1.

f ( t ,0) - 0

,

^h ( t ) , ^{f (} t , ^X ) ^e Q ⁽  ) — пространство аналитических функций в области H ,

II f ( t ,~) - f ( t ,~)|| <  M x| x - ~

, 0 <  M — некоторая постоянная.

U1.2. Пусть выполняется условие U2.

Имеет место следующая теорема:

Теорема 2. Пусть выполнены условия U1.1-U1.2. Тогда V t e [ - 1,1 ] решение задачи (12)

(13) существует, единственно и для него справедлива оценка

IIX(t, s)|| < C „ , где C - const.

Доказательство. Задачу (12)-(13) заменим интегральным уравнением

X ( t , s ) = X ⁰

M t.              1     t.            t.

^{( s )} exp I - J D ⁽ s ) ds l + J exp I - J D ⁽ s ) ^ds l^[ h ^{( т} ) + f ^{( т} , x 0 , ^s )) d

t

t

t

k

т ,

k

-

-I

k

т

Для доказательства существования решения уравнения (15) применим метод последовательных приближений. Последовательные приближения определим следующим образом:

x o ( t , s ) = 0,

t

\

t

t

\

X n ( t , s ) = x⁰

( s )exp ¹ J d ( s ) ds + J exp ¹ J d ( s ) ds • [ h ( t ) + f ( t.

Is0       J       IsT       J

, X n - 1 ( t , s )) ] d T ,

где x_n ( t , s ) = colon ( x 1 _n ( t , s ), x _{2 n} ( t , s ) ) , n e N .

Если ( t j, t ₂ ) e H _o, то аналогично определяя область, выбора путей интегрирования и проводя вычисления по вышеуказанному в скалярном случае для первого приближения имеем оценку

II x/ 1 , s )|| <  C s ,

где 0 < C — const.

В дальнейшем, положительные постоянные величины, которые в рассуждениях существенной роли не играют, обозначим одной той же буквой C . Тогда

II x 2 ( t , s ) — x j ( t , s )|| <  m J || x i ( t , s )|| exp ( u ⁽ t 1 , t ² )    ^{u ( T 1 , T 2} ) ] • I d T <

i              V         s         J

< MC W J exp I u(t 1, t2) u(T1,T2) | • dT < (c s) )2

i     v          s          J

Получим

II x 2 ( t , s ) — x j ( t , s )|| <  ( c V s ) ² .

Далее, имеет место оценка

II x n ( t , s ) — x n — 1 ( t , s )|| <  ( c V s ) n , ( n = 1,2,... ) .

Из (17)-(19) при условии ^{C s} <  ¹ следует, что последовательность функций ^x n ⁽ t ’ ^s ) в области H равномерно сходится к некоторой функции ^{x (} t ’ ^s ) ^e Q ⁽ H ) , которая является решением (15). Единственность решения обеспечивается условием U ^1.1. Теорема доказано.

Результаты и обсуждения

В работе на основе рассматриваемого классического примера для одного собственного значения матрицы провели вычисления нового способа. В новом способе выбора путей интегрирования коренным образом отличается способам выбора путей интегрирования в работе [1]. В итоге получается не улучшаемая оценка. Пути интегрирования для всех последовательных приближений остаются неизменными.

Вывод

Используя основные понятия проективной геометрии создан новый способ для исследования решений сингулярно возмущенных дифференциальных уравнений. Как преимущество можно считать, что пути интегрирования для последовательных приближений остаются неизменными. А также направление вычислений. Если собственные значение матрицы остаются комплексно сопряженными, тогда в некотором случае появиться ограничение области. Остается, проверить этот случай. Об этом объявим в следующих исследованиях.

Как преимущества способа можно считать, что для кратных собственных значений, а также для действительных собственных значений применим этот способ.