Итерационная факторизация на фиктивном продолжении для численного решения эллиптического уравнения четвёртого порядка

Рассматривается эллиптическое дифференциальное уравнение четвёртого порядка в прямоугольнике со сторонами, параллельными осям координат, на двух смежных сторонах прямоугольника заданы условия шарнирного опирания, а на остальной части границы условия симметрии. Для дискретного аналога этого уравнения в виде систем линейных алгебраических уравнений приводится факторизованный предобуславливатель квадратно попеременно треугольного вида. Исходная задача может быть получена в методах типа фиктивных компонент при решении эллиптических дифференциальных уравнений четвёртого порядка в плоских областях достаточно произвольного вида при однородных главных или естественных краевых условиях.

Из линейной теории изгибания тонких пластин на упругом основании, основываясь на [1, 2] энергия деформированной пластины может быть записана в виде

E(й) = 1D J ((АЙ)2 + 2(1 - a)(йxy - йийyy))dQ +1J Kit2dQ - J PйdQ, 2Ω2ΩΩ где P – давление, K – коэффициент жёсткости упругого основания (K ≡ 0 в случае отсутствия упругого основания), D=Eh3(12(1 -σ2)) – цилиндрическая жёсткость пластины, h – толщина пластины, E – модуль Юнга (модуль растяжения), σ – коэффициент Пуассона (отношение поперечного сжатия к продольному растяжению), Q - плоская область, й - искомое смещение. Если приравнять к нулю вариацию энергии t-x                  t-                            t- t-        t- t-        t- t-                                                 't'

δE(u) = D∫(ΔuΔv +(1-σ)(2uxyvxy -uxxvyy -uyyvxx))dΩ+∫KuvdΩ-∫PvdΩ=0,

ΩΩΩ где v = 5й, то при a = K/D, f = P/D получается, что

[ (о-Аit Аv + (1 - a )( й_хxv_xx + 2 й_хvv_xv + й_хv _v) + ai t ) d Q = f ^d Q . xx xx xy xy yy yy

ΩΩ

После интегрирования по частям устанавливается ds - J12itvds = J fvdQ, sΩ

[ (А ² й + ай') vd Q + [ 1 1 й—

∂ n

Ωs где li й = А й +(1 - °) ni n 2 йxy - n 2 йxx - ni2 йyy,

, „ дАи          . д .     .„

-

й xx ) + ( n 2 - n 22 ) It xy ),

l ₂ u =     + (1 - σ ) ( n ₁ n ₂( u _yy

∂n∂s s =∂Ω, n1 =-cos(n, x) , n2 =-cos(n, y) .

Таким образом, возможно рассмотрение краевых условий жёсткой заделки, шарнирного опирания, симметрии и свободного опирания в отдельном или смешанном виде.

Непрерывная рассматриваемая задача в вариационной и классической постановках

Рассматривается задача

• - е V,: Л(й,,ч) = g,(Ч) Vv, е V,, g е V(1)

где соболевское пространство функций

• V , = V , ( Q ) = | v , е W ₂²( Q ): 4 |_r = 0, I = q |

I                     11

на области Q = (0;b,)x(0;b2), с границами Г, ={b,}x[0;b2]U[0;b,]x{b2},Г2 =г\г1,Г = дQ, билинейная форма '- '-                                                          '- ■-                                                                ■- ■-                                   ■- ■-                           ■- ■-'

^{Л (} u i , ' Ж = J ^{( a A} u i A ^V 1 + ⁽¹ - a ⁾⁽ Uxx V xx + ² Uxy V xy + u yy V yy ) + au , v , ) d ^Q ,

Q при этом a = a, на области Q,, a = a2 на qXq, , области Q,, Q2: Q = Q, U Q2, Q, П Q2 = 0 , dQ, П dQ2 ^0 , заданы константы ае (0;1), b,-,b2 е (0; +~), a,-,a2 е [0; +~), a, < a2.

Можно отметить, что

• ^- II²             /^{- -} II^- II²         -^

³ c , ,c 2 ^е( 0; H^: c 1lЫ W ₂ 2 ( q ) <^{л ( v}„^v , ) < c 2Il ^v 1l W ₂ 2 ( q ) ^{v v} , ^е V , , а, следовательно, решение задачи (1) существует и единственно. Если й, - искомая, а f , - заданная достаточно гладкая функция и

. ( ^- , ) = ( Л , V , ), где ( Л , , ^- , ) = J Л ^- , d Q ,

Q то из задачи (,) получается неоднородное бигармоническое уравнение со свободным членом при смешанных и однородных краевых условиях

* 2 - . - ^- -I                     d й I       dA й , 1

A u, +au, = f, , u, г =Au, г =0,      Г2 = -X Г2= 0.

• ^{1    1            11} d n ^{1 2} d n ²

Дискретная аппроксимация рассматриваемой задачи

Производится дискретизация задачи (1) по методу конечных элементов на параболических восполнениях: ---- й, е V, с V,: Л(й,,V,) =.-,(V,) VV, е V, с V,.(3)

Рассматривается система линейных алгебраических уравнений, соответствующая задаче (3):

й, е ЖN : Лй, = g,, g, е ЖN,(4)

где V , е Ж N : v , = ( v ,,, ,..., v ,, N )', N = m • n , m , n е N , а V ,n ₍ i _{- 1) +} j = V 1, , , j , i = 1,..., m , j = 1,..., n , и V 1, , , j являются значениями функции дискретного аргумента соответствующего узлам сетки ( x _t , y j ) = ( ( i - 0,5) h , ,( j - 0,5) h 2 ) , i , j е X , шаги сетки h , = b , /( m + 0,5), h ₂ = b ₂/( n + 0,5), состоящей из указанных выше узлов, а матрицы Л размерности N x N , определяются следующим образом:

(Л й , , V ,) =Л ( й , , V , ) V й , ,V , е V , с V , , здесь (.,.) - скалярное произведение векторов следующего вида:

N

(й„V,) = (й,,V,)h,h2 = ^u,,kV1,kh1 h2 Vм,,v,е ЖN, k=, а подпространство V, с V, определяется так, что m n

• V ,    =

• ^V 1 ^{:    V} 1

= ЕЕ ^v 1, i , j ^{ф 1} ’ j ^{( x} , y ), ^v 1, i , j ^{е Ж} , r , i = 1 j = 1

где базисные функции

Ушаков А.Л.

Итерационная факторизация на фиктивном продолжении для численного решения эллиптического уравнения четвёртого порядка

Фi,j(x,y) = V1,.(x)V2, j(y), y^.(x) = E(1/i)V(x/h1 -i + 3) + V(x]hx -i + 2)-E(ijm)V(xjh1 -i), m , j = 1,...,n ,

V 2, j ( y ) = E (V j ) V ( y/h - j + 3) +V ( y/h 2 - i + 2) -E ( jin ) V ( y/h 2 - j ) , i = 1,

0,5 z ²,             z e [ 0;1 ] ,

V ( z ) = X z ² + 3 z - 1,5, z e [ 1;2 ] ,

0,5 z ² - 3 z + 4,5, z e [ 2;3 ] ,

V(z) = 0, zё [0;3], E(.) - функция целая часть числа, компоненты вектора g1 определяются сле дующим образом:

g 1, n ( i - 1) + j = g 1,i , j = h 1 ^{- 1} h 2 ¹ g 1 ( Ф ^{1 ,} j ( x , y )), i = 1,..., m , j = 1,..., n , т.е. gg_vv ^ = ^C i ^i), V v e Г_г Отметим, что решение задачи (4), как и (3) существует, единственно и известны оценки типа

¹ I K - ^U 1| W ₂ ^k (П) ^{- C}|h |    IKI W 2(Q) ^,

• ²    Й^ К ^{- U} 1I W 2 ² ( Q ) = ^0, h = ^{( h} 1 ^{, h} 2 ^), h\ = ^max { ^h 1 ^{, h} 2 } .

Выбирается фиктивное продолжение дискретной решаемой задачи из (4)

U e Ж ² N : DU = g , g e Ж ² N , g ₂ = 0,                          (5)

где векторы v e Ж2N : v = (v ', v ')‘, \ 1 , 2      , блочная, нижнетреугольная матрица D размерности 2N x 2N такова, что -2

^D 11 = ^Л , ^D 12 = ⁰ , ^D 21 = ⁹ A , ^D 22 = M 9 , матрицы

9 = A9 + 9A, Me = A2 - 92, 9 = V/Vv-VvX, A = VxX+VvX, A                J 9               J x y y x J x x y y J а матрицы Vx, Vy размерности N x N определяются следующим образом (a = 1,2):

(VxUa,va} = ££(-(ua,i+1,j -Uai,j)h-vai,j)h1h2, ua,m+1,j = va,m+1,j = 0 j = X,•••,n, i=1 j=1

(^V y ^U a ^,v a) = ££ £ ^{( - ( u} a , i , j + 1 ^{- u} a , i , j ) ^h - ^{1 v} a , i , j ) ^h 1 ^h 2 ^{, u} a , i , n + 1 = ^v a , i , n + 1 = ⁰ i = ^X,•••^{, m} .

i = 1 j = 1

Введём подпространства векторов:

V = { v = ( v ₁ ‘ , v 2 ’ ) ‘ e Ж ^{2 N} : 9 a Y 1 + M 9 v ₂ = 0 } , V 2 = { v = ( v ₁ ' , v 2 ’ ) ‘ e Ж ^{2 N} : v ₁ = 0 } .

Утверждение 1. Решение задачи из (5) U = ( U V, U ^ ) ‘e V ₁ существует, единственно и U ₁ - решение задачи из (4).

Итерационная факторизация на фиктивном продолжении дискретной решаемой задачи Определим блочную матрицу (2 размерности 2 N x 2 N такую, что ^.          ^.                        ^.                         ^.

C 1 1 = C 22 = ^M 9 , ^C 12 = ^{- 9} A , C 21 = ⁹ A .

Для решения задач из (5) предлагается итерационный процесс:

U^k e Ж ^{2 N} : ( 2( U^k - U^{k - 1}) = - т_к ( D) U^{k - 1} - g ), T _k >  0, k e N V U ⁰ e V ₁ .              (6)

Заметим, что в итерационном процессе из (6) возникают задачи с факторизованным оператором следующего вида:

U e С ^N : ( LL* )² U = G , G e С ^N , при этом возможно расщепление на более простые задачи

H e С ^N , LH = G , G e С ^N , W e С ^N , LW = H , H e С ^N ,

Q e C N , LQ = W , W e C N , U e C N , LU = Q , Q eC N , где матрицы L и L удовлетворяют следующим соотношениям ( ё^г = - 1):

l = v,'-evy', L= L'=v, + evy, lL = (v,‘-evy')(v, + evy) = a+eo,

( LL )² = ( A + e O ) = M _o + e O _A , тогда

(M° + О )(u1 + eu2) = gi + eg2, что равносильно системе:

' M o u 1 - ° A u ₂ = ^g i , u 1 + eu 2 = и , ^o A u 1 + M ₆ ^u ₂ = ^g 2 , g 1 + eg ₂ = G и действительно на каждом шаге итерационных процессов из (6) возникают задачи типа 7и = g , u = ( u ’ , u 2 ) ‘ , g = ( g 1 , g 2 ‘ ) ‘ .

Утверждение 2. Если в итерационном процессе из (6) Я k e N : u k ^{- 1} = и , то и u k = и .

Пусть u k = и + у ^k , V k e N U {0}.

Утверждение 3. Для итерационного процесса из (6) выполняется

О у + МОу2 = (1 - Tk) (OA^k-1 + МОу2-1), Vk e N , уk e V1 Vk e N U {0}.

Замечание 1. Имеют место неравенства

Я С 1 , c 2 e (0; +~ ): c M _e < Л <  c 2 M _e [3, 4].

Утверждение 4. Имеет место равенство

(буу) = (Мо^у)-(M°^2,^2) Vуe V1,

2 N где также (u,v^ = (u,v)h1 h2 = ^ukvkh\ h2 Vu,v e >2N.

k = 1

Доказательство. Учитывая, что

° A ^ 1 + M _eV 2 = 0, ° A =^{- 9} a , получается

(( 7 ^ , ^ = ( M o ^ 1 , ^ 1) ^- ( ⁹ A ^ 2 , ^ 1) = ( ^M O ^ 1 , ^ 1) ⁺

+ ^ 2 ° A ^ 1) = ( M ° ^ 1 ^ 1) - ( M o ^2 ) .

Предположение 1. (О фиктивном продолжении действительной части на мнимую часть) Имеет место неравенство

Я ^ 2 e ⁽⁰;1): ( ^м ° ^ 2 ^, ^ 2) <  ^а 2 ( ^M o ^ 1 ^, ^ 1) ^V ^ e V 1 .

Можно отметить ( y = (1 - а ₂) ^{- 1} или а ₂ = 1 - Y ^-1), что

ЯYe (1; +-): (М9^1,^1) < y(C7^,^ = y(( MeV1,V1^- (М^,^)) V^e ^, т.к. матрица M9 > 0 потому, что V ^1 Ф 0

к^M e V 1 , ^ 1) = (^{( A 2 -} ° ²⁾ ^ 1 , ^ 1) = ( ^A 2 ^ 1 , ^ 1) ^- ( ° ² ^ 1 , ^ 1) = кA V 1 , ^А ^ 1) ⁺ °^ 1 , °^ 1) >  ⁰

и матрица ( 7 >  0 , в нашем случае при ^ e V 1 , т.к. выводится, что

( ( 7 ^ , у ) = ( М ₆^ 1 , ^ 1 ) - ( 9 a ^ 2 , ^ 1 ) = (( A ² - ° ² Ж 1 , ^ 1 ) - (( A O + ° A ) ^ 2 , ^ 1 ) =

= ( A ^ 1 )² + ( ⁹^ 1 )² - ( O^ 2 , A ^ 1 ) + ( А У 2 , ОУ 1 ) = ( А У 1 - 9^ 2 ) 2 + ( А У 2 + °у 1 ) >  0, V у Ф 0, последнее потому, что ( v x' - e v _y' )( v x + v _y )( у 1 + <г у ₂ ) Ф 0 V у Ф 0 .

Также можно отметить, что для У e V 1 , т.е. для функций из соответствующего подпространства

Ушаков А.Л.                    Итерационная факторизация на фиктивном продолжении для численного решения эллиптического уравнения четвёртого порядка

∃ λ ^{- 2} ∈ (0; +∞ ): 0 ≤ M _θψ ₂, ψ ₂ = M _θ ^{- 1} θ _A ψ ₁, θ _A ψ ₁ ≤ A ^{- 2} θ _A ψ ₁, θ _A ψ ₁ =

= ( θ + A ^{- 1} θ A ) ψ ₁,( θ + A ^{- 1} θ A ) ψ ₁ ≤ 2 θψ ₁, θψ ₁ + 2 A ^{- 1} θ A ψ ₁, A ^{- 1} θ A ψ ₁ ≤

≤ 2 θψ1,θψ1 + 2λ-2 θAψ1,θAψ1 ≤ 2 θψ1,θψ1 + 2λ-2 θϕ1,θϕ1 →0 , при h1, h2 →0, где ϕ1 = Aψ1 , т.е. Mθψ2,ψ12 → 0, ψ2 → 0 , при h1,h2 → 0 , т.к.

θψ1 =(∇x′∇y -∇y′∇x)ψ1 →0, θϕ1 =(∇x′∇y -∇y′∇x)ϕ1 →0, при h1, h2 →0, по формуле Тейлора, если ϕ1,ψ1 – дискретные аналоги достаточно гладких функций.

Утверждение 5. Имеют место неравенства c1 Cˆψ,ψ ≤ Dˆψ,ψ ≤γc2 Сˆψ,ψ , ∀ψ∈V1 .

Доказательство. Заметим, что c1 Cˆψ,ψ =c1( Mθψ1,ψ1 - Mθψ2,ψ2 )≤c1 Mθψ1,ψ1 ≤ Λψ1,ψ1 = Dˆψ,ψ .

С другой стороны,

γ c ₂ C ˆ ψ , ψ = γ c ₂( M _θψ ₁, ψ ₁ - M _θψ ₂, ψ ₂ ) ≥ γ c ₂(1 - α ₂) M _θψ ₁, ψ ₁ ≥ Λ ψ , ψ = D ˆ ψ , ψ .

Утверждение 6. Если в итерационном процессе из (6)

τk =τ=2 (c1 +γc2) и q=(γc2 -c1) (γc2 +c1), то

ˆ k k 2 ˆ k - 1 k - 1

C ψ , ψ ≤ q С ψ , ψ   , k ∈ ℕ .

Доказательство. Из итерационного процесса получается, что

Cˆ(ψk -ψk-1) =-τDˆψk-1, ψk =Tψk-1 , T =E-τCˆ-1Dˆ , T =T′>0, тогда

C ˆ T ψ , T ψ

C ˆ ψ ^k , ψ ^k = C ˆ T ψ ^{k - 1}, T ψ ^{k - 1} ≤ su p            C ˆ ψ ^{k - 1}, ψ ^{k - 1} =

ψ ∈ V 1   C ψ , ψ

= sup ψ ∈ V ₁

(CT**1

<2 y , ^

к \        /7

C ψ ^{k - 1}, ψ ^{k - 1} = sup ψ ∈ V ₁

((C - tDT >,y}

к

7

C ˆ ψ k - 1 , ψ k - 1 ₌

= su p ψ ∈ V ₁

1 - т

D V , ^

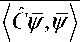
C ˆ ψ ^{k - 1}, ψ ^{k - 1} = max { (1 - τ c ₁)², (1 - τγ c ₂)² } C ˆ ψ ^{k - 1}, ψ ^{k - 1} = q ² C ˆ ψ ^{k - 1}, ψ ^{k - 1} .

Введём норму

v 1 _Λ = Λ v 1 , v ₁ .

Теорема 1. В итерационном процессе из (6), при τk =τ=2 (c1 +γc2) , k∈ ℕ , будет u1k-u1 Λ≤ε u10-u1 Λ, где

0 ≤ ε ≤ γ c ₂ c ₁ q^k .

Доказательство. Из утверждения 5 получается

ψ ^{k 2} _Λ = Λ ψ ^k , ψ ^k ≤ γ c ₂ C ˆ ψ ^k , ψ ^k ≤ γ c ₂ q ^{2 k} C ˆ ψ ⁰, ψ ⁰ ≤

≤ ( γ c ₂ c ₁) q ^{2 k} Λ ψ ⁰, ψ ⁰ = ( γ c ₂ c ₁) q ^{2 k} ψ ^{0 2} _Λ .

Вывод. Учитывая вид матриц L , L ^∗ , можно отметить, что для решения задачи из (4) с N неизвестными, на основании приведенной теоремы 1, предложенными итерационным процессом из

• (6)    с относительной погрешностью ε , требуется не более чем O ( N ln ε ^{- 1}) арифметических операций. Для выбора итерационных параметров τ _k не требуется точного знания констант γ , c ₁ и c ₂ , т.к. для ускорения сходимости итерационного процесса из (6) можно использовать известные вариационные методы и рекомендовать, например, метод скорейшего спуска.

• 1.    Ландау, Л.Д. Теория упругости / Л.Д. Ландау, Е.М. Лифшиц. – М.: Наука, 1965. – 204 с.

• 2.    Оганесян, Л.А. Вариационно-разностные методы решения эллиптических уравнений / Л.А. Оганесян, Л.А. Руховец. – Ереван: Изд-во АН АрмССР, 1979. – 235 с.

• 3.    Ушаков, А.Л. Модификация итерационной факторизации для численного решения двух эллиптических уравнений второго порядка в прямоугольной области / А.Л. Ушаков // Вестник ЮУрГУ. Серия «Математика. Механика. Физика». – 2013. – Том. 5, № 2. – С. 88–93.

• 4.    Ушаков, А.Л. О приближённом решении одной эллиптической краевой задачи четвёртого порядка / А.Л. Ушаков. – Челябинск: Челябинский государственный технический университет, 1997. – 30 с. (Деп в ВИНИТИ 21.04.97, № 1346 – В97).