Итерационная процедура расчета напряженно-деформированного состояния при чистом изгибе балки из материала с падающей диаграммой

The pure bending of a bar made of falling branch material is considered under the monotonic increasing bending moment (rigid loading) or the monotonic increasing curvature of the bar (soft loading). The iteration procedures of the stress-strain analysis taking into account the capability of the material to work at the stage of softening (falling branch) are presented. A relationship between the stability of the deformation process and the convergence of the iteration procedure has been established.

Диссипативные процессы, происходящие в материале при его деформировании, а именно, пластическая деформация и континуальное разрушение, приводят к появлению на диаграмме деформирования падающего участка, который отвечает разупрочнению материала. На стадии разупрочнения материал реологически неустойчив [1, 2]. Учет возможности работы материала на закритической стадии деформирования играет важную роль в расчетах на прочность. Можно выделить два основных аспекта. Во-первых, на стадии разупрочнения материал еще сохраняет некоторую несущую способность и учет этого обстоятельства позволяет обеспечить более точное определение предельной несущей способности конструкции и их элементов, то есть максимально использовать ресурс материала. Во-вторых, появление в элементе конструкции зон с неустойчивым материалом существенным образом влияет на устойчивость процесса его деформирования и разрушения [1].

В данной работе на примере чистого изгиба балки из материала с падающей диаграммой приводится описание итерационной процедуры, позволяющей учесть наличие стадии разупрочнения материала. Показана связь между устойчивостью процесса деформирования и сходимостью итерационной процедуры.

1.    Определяющие соотношения

Рассмотрим чистый изгиб балки с прямоугольным поперечным сечением. Высота балки равна 2 h , ширина - b , длина - L ( L >>  h ). Деформирование осуществляем квазистатически при неизменной температуре, задавая либо монотонно возрастающий изгибающий момент M (мягкое нагружение), либо монотонно увеличивая кривизну балки к (жесткое нагружение). Свойства материала определяет полная диаграмма деформирования a ( е ) , полученная при растяжении. Она обладает восходящей и ниспадающей до нуля ветвями (Рис. 1). Символами a ^r , a B , f , е^в обозначены соответственно предел текучести, предел прочности и отвечающие им деформации; e ^Z - деформация разрушения. Функцию a ( е ) полагаем однозначной и непрерывно дифференцируемой необходимое число раз.

В случае чистого изгиба единственной ненулевой компонентой тензора напряжений является продольное напряжение a x = a ( у ), а продольная деформация e x = е ( у ) линейно распределена по высоте балки (Рис. 2). Считаем, что диаграмма при сжатии симметрична относительно начала координат диаграмме растяжения. В этом случае обеспечивается неизменность положения нейтральной плоскости, на которой продольные напряжение и деформация равны нулю. Отсюда функции a ( у ) и е ( у ) являются нечетными функциями.

Наклон диаграмм характеризует четная функция E^p ( е ) = da)d e , имеющая смысл касательного модуля. Ее знак определяет состояние материала, а именно, при Е^р >  0 материал находится в состоянии упрочнения, при Е^р <  0 - в состоянии разупрочнения, когда возрастание деформации по абсолютной величине сопровождается уменьшением абсолютной величины напряжения.

Наконец, материал считаем упругопластическим. Следовательно, разгрузка происходит по закону упругости с модулем E ( E - модуль Юнга), и полная деформация е = к у аддитивна, то есть е = e e + е ^р , ( е ^е , е ^р - соответственно упругая и пластическая составляющие полной деформации (Рис. 1)). Очевидно, что все составляющие полной деформации также являются нечетными функциями переменной у .

Для упругопластического материала при одноосном растяжении соотношение, связывающее напряжение и деформацию, имеет вид [2]:

a = Е е = E ( е - е ^р ) .

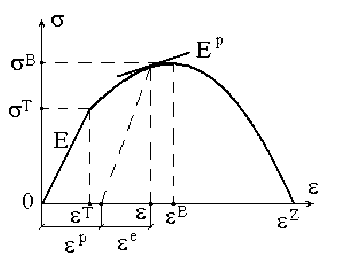
Рис.1. Полная диаграмма деформирования при растяжении

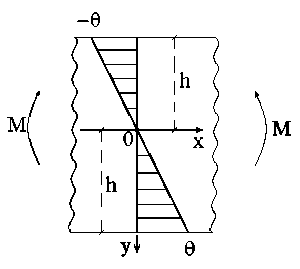
Рис.2. Распределение продольных деформаций относительно нейтральной плоскости;

6 = е ( h ) - деформация наиболее растянутых волокон балки

Это определяющее соотношение должно быть дополнено зависимостью, связывающей полные и пластические деформации. Воспользуемся дифференциальными равенствами do = E (de - dep),     do = Epde.

Приравнивая их, находим связь между дифференциалами полной и пластической деформаций (так называемый инкрементальный закон пластичности [2]):

d e p = ( 1 - E^p ( e )/ E ) d e .

Отсюда получаем выражение для пластической составляющей полной деформации:

e (

e p = J 1

0 к

E^p ( e ) )

d e .

2.    Краевые задачи

Очевидно, что напряжения и деформации при чистом изгибе тождественно удовлетворяют дифференциальным уравнениям равновесия и условиям совместности. Следовательно, требуется только определить такое их распределение по высоте балки, при котором удовлетворяются определяющие соотношения (1) и (2). В случае мягкого нагружения на торцах балки (как и в каждом поперечном сечении) должны удовлетворяться граничные условия

J o dy = 0,       b J o ydy = 2 b J o ydy = M ,                                  (3)

• - h                         - h               0

а в случае жесткого нагружения деформация на нижней (растянутой) плоскости балки должна удовлетворять равенству

9 = K h.

Сформулированные краевые задачи (1), (2), (3) и (1), (2), (4) назовем исходными краевыми задачами.

Отметим, что выражения (3), где первое равенство выполняется тождественно в силу нечетности функции o ( y ) , играют роль статических уравнений равновесия.

Каждую исходную краевую задачу можно разбить на две задачи, одну из которых назовем основной задачей, а другую – корректирующей задачей. Основными являются задачи о чистом изгибе балки под действием изгибающего момента (условие (3)) или при задании кривизны (условие (4)). Определяющее соотношение в них имеет вид o = E e . Решение основной задачи для мягкого нагружения определяется выражениями:

o' = Ek y ,            e = к y ,           к = a M.                           (5)

Для жесткого нагружения имеем:

o = E x y ,            e = K y ,           M' = Xk .                            (6)

Здесь Я - жесткость балки при изгибе, равная 2 Ebh ³/3, а = Я ¹; К - кривизна, отвечающая заданному моменту; M' - момент, отвечающий заданной кривизне.

Корректирующие задачи – это задачи об определении собственных (остаточных) напряжений а "( у ) , возникающих в упругой балке вследствие появления остаточных пластических деформаций £ ( у ) . При этом балка либо свободна от внешних усилий, то есть

h j а * dy = 0,

- h

b j a ydy = 2 b j a ‘ ydy = 0,

hh

- h

либо защемлена, то есть

К = 0.

Определяющее соотношение в корректирующих задачах имеет вид а * = E (e ‘- £), где e ( у ) - линейно распределенные по высоте деформации, определяемые возникшей кривизной балки. Решение корректирующей задачи для граничных условий (7) задаем выражениями a" = EK у - Eep,    e = К у,         К = aMф,

а для условия (8) имеем а" = -E£,          e = 0,           M" = -Mф.                        (10)

hh

Здесь M ф = bE j £p (у) ydy = 2bEj £p (у) ydy фиктивный изгибающий момент;

- h                           0

К - кривизна балки, возникшая в результате появления остаточных деформаций; M - изгибающий момент, необходимый для сохранения нулевой кривизны.

Непосредственно проверяем, что решениями исходных задач при заданной функции £p (у)  являются суммы решений соответствующих основных и корректирующих задач.

3.    Итерационная процедура определения напряженно-деформированного состояния

Пусть балка находится в равновесии. При этом изгибающий момент равен M ₀ , кривизна - к ₀ , полные деформации - £ 0 = К ₀ у , напряжения - а ₀ ( у ) , пластические деформации - £ 0 ( у ) . Деформации и напряжения в каждой точке балки удовлетворяют определяющим соотношениям (1) и (2). Также известно распределение касательного модуля по высоте балки: E ₀ ^Р ( у ) = E^p ( £ ₀ ( у ) ) = E^p ( к ₀ у ) .

Возмутим данное положение равновесия, увеличив изгибающий момент на малую величину M _∆ (мягкое догружение). Для параметров нового положения равновесия M = M ₀ + M _∆ получим выражения: κ = κ ₀ + κ _∆ , σ = σ ₀ + σ _∆ , ε = ε ₀ + ε _∆ , ε ^p = ε ₀ ^p + ε _∆ ^p , где функции σ _∆ ( y ) , ε _∆ = κ _∆ y , ε _∆ ^p ( y ) – решения так называемой возмущенной исходной краевой задачи с определяющими соотношениями

σ _∆ = E ( ε _∆- ε _∆ ^p ) ,

^£ 0 + ^£ д Г

£ 'д = I 1 -

£0  V

Ер(£))

E

d £

)

и граничными условиями

h

J с т _д dy = 0,

- h

h

² b I У д ydy = M д .

Для решения возмущенной краевой задачи воспользуемся следующей итерационной процедурой. Сначала для M _∆ находим решение основной задачи (5):

κ _∆′ = α M _∆ ,              ε _∆′ = κ _∆′ y ,                σ _∆′ = E ε _∆′ .

Так как эти величины не удовлетворяют соотношениям (11), (12), то они могут рассматриваться только как первое приближение к искомому решению. Следовательно, необходима корректировка данного приближения.

Разложим интеграл в выражении (12) в ряд по ε _∆ в точке равновесия ( ε _∆ = 0):

^p ε _∆

¹ - E P T² V E )

1 1 dE^p       2

ε -          | ε

^∆ 2 E d ε ^{ε = ε 0 ∆}

В дальнейшем, вместо определяющего соотношения (12), будем использовать линейный член в разложении (13). Тогда для приращения пластической деформации, отвечающего приращению ε _∆′ полной деформации, получим выражение вида:

p

£1 (У )= 1—Е^ £‘( У) -V E )

Теперь для ε _∆ ^p ₁ находим решение корректирующей задачи (9), а именно,

h

φ                                          pφ           p

Лд1   ам Д1,     eД1   Лд1y , Мд1 ЕКД1y  Е£Д1, M Д1   2 bE J £д1 (y) ydy , и второе приближение

κ _{∆ 1} = κ _∆+ κ _{∆ 1},      ε _{∆ 1} = ε _∆+ e _{∆ 1},     σ _{∆ 1} = σ _∆+ σ _{∆ 1}.

Если соотношения (11) и (12) снова не удовлетворяются, то осуществляется следующая корректировка.

Сначала по деформациям £ 1 ( у ) = £ 0 + £ _Д и диаграмме деформирования определяем касательные модули E 1 p ( £ 1 ) , распределенные по высоте балки. Затем находим приращения пластических деформаций на отрезке [ £ ₀ + £_Д , £ 0 + £ _{Д 1} ] , то есть

p

^£ Д 2

(

V

Ep )

E )

e Д 1 ’

и второе приближение   ^К Д2 = К д 1 ^{+ К} Д2 ,   ^£ Д 2 = ^£ Д 1 ⁺ e Д 2 = ^К Д 2 у ,   О д 2 = а Д 1 ⁺ о Д ₂,  где

h кД2 = аМ ф2,    eД2 = кД2у ,    аД2 = ЕКдгу - E£pp2,    Мф2 = 2bEj £22 (у) уду - решение корректирующей задачи при £ = £Д2. Далее поступаем аналогично. Процесс корректировок продолжаем до тех пор, пока соотношения (11), (12) не будут удовлетворяться с заданной степенью точности.

В результате применения данной итерационной процедуры, в ходе которой кривизна балки монотонно растет, получаем числовой ряд с положительными членами

^

^к д = ^к Д⁺ Е ^К Д , i = 1

где   кД1 = c0кД , „., кД(n+1) = спкДn, .... Коэффициенты ck   (k = 0,1,...) определяет выражение c = 1 -2ba^Ep (у) у2dy = 13— jEp £)£2d£.                               (15)

^Jo                  ^{Eh K} 0

Чтобы получить значение коэффициента c_k , в формулу (15) следует подставить значения j - 1

^E p ( у ) = E kp ( у ) , ^K = к , ^j = ^j k = ^K k h , где ^K 1 = ^K o ^{+ К} Д , ^K j = ^к 1 ⁺ Е ^К Д i ⁽ j - ²⁾ . Ряд ⁽¹⁴⁾ i = 1

сходится, если c_k <  1, и расходится, если, начиная с некоторого номера n = N , коэффициенты c_k >  1 ( k >  N ). Когда ряд сходится, то в пределе получаем искомое решение возмущенной исходной краевой задачи.

Для оценки величины c исследуем знак интеграла к                          , е

J = E E^P ( у ) у ² dy = -3 J e^p ( £ ) £ ² d £ .                                             (16)

о             ^К Ь

Ясно, что c <  1 при J >  0, c >  1 при J <  0 и c = 1 при J = 0. Если материал находится в состояниях упругости и упрочнения, то касательные модули положительны. Следовательно, неравенство J <  0 возможно только после появления в балке зоны разупрочненного материала. Запишем интеграл (16) для значения j = £ ^Z в виде:

К J ( £ ) = J E hp ( £ ) £ ² d £ + J E s ^p ( £ ) £ ² d £ = J 1 + J 2 .

£ ^B

£ ^Z

£ ^B

Здесь    E hp >  0

–

касательный модуль упрочнения   ( E hp = E ,   0 <  £ <  £ T ),

E S <  0 - касательный модуль разупрочнения. Справедливы следующие оценки:

J E^p_h ( £ ) £ 2 d £ < ( £ ) 2 J E h ( £ ) d £ ,

£ ^B

£ ^B

J E S £ ) £ 2 d £ < ( £ ^B ) 2 J E S £ ) d £ .

£ ^Z

£ ^Z

£ ^B

£ ^B

Тогда

^J 1 ^{+ J} 2 < ( ^{£ B} ) ² J E h ( ^£ ) d ^{£ +} J Eh ( ^£ ) d ^£

( £

£ ^Z

A

k ⁰

£ ^B

₂ £ ^Z

= ( £ ^B ) J E^p ( £ ) d £ =

£ ^Z

= ( ^{£ B} ) ² J d £ ^{d £}= ( ^{£ B} ) ² ( ^a ( ^{£ Z} ) ^{- а ( 0 )} ) = ⁰ .

Таким образом, J ( б = £ ^B ) > 0 и J ( 6 = £ ^z ) < 0. Учитывая монотонное возрастание функции | J 2 ( 6 )| при возрастании деформации 6 , находим, что уравнение J ( 6 ) = 0 имеет только один корень, расположенный в интервале ( £ ^B , £ ^z ) . Следовательно, равенство

J = J e^s ( у ) у ² dy = -11 3 J E^p ( £ ) £ ² d £ = 0

0              ^К 0

определяет начало расходимости ряда (14).

Произведем теперь жесткое догружение, увеличив кривизну балки на малую величину К _д . Параметры нового положения равновесия для К = К ₀ + К _д определяются выражениями M = M ₀ + M _д , а = а ₀ + а_д , £ = £ ₀ + £ _д , £ ^p = £ ₀ ^p + £ Д , где а_д , £ _д , £ _д - решение возмущенной исходной задачи с определяющими соотношениями (11) и (12) и граничным условием 6 _д = К _д h . Первым приближением к решению этой задачи являются выражения M ‘= Як _д , £ ‘= К _д у , а ’= Ek у - решение основной задачи (6). Аналогично изложенному выше вычисляем приращения пластических деформаций £ f1 ( у ) и по формулам (10), в которых функцию £ ^р заменяем на функцию £ ^Р _Д1 , получаем решение корректирующей задачи, а именно, M ‘‘ = - M _{Д 1} , а"_Д1 = - E£ hi , e ‘ i = 0. После корректировки имеем M _{д 2} = M'_д + M ‘‘ j , а _д 1 = а ’ + а"_Д1 , £ _д 1 = £‘ . Так как деформации не изменились, то следующая корректировка не нужна, и данные выражения представляют решение возмущенной исходной задачи.

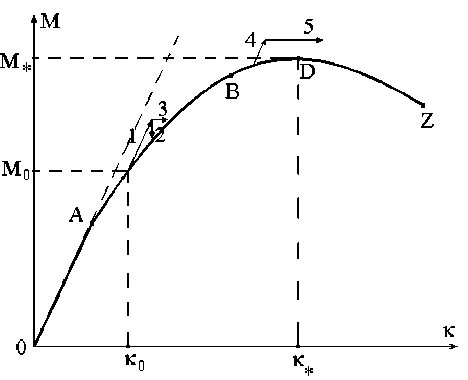
Рис. 3. Диаграмма M ( к ) и схемы итерационных процессов; D ( M * , к * ) - наивысшая точка диаграммы

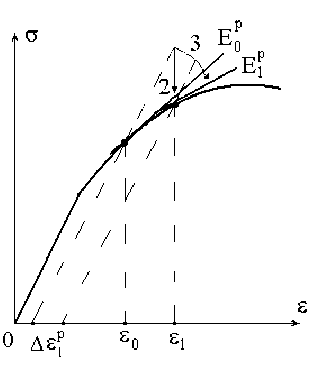
Рис. 4. Схемы итерационных процессов для элемента материала: прямая 2 – жесткое догружение, 3 – мягкое догружение

Если применить данную итерационную процедуру к процессу нагружения, начинающемуся от ненапряженного состояния балки (M0 = 0, к = 0), то можно построить зависимость M (к), качественный вид которой показан на рисунке 3. Точка A отвечает появлению области упрочнения, точка B – появлению области разупрочненного материала, точка Z – зоны разрушения.

Вычисляя производную от функции M (к), находим dM     г до д(кУ) , _Д

— = 2 b 47— ydy = 2 b E p к ) У dy = 2^ы • d к     0 д ( к у ) дк ^J ₀

Следовательно, в наивысшей точке D ( M * , к * ) диаграммы M ( к ) выполняется равенство J = 0. На восходящей ветви имеем J >  0, на ниспадающей - J <  0.

На рисунке 3 также показаны схемы итерационных процессов, построенных выше. Прямые 1 и 2 отвечают жесткому догружению, прямые 1 и 3 – мягкому догружению. Ясно, что процесс при мягком догружении сходится тогда, когда прямая 3 пересекает диаграмму M ( к ) ( J >  0) и расходится, если проходит выше ее наивысшей точки D (например, прямые 4 и 5). В последнем случае кривизна неограниченно растет и, следовательно, балка разрушается. Таким образом, используя итерационную схему вычисления параметров равновесия при монотонном возрастании изгибающего момента, зможно построить только восходящую ветвь кривой M ( к ) .

На рисунке 4 изображены схемы итерационных процессов для элемента материала.

4.    Устойчивость равновесия

Исследуем, наконец, устойчивость положений равновесия балки, опираясь на определение устойчивости по Ляпунову [3].

Определение. Положение равновесия балки при мягком (жестком) нагружении является устойчивым, если для любых /1 > 0 и /2 > 0 можно указать 5 > 0 такое, что при увеличении изгибающего момента на величину Mд < § (кривизны кд < §) следует выполнение неравенств max I£д I < /1, max sf < у2. yy

Пусть при M = M 0 и к = к ₀ балка находится в равновесии и J 0 >  0, то есть M ₀ <  M * ( J ₀ - значение интеграла (17) в данном положении равновесия). Возмутим равновесие мягким догружением (0 <  M _д<  § , § - малая величина). Конечное решение возмущенной задачи существует (ряд (14) сходится), если M _д< § <  M * - M ₀ (все интегралы J k строго положительны). Тогда £_д , £ д ^ 0 при M _д^ 0. Следовательно, условия, сформулированные в определении устойчивости, выполняются и положение равновесия устойчивое.

Если J ₀ = 0, то M = M * . Тогда для любого сколь угодно малого возмущения M _д ряд (14) расходится и £ _д , £ { ^^ . Следовательно, данное положение равновесия неустойчивое.

Когда J ₀ <  0, то координаты ( M 0 , к ₀ ) отвечают точке, находящейся на ниспадающей ветви диаграммы M ( к ) . При любом возмущении ряд (14) расходится, то есть положение равновесия неустойчиво.

Таким образом, условие (17) определяет момент потери устойчивости процесса деформирования балки при монотонном возрастании изгибающего момента.

Возмутим теперь положение равновесия жестким догружением (0 <  к _д<  § ). Решение возмущенной задачи имеет вид:

• £ =     £^р = fl - E 0 ⁽ y ) V

• ^£ д ^{у к} д , ^£ д1 ^{1              £} д .

V E )

Тогда справедливы следующие оценки:

max £ д| = h к_д <  h § ,

max £ 1 = max yy

(

1 —

V

^p E ₀

л

E)

/

^£ д

< ah § ,

где а = max ^y

1 -

^p E ₀

E

. Отсюда для произвольных малых величин у 1 и / 2 всегда найдется

величина § = min ( у1 /h , / 2/ h ) , для которой выполняются условия, сформулированные в определении устойчивости. Таким образом, при жестком нагружении все положения равновесия балки устойчивые.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 07-01-96087).