Итерационная схема решения коэффициентной обратной задачи термоэлектроупругости
Автор: Ватульян Александр Ованесович, Нестеров Сергей Анатольевич
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 4 т.10, 2017 года.
Бесплатный доступ
Представлена общая постановка коэффициентной обратной задачи термоэлектроупругости для неоднородного тела. Обратная задача состоит в определении материальных характеристик материала конечного неоднородного термоэлектроупругого тела как функций координат. Сформулирована слабая постановка в трансформантах Лапласа. Для решения обратной задачи на ее основе применяется метод линеаризации. Получены операторные уравнения, связывающие искомые и измеряемые в эксперименте функции. В качестве примера рассмотрено решение задачи для термоэлектроупругого стержня. При этом соответствующая прямая задача термоэлектроупругости посредством преобразования Лапласа сводится к системе интегральных уравнений Фредгольма 2-го рода, построению решений в виде рациональных функций относительно трансформант и нахождению оригиналов в соответствии с теорией вычетов. Для решения обратной задачи термоэлектроупругости разработан итерационный алгоритм, на каждом шаге которого путем решения интегральных уравнений Фредгольма 1-го рода находятся поправки восстанавливаемых характеристик. Проведено исследование влияния изменения материальных характеристик на дополнительную информацию, необходимую для решения обратной задачи. Выполнены вычислительные эксперименты по восстановлению законов распределения неоднородности в классах степенных и экспоненциальных функций, чаще всего используемых при моделировании функционально-градиентных материалов. Даны рекомендации по выбору наиболее информативных временных диапазонов для съема дополнительной информации. Серия вычислительных экспериментов показала, что погрешность восстановления безразмерных характеристик не превышает 5%.
Термоэлектроупругость, слабая постановка, идентификация, стержень, вычислительный эксперимент
Короткий адрес: https://sciup.org/143163481
IDR: 143163481 | УДК: 534.1 | DOI: 10.7242/1999-6691/2017.10.4.37
Текст научной статьи Итерационная схема решения коэффициентной обратной задачи термоэлектроупругости
В последние годы во многих отраслях промышленности стали широко применяться диагностические приборы и датчики, функционирование которых базируется на явлении пироэффекта, а поведение материала описывается уравнениями термоэлектроупругости.
Уравнения термоэлектроупругости впервые были получены в начале 60-х годов XX века Миндлиным [1, 2]. В настоящее время задачи, рассматривающие колебания однородных и слоистых термоэлектроупругих тел, представлены в литературе достаточно подробно [3–8].
Для совершенствования работы устройств на основе пироэффекта используются новые, в том числе функционально-градиентные пироматериалы (ФГПМ) и учитывается неоднородность поляризации. Под ФГПМ понимаются пьезокомпозиты, обладающие переменными физическими свойствами. Их материальные характеристики являются не константами, а некоторыми функциями пространственных координат; скачки свойств при переходе через поверхность раздела, а также расслоение и растрескивание, присущие слоистым материалам, исключаются.
Решения задач термоэлектроупругости для ФГПМ рассмотрены главным образом для степенных и экспоненциальных законов неоднородности [9–13]. В тоже время актуальным является решение связанной задачи термоэлектроупругости при произвольном распределении неоднородности. Пример такого рода содержится в [14], где анализируется тепловой удар по функционально-градиентному термоэлектроупругому слою. Решение сводится к системе интегральных уравнений Фредгольма 2-го рода в трансформантах Лапласа и последующему применению теории вычетов.
Для правильного расчета характеристик устройств, в которых присутствуют неоднородные пироматериалы, необходимо знание функций, представляющих собой законы распределения неоднородности. Задача идентификации этих функций для термоэлектроупругих тел по некоторой дополнительной информации о граничных физических полях относится к коэффициентным обратным задачам (КОЗ) термоэлектроупругости, которые практически не исследованы, что объясняется сложностью построения операторных соотношений, связывающих заданные и измеряемые в эксперименте функции.
На практике широко распространены два типа постановки обратных задач математической физики. Для первого типа дополнительная информация считается известной во внутренних точках тела в какой-либо момент времени, для второго типа — лишь на части границы и на некотором временном интервале. Чаще всего экспериментально реализуемым является второй тип, несмотря на то, что в этом случае обратная задача нелинейна. В последние годы получил развитие новый подход к решению нелинейных обратных задач механики связанных полей, базирующийся на итерационном процессе, на каждом этапе которого решается соответствующая линейная задача.
С использованием такого подхода успешно проведена идентификация неоднородных характеристик линейных электроупругих [16–19] и термоупругих [20, 21] тел. В [18] для решения КОЗ электроупругости сформулирована слабая постановка и решена задача о реконструкции закона изменения неоднородности модуля податливости стержня при анализе его установившихся продольных колебаний. В [19] предложен способ восстановления свойств неоднородного по толщине электроупругого слоя из анализа плоской задачи об установившихся колебаниях. С помощью преобразования Фурье решены две более простые — несвязанные — краевые задачи относительно усредненных смещения и потенциала. Решение обратной задачи строится на основе метода линеаризации и итерационного процесса, на каждом этапе которого необходимо решать систему интегральных уравнений Фредгольма 1-го рода. В работе приведены примеры одновременного восстановления законов неоднородности пьезомодуля и упругого модуля.
В [20, 21] представлено решение обратной задачи термоупругости применительно к стержню. При этом рассмотрено два способа нагружения — механический и тепловой. В качестве дополнительной информации выступали температура или смещение, измеренные на части границы тела. Для КОЗ термоупругости был построен итерационный процесс, на каждом шаге которого для нахождения поправок восстанавливаемых коэффициентов решались линеаризованные интегральные уравнения Фредгольма 1-го рода.
Цель данной работы состоит в постановке обратной задачи термоэлектроупругости, выводе операторных уравнений для решения поставленной задачи путем итераций, применении полученных уравнений для идентификации неоднородных характеристик термоэлектроупругого стержня из пьезокерамики класса 6 mm, анализе результатов вычислительных экспериментов по восстановлению законов распределения неоднородности для функций различных классов (степенных, экспоненциальных, тригонометрических и логарифмических), как монотонных, так и немонотонных.
-
2. Постановка обратной задачи термоэлектроупругости для неоднородного тела
Уравнения связанной термоэлектроупругости в отсутствие объемных сил, внутренних источников тепла и электрических зарядов имеют вид [14]
CT ij , j = pu ,(1)
Dk,k=0,(2)
-
- qk, k + Ton = 0,(3)
а определяющие соотношения представляются в форме
σij =cijkluk,l-γijθ+ekijϕ,k,(4)
c
-
η = γijui, j + ε θ– giϕ,i ,(5)
T 0
Di = eikluk,l + giθ–эikϕ,k ,(6)
qi =-kijθ.(7)
Здесь: G y — компоненты тензора напряжений; u i — компоненты вектора перемещений; р — плотность; Di — компоненты вектора электрической индукции; qi — компоненты вектора потока тепла; T 0 — температура естественного состояния; п — энтропия; c ijkl — компоненты тензора модулей упругости; Y y — компоненты тензора температурных напряжений; 9 = T - T 0 — приращение температуры T ; ekij — компоненты тензора пьезоэлектрических модулей; ф — электрический потенциал; с Е — удельная объемная теплоемкость при постоянном тензоре деформации; gi — компоненты тензора пирокоэффициентов; эij — компоненты тензора диэлектрических проницаемостей; kij — компоненты тензора теплопроводности. Точка над символом означает однократное дифференцирование по времени, запятая в нижних индексах — дифференцирование по следующей за ней координате.
Рассмотрим движение неоднородного термоэлектроупругого тела V , ограниченного поверхностью S и находящегося под действием механических, тепловых и электрических нагрузок при отсутствии внутренних источников тепла и массовых сил. Поверхность тела может быть представлена в виде: S = Su U S G , S = ST U S q , S = S + U S - U S H где индексами u , g , T ид помечены части границы тела, на которых заданы, соответственно, перемещения, напряжения, температура и тепловой поток. На части границы S - и S + наводится электрический потенциал, граница S H неэлектродирована. Тогда граничные и нулевые начальные условия будут иметь вид:
9ST = 0, q,nj=-kj9^nj\Sq = Q,(8)
ui \ Su = 0 , j \ SG = Pi , ф \ S± = ±фо, Dn\SH = 0,(10)
9( x ,0) = ui ( x ,0) = it, (x ,0) = 0.(11)
Прямая задача термоэлектроупругости заключается в установлении функций u i , 9 , ф из уравнений (1)-(11) при известных характеристиках c ijkl , р , с Е , k j , Y j , ekj , эу , g i ■
В обратной же задаче термоэлектроупругости требуется определить характеристики cijkl , р , с Е , k j , ч у , ekij , эij , gi как функции координат по дополнительной информации, измеренной на доступной для наблюдения части границы S тела. Дополнительной информацией могут служить:
-
- компоненты вектора перемещения d i , измеренные на временном отрезке [ T , T 2 ] на границе S G :
u \ s G = d i ( x , t ), t e [ T , T ] ;
-
- приращение температуры y , измеренное на временном отрезке [ T 3 , T 4 ] на границе Sq :
-
3. Формулировка операторных уравнений для решения обратной задачи термоэлектроупругости
9 \ s q = y ( x , t ), t € [ T 3 , T 4 ] .
Основная проблема исследования обратных задач — это построение операторных соотношений, связывающих искомые и измеряемые в эксперименте функции. Для решения поставленной выше КОЗ запишем слабую постановку прямой задачи термоэлектроупругости в трансформантах Лапласа. Для этого сначала применим к уравнениям (1)–(3) и граничным условиям (8)–(10) преобразование Лапласа по времени с параметром p при начальных условиях (11). В результате получим:
Gij,j = p 2P uti,
D)k, k = 0,(15)
-
- qk, k + pT0n = 0,(16)
9\sT = 0, - kjj 9 ,nj\sq = Q),(17)
u,\su = 0, G jG = pi,(18)
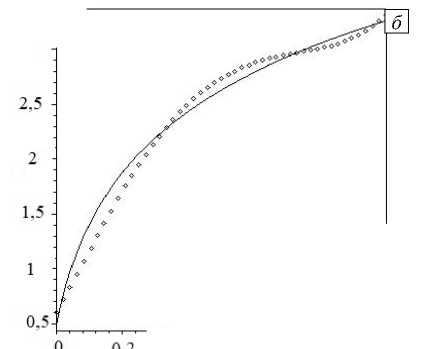
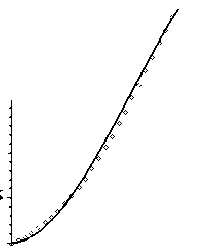
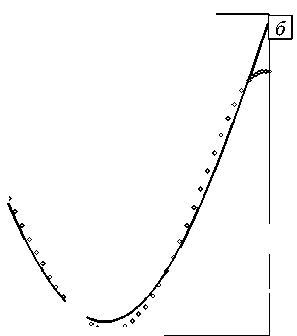
ф \S± = ± Здесь знак «тильда» обозначает трансформанту Лапласа соответствующей функции. Введем в рассмотрение гладкие пробные функции vi, т0 и V, удовлетворяющие главным граничным условиям задачи в трансформантах: vi |S = 0, т0|Sr= 0, V |S = ±ф0. Воспользуемся методом множителей Лагранжа. Умножим уравнение (14) на vi, уравнение (15) — на а1у, уравнение (16) — на а2т0, где аi — неопределенные множители Лагранжа, а затем проинтегрируем их по объему V . Аналогично поступим с граничными условиями: условие на части Sa умножим на а3vi, на части SH — на а4у, на части Sq — на а5т0 и проинтегрируем по соответствующим частям поверхности S. Найдем сумму всех построенных функционалов: J[(aj,j + P2Р Ui) v+а1 Dk, kV +а2 (-PT0n +q i ,i)T0 ] dV + V +а3J (a in - Pi ^dS + а4J DnVdS + а5J (qini - Q)т0dS = 0. (20) S a SH Sq Используя формулу Остроградского–Гаусса и определяющие соотношения, перепишем уравнение (20) в виде: f I 1 2 . ~ ~ ~ ~ Tx — — ~ ~ гх ~ \ ~ I . J ^2p puv-wk,i +yj94,j+ekijф,kvi,j- а1 (eikiuk,i+gi9 - эikф,k )v,i JdV + I 9l~ I «А9, У0,i- a2PT0 I Yyuy + cE — - giPi |T0 dV + к T0 + J ((1 + a3) ajnj - a3P) vidS + (а1 + а4) J Dini VdS + J ((а2 + а5)qini - а5Q )т 0 dS = 0.(21) S a SH Далее, полагая в (21) а1 = 1, а2= -1,(pT0), а3= а4= -1, а5= 1,(pT0), окончательно получим: I 12 1 .''А.1' I JI - р рuv--cijkiU,,jvk,i + ekij (<p,kv Uj + v,kUV1) + -эikp,kV,i IdV + V к2 2 2 II + f 0TO--k,,-9 ,t0, + Yy 16v;,; + т0й,;) - g, Ф, т0 0 ij ,j 0,i ij i,j 0 i,ji i V к 2T0 2pT0у +J TpV),dS —— J Q)тodS = 0 .(22) Sa PT0 Sq Слабым решением задачи (14)-(19) будем называть компоненты физических полей иt, 9, ф, удовлетворяющие интегральному равенству (22) при произвольных гладких функциях vi, т0 и 1ф . Запишем равенство (22) в виде: А (a, й, v) = B(v), (23) I 1т1 1 I г( С- 1 где A(a, и, v) = JI -р рuv, --cijktUi,jvk, 1 + ekij ( + Yj (9V^i,j +т0Utj,j) - gipiт0 IdV — трилинейная форма, то есть форма, линейная по коэффициентам дифференциальных операторов a (cijk1, р, сЕ, kij, Yj, ekij, эу, gi), компонентам трансформант XV); в(V) = -/P-VdS + ^- jeт0dS — Sa PT0 Sq физических полей U (Ui, 9 , ф) и пробным функциям v (vi, т0, линейная форма от трансформант гладких пробных полей vi, т0. Под решением обратной задачи термоэлектроупругости понимается множество элементов (a, U), удовлетворяющих равенству (23) для любых пробных функций v . Легко показать [17], что при двух разных решениях (а(1), и(1)) и (a(2), U(2)) выполняется обобщенное соотношение взаимности или формула Грина: д(л(1) z/2) iI^A-rIu^ ГАА а (a — a , и , и i — в (и — и i. Представленная обратная задача является нелинейной, что вызывало бы существенные затруднения при отыскании ее решения, если бы не трилинейность формы A . Свойство трилинейности позволяет значительно упростить процедуру решения за счет сведения к последовательности слабых постановок и интегральных уравнений первого рода с гладкими ядрами, которые дают возможность реализовать итерационный вычислительный алгоритм, идеология которого описана в [17]. В соответствии с ним сначала из условия минимума функционала невязки выбирается некоторое начальное приближение коэффициентов а(0), например, в классе линейных функций. Пусть и(0) — соответствующее поле, удовлетворяющее слабой постановке А(a(0), й(0), v) — B(v). Применяя линеаризацию в окрестности (a(0), и(0)), вычисляя и(0)|$ — d(0)и используя формулу (24), получим линейное уравнение для нахождения поправок 5a(0): А(5a(0),й(0),u(0)) — B(5 — 5(0)). (25) Затем определим элемент a(1)— a(0)+ 5a(0). Тогда последовательность задач для отыскания (а(n), й(”)) будет формироваться следующим образом: А (a(n), u(n), v) — B (v), а поправки 5a(n) вычислим из линейного операторного уравнения первого рода с компактным оператором: А (5a(n), un), u(n)) — B (d — d(n)). 4. Задача термоэлектроупругости для стержня Покажем конкретное применение предложенного подхода для реконструкции неоднородных характеристик. Рассмотрим одномерную динамическую задачу термоэлектроупругости для неоднородного стержня из пьезокерамики класса 6 mm [14]. Стержень имеет длину l и поляризован вдоль оси x3. Торец стержня x3— 0 жестко защемлен, закорочен и поддерживается при нулевой температуре. На другом торце x3— l действует нестационарная нагрузка, которая может быть тепловой или механической. Тогда начально-краевая задача термоэлектроупругости, в предположении одномерности исследуемого процесса (и, — и2— 0, и3— и(x3, t), 0 — 0(x3, t), ф — ф(x3, t), опишется следующей системой уравнений: (c33и')' + (e33Ф')' -(7330)'— Ри,(27) (e33 и')' — (э 33Ф')' + (g30)' — 0,(28) —70 (Y33 и' — g 3Ф') + (к330')' — c E0 — 0,(29) и (0, t) — 0, ^33( l, t) — p (t),(30) 0(0, t) — 0, — к33( l )0'(l, t) — q (t),(31) ф(0,1) — 0, ф( l, t) — 0,(32) 0( x ,0) — и (x ,0) — и( x ,0) — 0.(33) Символ «штрих» в уравнениях означает дифференцирование по координате x3. Для обезразмеривания задачи (27)-(33) с целью выявления малых параметров введем обозначения: z — -3-, U — - , W 4 • *■ —70 с 33(0) Q1 — q n —к33(0)00 T/— ф — /с33(0) l 0N cЕ(0) , ll 00 q 0 q0 l 1 Ф0 ф0 ^33 (0) _ / с33 (0) _ t1 Vi , Е , 1V Р(0) t2 l t1——, V1 t —сЕ(0) l2 t T — — , t2 Р(z) — ^xl, j(z) — c^aCxa) , к(z) — kзз(-з2 ’ p(0) v ’ c33(0) v ’ к33(0) 2 к33(0) , c к>=,:i(0,), э»(z)— э33 (x3 ) Y (z) — Ь^ Y33(0) , e,3 (z) —e33(x3) g(z) —g 3(x 3) 5 — e33(0) э33(0) , e33(0) , 6 g3(0) ’ 1 cc33(0)э33 (0) 52 —733(0)^ 70 , 53 — g 3(0^ 1 T 70 , n-2ill-12, /.(t) — _В<)к. С 33(0) cЕ(0) э33 (0)сЕ (0) с33(0) c33(0) В результате уравнения (27)-(33) примут вид: д дz s д (_ . xvV) sд 2-д2и + 51 т-1 езз(zН- I-82 — (y(z)W) = е Рту дz V дz ) дz дт д ( д U ^ д ( д V ^ д , §1 Т" I e33 (zН- I -Т" I эзз(z) -т- I+83 — (g(z)W ) = 0, дz V дz ) дz V дz ) дz д(г,.дw) . дw s. д2и s . д2V . —I k(z)— I-c(zН—б2y(z)—+§зg(z= 0, дz V дz ) дт дz дт дz дт и (0, т) = 0, Q(1, т) = Т](т), - aw W (0, т) = 0, - к (1) (1, т) = 0(т), дт V(0, т) = V1(1, т) = 0, аи W (z ,0) = и (z ,0) = — (z ,0) = 0. дт Прямая задача термоэлектроупругости заключается в определении функций U, W, V из решения начально-краевой задачи (34)-(40) при известных характеристиках s (z), р(z), у(z), c (z), к (z), э33 (z), e33 (z), g(z). При произвольных законах изменения коэффициентов дифференциальных операторов осуществить это можно лишь численно. Поступим аналогично работе [14]: применим преобразование Лапласа, аппарат решения интегральных уравнений Фредгольма 2-го рода и обращение трансформант на основе теории вычетов. В обратной задаче термоэлектроупругости для стержня требуется одновременное нахождение характеристик s (z), р(z), у(z), c (z), к (z), э33 (z), e,3(z), g(z) по дополнительной информации о смещении U или температуре W, измеренной на свободном торце стержня z = 1 в некоторых точках временного диапазона: U (1, т) = d (т), те[ a, b ], W(1,т) = Y(т), те[c,d]. 5. Итерационная процедура решения обратной задачи термоэлектроупругости для стержня Слабая постановка задачи (23) позволяет решать обратную задачу идентификации характеристик неоднородного термоэлектроупругого стержня с помощью итерационной процедуры, которой отвечают формулы (26). Первый этап итерационного процесса требует знания начального приближения. Начальное приближение выбиралось из класса положительных ограниченных линейных функций a(0)(z) = C1 z + C2 на основе минимизации функционала невязки на компактном множестве. Из априорной информации о значениях коэффициентов 0 < a - < a0 (z) < a+, где a - и a+— минимальное и максимальное значения коэффициентов соответственно, устанавливались ограничения на искомые константы C1 и C2 в виде системы неравенств a - < C1 < a+, a - < C1 + C2< a+, которые формируют их область изменения в виде компактного множества. После перехода от этой области к сеточной из условия минимума соответствующего функционала на построенном компактном множестве осуществлялся подбор пары (C1, C2). В работе рассмотрено два способа нагружения торца z = 1 термоэлектроупругого стержня — механический (силой Т](т)) и тепловой (тепловым потоком О,(т)). Функционал невязки имел вид: - при механическом нагружении b J< n-1)=J (d (т) - U(n-1)(1, т))2d т; a - при тепловом нагружении d J2 n-1)= J (Y (т) - W(n )(1, т))2d т. с Далее уточнялись законы изменения неоднородных характеристик путем учета поправок 55(n 1), 5р(n 1), Зу(n11, 5c'n11, 5k("11, 8э3(3”11, 5ё("11, 5g'n11, которые находились из условия удовлетворения обезразмеренному операторному уравнению 1-го рода в трансформантах Лапласа, полученному на основе формул (22), (26) применительно к стержню. В развернутом виде операторное уравнение для одновременного нахождения поправок неоднородных свойств термоэлектроупругого стержня выглядело так: 2 1 — о о (n-1) dz + 251 J 5 e3(3n—1) о dU(n1dVx(n1J --1----dz — dz dz 1 1 2J'"'n ' 20 dj^ dz 1 1 2 dz--J5c(n—1) (W(n—1)) dz + 2K 2pToJo 5 k(n—1) / i r\X 2 ( dW(n—1)) , I —;— I dz I dz ) 1 лг7(n11 *, di/(n11 —5 5у(n—i) dU----W(n—i) dz + 5 5 g(n—i) dV1----W< n—i) dz = 2Jn dz 3Jn dz = p (p)(d (p)—и(n—1)(1, p))—- 21 (p)(j (p) — w(n—1)(1, p)). p Ясно, что в общей постановке (34)-(42) задача является недоопределенной, поскольку на практике обычно требуется установить все компоненты тензоров в рамках описанной выше модели, а дополнительной информации (41) или (42) недостаточно для обеспечения единственности решения обратной задачи в рамках одного эксперимента, поскольку операторных уравнений меньше, чем искомых функций. Вопрос о том, возможно ли в принципе обеспечить единственность при нескольких режимах нагружения, не достаточно изучен даже для более простых моделей [22]. Для анализа проблем, которые возникают при решении обратных задач термоэлектроупругости для неоднородных тел, в работе проведено исследование, при котором неизвестной была только одна характеристика, остальные считались известными. В случае восстановления только одной из величин уравнение (45), с учетом конкретного вида нагружения стержня, преобразуется к более простому виду. При идентификации механических — 5 (z), р(z), и электрофизических — э33 (z), ei3(z), характеристик в вычислительных экспериментах использовался механический способ нагружения стержня и дополнительная информация вида (41). При идентификации характеристик теплофизических — c (z), k (z), Y(z), и электрофизической — g(z), имел место тепловой способ нагружения стержня, а дополнительной информации отвечала формула (42). При решении обратной задачи на конечном временном промежутке к операторным уравнениям в трансформантах применялись теоремы операционного исчисления о свертке и дифференцировании оригинала. Операторные уравнения для нахождения поправок в оригиналах выглядели следующим образом: Ядра интегральных уравнений (46)-(53) вычислялись с помощью соотношений: т л//'"1 (nTT).n1 M 1( z’т)= f л (z’т) л (z’т т1) dт1, 0 (V т (V т т. лrrCn-1) лгг(n-1) M 2(z, т) =f Л ( z, т) Л ( z, т т1 ) dт1, * дz дz т д и(n-1) d v(n-1) M 3( z’т)= 1 дz ( z’т) дz ( z’т т1) dт1, гд V(n-1) д V(n-1) M 4( z,т) = | 1 ( z,т) 1 ( z, т т1 ) dт1, 0 дz дz тд W(n-1) M5(z, т) = J (z, т)W( ) (z, т т) dY, 0 дт , тдW(n-1) , ,дW(n-1) , ., M6(z,т)=1 . (z,т) . (z,т т1)dт1, * дz дz , г д W(n-1) , XU U(n-1), M 7( z, т) =1 п ( z, т) ( z, т т1 ) dт1, J0 дт дz тд W(n-1) д V(n-1) M8(z, т)= 1 Л (z, т) 1 (z,1 т1 ) ()dт1 0 дт дz Нахождение поправок из решения интегральных уравнений Фредгольма 1-го рода (46)-(53) является некорректной задачей, которая требует регуляризации. В работе применялся метод регуляризации Тихонова А.Н. с выбором параметра регуляризации по обобщенной невязке [23]. В результате реализации итерационного процесса скорректированные функции имели вид р(n)(z) = р(n-1)(z) + 5р(n-1)(z), Т(n)(z) = Т(n-1)(z) + 5Т(n-1)(z), ev)(z) = ei^-1)(z) + 5e(Г'(z), Э3(3п) (z) = э3(3"-1)(z) + 5э3(3"-1)(z), c(n) (z) = c(n-1)(z) + 5c(n-1)(z), k(n) (z) = k(n-1)(z) + 5k(n-1)(z), Y(n) (z) = Y(n-1)(z) + 5Y(n-1)(z), g(n) (z) = g(n-1)(z) + 5g(n-1)(z) и представляли собой приближенное решение обратной задачи термоэлектроупругости при удовлетворении условиям выхода из итерационного процесса. Условиями выхода служили следующие неравенства: - при механическом нагружениия стержня J(n-1)< 5 • 1 < ио ; - при тепловом с нагружении 6. Результаты вычислительных экспериментов J2n-1)<5о. (55) В расчетах принято, что на свободном торце стержня приложены нагрузки: механическая Т](т) = H(т); тепловая Q1 (т) = H(т). Здесь H(т) — функция Хевисайда. Предельное значение для выхода из итерационного процесса составляло 50= 10-4. При нахождении безразмерных параметров, входящих в уравнения (34)-(40), использовались значения физических постоянных титаната бария (представителя керамики класса 6 mm). Исходя из данных в [14], полагалось, что е = 2 -10-9, 51 = 0,3, 52= 10-2, 53= 2-10-2. При решении обратных задач важно, чтобы изменение восстанавливаемых функций ощутимо отражалось на измеряемой в эксперименте дополнительной информации. Для того чтобы узнать, какие из безразмерных характеристик стержня существеннее всего связаны со снимаемой на свободном торце стержня дополнительной информацией, была проведена серия вычислительных экспериментов. Расчеты показали, что на температуру наиболее сильно влияют теплофизические характеристики — коэффициент теплопроводности k (z) и удельная теплоемкость c (z), а на смещения — упругий модуль Т(z), плотность р(z), пьезомодуль e!3 (z), коэффициент диэлектрической проницаемости э33 (z). В тоже время изменение функций Y(z) и g(z) практически не сказывается на снимаемых на торце экспериментальных данных. Этот факт объясняется малостью безразмерных параметров 52 и 53, входящих в операторные уравнения (52) и (53). Путем анализа дополнительной информации выявлены наиболее значимые с точки зрения идентификации временные интервалы в окрестности начала отсчета. Выяснено, что измерение смещения наиболее информативно на интервале [a, b] = [0,0.6], а измерение температуры — на интервале [c, d] = [0,0.4] при четырех точках наблюдения внутри этих интервалов. С целью более детальной проверки предложенного метода проведены многочисленные эксперименты по восстановлению законов распределения неоднородности, описываемых функциями различных классов (степенными, экспоненциальными, тригонометрическими и логарифмическими), а также как монотонными, так и немонотонными. На рисунках представлены результаты реконструкции характеристик функционально-градиентного материала титаната бария, из которого был изготовлен стержень. На рисунке 1 показаны исходные и восстановленные монотонные функции: коэффициент диэлектрической проницаемости э33(z) = 1,3-0,2z2— функция убывающая, и модуль упругости У(z) = ln(1 +15z) + 0.5 — функция возрастающая. Рисунок 2 содержит графики реконструкции немонотонных функций: удельной теплоемкости — c (z) = -1,6z3 +1,8z2+ 0,5, и коэффициента теплопроводности — k (z) = 2,5 - 0,5 sin(nz). Для сравнения приведены их исходные зависимости от координаты z . Видно, что безразмерные характеристики реконструируются с хорошей точностью: погрешность восстановления функций не превышает 5%. При этом для выполнения условий выхода (54) или (55) требовалось не более 12 итераций. а 3 . 2.5 - 2 - 1.5 - 1 ; 0.5- D 0.2 0.4 0.6 0.8 _ 1 зультат реконструкции коэффициента диэлек сплошной линией, восстановленная – квадра c трической проницаем тиками а 2,4 ■ 2.3 ; 2.2 ■ 2.1 - 2 ■ обезразмеривания и преобразования Лапласа решалась с помощью аппарата интегральных уравнений Фредгольма 2-го рода и нахождении оригиналов решений на основе теории вычетов. Для отыскания поправок восстанавливаемых характеристик в итерационном процессе использовались интегральные уравнения Фредгольма 1-го рода в оригиналах. Проведена серия вычислительных экспериментов по восстановлению характеристик, изменение которых оказывает существенное влияние на дополнительную информацию. Реконструировались законы распределения неоднородности, описываемых функциями из классов степенных, экспоненциальных, тригонометрических и логарифмических функций. Результаты расчетов показали, что дополнительные условия (41) или (42) являются достаточными для однозначного установления одной характеристики при известных остальных и позволяют рассчитать искомую функцию с небольшой погрешностью. Предложенный метод определения неоднородных характеристик термоупругого стержня может оказать большое влияние на совершенствование теоретической базы неразрушающего контроля конструкций из пироматериалов. Работа выполнена при поддержке РФФИ (проект № 16-01-00354-а) и Южного математического института — филиала ВНЦ РАН.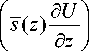
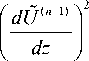
—1J 5р( n—1) M1 (z, т) dz = J Р1(т — Т1)(d (Т1) — U(n—1) (1, Т1)) d Т1, 2 0 0
1J 55-(n—1) M 2 (z, т) dz = J Р1(т — Т1)( d (Т1) — U(n—1) (1, Т1)) d Т1, 2 0 0
(46)
(47)
251J 5ё»—1)Mз (z, т)dz = J Р(т — Т1)(d(Т1) — U(n—1) (1, т))dт , 0 0
(48)
1 1 т
—-J 5.—1) M4 (z, т) dz = J Р (т — Т1)(d (Т1) — U(n—1) (1, Т1)) d Т1,
2 0 0
(49)
1 1 т
- J 5 c(n—1) M 5 (z, т) dz = J 21(т — т1)(Y (т) — W(n—1) (1, т1 ))d т1,
2 0 0
(50)
1 1 т
- J 5k(n—1)M6 (z, т)dz = —J 21 (т — т1)(Y(т) — W(n—1) (1, т1 ))dт ,
2 0 0
(51)
52 J 5Y(n—1) M7 (z, т) dz = J 21 (т — т1 )(Y (т1) — W(n—1) (1, т1)) d т, 0 0
(52)
5з J 5g(n—1) M8 (z, т) dz = —J 21 (т — т1)(Y (т) — W(n—1) (1, т1 ))d т1.
(53)
о о



Список литературы Итерационная схема решения коэффициентной обратной задачи термоэлектроупругости
- Mindlin R. D. On the equations of motion of piezoelectric crystals//Problems of continuum mechanics/Ed. by N.I. Muskilishivili. -Philadelphia: SIAM, 1961. -P. 282-290.
- Mindlin R. D. Equations of high frequency, vibrations of thermopiezoelectric crystal plates//Int. J. Solid. Struct. -1974. -Vol. 10, no 6. -P. 625-637.
- Nowacki W. Some general theorems of thermopiezoelectricity//J. Therm. Stresses. -1978. -Vol. 1, no. 2. -P. 171-182.
- Ватульян А.О, Кирютенко А.Ю., Наседкин А.В. Плоские волны и фундаментальные решения в линейной термоэлектроупругости//ПМТФ. -1996. -Т. 37, № 5. -С.135-142.
- Ватульян А.О. Тепловой удар по термоэлектроупругому слою//Вестник ДГТУ. -2001. -Т. 1(7), № 1. -С.82 -89.
- Bassiouny E., Youssef H.M. Two-temperature generalized thermopiezoelasticity of finite rod subjected to different types of thermal loading//J. Therm. Stresses. -2008. -Vol. 31, no. 3. -P. 233-245.
- Bassiouny E., Youssef H.M. Thermo-elastic properties of thin ceramic layers subjected to thermal loadings//JOT. -2013. -Vol. 1, no. 1. -P. 4-12.
- Shen S., Kuang Z.-B. An active control model of laminated piezothermoelastic plate//Int. J. Solids Struct. -1999. -Vol. 36, no. 13. -P. 1925-1947.
- Wu X.-H., Shen Y.-P., Chen C. An exact solution for functionally graded piezothermoelastic cylindrical shell as sensor or actuators//Mater Lett. -2003. -Vol. 57, no. 22-23. -P. 3532-3542.
- Ying C., Zhefei S. Exact solutions of functionally gradient piezothermoelasic cantilevers and parameter identification//J. Intel. Mat. Syst. Str. -2005. Vol. 16, no. 6. -P. 531-539.
- Zhong Z., Shang E.T. Exact analysis of simply supported functionally graded piezothermoelectric plates//J. Intel. Mat. Syst. Str. -2005. -Vol. 16, no. 7-8. -P. 643-651.
- Ootao Y., Tanigawa Y. The transient piezothermoelastic problem of a thick functionally graded thermopiezoelectric strip due to nonuniform heat supply//Arch. Appl. Mech. -2005. -Vol. 74, no. 7. -P. 449-465.
- Ootao Y., Tanigawa Y. Transient piezothermoelastic analisys for a functionally graded thermopiezoelectrical hollow sphere//Compos. Struct. -2007. -Vol. 81, no. 7. -P. 540-549.
- Ватульян А.О., Нестеров С.А. Динамическая задача термоэлектроупругости для функционально-градиентного слоя//Вычисл. мех. сплош. сред. -2017. -Т. 10, № 2. -С. 117-126.
- Gonzaleza M.G., Sorichettic P.A., Ciocci Brazzanoa L., Santiagoa G.D. Electromechanical characterization of piezoelectric polymer thin films in a broad frequency range//Polym. Test. -2014. -Vol. 37. -P. 163-169.
- Ватульян А.О, Соловьев А.Н. Прямые и обратные задачи для однородных и неоднородных упругих и электроупругих тел. -Ростов-на-Дону: ЮФУ, 2008. -176 с.
- Ватульян А.О. К теории обратных задач в линейной механике деформируемого тела//ПММ. -2010. -Т. 74, № 6. -С. 909-916.
- Ватульян А.О., Дударев В.В. О реконструкции неоднородных свойств пьезоэлектрических тел//Вычисл. мех. сплош. сред. -2012. Т. 5, № 3. -С. 259-264.
- Богачев И.В., Ватульян А.О., Явруян О.В. Идентификация свойств неоднородной электроупругой среды//ПММ. -2012. -Т. 76. № 5. -С. 860-866.
- Ватульян А.О., Нестеров С.А. Об одном способе идентификации термоупругих характеристик для неоднородных тел//ИФЖ. -2014. -Т. 87, № 1. -С. 217-224.
- Nedin R., Nesterov S., Vatulyan A. On an inverse problem for inhomogeneous thermoelastic rod//Int. J. of Solid. Struct. -2014. -Vol. 51(3). -P. 767-773.
- R. Nedin, S. Nesterov, A. Vatulyan. Identification of thermal conductivity coefficient and volumetric heat capacity of functionally graded materials//Int. J. Heat Mass Transfer. -2016. -Vol. 102. -P. 213-218.
- Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. -М.: Наука, 1990. -230 с.


