Итеративный алгоритм восстановления трехмерной формы объекта

Автоматическое измерение формы объектов, геометрии поверхности, уровня кривизны или степени шероховатости - все это очень важно в задачах бесконтактной диагностики, машинного зрения, трехмерного моделирования и стереокопирования.

Известны, например оптико-цифровые устройства для построения стереокопии трехмерных объектов: Hyscan фирмы Hymarc Ltd., Канада; 3Dsystem фирмы Newport Instruments AG, Швейцария. Подобные устройства способны в течение 2-3 секунд построить цифровую копию формы объекта размером около 200x200x200 мм с разрешением 0.05 мм. Компьютеру в этих системах отводится задача обработки структурированного изображения типа интерферограммы, состоящего из набора темных и светлых полос. Известен ряд математических методов, использующихся для восстановления трехмерной формы объектов по их двумерному структурированному изображению: муаровая топография [4]; сдвиговая муаровая топография [5]; Фурье профи-лометрия [6]; фазовая профилометрия [7]. Эти мето- ды во многом совпадают с методами обработки обычных интерферограмм: методом преобразования Фурье [8] и методом выделения центров полос [9].

Основной недостаток этих методов в том, что с увеличением уровня шума в обрабатываемом изображении и при большом числе разрывов полос из-за спекл-эффекта они теряют надежность и могут приводить к большим ошибкам при измерении трехмерной формы объекта. Этот недостаток ограничивает область применения интерферометров и трехмерных сенсоров гладкими поверхностями.

Однако различные методы обработки интерферограмм с ростом шума данных деградируют по-разному. Методы, основанные на анализе пространственного спектра изображения, позволяют эффективно разделять шум и полезный сигнал в частотной плоскости. С другой стороны, ограничение фильтрующим окном спектра изображения ведет к потере части пространственных частот и к уменьшению разрешения функции поверхности.

Компромисс между фильтрацией шума в изображении и сохранением пространственного разре- шения ищут с помощью подходящего выбора формы окна. Например, используют окно Ханнинга [10].

Но выбор формы фильтрующего окна - это полумера. Известно, что увеличить разрешение измерительной системы, восстанавливающей изображение по малому участку пространственного спектра можно с помощью специального итеративного алгоритма Герчберга [11]. Также известно, что оптимальным образом стабилизировать работу системы в присутствии шумов данных можно с помощью универсального метода регуляризации [12].

В связи с этим актуальной является разработка оптимальных итеративных методов, алгоритмов и программного обеспечения для обработки структурированных изображений типа интерферограмм, обеспечивающих устойчивую в присутствии шума данных работу оптико-цифровых систем для автоматического измерения трехмерной формы объекта [13].

Оригинальность данной работы в том, что впервые для задач восстановления формы объекта по его структурированному изображению применены оптимальные итеративные алгоритмы с регуляризацией. Эти алгоритмы позволяют эффективно восстанавливать полную информацию об истинном спектре изображения по его известной части в присутствии шума.

Одно из преимуществ предложенного подхода заключается в том, что разрабатываемое программное обеспечение с минимальной модернизацией применимо для обработки обычных классических интерферограмм в лазерных интерферометрах.

Практическая значимость разработанного метода в том, что он способен существенно ослабить ограничения на уровень шума в оптических системах диагностики поверхности и восстановления формы объектов. Как правило, алгоритмы с регуляризацией позволяют успешно обрабатывать интерферограммы с отношением сигнал/шум равным единице и ниже. При таком уровне шума данных стандартное программное обеспечение для обработки интерферограмм, основанное на выделении центров полос, не работает.

• 2.    Схема наблюдения

Схема получения структурированного изображения показана на рис. 1. На объект проецируются под углом а параллельные световые полосы с синусоидальным распределением амплитуды g ( x’ , y’ ):

g(x',y') = A(1 + cos©x'). (1)

Получаемое в результате распределение амплитуды света на объекте

f (x, У ) = g (x ', У ') = g (x cos a + h (x, y )sin a, y) = , (2) A(1 + cos[to(x cos a + h(x, y) sin a)])

где h(x,y) - функция рельефа в области [xmin,xmax]([ymin,ymax], регистрируется с помощью телекамеры, ось которой перпендикулярна объектной плоскости z=0 (рис. 1.) и получается дискретное изображение f (n ) = 1 +

- exp i ©I ^x m _in

cos a +— n cos a + h ( n ) sin a N

⁺ 1 exP

I    AC^

-i©^xmin cos a +—n cos a + h(n) sin a где A=xmax-xmin, N - число отсчетов в строке изображения.

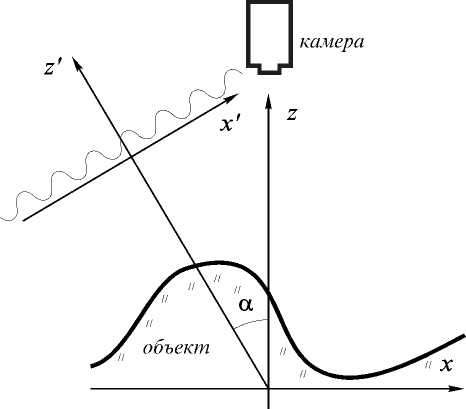
Рис. 1 Оптическая схема наблюдения

Таким образом, задача восстановления рельефа по изображению объекта в структурном освещении с точностью до постоянных коэффициентов совпадает с задачей восстановления распределения фазы по интерферограмме [13]. Действительно, спектр функции f ( n ) представляет собой функцию вида

F(m) = 5(m) + G(m - vA cos a) + G *( m + vA cos a), (4)

где

G ( m ) =

1 e 2 nv x min cos a F L i ^{2 nv} h ( n ) sin a

2                 {

где обозначает дискретное преобразование Фурье.

Тогда функцию поверхности можно рассчитать по формуле:

arg F   {G (m)} + 2n k (n)

h (n) =---------------------------

2n sin a

.

где k ( n ) - функция принимающая целые значения. Она возникает вследствие периодичности фазы.

• 3.    Алгоритм восстановления

Функция

G(m) = F(m + vA cos a) W(m),

полученная методом Фурье-профилометрии, где W ( m ) - функция фильтрующего окна, в качестве которой могут быть использованы, например, функция прямоугольного импульса, или окно Ханнинга, используется в качестве первого приближения для итерационного алгоритма восстановления рельефа. Мы использовали модифицированный итерационный алгоритм Гершберга-Папулиса [11,13].

На к -м шаге в частотной области вычисляется оценка спектра функции рельефа

[S(m), m е D

Gk = i

I Fk(m), m t D

где D - область окна W ( m ),

S ( m ) = I ^{G (} m ) , [ 0,

m е D m t D

фундаментальная составляющая спектра, выделенная в результате применения Фурье-профилометрии, F_k ( m )=7{ f _1 ( n )} - результат применения преобразования Фурье к ( к -1)-й оценке распределения рельефа в объектной области

После применения к ней преобразования Фурье, мы получаем к -е приближение рельефа - комплексную функцию f_k ( n )=7^-1{ G_k ( m )}, фаза которой и представляет собой искомый рельеф.

Далее заменяем ее на функцию с таким же распределением фазы, но с постоянной амплитудой и переходим к следующему шагу итерации.

В присутствии шумов для регуляризации процесса мы используем мультипликативную регуляризацию [13]. В этом случае вместо функции спектра S ( х ) используется функция

7\

S ( 6 ) =

IS(6)12 S(6)

IS(6)12+в-||6| I2,

где в - постоянная регуляризации, или аддитивную регуляризацию, при которой вместо спектра F k ( x ) используется

F _к ( 6 ) = (1 - a ) . [ 1 - D ( 6 ) ] ■ F k ( 6 ) + D ( 6 ) ■ S ( 6 ) ,(11)

где a - постоянная регуляризации,

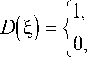
6е D

6t D .

• 4.    Построение модельного изображения

Для исследования работы алгоритма нами было произведено моделирование получения изображения объекта в структурном освещении по заданной функции рельефа h ( х , y ) и параметрам проецирующей решетки - частоте v и углу наклона a .

Для этого в соответствии с (2) для каждого пиксела вычисляется его уровень освещенности. Но поскольку модель (2) не учитывает возможность затенения части изображения, для учета этой возможности предлагается следующая процедура.

Заполнение изображения производится в направлении возрастания х’ вдоль оси х. Для каждой точки (x,y) вычисляется значение x’ по формуле поворота х' = х cos a + h (х, y) sin a (12)

если это значение больше ранее запомненного максимального x’_max , то точка освещена, иначе затенена. Если точка освещена, то ее координата х’ запоминается в качестве нового значения х’^ .

После заполнения изображения по заданному отношению сигнал/шум генерируется шум с нормальным или равномерным распределением.

Таким образом были получены модельные изо-

Рис. 2 Модельные изображения без шума (а) и с шумом (б) отношение сигнал/шум - 1.

• 5.    Численные результаты

В результате обработки изображений на рис. 2 были получены результаты, показанные на рис. 3, соответственно.

а                        б

Рис. 3 Восстановленный рельеф для изображений, приведенных на Рис. 2

Следует отметить, что сдвиг частоты vA cos 9 может оказаться не кратным шагу дискретизации, и тогда возникает наклон восстановленного рельефа по отношению к исходному.

При восстановлении рельефа важной частью алгоритма становится разворачивание фазы для получения рельефа. Мы применяли простую построчную процедуру, которая не справилась с разворачиванием фазы в случае присутствия шумов.

На восстановленных изображениях можно заметить, что затененные участки поднимаются до

“поверхности тени”, то есть область геометрической тени прибавляется к объекту.

• 6.    Литература

  • [1]    Aerospace America, 1990, no. 1, p. 40-41

  • [2]    T. Nouri “Three-dimensional scanner based on fringe projection” Opt. Eng., 1995, v. 34, No. 7, p. 1961-1963

  • [3]    E. M¿ller “Fast three-dimensional form measurement system” Opt. Eng., 1995, v. 34, No. 9, p. 2754-2756

  • [4]    U. Takasaki “Generation of surface contours by moire patterns” Appl. Opt., 1970, v. 9, no. 4, p. 942-947

  • [5]    A. Asundi, K. U. Yung “Phase shifting and logical moire” J. Opt. Soc Am. A, 1991, v. 8, no. 10, p. 1591-1600

  • [6]    M. Takeda, K. Mutoh “Fourier transform profilome-try for the automatic measurement 3D object shapes” Appl. Opt., 1983, v. 22, no. 24, p. 3977-3982.

  • [7]    V. Srinivasan, H.C. Lu, M. Haliona, “Automated phase-measuring profilometry of 3D diffuse object” Appl. Opt., 1984, v. 23, no. 18, p. 3105-3108

  • [8]    Takeda M., H. Ina, S. Kabayashi “Fourier transform method of fringe pattern analysis for Computer-based topography and interferometry” J. Opt. Soc. Am. 1982, v. 72, no. 1, p. 156-160.

  • [9]    T. Yatagai, S. Nakadata, M. Idesawa, H. Saito “Automatic fringe analysis using digital image processing techniques” Opt. Eng., 1982, v. 21, n. 2, p. 432-435.

  • [10]    J. Liu, X. Su “Two-dimensional Fourier transform profilometry for the automatic measurement of three-dimensional object shapes” Opt. Eng. 1995, v. 34, no. 11, p. 3297-3302.

  • [11]    R. W. Gerchberg “Superresolution through error energy reduction. Opt. Acta, 1974, v. 21, p. 709-720.

  • [12]    A. N. Tikonov, V. Y. Arsenin, Solution of Ill-Posed Problems, Winston, Washington DC (1977)

  • [13]    V. V. Kotlyar, P.G. Serafimovich, O.K. Zalyalov “Noise-insensitive iterative method for interferogram processing” Opt. and Laser Technology, 1995, vol. 27, No 4, p. 251-254.

В. В. Котляр, О. К. Залялов

ИТЕРАТИВНЫЙ АЛГОРИТМ ВОССТАНОВЛЕНИџЯ ТРЕХМЕРНОЙ ФОРМЫ ОБЪЕКТА.