Из истории развития концепции математических биллиардов (генезис, динамическое многообразие, приложения)
Автор: Макеев Н.Н.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: История физико-математических наук
Статья в выпуске: 2 (41), 2018 года.
Бесплатный доступ
Рассматривается исторический аспект развития биллиардной модели динамических систем, типы этой модели, а также некоторые ее приложения.
Математический биллиард, теория динамических систем, эргодичность, интегрируемость, история математики
Короткий адрес: https://sciup.org/147245380
IDR: 147245380 | УДК: 514.8; | DOI: 10.17072/1993-0550-2018-2-88-97
Текст научной статьи Из истории развития концепции математических биллиардов (генезис, динамическое многообразие, приложения)
Исторические корни математического биллиарда1

В связи с бильярдной игрой … возникают динамические задачи, решение которых содержится в этом произведении. Люди, знающие теоретическую механику, …, с интересом познакомятся с объяснениями всех оригинальных явлений, которые можно наблюдать во время движения бильярдных шаров.
Гюстав Гаспар де Кориолис. Математическая теория явлений бильярдной игры
Биллиард как настольная игра появился в Европе в XVI в. и вскоре стал популярным видом развлечения. В России он вошел в обиход при Петре Великом, а с 1850 г. распространился по многим городам [1].
Со временем появилось множество видов биллиардной игры, среди которых следует выделить французский биллиард. Он отличается от традиционного биллиарда тем, что биллиардный стол не содержит луз. При этом цель игры состоит в том, чтобы попасть в заданный шар после нескольких столкновений посылаемого шара с другими шарами.
Впоследствии возникает потребность формализованного описания динамики биллиардной игры на основе математического аппарата и законов классической механики. История возникновения этой формализации восходит к трудам Гюстава Гаспара де Кориолиса (1792-1843). В исторических записках упоминается о том, как он часто наблюдал за игрой знаменитого в то время парижского биллиардиста-виртуоза Франсуа Менго. Результаты своих наблюдений Кориолис описал языком уравнений механики и в 1835 г. в Париже издал труд [2], переизданный впоследствии на русском языке [3].
Кориолис в своем труде использовал элементы теории вероятностей, теории пределов, математического анализа. Он первым поставил вопрос о создании математического базиса, описывающего биллиардную игру.
В 1882-1883 годах математическое обоснование теории биллиардной игры было продолжено Анри Резалем (1828-1896) в работах [4-6]. Работа [6] впоследствии была переведена на русский язык [7]. В ней Резаль указал на неточности, содержащиеся в некоторых выводах Кориолиса, приведенных в труде [2], и предложил свое решение, полученное с учетом действия геометрических связей, имеющихся между шарами и биллиардным столом.
Игровой биллиард – прообраз математической модели динамических систем

С развитием теории динамических систем, различных отраслей математики, фи зики, технических наук была установлена общая закономерность, выражающая качественную идентичность определенных черт процессов и явлений, относящихся к описаниям явлений, трактованных данными науками. Это, в свою очередь, вызвало потребность в создании адекватной математической модели, охватывающей данные явления, и удобной для их формализованного описания.
Оказалось, что такого рода удобной моделью может являться схема биллиардной игры , носящей роль прообраза данной модели. Такому наглядному представлению модели способствовало развитие молекулярно-кинетической теории идеальных газов , разработанной Р. Клаузиусом, Дж. Максвеллом, Д. Джоулем и Л. Больцманом. Согласно этой теории динамическое взаимодействие отдельных молекул газа в выделенной системе происходит в виде их упругих соударений подобно соударениям шаров в биллиарде.
Помимо задач теории газов биллиардная схема динамического взаимодействия аппроксимирует и другие задачи классической физики, в частности, задачи оптики, механики идеальной жидкости, акустики [8, с. 93].
Следует также отметить исследования Г. Дарбу (1842-1917) по динамике биллиарда, приведенные в его фундаментальном трактате [9] и опубликованные в русском переводе в 2010 г. [10]. В этой работе получены динамические уравнения движения для общего случая неупругого соударения твердых тел при наличии трения.
К более поздним годам относятся работы ряда авторов: Г. Хемминга (1899) [11], П. Аппеля (1911) [12], Р. Пети (1996) [13]. К этому же направлению исследований относится и монография [14] (1991), в которой к исследованию различных биллиардных задач применены качественные методы. В этой же работе представлены результаты о неинтегри-руемости задачи о традиционном биллиарде.
Возникновение математического биллиарда
Биллиард как математическая модель ( математический биллиард ) впервые была введена Дж. Д. Биркгофом (1884-1944) [15]. Им была поставлена задача, названная впоследствии его именем ( задача Биркгофа ) [16], положившая начало развитию биллиардной модели и расширению представлений о свойствах математического биллиарда [17].
Понятие о математическом биллиарде как о математической модели динамической системы в основе сводится к следующему.
Пусть Q - ограниченная односвязная область с кусочно-гладкой непроницаемой абсолютно твердой границей Γ, расположенная на евклидовой плоскости R2 или на стандартном торе T2.
Классическим математическим биллиардом (далее – просто биллиардом ) называется консервативная динамическая система, порожденная прямолинейным равномерным движением (движением по инерции) материальной точки ( биллиардной точки ) внутри плоской области Q ( биллиардной области ) с ее последующими абсолютно упругими отражениями от твердой границы Γ [8].
Согласно закону упругого отражения угол падения точки равен углу ее отражения. В силу этого величина тангенциальной компоненты скорости точки при ее ударе сохраняется, а нормальная компонента мгновенно изменяет знак. При этом если граница Γ криволинейна, то указанный угол измеряется от касательной к кривой, проведенной в точке удара [18].
Иначе, биллиард - аппроксимирующая модель, представленная движением материальной точки в плоской области Q без трения2 с ее упругими отражениями от твердой неде-формируемой границы Γ или, что тоже самое, отражением лучей света в области Q с зеркальной границей Γ при полном зеркальном отражении (с альбедо a = 1) [18].
Этот закон отражения биллиардной точки применим, в том числе, к областям в многомерном пространстве и, в общем случае, к другим геометриям, а не только к евклидовой. При этом предполагается, что отражение биллиардной точки происходит в гладкой окрестности точки границы Г.
Свойства биллиарда исследовались для различных форм плоской области Q (" биллиардного стола "): эллиптической (в частности, круговой), произвольной овальной, полигональной (в виде многоугольников правильных и произвольных), специальной ("стадион", гриб Бунимовича, торическая фигура) [18] (рис. 1).
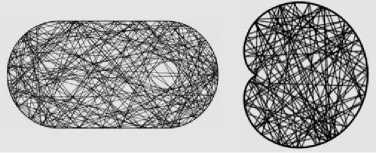
Рис. 1. Стадион и улитка – формы области Q
Биллиарды, как модели, обладают всем комплексом эффектов, характерных для многомерных динамических систем, к которым относятся, в частности, интегрируемость, хаос и ряд других. По характеру и свойствам различают биллиарды классический и динамический. Последний отличается от классического тем, что в нем биллиардная точка движется в заданном поле сил, тогда как в классическом биллиарде эта точка движется по инерции.
Математический биллиард – универсальная модель динамической системы
Динамические системы - обширная область современной математики с развитыми методами исследования и областью приложе- ний. Биллиард является эффективной моделью динамической системы, проявляющей свойства, характерные для ряда разнообразных задач в различных отраслях науки.
Как было отмечено ранее, эта модель впервые была введена Дж. Биркгофом в его исследованиях, выполненных до 1927 г. По результатам этих изысканий им в этом же году была издана монография, которая в русском переводе опубликована в 1941 г. [16]. Это издание в дальнейшем стало библиографической редкостью и в 1999 г. книга Бирк-гофа была переиздана на русском языке [19].
Основополагающая работа [19] в разделе " Некоторые проблемы динамики " (с. 311) содержит следующие биллиардные задачи:
-
• биллиардный шар на эллиптическом столе (с. 319);
-
• частица на гладкой замкнутой выпуклой поверхности (с. 320);
-
• частица на гладкой замкнутой поверхности отрицательной кривизны (с. 321).
После выхода этой фундаментальной монографии динамические системы как новое научное направление стало отдельной интенсивно развивающейся областью математики. Своим трудом Дж. Биркгоф заложил основы общей теории динамических систем.
Свойства биллиардов функционально зависят от свойств его границы, в зависимости от которых устанавливаются их классы. Каждый класс биллиардов обладает своими характерными эргодическими свойствами, существенно отличными от свойств биллиардов других классов.
Динамические системы биллиардного типа (даже при наличии у них различных свойств) по характеру разрывны: в точках отражения биллиардного шара от границы Γ области Q происходит скачкообразное изменение его скорости. При этом свойства неустойчивости движения для разных биллиардных траекторий существенно неодинаковы.
Биллиарды и эргодичность3. Биллиарды представляют собой эффективную модель для исследования свойства эргодичности, изучаемой ранее Л. Больцманом (1844-1906). Эргодическая гипотеза Больцмана утверждает, что фазовый поток, соответствующий движению одинаковых абсолютно упругих шаров в биллиарде с упругими стен- ками (границами биллиардной области) эрго-дичен на связных множествах уровня энергии [20]. Следует уточнить, что эргодичность означает свойство, при котором почти каждая фазовая траектория проводит в каждой измеримой части множества уровня время, пропорциональное мере этой части [21, c. 277].
Исследования Биркгофа, Колмогорова и других авторов показали, что имеют место системы, для которых определяющую роль в их поведении играет лишь интеграл энергии. Такие системы и являются эргодическими.
Биллиарды и энтропия. Биллиардные задачи содержались в исследованиях А.Н. Колмогорова (1903-1987). В своих записях от 22 сентября 1958 г. он определил темы работ, которые планировались им распределить между своими учениками [8, с. 94].
Возможность математически строгого подхода к биллиардным задачам появилась после публикации в 1958 г. работы Колмогорова [22]. В этой работе он ввел в эргодическую теорию фундаментальные понятия энтропии данной системы и понятие К-сис-темы (динамической системы с "хорошими" статистическими свойствами) [8].
Рассмотрим отдельные виды биллиардов, классифицируемых в зависимости от их структурных свойств.
Рассеивающие биллиарды. Во второй половине XX в. появилась эргодическая теория рассеивающих (или гиперболических ) биллиардов ( Я.Г. Синай [20]). К ним относятся биллиарды, у которых граница составлена из конечного числа C3-гладких компонентов, строго вогнутых внутрь области Q. В таких биллиардах имеет место гиперболический характер движения биллиардной точки, а показатели Ляпунова - ненулевые, почти всюду в фазовом пространстве [8, с. 93]. Для такого рода биллиардов граница Γ, взятая в качестве зеркала, рассеивает (делает расходящимся) узкий пучок параллельных лучей света, падающий на нее из области Q. Такие биллиардные системы теряют свойства гладкости (и даже непрерывности) в некоторых точках фазового пространства.
Примером такой системы является сферическая молекула, движущаяся на торе или на квадрате, при упругих отражениях от других закрепленных сферических молекул. В.И. Арнольду (1937-2010) принадлежит наглядное представление аналогии между данными биллиардами и геодезическими потоками в про- странствах отрицательной кривизны. Рассеивающую функцию отрицательной кривизны в такого рода системах выполняет край (граница Г) биллиардной области Q, выпуклый внутрь нее.
Арнольд рассматривает задачу о движении биллиардной точки по торическому биллиарду с круглой стенкой, находящейся в середине данной области, от которой биллиардная точка упруго отражается. Движение на этом биллиарде можно рассматривать как определенный случай геодезического потока на гладкой поверхности. Эту поверхность можно образовать гипотетически, рассматривая тор с отверстием как двустороннюю поверхность, которой следует придать определенную толщину, сгладив ее острое ребро. В результате образуется поверхность с топологией сферы, имеющей две ручки. При "раздувании" этого тора с отверстием возникает поверхность отрицательной кривизны. Таким образом, движение в торическом биллиарде можно представить как предельный случай движения биллиардной точки по геодезическим на поверхности отрицательной кривизны [21, с. 278].
В 1970 г. появилась работа Я.Г. Синая [20] (рис. 2), ставшая основополагающей в исследованиях свойств биллиардов [8, с. 95]. Она содержала первое доказательство основной теоремы, относящейся к рассеивающим биллиардам. В этой работе рассматриваются динамические системы, порожденные движением биллиардной точки в областях со строго выпуклым внутрь краем - в таких, что оператор
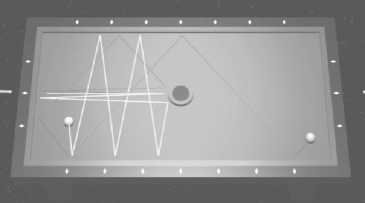
Рис. 2. Пример биллиарда Синая второй квадратичной формы в каждой точке границы области отрицательно определенный, если считать ее край оснащенным полем внутренних нормалей. Было установлено, что такие динамические системы эргодичны.
Синаем было установлено, что для рассеивающего биллиарда имеет место экспоненциальная неустойчивость биллиардных траекторий: движение биллиардного шара с течением времени приобретает хаотический характер. Этим было строго опровергнуто принятое ранее утверждение о существовании признаков хаотического движения механических систем лишь при наличии у них большого числа степеней свободы [8].
Данный вид биллиардов является дискретным аналогом гладких гиперболических систем, определенным в пространстве R n.
Интегрируемые биллиарды. Как известно, системы уравнений динамики разде- обладает полным квадратичным интегралом (рис. 5).

Рис. 5. Траектории эллиптического биллиарда
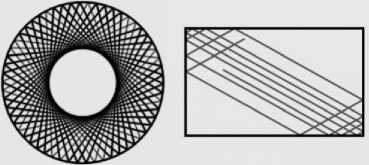
Рис. 3. Траектории движения шара в интегрируемом биллиарде ляются на интегрируемые и неинтегрируемые. Интегрируемые динамические системы обладают достаточным числом независимых первых интегралов. Например, согласно классической теореме Бура–Лиувилля, для интегрируемости гамильтоновой системы с n степенями свободы в квадратурах достаточно знать n первых интегралов, попарно находящихся в инволюции [21, c. 235]. В силу этого можно выделить интегрируемые биллиардные системы, обладающие полным набором независимых интегралов. На рис. 3 изображен пример траекторий в интегрируемом биллиарде, а на рис. 4 – его аналог.

Рис. 4. Картина Эшера – аналог интегрируемого биллиарда
Одним из простейших интегрируемых биллиардов является биллиард Понселе [23]. Согласно теореме Ж.В. Понселе (1788-1867), если биллиардная точка движется в области с эллиптической границей, а ее прямолинейная траектория касается другого эллипса, то эта траектория замкнута, а сам биллиард априори
В 2010 г. вышла книга [23], посвященная классической теореме Понселе, обобщениям и применениям положений концепции математических биллиардов. В ней рассматриваются задачи об интегрируемых биллиардах в области, находящейся на стыке проективной, алгебраической геометрий, теории эллиптических функций и гиперэллиптических кривых. Приведено описание множества интегрируемых биллиардов, в том числе и многомерных.
Здесь же во взаимосвязи с динамикой математических биллиардов приводятся различные конструкции дифференциальной геометрии, относящиеся к исследованиям Кейли, Понселе, Дарбу. Представлены новые интегрируемые возмущения биллиардов.
Авторами указаны взаимосвязи между интегрируемыми биллиардами и задачами из других областей физики и математики - с квантовым уравнением Янга-Бакстера, моделью Гейзенберга, а также геометрией пучков квадрик и гиперэллиптических якобианов. В частности, приводится описание решения проблемы аналитического представления траекторий периодических биллиардов в квадриках. Рассмотрены поризмы Понселе, теорема Понселе и примеры интегрируемых биллиардов [15, c. 449-450].
Существует и другое определение интегрируемости биллиарда. Биллиард называется интегрируемым по Биркгофу , если для него имеется n – 1 полиномиальных по скорости интегралов, находящихся попарно в инволюции и почти всюду независимых [19].
Как было отмечено, традиционный биллиард не является интегрируемым [14]. Интегрируемые биллиардные системы - редкое исключение среди всего возможного множества биллиардов вследствие сложного характера поведения фазовых траекторий типичных биллиардов. В общем случае эти траектории не умещаются на поверхности уровня интегралов, независимых от интеграла энергии.
Можно привести ряд примеров интегрируемых биллиардных систем: геодезические потоки на гладких поверхностях вращения; геодезический поток на трехосном эллипсоиде; биллиард внутри эллипса; система трех точечных вихрей двумерной гидродинамики идеальной жидкости; биллиарды в аффинных камерах Вейля. В частности, было показано, что интеграл биллиарда с границей Γ является интегралом геодезического потока на Γ. Справедливо и обратное утверждение.
В последнее время были найдены новые примеры интегрируемых биллиардных систем: гармонический осциллятор, находящийся внутри эллипса; биллиарды на поверхностях постоянной кривизны. Много новых примеров было открыто путем применения метода обратной задачи теории рассеяния [24].
Биллиард Биркгофа. Образцом типичного (по [14]) биллиарда является биллиард Биркгофа, для которого сформулирована задача Биркгофа о выпуклом биллиарде. Для этого биллиарда граница Γ - замкнутая выпуклая кривая, заданная на евклидовой плоскости R2 . Биркгоф доказал [19], что у гладкого выпуклого биллиарда существуют периодические траектории любой наперед заданной длины, а также хаотические движения.
Биркгофу принадлежит интерпретация биллиарда как диффеоморфизма кольца на себя. Он рассматривал биллиарды как предел задачи о геодезических кривых выпуклой поверхности, непрерывно деформирующейся в плоскую область.
Впоследствии было построено трехмерное обобщение биллиарда Биркгофа, которое выглядит следующим образом. Пусть Q – заданная односвязная область трехмерного пространства и гладкая поверхность Γ – ее граница, являющаяся изнутри зеркальной. Траектория луча света внутри области Q подчиняется закону идеально зеркального отражения. Полученная таким образом динамическая система и является указанным обобщением.
Аналогичным образом можно определить обобщенные биллиарды и более высокой размерности как в евклидовом, так и в неевклидовых пространствах.
Биллиарды и статистические законы. Появление биллиардных моделей создало новые предпосылки к пересмотру исторически старой фундаментальной проблемы - возникновению статистических законов для консервативных динамических систем, следующих из законов классической динамики. Дж. Лейбовиц, О. Пенроуз, Дж. Форд освещали результаты исследований по биллиардным системам, получившим впоследствии известность среди физиков и биологов [8].
В работах П.С. Лапласа (1749-1827) была выдвинута гипотеза о том, что динамические системы классической механики не обладают статистическими свойствами. Эта гипотеза была основана на положении о том, что движения таких систем однозначно определены в силу априорного характера задания начальных условий [20]. Однако для всякой динамической системы реальное значение имеет движение ячейки фазового пространства, в которой точки перемещаются согласно заданным уравнениям движения. Законы движения таких ячеек могут иметь характер, отличный от характера движения их отдельных точек [8].
Примечательно, что даже в простых консервативных системах ячейки фазового пространства, имевшие первоначально правильную форму, впоследствии деформируются и размещаются сложным образом. Это явление может рассматриваться как свойство необратимости динамических систем классической механики. Идея о такой необратимости была впервые предложена Н.С. Крыловым (1917-1947) в 40-х годах прошлого века [25].
Отмечается, что необратимость подобного рода имеет место даже у систем с небольшим числом степеней свободы, а не только у многостепенных систем, как считалось ранее [20].
Характер движения отдельной ячейки фазового пространства, соответствующей динамической системе, связан со свойством устойчивости, а деформация самой ячейки обусловлена неустойчивостью. В силу необратимости и соответствующие статистические свойства системы связаны также с неустойчивостью движения. Это характерное явление отмечалось в 1963 г. М. Борном (1882-1970) [26], а также в книге Крылова [25]. Однако, как утверждается в статье [27], подход Крылова приемлем на физическом уровне логической строгости, но он не вполне убедителен с точки зрения математики.
Двойственные биллиарды. В конце 1950-х годов Дж. фон Нейманом (1903 -1957) в концепцию математического биллиарда бы- ло введено понятие двойственного (или внешнего) биллиарда. Впоследствии этот вид биллиарда стал популяризовать Юрген Курт Мозер (1928-1999).
Существование периодических траекторий для двойственного биллиарда в многоугольной биллиардной области было доказано в 2007 г. С.Л. Табачниковым в работе [28]. Эта работа содержит изложение доказательства, ранее полученного К. Калтером. Другая задача для данного биллиарда содержит доказательство полиномиальности [29]. Помимо этого было доказано, что двойственное биллиардное отображение является симплектическим [18, c. 163].
Построена наглядная интерпретационная модель двойственной биллиардной системы как механической системы - одномерного импульсного осциллятора. Эта механическая система изоморфна двойственному биллиарду относительно некоторой заданной замкнутой выпуклой кривой, параметризованной характерным углом. Этот угол образован касательной к данной кривой в ее текущей точке [18, 30]. Данная интерпретация сходна с известной моделью, построенной на аналогии между движением точки по заданной окружности и движением ее проекции на фиксированную прямую, расположенную вне окружности.
Было установлено, что орбиты двойственного биллиарда относительно полукруга уходят в бесконечность [31].
В 2009 г. вышла книга Р. Шварца [32], посвященная подробному анализу двойственного биллиарда относительно четырехугольников, диагональ которых является осью симметрии. Для таких биллиардов также имеют место орбиты, уходящие в бесконечность, однако характер их ухода гораздо сложнее, чем для полукруга.
Статья Шварца [33] содержит анализ двойственного биллиарда относительно окта-гональной биллиардной области. Полученные им результаты по характеру свойств аналогичны результатам, найденным ранее для пен-тагональной области Табачниковым [18].
Биллиарды внутри квадратичных поверхностей. Серия работ, опубликованных В. Драговичем и М. Раднович за 1998-2006 гг., посвящена биллиардам внутри квадратичных поверхностей и геодезическим на этих поверхностях [34-37]. Содержание данных работ отражено в книге [23].
Эти авторы получили условия, при которых биллиардные траектории замкнуты. Ранее такие условия в случаях выполнения теоремы Понселе были найдены А. Кэли (1821 -1895). Результаты исследований по этой же теме представлены в работах Б. Хесина и Табачникова [18, 38, 39].
В работе [40] (2010) обсуждается полная интегрируемость биллиардной системы на контактных многообразиях. При этом в статье [38] предлагается вариант теоремы Понселе для светоподобных геодезических на эллипсоиде, находящемся в пространстве Г. Минковского (1864-1909).
Хаотические биллиарды. В классическом биллиарде движение биллиардной точки подчинено законам геометрической оптики. Однако в композитных оптических средах лучи света, проходя через внутренние границы раздела оптически разнородных сред, на их границах отражаются и преломляются [41]. Эти особенности порождают механизмы ха-отизации в биллиардных системах, названных композитными биллиардами [42].
В таких системах при расщеплении лучей света на границе раздела оптических сред с разными показателями преломления возникает неоднозначность в образовании направлений биллиардных траекторий. В результате проявляются детерминированные периодические, квазипериодические или хаотические законы движения световых лучей.

Рис. 6
Таких хаотических законов движения существует континуум . При этом траектории биллиардов хаотически переходят с одного листа многолистного фазового пространства на другой его лист. Такая хаотичность изначально заложена в любом биллиарде с расщеплением лучей [42]. На рис. 6 изображены траектории хаотического квантового биллиарда в областях – стадион и улитка Паскаля.
Примером такого рода хаотического биллиарда является асимметричный кольцевой биллиард, образованный двумя эксцентрическими кругами (границами Γ1, Γ2 круго- вой биллиардной области Q) с разными показателями преломления световых лучей (внешним и внутренним). При этом один из кругов находится целиком внутри другого.
В работе [41] рассмотрена динамика световых лучей в таком композитном ( хаотическом ) биллиарде. Эта биллиардная схема является асимметричным обобщением плоской схемы симметричного кольцевого биллиарда с концентрическими стенками-круга-ми, рассмотренными в статье [42].
Обобщенные биллиарды. Биллиардная модель, непрерывно развиваясь, принимает более абстрактные формы, соответствующие возникающим более общим задачам математики и смежных с ней наук. Обобщаются основные понятия и базовые элементы биллиардной модели. Так, было введено понятие обобщенной биллиардной области [43].
Простейшей элементарной (или составной элементарной ) плоской областью Q называется двумерное связное компактное плоское гладкое риманово многообразие с кусочно-гладким краем, имеющее (или не имеющее) изометричное вложение в плоскость.
На основе этого определения получен ряд оригинальных результатов изысканий.
В настоящее время интенсивно проводятся исследования свойств биллиардов с медленно изменяющимися параметрами. Рассматривается динамика в медленно вращающихся прямоугольном и эллиптическом биллиардах с медленно изменяющимися границами. Эти системы близки к интегрируемым и для их исследования могут применяться методы теории возмущений. В данных системах имеют место резонансные явления - захват в резонанс и рассеяние на резонансе. При исследовании этих явлений используются методы, разработанные в теории гладких гамильтоновых систем с быстрыми и медленными переменными.
Применение обобщенных биллиардов в динамике твердого тела. В 2015 г. вышла статья [44], посвященная обобщенному биллиарду, движение при котором происходит на локально плоской поверхности. В ней показано, что известные интегрируемые случаи системы уравнений динамики твердого тела и гиростата в задаче о движении вокруг неподвижного полюса, а также при движении в неограниченной идеальной жидкости, при определенном выборе значений их параметров моделируются обобщенными локально плоскими интегрируемыми биллиардами. Это относится к соответствующим уровням интегралов.
В работе отмечены случаи интегрируемости, являющиеся по Лиувиллю эквивалентными обобщенным биллиардам с областями, ограниченными дугами софокусных квадрик. Этими случаями являются случаи Эйлера, Лагранжа, Ковалевской, Жуковского, Горячева-Чаплыгина - для классического твердого тела и случаи Сретенского, Ковалевской-Яхьи, Клебша и Соколова - для гиростата и для твердого тела, движущегося в жидкости.
Другим примером применения биллиардной модели к динамическим задачам твердого тела является задача о динамике связки двух тел, движущейся на орбите [45].
Заключение
В настоящее время концепция математических биллиардов является неотъемлемой частью бурно и динамично развивающихся областей математического знания и, в частности, теории динамических систем, возможности развития которой непрерывно расширяются. Ее развитие обусловлено естественным общим развитием многих современных разделов математических и смежных с ними наук.
Методы исследования свойств математических биллиардов, с одной стороны, примыкают к классической геометрии, а с другой - находятся на стыке отраслей современной математики и механики: теории чисел, топологии, эргодической теории и теоретической механики. Это - многократно апробированная эффективная модель для исследования эргодичности и эффекта перемешивания в гамильтоновых системах. Вместе с тем, исследование свойств биллиардных систем актуально как для самой математики, так и для смежных с ней отраслей знания и их приложений.
Настоящий обзор представляет в кратком виде ретроспективный взгляд на отдельные моменты исторического развития концепции математических биллиардов и не претендует на полноту изложения ввиду обширности данной темы.
Список литературы Из истории развития концепции математических биллиардов (генезис, динамическое многообразие, приложения)
- Брокгауз Ф.А., Ефрон И.А. (издатели). Энциклопедический словарь. В 86 т. СПб.: Семеновская Типолитография 1890-1907. Т. III A (6). 1892. С. 864-865
- Coriolis G. Theorie mathematique des effets du jeu de billiard. Paris, 1835.
- Кориолис Г. Математическая теория явлений биллиардной игры. М.: Гостехиздат, 1956. 235 с.
- Resal H. Sur un point de la theorie mathematique des effets du jeu de billard // Comptes Rendus Hebdomadaires des Seances de rAcademie des Sciences. 1882. T. 94. P. 1548-1551.
- Resal H. Du choc de deux billes posees sur un tapis de billard // Comptes Rendus Heb-domadaires des Seances de rAcademie des Sciences. 1882. T. 95. P. 655-659.
- Resal H. Commentaire a la theorie mathema-tique du jeu de billard // Journal des mathe-matiques pures et appliques. 1883. T.9. P. 65-98.
- Резаль А. Комментарии к математической теории явлений биллиардной игры // ИВУЗ. Прикладная нелинейная динамика. 2010. Т. 6, № 2. С. 415-438.
- Мухин Р.Р. Из истории гамильтонова хаоса: биллиарды // ИВУЗ. Прикладная нелинейная динамика. 2008. Т. 16, № 6. С. 86-98.
- Darboux G. Cours de mecanique. Paris, 1884. T. 2. P. 547-581.
- Дарбу Г. Геометрическое исследование ударов и столкновений тел // ИВУЗ. Прикладная нелинейная динамика. 2010. Т. 6, № 2. С. 387-413.
- Hemming G.W. Billiards mathematically treated / ed. McMillan, Londres, Grande-Bretange. 1899. 45 p.
- Appell P. Sur le mouvement dune bille de billard avec frottement de roulement // Journal des mathematiques pures et appliques. Ser. 6. 1911. T. 7. P. 85-96.
- Petit R. Billiard: theorie du jeu / ed. Chiron. Paris, 1996.
- Козлов В.В., Трещев Д.В. Биллиарды. Генетическое введение в динамику систем с ударами. М.: Изд-во МГУ, 1991.
- Обзор. Проблемы теории удара. Биллиарды // ИВУЗ. Прикладная нелинейная динамика. 2010. Т. 6, № 2. С. 371-372.
- Биркгоф Дж. Д. Динамические системы. М.; Л.: Гостехиздат, 1941. 406 с.
- Болотин С.В. Интегрируемые биллиарды Биркгофа // Вестник Московского ун-та. Сер. 1: Математика. Механика. 1990. № 2. С. 33-36.
- Табачников С.Л. Геометрия и биллиарды. М.; Ижевск: НИЦ Ин-т компьютерных исследований, 2011. 182 с.
- Биркгоф Дж. Д. Динамические системы. Ижевск: Издательский дом "Удмурдский ун-т", 1999. 408 с.
- Синай Я.Г. Динамические системы с упругими отражениями. Эргодические свойства рассеивающих бильярдов // Успехи математических наук. 1970. Т. 25, вып. 2 (152). С. 141-192.
- Арнольд В.И. Математические методы классической механики. М.: Наука, 1974. 432 с.
- Колмогоров А.Н. Новый метрический инвариант транзитивных динамических систем и автоморфизмов пространств Лебега // Доклады Академии наук СССР. 1958. Т. 119, № 5. С. 861-864.
- Драгович В., Раднович М. Интегрируемые биллиарды, квадрики и многомерные поризмы Понселе. М.; Ижевск: НИЦ Ин-т компьютерных исследований. 2010. 338 с.
- Теория солитонов. Метод обратной задачи: сб. статей. М.: Наука, 1980. 319 с.
- Крылов Н.С. Работы по обоснованию статистической физики. М.: Изд-во Академии наук СССР, 1950. 208 с.
- Борн М. Физика в жизни моего поколения. М.: Изд-во иностранной лит., 1963. 536 с.
- Синай Я.Г. К обоснованию эргодической гипотезы для одной динамической системы статистической механики // Доклады Академии наук СССР. 1963. Т. 153, № 6. С. 1261-1264.
- Tabachnikov S. A proof of Cultefs theorem on the existence of periodic orbits in polygonal outer billiards // Geometry Dedicata. 2007. Vol. 129. P. 83-87.
- Tabachnikov S. Complexity of piecewise convex transformations in two dimensions, with applications to polygonal billiards // Moscow Mathematical Journal. 2006. Vol. 6. P. 673-701.
- Табачников С. Внешние биллиарды // Успехи математических наук. 1993. Т. 48, вып. 6 (294).
- Dolgopyat D., Fayad B. Unbounded orbits for semicircular outer billiard // Annals Henri Poincare. 2009. Vol. 10. P. 357-375.
- Schwartz R. Outer billiards on kites. Annals of Mathematics Studies / Princeton University Press. Princeton, 2009.
- Schwartz R. Outer billiards, arithmetic graphs, and the octagon. Preprint arxiv: 1006. 2782.
- Dragovic V., Radnovic M. Conditions of Cayley's type for ellipsoidal billiard // Journal Mathematical and Physical. 1998. Vol. 39. P. 355-362.
- Dragovic V., Radnovic M. On periodical trajectories of the billiard systems within an ellipsoid in Rd and generalized Cayley's condition // Journal Mathematical. 1998. Vol. 39. P. 5866-5869.
- Dragovic V., Radnovic M. Cayleytype conditions for billiards within k quadrics in Rd // Journal Physical. 2004. Vol. 37. P. 1269-1276.
- Dragovic V., Radnovic M. Geometry of integrable billiards and pencils of quadrics // Journal Mathematical Pures and Appliques. 2006. Vol. 85. № 9. P. 758-790.
- Genin D., Khesin B., Tabachnikov S. Geodes-ics on an ellipsoid in Minkowski space // Enseign. Mathematical. 2007. Vol. 53. P. 307- 331.
- Khesin B., Tabachnikov S. Pseudo-Rieman-nian geodesicsand billiards // Adv. Mathematical. 2009. Vol. 221. P. 1364-1396.
- Khesin B., Tabachnikov S. Contact complete integrability // Regular Chaotic Dynamics. 2010. № 15. P. 504-520.
- Яновский В.В. и др. Хаотические режимы асимметричного кольцевого биллиарда с отражением и преломлением лучей // ИВУЗ. Прикладная нелинейная динамика. 2007. Т. 15, № 1. С. 42-60.
- Барьяхтар В.Г. и др. Хаос в композитных биллиардах // ЖЭТФ. 2006. Т. 130, № 2(8). С. 335.
- Фокичева В.В. Топологическая классификация интегрируемых биллиардов: дис.. канд. физ.-мат. наук. Москва, МГУ. 2016.
- Фокичева В.В., Фоменко А.Т. Интегрируемые биллиарды моделируют важные интегрируемые случаи динамики твердого тела // Доклады Академии наук. 2015. Т.465,№ 2. С. 150-153.
- Белецкий В.В., Панкова Д.В. Связка двух тел на орбите как динамический биллиард: препринт // Ин-т прикладной математики им. М.В. Келдыша РАН. 1995. № 7. 32 с.


