Из опыта преподавания. XIV. О разнообразии тетраэдров
Автор: Войтеховский Ю.Л.
Журнал: Вестник геонаук @vestnik-geo
Рубрика: Научные статьи
Статья в выпуске: 4 (352), 2024 года.
Бесплатный доступ
В статье предложен вывод 25 комбинаторно-геометрических видов тетраэдров, относящихся к 8 точечным группам симметрии. Среди них 3 простые формы: кубический (-43m), тетрагональный (-42m) и ромбический (222) тетраэдры - и 5 комбинаций: тригональная пирамида и моноэдр (3m), 2 планальных диэдра (mm2, 2 вида), 2 аксиальных диэдра (2, 3 вида), планальный диэдр и 2 моноэдра (m, 5 видов), 4 моноэдра (1, 11 видов). Показано, что невозможны тетраэдры с симметрией 23, -4 и 3 - подгруппами точечной группы симметрии кубического тетраэдра. Пример рекомендован к рассмотрению в курсе кристаллографии по теме «Простые формы и их комбинации».
Тетраэдр, комбинаторно-геометрический вид, простая форма, комбинация простых форм, точечная группа симметрии
Короткий адрес: https://sciup.org/149145388
IDR: 149145388 | УДК: 548.12 | DOI: 10.19110/geov.2024.4.4
Текст научной статьи Из опыта преподавания. XIV. О разнообразии тетраэдров
Подоплека этой статьи такова. Как-то после лекции о простых формах и их комбинациях к нам подошел студент-геолог и заявил: вы-де сказали, что есть только три тетраэдра (кубический, тетрагональный и ромбический), а я вот нарисовал четвертый, и, кажется, возможны другие. В конспекте лекций был изображен тетраэдр с разными гранями (длины ребер были помечены разными штрихами). Пришлось предложить студенту обдумать определение простой формы еще раз и пообещать вернуться к вопросу о разнообразии тетраэдров в начале следующей лекции. Тема действительно обойдена в учебниках кристаллографии (Попов, Шафрановский, 1964; Чупрунов и др., 2004). Справедливости ради — при изложении теории простых форм и комбинаций она с необходимостью не возникает. Но отдадим должное любопытному студенту за неожиданный вопрос.
Как выпуклый многогранник (комбинаторно) тетраэдр уникален. Из его имени строго выводимо, что все 4 грани — треугольники, сходящиеся по 3 в каждой из 4 вершин. Но метрическое разнообразие тетраэдров бесконечно. Форму каждого можно зафиксировать
(с точностью до энантиоморфизма) величинами трех ребер, исходящих из одной вершины, и углов между ними. Длины ребер положительны, непрерывны, не-ограничены и независимы. Углы положительны, непрерывны, ограничены (< 180°) и зависимы в сумме (<360°). Итак, форма тетраэдра задана координатной точкой в 6-мерном континууме, равномощном 1-мерному (Кантор, 1985). А все же натуральных чисел (счетной бесконечности) не хватит, чтобы их пронумеровать.
Перечисление
Перечисление тетраэдров по точечным группам симметрии (т. г. с.) интересно уже тем, что позволяет построить их систему в промежутке между «одним» и «бесконечно многим». Здесь видна философская подоплека кристаллографии, на которую тоже следует обращать внимание студентов. Но сосредоточимся на вопросе. Алгоритм перечисления состоит в следующем. Всякая т. г. с. подразумевает автоморфизмы, отображающие однородные элементы тетраэдра друг в друга, при этом грани могут быть 3 типов: равносто-
ронние, равнобедренные и разносторонние. Их набор кодируется тремя числами. Так, кубический тетраэдр получает код [400], тетрагональный — [040], ромбический — [004]. Всего можно составить 15 таких (комбинаторных) кодов: [400], [ 310] , [ 301] , [220], [ 211] , [ 202] , [130], [121], [112], [103], [040], [031], [022], [013], [004]. Четыре из них (зачеркнуты) противоречивы: 3 равносторонние грани требуют такой же четвертой — получаем тетраэдр [400]; 2 равносторонние требуют две равнобедренные — получаем тетраэдр [220].
Перебор остальных вариантов удобно вести в порядке «убывания»: с равносторонними гранями, потом без них, но с равнобедренными, наконец, только с разносторонними. Восстановим ли тетраэдр по коду? Не всегда: [400] — заведомо кубический, но [040] — не обязательно тетрагональный. В одном типе следует различать (совместимо или зеркально) равные и разные грани. Так, в форме [0.2 + 2.0] есть 2 пары равнобедренных граней, в [0.2 + 1 + 1.0] — пара и 2 уникальные. Всего таких (комбинаторно-геометрических) символов можно составить 51. На рис. 1 даны только геометрически реализуемые варианты. Ребра равной (разной) длины отмечены одинаковыми (разными) буквами.
Характеристика
Тетраэдры охарактеризованы комбинаторно-геометрическими кодами и т. г. с. в таблице 1. Их взаимно-однозначное соответствие имеет место лишь для самых симметричных форм: кубического, тетрагонального, ромбического тетраэдров и комбинации тригональной пирамиды с моноэдром. Для них коды могут служить именами. В других случаях код характеризует тетраэдр точнее, чем т. г. с. Лишь для кода [0.2 + 2.0] возможны два тетраэдра с т. г. с. mm2 (№ 16) и 2 (№ 11) (выделены в табл.). Итого тетраэдров с т. г. с. mm2 — 2, т. г. с. 2 — 3, т. г. с. m — 5, т. г. с. 1 — 11. При этом 8 т. г. с. относятся к 6 из 7 (без гексагональной) сингониям с ростом числа форм к низкосимметричным: кубической, тетрагональной и тригональной — по 1, ромбической — 3, моноклинной — 8, триклинной — 11 (табл. 1).
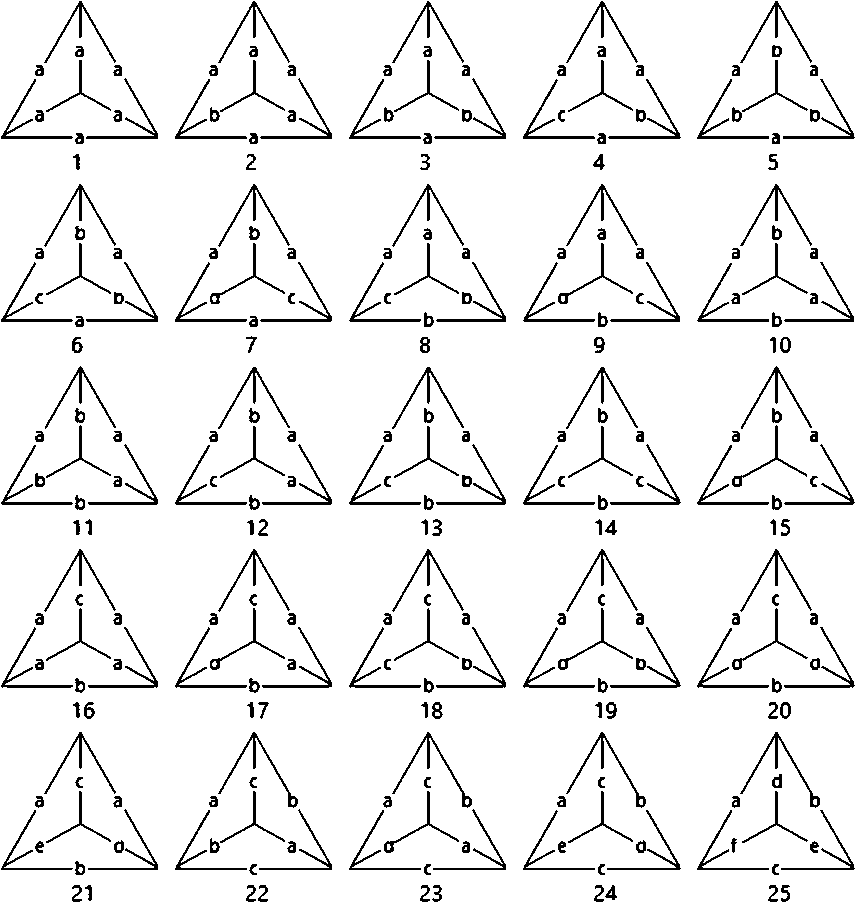
Рис. 1. Комбинаторно-геометрические типы тетраэдров. Пояснения в тексте
Fig. 1. Combinatorial-geometric types of tetrahedrons. See text

Таблица 1. Характеристики тетраэдров
Table 1. Characteristics of tetrahedrons
|
№ на рис. 1 и код No. in Fig.1 and index |
Т. г. с. PSG |
Интерпретация Interpretation |
Сингония Syngony |
|
1 [400] |
-43m |
кубический тетраэдр cubic tetrahedron |
кубическая cubic |
|
10 [040] |
-42m |
тетрагональный тетраэдр tetragonal tetrahedron |
тетрагональная tetragonal |
|
5 [130] |
3m |
тригональная пирамида + моноэдр trigonal pyramid + monohedron |
тригональная trigonal |
|
22 [004] |
222 |
ромбический тетраэдр rhombic tetrahedron |
ромбическая |
|
2 [220]; 16 [0,2+2,0] |
mm2 |
2 планальных диэдра 2 planal dihedrals |
rhombic |
|
11 [0,2+2,0] ; 12 [022]; 23 [0,0,2+2] |
2 |
2 аксиальных диэдра 2 axial dihedrals |
моноклинная |
|
3 [1,2+1,0]; 6 [112]; 8 [0,2+1+1,0]; 14, 20 [0,1+1,2] |
m |
планальный диэдр + 2 моноэдра planal dihedron + 2 monohedra |
monoclinic |
|
4 [1,1+1,1]; 7 [1,0,1+1+1]; 9, 13, 18 [0,1+1+1,1]; 15, 21 [0,1,1+1+1]; 17, 19 [0,1+1,1+1]; 24, 25 [0,0,1+1+1+1] |
1 |
4 моноэдра 4 monohedra |
триклинная triclinic |
Исключения
Нетрудно заметить, что все т. г. с. в таблице — это подгруппы т. г. с. -43m кубического тетраэдра (Вайнштейн, 1979). Но почему среди них нет т. г. с. 3 , 23 и -4 (рис. 2)? Понять это несложно. В случае т. г. с. 3
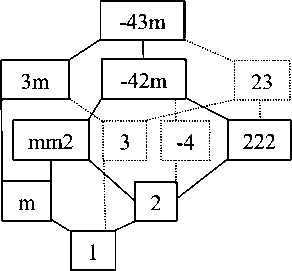
Рис. 2. Подгруппы точечной группы симметрии -43m . Пояснения в тексте
Fig. 2. Subgroups of the symmetry point group -43m. See text ось симметрии L3 тетраэдра должна проходить через вершину и центр противоположной грани. Но тогда она равносторонняя, а боковые грани равнобедренные — получаем тетраэдр [130] (3m). В случае т. г. с. 23 (3L24L3) повторим рассуждение для 4L3 и получим тетраэдр [400] (-43m). В случае т. г. с. -4 инверсионная ось Li4 проходит через середины двух ребер, которые отождествляет. Она же уравнивает 4 других ребра — получаем тетраэдр [040] (-42m).
По сути, построить тетраэдры с т. г. с. 3 , 23 и -4 не позволяет малое число граней, к тому же все треугольные. Ранее на многообразиях выпуклых 4-…12-эдров и простых 13-…16-эдров показано, что при большем числе граней разные соединения даже одного набора могут давать огромное число комбинаторно различных полиэдрических форм (Войтеховский, Степенщиков, 2008).
Заключение
Рассмотренная задача о тетраэдрах хороша уже тем, что на простом примере показывает студентам стиль решения перечислительных задач, приведших к фундаментальным константам: 14 решеток О. Браве (ранее их нашел М. Франкенгейм, но — увы — 15, а не 14), 32 т. г. с. — А. В. Гадолина (ранее их нашел И. Гессель, но результат был надолго забыт), 47 простых форм и 230 пространственных групп симметрии Е. С. Федорова — А. Шенфлиса (оба поначалу ошиблись на 2—3 группы, но указали друг другу на это в переписке) и многие другие в высших разделах кристаллографии (многомерной и цветной). Одним словом, на этом примере всякий студент может проверить, годится ли он для работы в этой области.

Рис. 3. Рождественская поздравительная открытка из архива Д. П. Григорьева: «Die Kristallographie im “ Hortus Sanctus ” des Jacob Meydenbach zu Mainz 1491». («Кристаллография в “Священном саду” Якоба Мейденбаха, Майнц, 1491». — Пер. Ю. В .)
Fig. 3. X-mas greeting card from the archive of D. P. Grigoriev: «Crystallography in Jacob Meidenbach's « Hortus Sanctus » in Mainz in 1491»
Казалось бы, что может быть проще тетраэдра? Но напомним, что именно на нем О. Браве увидел инверсионную ось симметрии ( Li4 ), о которой до того геометры не знали более 2000 лет. В кристаллографии и кристаллохимии тетраэдр — незаменимая фигура. Задолго до их становления тетраэдр можно видеть в первых средневековых энциклопедиях по естественным наукам (рис. 3). А он все продолжает ставить перед нами вопросы. Представляется, что вывод комбинаторно-геометрических видов тетраэдров поможет студентам прочно усвоить концепцию простых форм и их комбинаций.
Автор благодарит рецензента за тщательное рассмотрение рукописи и весьма квалифицированные замечания.
Список литературы Из опыта преподавания. XIV. О разнообразии тетраэдров
- Вайнштейн Б. К. Современная кристаллография. Т. 1. Симметрия кристаллов, методы структурной кристаллографии. М.: Наука, 1979. 384 с.
- Войтеховский Ю. Л., Степенщиков Д. Г. Комбинаторная кристалломорфология. Кн. IV. Выпуклые полиэдры. Т. 1. 4-…12-эдры; т. 2. Простые 13-…16-эдры. Апатиты: КНЦ РАН, 2008. Т. 1 - 833 с., т. 2 - 828 с.
- Кантор Г. Труды по теории множеств. М.: Наука, 1985. 430 с.
- Попов Г. М., Шафрановский И. И. Кристаллография. М.: Высшая школа, 1964. 370 с.
- Чупрунов Е. В., Хохлов А. Ф., Фаддеев М. А. Основы кристаллографии. М.: Физматлит, 2004. 500 с. EDN: QJMJFN


