Изменение формы вертикально стоящего упругого резервуара с жидкостью

В процессе исследования покоящейся жидкости в вертикально стоящих упругих резервуарах, часто возникает вопрос о форме, которую принимает резервуар. Например, как изменяется форма заправленной топливом ракеты на стартовом столе, какова роль гидростатического давления в изменении формы грудного отдела аорты человека и т. д.

Решение этой задачи в классическом труде [1] основывается на т. н. «мембранной теории». В этой теории рассматриваются силы и моменты сил в элементе оболочки вертикально стоящего резервуара, заполненного покоящейся жидкостью. Составляется дифференциальное уравнение 4-го порядка для радиальной деформации резервуара. Несмотря на достаточно большую сложность и громоздкость преобразований, результат частного решения дифференциального уравнения оказывается достаточно тривиальным: относительная деформация площади сечения резервуара на определенном уровне пропорциональна гидростатическому давлению на этом уровне. В дальнейшем будет показано, что этот результат слишком грубый для правильной оценки формы резервуара.

Используется также другой подход, основанный на т. н. «безмоментной теории» [2]. В этой теории используется уравнение Лапласа, которое позво- ляет приближенно оценить напряженное состояние в стенках резервуара под действием внутреннего давления.

Достаточно разнообразно данная задача исследуется в биомеханике, например [3–5]. Задача исследуется с разной степенью сложности, но основное внимание часто уделяется биомеханическим особенностям стенок аорты и других кровеносных сосудов.

Целью настоящей работы является исследование способа нахождения формы вертикально расположенного упругого цилиндрического резервуара, заполненного покоящейся жидкостью, определение условий, необходимых для достижения корректного результата решения поставленной задачи.

1. Уравнение Бернулли для упругого трубопровода

Рассмотрим модельную задачу нахождения формы открытого вертикального цилиндрического резервуара с упругими стенками и жестким дном, рис. 1, в который налита жидкость (вода).

Пусть в сечении 1, у дна резервуара координата h = h i , а гидростатическое давление Р_г / _с = P 1 _г / _с . На поверхности жидкости в сечении 2 находится начало координат h = 0, где давление Р_г / _с = 0. Используем давление, избыточное над атмосфер

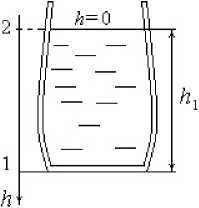
Рис. 1. Изменение формы упругого резервуара

Fig. 1. Changing the shape of an elastic reservoir

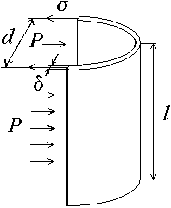
Рис. 2. Участок оболочки вертикального упругого резервуара

Fig. 2. Section of the shell of a vertical elastic tank

ным. Так как жидкость находится в состоянии покоя, то ее вязкость роли не играет.

На дне резервуара гидростатическое давление равно

P 1 г / с = Р gh 1 - ⁽¹⁾ где g = 9,8 м/с² - ускорение свободного падения, р - плотность жидкости.

Распределение гидростатического давления по

ции упругой стенки трубопровода Р и его площади сечения S , поэтому знаки дифференциалов разные. Эта форма записи закона Гука фактически получена в [1] на основе «мембранной теории» при решении уравнения для радиальной деформации

высоте резервуара имеет вид

^Pг / с = ^р gh ,

тонкостенного упругого резервуара, если принять D = E 5 / d [8], где 5 - толщина стенки резервуара, d – его диаметр, Е – модуль упругости материала оболочки резервуара.

Принято также, что вихрей в потоке не образу-

ется, течение потенциальное [9], т. е. rot V = 0, где

Распределение гидростатического давления по высоте упругого резервуара, согласно формуле (2), носит линейный характер. Оно, очевидно, не должно зависеть от того, жесткие у резервуара

5 W

V - вектор скорости, следовательно, =

d V

Преобразуем уравнение (4), считая жидкость не-

сжимаемой, т. е. р = const:

стенки или упругие.

Для учета упругости стенок резервуара найдем уравнение Бернулли в упругом трубопроводе с движущейся в нем жидкостью.

В [4; 6; 7] рекомендуется для волнового процесса в упругом трубопроводе использовать уравнение

8 V д р V ²   р W ²

р — +--+---

8 1   8 X   2     2

V

о Л

Р 2

+ P --= 0.

2 D

Если течение жидкости стационарное, т. е. a v

— = 0, то уравнение (6) можно проинтегрировать:

импульса в виде

dt    дX    dr    р SdX где V и W – продольная и поперечная составля-

р V ² + р W ²

P ²

+ P -   = const.

2 D

ющие скорости жидкости, r – радиальная коор-

дината, Х – продольная координата, t – время,

S – поперечное сечение тонкостенного упругого трубопровода. Вязкость жидкости не учитываем.

Преобразуем уравнение (3) к виду

8 V    8 V    8 W р +p V +p W = at     ax     dx

-

d ( PS )

S 8 X "

8P  „ 8S    dP„ 8 P

=---P----=---+ P, dx   s ax   axd

При записи (4) использован закон Гука для упругого трубопровода в виде [3]:

Проанализируем более подробно причину возникновения последнего слагаемого в (7). Покажем, что оно является следствием закона Гука в форме (5), который для удобства преобразований запишем в виде P - P _o = D A S / S , где P _o - начало отсчета давления.

Исследуем более детально связь между упругостью стенок резервуара D и модулем упругости вещества стенок Е , а также геометрическими размерами резервуара. Разрежем мысленно вдоль небольшой участок резервуара длиной l и средним диаметром d , рис. 2.

Сила давления, избыточного над P _o, растягивающая резервуар, равна силе сопротивления его стенок:

d P = - D — , S

( P - P ₀) ld = 2 ( о-о ₀ ) 5 1 ,

где D – упругость стенки трубопровода. Формула (5) характеризует связь распределенной реак-

где ст - механические напряжения в стенке резервуара толщиной 5 , CT 0 - механические напряжения в стенке резервуара при давлении P ₀ .

Следовательно, давление в резервуаре равно Р—Ро = 2(g —G0)5/d. Полученное соотношение носит название формулы Лапласа. Однако формула Лапласа принципиально неточная. Термодинамический анализ показывает, что более точная формула lnP = ( 0[10]. Разлагая экспоненту в ряд, получаем

2 ( g —g₀ ) 5 1

P — р = р -3---- 0J_ + _ р

^{0   0}     D d     2 ⁰

f 2 ( g-G o ) 5 J ²

Dd

.

Из первого слагаемого в правой части как первого приближения (формула Лапласа) следует P o = D .

Учитывая закон Гука g — G 0 = Е е = Е A d / d , где s = A L / L = A ( п d ) / ( п d ) = A d / d — относительная деформация длины окружности L стенки резервуара ( L = п d ), A d - изменение диаметра резервуара при его растяжении, получаем:

„ „   2 E A d 5    1 ( 2 E A d 5|

P — P =+

0     d ²    2 D ( d ^{2 J}

.

Найдем связь между относительным изменением площади сечения резервуара A S / S и относительной деформацией его диаметра A d / d . Учитывая связь между площадью сечения и диаметром резервуара S = п d ²/4, находим производную dS A S п d                     A S    A d

®—- = —, следовательно, — = 2 —.

d ( d ) A d    2 ^, д               ’ S d

Поэтому для давления, избыточного над Р о , получаем:

„ „   E 5 A S   1 Г E 5 A S ) ²

P — P l =---+----

⁰ d S 2 D ( d S J

„ A S  1 L A S ) 2

= D --+ D ,

S   2 DI   S J или

^P — ^P 0

—

( ^P — ^P0 ) ² _ _D&S .

2 DS

Полученный результат при P ₀ = 0 показывает, что если применить закон Гука в виде (5), то более правильно вместо давления Р использовать вели-

P ²

чину P — —, как это принято в формуле (7). Данный вывод не связан с течением жидкости.

В случае если на текущую по упругому трубопроводу жидкость действует гравитационная сила, в левую часть уравнения (7) необходимо добавить объемную плотность потенциальной энергии жидкости в гравитационном поле. В этом случае уравнение (7) приобретет вид

_ P ²     ,  р V ² р W ²

P — +Р gh +    +     = const,

2 D   22

где h – высота рассматриваемого элемента жидкости над уровнем отсчета.

P ²

Величина P_c = — представляет собой объемную плотность энергии растянутой упругой стенки. Величину Р_с можно отождествить с некоторым давлением.

Полагая статическое давление:

P_C m = P — P_C ,                                         (9)

получаем стандартную форму уравнения Бернулли. Будем использовать термин «давление» для величины Р , учитывая, что оно не тождественно измеряемому статическому давлению.

Таким образом, уравнение Бернулли для упругого трубопровода ничем не отличается от такового для жесткого трубопровода. Так же как и в жестком трубопроводе, сумма статического P_cm , гидростатического P ,,/ _C = р gh и динамического P дu _^ =Р V ² / 2 + Р ^ ² / 2 давлений в каждом поперечном сечении упругого трубопровода остается постоянной.

Однако в уравнение Бернулли (8) входит не статическое давление P , а давление P = P + P , ñò                    ñò ñ которое равно сумме статического давления и некоторого давления, которое равно объемной плотности энергии растянутой упругой стенки. Отметим, что в жестком трубопроводе при D ^ » давление P = Pcm.

Найдем распределение всех давлений по высоте упругого резервуара.

P ²

Используя формулы (2) и (9), с учетом P_C = — получим:

P ²

р gh = ^{P —} 2 D"                                  ⁽¹⁰⁾

В отличие от уравнения (8), координата h направлена сверху вниз, рис. 1.

Решая квадратное уравнение (10) относительно давления Р , найдем:

P = D — V D ² — 2 D р gh .                           (11)

Знак плюс перед корнем неприемлем, т. к. при D ^» (жесткие стенки резервуара) величина Р должна стремиться к гидростатическому давлению Р ^ р gh .

Давление, определяемое объемной плотностью энергии растянутой упругой стенки резервуара, найдем по формуле (9):

P c = P — р gh = D — V D ² — 2 D р gh — р gh .            (12)

На рис. 3 показано распределение давлений по высоте резервуара с упругими стенками. Для расчета приняты следующие параметры: плотность

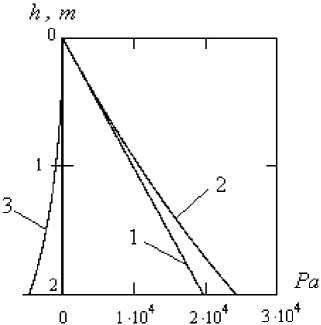
Рис. 3. Распределение давлений по высоте вертикального резервуара с упругими стенками: прямая 1 – гидростатическое давление P , / _с ; 2 - давление P = P ,/ _с + P_c ; 3 - объемная плотность энергии растянутой упругой стенки резервуара – P_ñ Fig. 3. Pressure distribution along the height of a vertical tank with elastic walls: straight line 1 - hydrostatic pressure P , / _c ; 2 - pressure P = P ,/ _c + P_c ; 3 - volumetric energy density of the stretched elastic tank wall – P_ñ

Применим закон Гука в виде, аналогичном [2], где подобная запись используется при анализе относительного удлинения стержня:

A( dS)

AP = - D     , dS

где A ( dS ) - изменение дифференциала площади сечения резервуара. Знак минус определяется тем же, что и в случае формулы (5), A P - это реакция упругой стенки резервуара на жидкость.

Учитывая зависимость площади сечения резервуара от высоты S = f ( h ) , перейдем от приращений к дифференциалам:

« dh dP = - D—dh---=

= - D

dS d2S 2

2 dh       d ² S dh ²

dh ----= - D--Ц---dh .

dS         dS dh

жидкости (воды) p = 1000 кг/м³, упругость стенки резервуара (для наглядности, как у резины) D = 64000 Н / м². Эта величина зависит от диаметра резервуара, толщины его стенки, модуля Юнга вещества стенки D = E 5 / d [8].

Все давления равны нулю на поверхности жидкости в упругом резервуаре и достигают максимального значения на дне резервуара.

Найдем форму стенки вертикального упругого резервуара, в который налита вода. Пусть высота жидкости в резервуаре H , а площадь жесткого дна резервуара S_H .

Заметим, что точность формул (10), (11) и (12) определяется справедливостью использованного закона Гука в виде (5).

2. Нахождение формы вертикального резервуара с упругими стенками

Применение закона Гука для упругой стенки резервуара в виде (5) при решении поставленной задачи невозможно, т. к. эта формула слишком грубо описывает зависимость давления и площади поперечного сечения резервуара. Действительно, если рассматривать формулу (5) как дифференциальное уравнение первого порядка, то в результате интегрирования возникает только одна постоянная интегрирования. Поэтому невозможно удовлетворить сразу двум граничным условиям: площадь поверхности жидкости в области жесткого верхнего обруча S = S q и площадь жесткого дна упругого резервуара S = Sh .

Преобразуем формулу (14):

dP dh

-

_n d 1 I dS ■ D — ln I —

dh

dS

dh

.

Уравнение (15) можно один раз проинтегрировать:

P

D

. 1 I dS

- In     I

C 1 ( dh

где C ₁ - постоянная интегрирования.

Следовательно:

dS I P1 = C. exp - dh   1 4 D)

Используем связь между давлением Р и высотой h в виде (10). Нужно отметить, что формула (10) найдена из более простой формы закона Гука (5). Поэтому на данном этапе в проводимый анализ вносится некоторое приближение. Это прибли-

жение связано с тем, что решение уравнения импульса (3) совместно с законом Гука (13) в аналитическом виде затруднительно. Изменением высоты жидкости при изменении формы резервуара пренебрегаем, что предполагает небольшую деформацию формы резервуара.

Дифференцируя (10), имеем:

dh 1 Г P 1

=      1 -     .

dP p g D

Умножив (17) на (18), получим:

dS dP

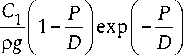
Интегрируя (19), находим:

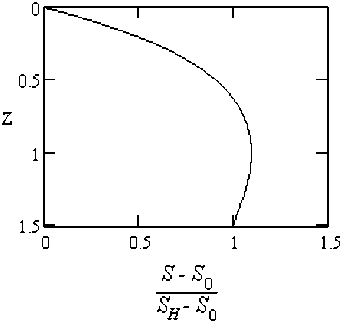
Рис. 4. Зависимость относительной площади поперечного сечения резервуара от безразмерной высоты жидкости в нем Z = p gh ID

Fig. 4. Dependence of the relative cross-sectional area of the tank on the dimensionless height of the liquid in it Z = p gh ID

резервуара будет максимальной. Находя производную от (23) и приравнивая ее к нулю, имеем, что при давлении P m = D площадь сечения резервуара S_m будет максимальной. Из формулы (23) находим:

S m

SH

-

S ₀

-

S ₀

P

= m e exp P_H

-

-

PH

P m

CI

S = 1Pexpl -1+

PgI

где C 2 - вторая постоянная интегрирования.

Если площадь поверхности жидкости в упругом резервуаре задана за счет жесткого обруча S = S о , то, учитывая давление на поверхности жидкости P = 0, найдем C 2 = S о . Следовательно, формулу (20) можно записать в виде

C    I P

S - S = — P exp--

⁰ P g   Ч D

Кроме того, учитывая площадь жесткого дна резервуара S = S ^ , найдем:

C I P I

Sh - S 0 =p 1 exp l-- D H I Ph ,                      (22)

Формула (24) фактически характеризует изгиб-ные свойства стенок упругого вертикального резервуара и позволяет найти в расчете связь величин площадей S_m , S ₀ и S_H .

Приближенно, при достаточно жесткой стенке резервуара, т. е. при достаточно большой величине D , на данном заключительном этапе анализа, чтобы не увеличивать громоздкость формул, примем самую простую зависимость P = f ( h ) , а именно P ²

(10) при условии P » P c = —. Считаем, что давление Р пропорционально высоте жидкости h , отсчитанной от поверхности ко дну резервуара, P ® p gh . Фактически мы приравняли давление Р к гидростатическому давлению Р_г । _с .

Для расчетного примера положим, что Ph I P m = = HI h m = 3 1 2, где h m - положение максимальной площади S_m поперечного сечения упругого резервуара. Таким образом, мы приняли, что максимальная площадь поперечного сечения упругого резервуара возникает на высоте 1 / 3 от его дна.

Следовательно:

S m

SH

-

S ₀

-

S ₀

P

= P m exp P_H

-

1 -

PH

Pm

« 1,1.

где Рн - давление Р на дне резервуара.

Поделив (22) на (21), получим:

^{S - S} o     ^P

----= — exp ^SH - ^S 0 P H

P

-

-

D

PH D

В технике часто возникает задача определения деформации высокого вертикально стоящего резервуара с периодическими или непериодическими подкреплениями оболочки горизонтальными круговыми внутренними обручами с заданной площадью S 0 i . Формула (23) позволяет оценить изменение формы оболочки на каждом участке такого резервуара. В этом случае постоянные C _{1 i} и C _{2 i} будут изменяться от участка к участку. Эти постоянные определяются по формуле (20) последовательно, начиная с верхнего участка, в соответствии с давлениями на верхней и нижней границах участков.

Проведем анализ полученной зависимости (23). Найдем, при каком давлении Р площадь сечения

Учитывая, что для данного случая Ph = -Pm = 3 ²

= —D = p gH, найдем связь высоты жидкости в ре-

2                                       3D зервуаре и упругости его стенок H = -—.

При практических расчетах порядок анализа обычно иной. По заданным параметрам: высоте

жидкости в резервуаре Н и упругости его стенок D – находится положение h_m максимальной площади сечения резервуара. Кроме того, в практических расчетах предположение P ® p gh вряд ли допустимо. По-видимому, для зависимости P = f ( h ) допустимо использовать также приближенную формулу (11), однако это делает выкладки значительно более громоздкими.

Учитывая P m = D и Ph I P m =p gH ID = 312, записываем формулу (25) в виде

^S - ^S 0

^SH - ^S 0

2 P

3 P

--exp-- 3 D I 2 D

.

На рис. 4 показан график зависимости относительной площади сечения упругого резервуара от

величины Z = PID ® p gh ID , построенный по формуле (26).

Заключение

На основе простейшей формы закона Гука, связывающей давление в упругом трубопроводе, по которому течет жидкость, и относительную деформацию площади поперечного сечения упругого трубопровода, найдено уравнение Бернулли для этого трубопровода. В это уравнение входит объемная плотность энергии растянутой упругой стенки, которую можно отождествить с некоторым давлением.

Показано, что используемый вид закона Гука не позволяет найти форму модельного вертикально стоящего упругого резервуара с жестким дном и жестким верхним обручем, заполненного жидкостью.

Переход к более точной записи закона Гука позволил найти форму такого упругого резервуара. Проведен анализ этой формы. Найдено давление, на уровне которого возникает максимальное увеличение площади упругого резервуара.