Измерение диэлектрических коэффициентов полярных жидкостей на СВЧ с применением универсальных номограмм

Бюллетень науки и практики / Bulletin of Science and Practice

В настоящее время широко охвачены объекты, в которых можно пренебречь дипольными и другими межмолекулярными взаимодействиями, и к которым относительно легко применима молекулярная модель Дебая. А объекты, в которых преобладает тип межмолекулярного взаимодействия в исходных компонентах (полярные жидкости с заметными диэлектрическими потерями, бинарные и другие системы растворов полярных жидкостей), изучены сравнительно мало и интерпретация степени влияния на общую релаксационную характеристику отдельных кинетических единиц и сил межмолекулярного взаимодействия по сравнению с чистыми жидкостями довольно ограничена. Причиной этого можно считать, в частности, трудности, возникающие при применении известных диэлектрических методов исследования этих систем при изучении систем [1-4].

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №8 2025

Материал и методика

Методические трудности, возникающие при применении известных диэлектрических методов исследования к указанным выше объектам исследования, привели нас к разработке нового вариационного метода исследования диэлектрических характеристик.

Методы диэлектрической радиоспектроскопии, основанные на изучении природы диэлектрической поляризации и процессов ее установления во времени под воздействием внешнего электрического поля, можно отнести к эффективным методам исследования жидкостей. При этом, если равновесные (статические) диэлектрические свойства вещества отражают суммарный вклад всех кинетических единиц, составляющих вещество, то динамические свойства наглядно демонстрируют долю каждой из них, обусловленную структурными, фазовыми и конформационными особенностями и состоянием вещества [5-7].

Результаты и их обсуждение

В результате проведенных исследований был предложен вариационный метод определения диэлектрических коэффициентов полярных жидкостей на СВЧ, основанный на измерении коэффициента стоячей волны ηm при толщине слоя жидкости lm в короткозамкнутой на конце измерительной ячейке, при которой отражение электромагнитной волны минимально. Согласно этому методу для расчета диэлектрических коэффициентов используются длина электромагнитной волны λd и фактор потерь исследуемой жидкости, определяемой при помощи номограмм по экспериментально найденным значениям ηm и lm. В предлагаемом варианте этого метода отпадает необходимость в вычислении промежуточных значений λd и фактора потерь. Диэлектрические коэффициенты жидкостей рассчитываются при помощи универсальных номограмм не посредственно по найденным экспериментальным значениям ηm и lm.

Рассмотрим для общности волновод, заполненный средой с комплексным значением диэлектрической проницаемости ξ=ξ'-iξ''. Порядок вывода сохраняет свое значение и для случая распространения электромагнитной волны в коаксимальных системах или в свободном пространстве, заполненным исследуемой средой. Тогда следуя (1) имеем,

ξ1= u^-2(1-y²) (1)

ξ2= 2yu^-2 (2)

где ξ1= ш , ξ2= й; “ = ^; У = ^|; Д= arctg ^,

λ, λв, λд — длины электромагнитных волн соответственно в свободном пространстве, в пустом волноводе и в волноводе, заполненном исследуемой средой; λ0 — критическая длина волны, определяемая размерами волновода. В случае распространения волн типа ТЕМ λ→сои p=0. Для связи значений и в (1) и (2) с экспериментально измеряемыми параметрами рассмотрим случай отражения распространяющихся в пустом волноводе электромагнитных волн от отрезка короткозамкнутой на конце линейной волноводной секции, расположенной в конце волноводного тракта и заполненный исследуемой жидкостью. Предполагается, что толщина жидкости l в волноводной секции регулируется. Для полярных жидкостей, обладающих поглощением в диапазоне СВЧ, зависимость коэффициента стоячей воды η в пустом волноводе от l к некоторому предельному значению η. Поэтому удобно в качестве измеряемых параметров, вводимых в (1) и (2), использовать значения ηm и lm, соответствующие экстремальным значениям зависимости η от l.. Согласно (1) , условие экстремума функции η от l сводится к следующему:

sh (4 ®y)sin (4 лх)         2yu

1—с/г(4лх)со5(4лх) (l-y2)- (l+ya )a где x=lm/λд (здесь lm — толщина слоя жидкости в волноводной секции, при которой имеет место минимум ил максимум амплитуды отраженной от ячейки электромагнитной волны). Из (3) следует, что в точке экстремума функции η от l u= (1+y2) R-1/2(4)

υ= x(1+y2) R-1/2(5)

2     L—сЛ(2Жгу)сов(4Жг)

где υ= lm/λв ; R=1-y2-2y×;

;

При этом экстремальные значения ηm описываются двумя функциями

_ Icth (2Xry)+yctg(2ia:)(6)

^m      th (.2Яху)-ytg^Xx)

_ I th (2»y)-ytf(2»i(7)

^m      cth (,2xicy)+yctg(2xx)

Последнее соотношение справедливо для значений x x1 и y sh(πx1y1)= -y1sin(πx1), соответствующего случаю ηm =1). Подставляя (4) в (1) и (2) имеем,

ξ1= 1   = R;

ξ2= 1 R

Полученные уравнения (5)-(9) содержат лишь функции двух вспомогательных параметров x и y в принципе устанавливают связь между диэлектрической проницаемостью ξ' и диэлектрическими потерями ξ'' жидкости в ячейке lm , при которой обнаруживается экстремум ηm и значение ηm, при этой толщине жидкости, при условии, что λ и λв известны. Однако, получить эту связь в явной форме невозможно из-за наличия в исходных уравнениях (5)-(9). В этих целях удобно использовать данные о η и l , соответствующие минимальным значениям зависимости η и l , поскольку при таких толщинах жидкости в ячейке снижаются погрешности измерения η, обусловленные паразитными отражениями волны от слюдяной прокладки и несовершенством конструкции короткозамыкающего поршня в измерительной ячейке. Кроме того, для полярных жидкостей, обладающих заметными диэлектрическими потерями в диапазоне СВЧ в зависимости η от l, как правило, обнаруживается лишь одно резко выраженный минимум η. С учетом этого, в дальнейшем ограничились установлением взаимосвязи между ξ' и ξ'' и экспериментальными данными о ηm и lm,, соответствующие первому минимуму зависимости η от l.

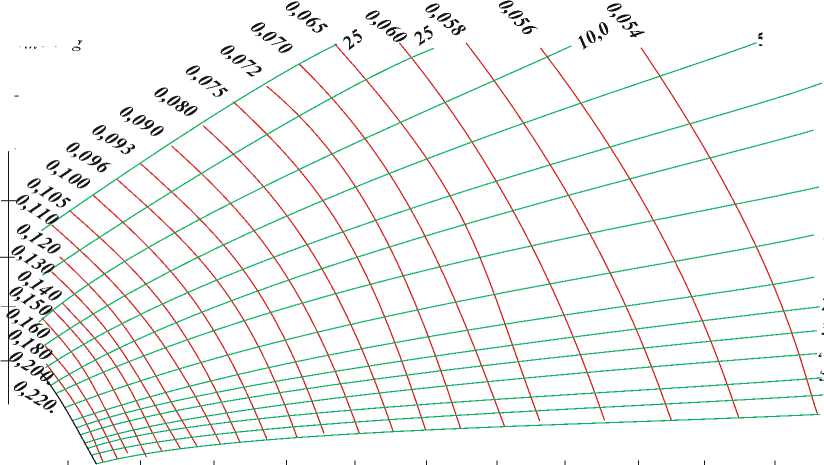
Для графического решения (5)-(9) ξ1, ξ2, υ и ηm были табулированы в интервале значений x 0,250-0,300 и y 0,05-0,50. При выборе интервала изменения x исходили из того, что расстояние первого минимума зависимости η от l от границы раздела воздух-жидкость в измерительной ячейке всегда больше λд /4 (2). Результаты вычислений были использованы далее для построения номограммы функций υ и ηm в плоскости координат ξ1 и ξ2.На рисунке представлены номограммы, построенные указанным способом, для расчета диэлектрических коэффициентов полярных жидкостей по данным измерений к.с.в. и толщины слоя жидкости в ячейке, соответствующей минимуму отражения волны. аналогичные номограммы при необходимости могут быть построены для последующих экстремумов зависимости η от l.

5,0

l m / Л g

ε 1

зЛ°°

2,50°

1,33°

1,0

1,5

2      4      6      8      10     12     14     16    18    20    22  ε 2

Следует отметить, что использование при построении номограмм приведенных параметров ξ1, ξ2, υ и ηm придает номограммам универсальный характер; они не зависят от частоты, при которой ведется измерение и могут быть применены при измерениях диэлектрических коэффициентов полярных жидкостей в свободном пространстве и в коаксиальных системах. Благодаря универсальным номограммам заметно упрощается методика вычисления ξ' и ξ''. Если известны экспериментальные значения υ = lm/λв; ηm в точке первого минимума зависимости η от l, то ордината точки пересечения двух кривых на рисунке, соответствующих данным υ и ηm , дает приведенное значение диэлектрических потерь ξ2 , тогда как абсцисса точки пересечения — приведенное значение ξ1, . Найденные значения ξ1, и ξ2 используются затем для подсчета ξ' и ξ'' .

Вывод

На основе экспериментальных данных рассчитаны дипольные моменты, времена релаксации, параметр распределения времени релаксации, вклады основных и дополнительных областей дисперсии, а также механизмы, ответственные за существование различных областей дисперсии. Все экспериментальные данные о диэлектрических свойствах и релаксационных характеристиках исследуемых объектов получены впервые.