Измерение характеристик и оценка возможностей видеокамер со сверхширокоугольной оптикой

Использование телевизионных камер со специальной сверхширокоугольной оптической системой позволяет получать панорамное изображение. В сочетании с методами видеоаналитики это дает возможность контролировать визуальную обстановку в поле обзора, соответствующего полусфере. При этом актуальным является вопрос оценки потенциальных возможностей панорамных ТВ-камер в плане обнаружения и распознавания объектов. Эти возможности связаны с разрешающей способностью ТВ-камер, которая определяется характеристиками оптической системы и светочувствительной матрицы.

Один из типов сверхширокоугольных объективов с углом зрения, который может превышать 180 градусов, получил название «рыбий глаз» (Fisheye). Конструкция объективов достаточно сложная и может включать 7–12 компонентов, например, как показано на рис. 1.

Передние 2–3 компонента представляют собой отрицательные мениски, что обеспечивает прохождение лучей, входящих в систему под большими углами. Остальные компоненты формируют резкое изображение на светочувствительной поверхности матрицы, положение которой совмещено с фокальной плоскостью объектива.

Несмотря на то что существует широкий ряд ТВ-камер со светочувствительными матрицами различных размеров, для работы в комплекте со сверхширокоугольной оптикой подходят не все. Это объясняется конструктивными особенностями модуля сенсора. В некоторых моделях камер

поверхность сенсора утоплена в пластиковое обрамление на расстояние, равное нескольким миллиметрам, как показано на рис. 2. Учитывая, что задний рабочий отрезок объектива типа Fisheye зачастую очень мал, не удается получить резкое изображение на поверхности матрицы.

Вторым обстоятельством является подбор пары объектив–матрица по оптимизации используемой светочувствительной поверхности. Здесь требуется найти компромисс между угловым полем объектива и числом полезных пикселов в изображении на матрице. В зависимости от размера формируемого на матрице изображения можно выделить 3 варианта, показанных на рис. 3:

• а )    диагональное или полнокадровое (full-frame);

• б )    обрезанный круг (cropped circle);

• в )    циркулярное (circular).

Расчеты, выполненные для матрицы с соотношением сторон 4:3, показывают, что эффективность использования пикселов в 100 % обеспечивается только в диагональном изображении (рис. 3, а ). Однако при этом угловое поле (FOV – Field of View) будет значительно меньше максимально возможного и составит около 60 % в вертикальном направлении и около 80 % в горизонтальном.

Для варианта обрезанного круга (рис. 3, б ) эффективность использования пикселов матрицы составит 90 %, при этом угловое поле в вертикальном направлении уменьшится до 86 %, а в горизонтальном будет равно 100 %.

Для циркулярного изображения (рис. 3, в ) угловое поле в любом направлении будет соответствовать максимальному значению, однако эффектив-

Гй

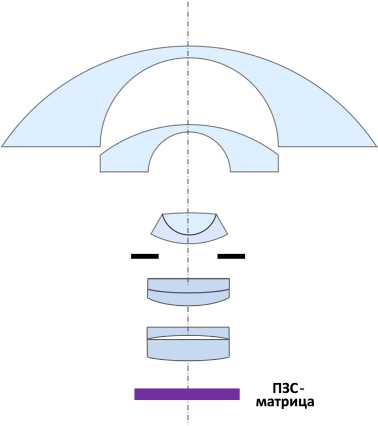
Рис. 1. Оптические компоненты объектива типа Fisheye

Fig. 1. Optical components of a Fisheye lens

а

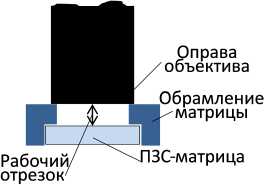
Рис. 2. Особенности конструкции светочувствительного сенсора

Fig. 2. Design features of the photosensitive sensor

б

ность использования пикселов матрицы будет составлять только 59 %. Для улучшения этого показателя используются специальные типы объективов со сложными функциями отображения [1].

в

Рис. 3. Варианты использования сверхширокоугольных объективов с матрицами формата 4:3 и доля используемых пикселов: а – full-frame – 100 %; б – cropped circle – 90 %; в – circular – 59 % Fig. 3. Variants of using ultra-wide-angle lenses with 4:3 format matrices and the proportion of pixels used: a – full-frame – 100 %; b – cropped circle – 90 %; c – circular – 59 %

1. Особенности формирования изображений в камерах со сверхширокоугольной оптикой

Формирование изображения на светочувствительной матрице ТВ-камеры с объективом Fisheye условно можно разделить на два этапа:

• 1)    Формирование сферического панорамного изображения. Это происходит в результате проекции всех видимых точек сцены на виртуальную сферическую поверхность, как показано на рис. 4;

• 2)    Формирование кругового панорамного изображения. Это происходит в результате проекции сферического изображения с виртуальной сферы на плоскую поверхность светочувствительной матрицы. Этот процесс отражен на рис. 5.

Как следует из модели, пространство объектов представляет собой 3-мерную декартову систему XOYZ, а двумерное пространство изображений X′O′Y′ совпадает с поверхностью матрицы. При этом точечный объект p, наблюдаемый под углом θ к оптической оси OZ, будет описываться трехмерными координатами p(x, y, z). Его проекция на сферу ps может быть описана двумя угловыми сферическими координатами – азимутальным углом ϕ и полярным углом θ, т. е. ps(ϕ,θ). Изображение p′ наблюдаемого объекта p(x, y, z) на поверхности ПЗС-матрицы образуется в результате проецирования точки ps(ϕ,θ) (рис. 5). Положение изображения можно описать декартовыми координатами p′(x′, y′) или полярными координатами p′(r, ϕ) в системе координат ПЗС-матрицы X′O′Y′, где r – расстояние от центра изображения; ϕ – угол поворота вектора r относительно оси O′X′. Для перехода к полярным координатам используются выражения:

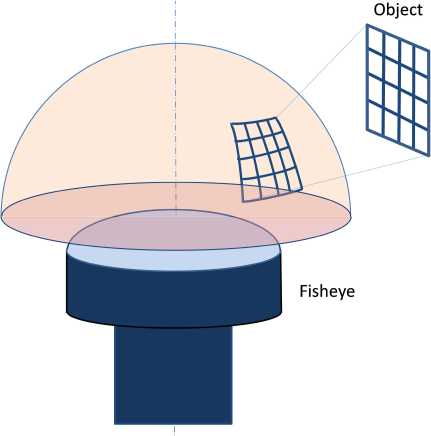
Рис. 4. Формирование изображения на поверхности виртуальной сферы

Fig. 4. Image formation on the surface of the virtual sphere

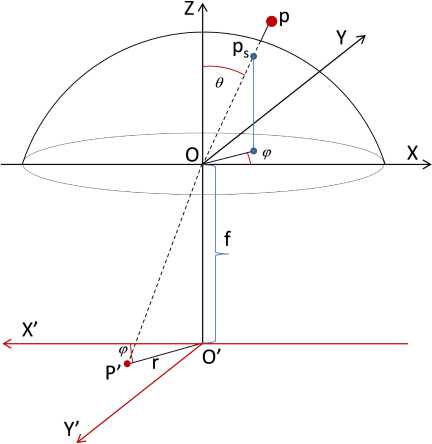
Рис. 5. Модель формирования кругового изображения на матрице

Fig. 5. The model of the formation of a circular image on the matrix

r = V (x ')2 + (y ')2; (1) ф = atan2( y', x'). (2) От полярных к декартовым координатам можно перейти по формулам x' = r cos ф, (3) y' = r sin ф. (4)

Изображение фрагмента сетчатого поля, расположенного в пространстве предметов (см. рис. 4), показано на рис. 6. Видно, что линии, которые на объекте были прямыми, на изображении будут искривлены, что приводит к нарушению геометрического подобия объекта и его изображения на матрице. Это объясняется тем, что линейное увеличение для участков объекта, находящихся от оптической оси на разных полярных углах 0 , будет уменьшаться при увеличении угла. Это приводит к возникновению геометрических бочкообразных искажений – отрицательной дисторсии [2].

Характер дисторсионных искажений описывается функцией отображения объектива (mapping function) [3]. Эта функция устанавливает зависимость радиального положения изображения точечного объекта r от фокусного расстояния объектива f и угла отклонения от оптической оси 0

r = F ( f , 0 ) (5) и может отличаться у объективов различных производителей. Для объективов Fisheye в литературе описаны следующие виды функций отображения [3]:

• -    equidistance: r = f * 0 ;

• -    orthogonal: r = f *sin 0 ;

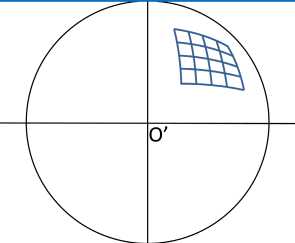
Рис. 6. Изображение фрагмента сетки на матрице

Fig. 6. Image of a grid fragment on a matrix

• -    stereographic: r = 2f * tan(0 / 2);

  - equisolid angle: r = 2f *sin(0 /2).

2.    Оценка информативности камер со сверхширокоугольной оптикой

Наиболее объективно оценить информативность ТВ-систем формирования изображений можно с помощью частотно-контрастных характеристик (ЧКХ), которые устанавливают зависимость контраста воспроизводимых деталей изображения от их пространственной частоты:

T ₍ N ) = ^ max ( N ) — ^ min ( N ) ,

^0max ^Omin где B (N), B(N) – максимальная и мини-max , min мальная яркости воспроизводимых деталей на частоте N; B0max, B0min – максимальная и минимальная яркости крупных деталей (с простран-

Рис. 8. Шумовое поле для измерения ЧКХ

Fig. 8. Noise field for measuring frequency response

КОГеП 2003 lens test Chart 5 mm 7086 pixels gamma = 1.5 ink spread = 0.25 Copyright (C) 2002 Norman Koren

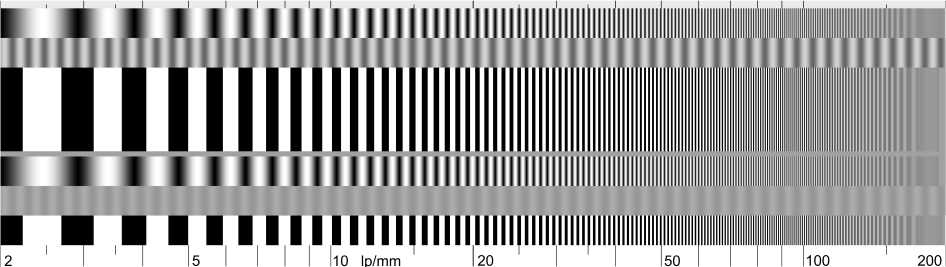
Рис. 7. Тест-объект с изменяющейся частотой штрихов для измерения ЧКХ

Fig. 7. Test object with variable stroke frequency for measuring the frequency response

ственными частотами, близкими к 0). В отличие от оптики, пространственную частоту здесь удобнее измерять в циклах на пиксель (cy/pixel). Она равна числу периодов чередующихся темных и светлых полос, уложенных вплотную друг к другу вдоль или поперек строки на светочувствительной матрице, деленному на число пикселей матрицы по горизонтали или вертикали (горизонтальная и вертикальная пространственные частоты соответственно).

Различие методов измерения ЧКХ связано в первую очередь с различием используемых для этой цели тест-объектов. Их можно разделить на три группы [4–7]:

• 1)    Тест-объекты, по которым непосредственно определяются значения яркости составляющих изображения различных пространственных частот, т. е. B ( N ). К ним относятся штриховые миры с синусоидальным или прямоугольным распределением яркости в штрихах. Пример одного из таких тест-объектов показан на рис. 7 [8];

• 2)    Тест-объект, представляющий собой изображение шумового поля, двумерный спектр распределения яркостей которого равномерен во всей полосе пространственных частот, например, как показанный на рис. 8. Методика расчета ЧКХ по изображению шумового поля рассмотрена в работе [9];

абв

Рис. 9. Тест-объекты для измерения функции рассеяния

Fig. 9. Test objects for measuring the scattering function

• 3)    Тест-объекты, по которым определяется функция рассеяния, использующаяся для последующего расчета ЧКХ. Такие объекты представляют собой изображения точечных или линейных объектов, спектр которых является сплошным. Примеры объектов такого типа показаны на рис. 9.

Вычисление ЧКХ производится путем анализа изображения тест-объекта, формируемого ТВ-камерой, требует значительных временных и вычислительных затрат и должно производиться в лабораторных условиях. При этом разброс результатов, полученных при использовании разных тест-объектов, достигает 30 %.

В связи с массовым появлением цифровых фото-и видеокамер был разработан международный стандарт ISO12233 с рекомендациями по измерению ЧКХ [10]. Первое издание ISO12233 появилось в 2000 г., а второе и третье – в 2014 и 2017 гг. Метод для измерения разрешающей способности по ЧКХ, описанный в стандарте, в качестве тест-объекта использует наклонную границу яркостного перепада, подобного показанному на рис. 9, б . Процедура измерения состоит из 10 шагов [11], основные из которых сводятся к следующему:

• –    выбор на изображении области интереса (ROI) с изображением наклонной границы;

  – сканирование строк выбранной области и их усреднение с выравниванием по нулевой интенсивности – получение пограничной кри-

• Рис. 10. Внешний вид измерительного стенда

Fig. 10. Appearance of a measuring stand

Рис. 11. Тест-объект №1 для измерения углового разрешения

Fig. 11. Test object No. 1 for measuring angular resolution

вой или функции рассеяния края (Edge Spread Function – ESF). Усреднение по нескольким строкам позволяет увеличить частоту дискретизации (oversampling), что в конечном итоге повышает пространственное разрешение анализируемых профилей;

– вычисление первой производной от полученной ESF, результатом которого будет функция рассеяния линии (Line Spread Function – LSF);

– дискретное преобразование Фурье (DFT) функции LSF позволяет получить искомую ЧКХ.

Выбор наклонной, а не вертикальной границы обусловлен двумя важными моментами, которые повышают точность измерений:

– при наклонной границе меньше вероятность того, что ее проекция будет неточно совпадать с положением пикселов матрицы;

– возможность сравнительно простого метода увеличения частоты дискретизации.

Поскольку характеристики разрешения оптической системы неравномерны по полю изображения, вычисление ЧКХ требуется выполнять как для центральных, так и для периферийных участков растра. Причем для получения сопоставимых результатов размеры изображений тест-объектов должны быть одинаковыми. В случае использования сверхширокоугольных камер это можно реализовать только на специальном стенде.

3.    Экспериментальные исследования

Для выполнения экспериментальных исследований был изготовлен специальный лабораторный стенд. Прототипом стенда является установка, описанная в статье [12]. Лабораторный стенд представляет собой часть цилиндра высотой 400 и радиусом 750 мм, установленного на поверхность горизонтальной столешницы. Поверхность цилиндра охватывает угол в 220 градусов, а оставшиеся 140 градусов в передней части отсутствуют. Испытуемая камера располагается горизонтально, причем оптический центр объектива совмещается с геометрическим центром цилиндра. При выполнении этого условия внутренняя поверхность цилиндра будет равноудалена от оптического центра на 750 мм, ее можно считать узкой частью сферы и размещать на ней тест-объекты. При этом высота расположения камеры не будет влиять на результаты измерений. Общий вид измерительного стенда представлен на рис. 10.

Для выполнения измерений были изготовлены два вида тест-объектов:

• 1)    Тест-объект № 1 для измерения углового разрешения – представляет собой чередующиеся вертикальные черные и белые полосы шириной 2 градуса. Полосы, угловое расположение которых соответствует 0, 60, 80, 90 градусам, имеют мет-

  

  Рис. 12. Тест-объект № 2 для измерения ЧКХ

  Fig. 12. Test object No. 2 for measuring the frequency response

  
  
  

  Рис. 13. Исходное изображение для расчета углового разрешения камеры

  Fig. 13. The original image for calculating the angular resolution of the camera

  
  
  

  Рис. 14. Область интереса и выделенная для расчетов строка

  Fig. 14. Area of interest and line allocated for calculations

  
  

ки в виде белых треугольников, как показано на рис. 11;

• 2)    Тест-объект № 2 для измерения ЧКХ представляет собой пять наклонных черных прямоугольников на белом фоне. Ширина прямоугольника соответствует 16 градусам, а его вертикальная черно-белая граница имеет наклон около 6 градусов, что соответствует рекомендациям стандарта ISO12233. Вид тест-объекта показан на рис. 12. Прямоугольники размещаются на внутренней поверхности цилиндра на нужном угловом расстоянии от центра.

Важными этапами экспериментального измерения характеристик являются:

• –    установка равномерной освещенности тест-объекта в пределах всего поля зрения камеры;

• –    отключение в испытуемой камере автоматической регулировки усиления и автоматического повышения резкости (sharpening);

• –    уровень белого должен быть отрегулирован так, чтобы не наблюдалось насыщения на ярких участках.

• 3.1.    Расчет углового разрешения

После этого в ЭВМ вводятся десять кадров с изображением тест-объекта № 1 и десять кадров с изображением тест-объекта № 2, из которых формируются усредненные тестовые изображения. Дальнейшие действия по расчету характеристик производятся на компьютере.

Для расчета характеристик углового разрешения была создана программа в среде MATLAB, позволяющая производить вычисления в интерактивном режиме. Основные шаги расчета приводятся ниже.

• 1.    На загруженном изображении (рис. 13) выбирается область интереса, соответствующая положению теста-объекта № 1, которая вырезается из исходного (рис. 14).

  

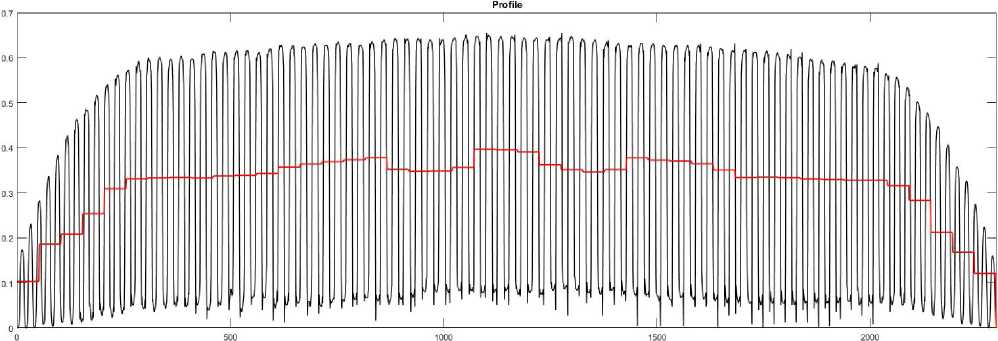
  Рис. 15. Профиль выделенной строки и порог бинаризации

  Fig. 15. The profile of the selected line and the threshold of binarization

  
  
  

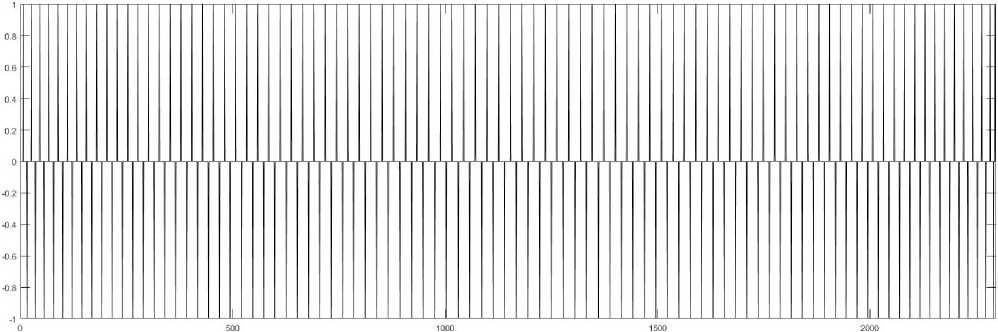
  Рис. 16. График первой производной бинаризованного профиля строки

  Fig. 16. Graph of the first derivative of a binarized line profile

  
  

• 2.    На области интереса выбирается строка, которая совпадает с вертикальным положением оптической оси камеры. Выбранная строка подсвечивается на изображении тест-объекта.

• 3.    Для выделенной строки строится профиль, который выводится в графическое окно (рис. 15). Все угловое поле разбивается на участки по 4 градуса, для которых вычисляется среднее значение профиля, выводимое в то же графическое окно.

• 4.    Полученный профиль преобразуется в бинарные значения по порогу, равному найденным средним значениям, после чего вычисляется первая производная (см. рис. 16). Каждый положительный пик графика производной соответствует положению левого края белой полоски на тест-объекте, т. е. расстояние между пиками равно периоду следования белых полос. Этот период равен двум угловым градусам.

• 5.    В завершение производится подсчет числа пикселов между положительными пиками графика производной. Для получения углового разреше-

• ния RS нужно найденное число разделить пополам и построить график (см. рис. 17).

Анализ построенного графика для камеры с КМОП сенсором Sony IMX179 размером 1/3.2" с числом пикселов матрицы 3264 х 2448 и объективом Lux.1.19 Visual Feast показывает, что угловое разрешение изменяется незначительно для диапазона полярных углов от 0 до 45 градусов и лишь при углах, превышающих 75 градусов, заметно снижается. Тем не менее для выполнения расчетов разделим поле зрения на три диапазона, в пределах которых угловое разрешение камеры RS можно считать неизменным и пользоваться усредненными значениями:

• 1)    центральные области с полярными углами 0–20 градусов – RS = 13,8 px/degree;

• 2)    средние области с полярными углами 21–45 градусов – RS = 13,25 px/degree;

• 3)    периферийные области с полярными углами 46–80 градусов – RS = 11, 5 px/degree .

• 3.2.    Расчет частотно-контрастных характеристик

Построенный график по сути является графиком функции отображения, поскольку показывает,

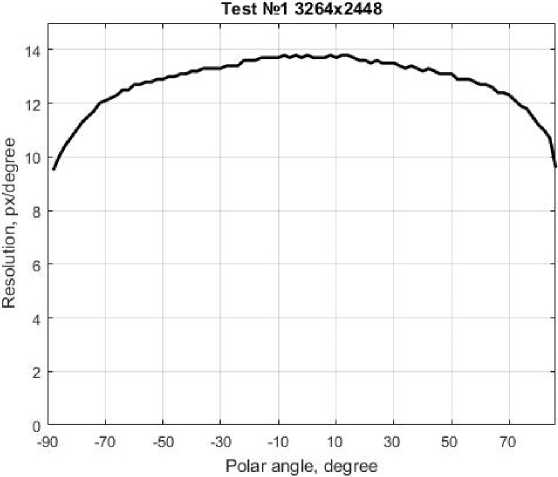
Рис. 17. Зависимость углового разрешения от полярного угла

Fig. 17. The dependence of the angular resolution on the polar angle на сколько пикселов перемещается точка на изображении при изменении полярного угла, под которым наблюдается объект, на один градус. Этот же график позволяет определить пиксельные размеры объекта на изображении в зависимости от угловых размеров объекта. Полученные характеристики необходимо учитывать при расчете ТВ-систем.

Для расчета ЧКХ используется тест-объект № 2, который размещается на внутренней поверхности стенда под углами 0, 45 и 75 градусов от оптической оси камеры, как показано на рис. 18.

Каждый из пяти черных прямоугольников на белом фоне представляет собой наклонный край, который используется для вычисления ЧКХ, согласно методике, рекомендованной стандартом ISO12233. Шаги этой процедуры описаны выше. Для вычислений использовалась программа sfrmat2.m, работающая в среде MATLAB, созданная P.D. Burns [11]. Рассчитанные ЧКХ для центральной, средней и периферийной областей поля зрения с углами 0, 40 и 75 градусов приведены на рис. 19.

Рис. 18. Кадр для расчета ЧКХ камеры

Fig. 18. Frame for calculating the frequency response of the camera

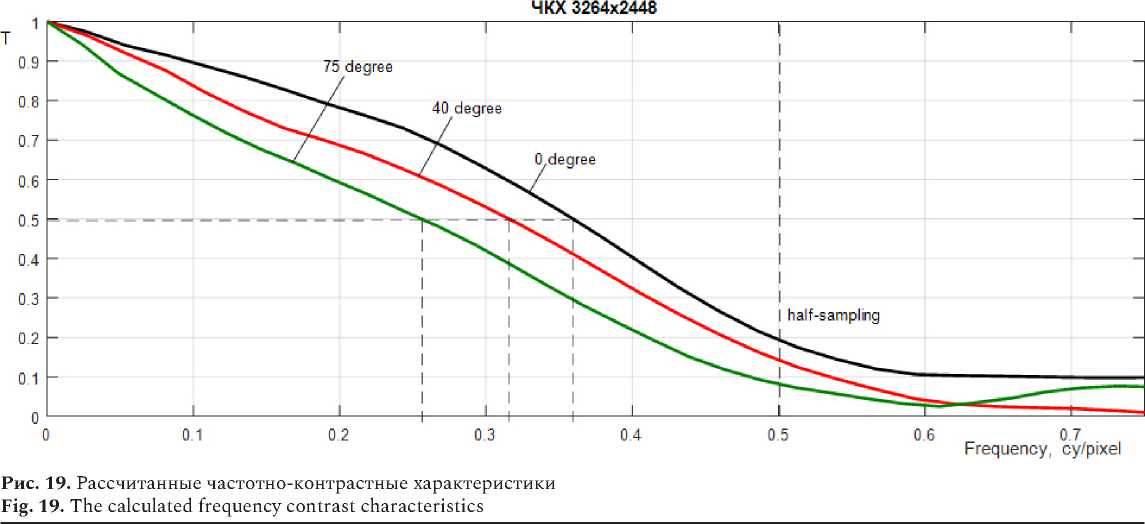
Таблица Table

Полярный угол 9 , град	Усреднен. угловое разрешение RS , px/град	Пространств. частота N 0 5, cy/px ,	Миним. размер объектов L 0,5, px	Миним. угловой размер P min , град	Миним. линейный размер на D = 3 м V min - мм	Миним. линейный размер на D = 5 м V min - мм
1	2	3	4	5	6	7
0–20	13,8	0,36	1,39	0,1007	5,273	8,788
21–45	13,25	0,32	1,56	0,1177	6,163	10,271
46–80	11,5	0,255	1,96	0,1704	8,733	14,556

4. Оценка возможностей видеокамер со сверхширокоугольной оптической системой

Рассчитанные характеристики углового разрешения RS и частотно-контрастные характеристики T ( N ) позволяют оценить потенциальные возможности видеокамер в плане обнаружения объектов заданных линейных размеров. Такую оценку целесообразно выполнять в следующей последовательности.

• 1.    Используя графики ЧКХ, определяем пиксельный размер деталей изображения на матрице, при котором будет обеспечиваться заданный контраст. Например, контраст, равный половине максимального значения T _{0 5} для углов зрения 0-20 градусов, будет обеспечиваться черно-белыми линиями с пространственной частотой N 0 5 <  0,36 cy/px. Это означает, что пара черно-белых линий с минимальным размером

• 2.    Используя значения усредненного углового разрешения RS и минимального пиксельного размера объектов L 0 5 можно перейти к минимальным угловым размерам объектов

• 3.    Минимальный угловой размер позволяет рассчитать минимальные линейные размеры объектов V _min, которые находятся на определенной дистанции D от оптического центра камеры, по формуле

L0,5 = 1 / T0,5 = 2,77 px будут различимы с контрастом не менее 0,5. Таким образом, предельный размер черных или белых объектов, при котором обеспечивается контраст T = 0,5, будет составлять L05/2 = 1,39 px. Рассчитанные аналогично характеристики для углов 40 и 75 градусов сведем в столбец 3, 4 таблицы, которая приведена ниже.

P min = L 0,5 / RS .

^V min = D tg ₽ min .

Рассчитанные значения минимального углового размера P min и минимальных линейных размеров объектов V min для дистанции 3 и 5 м представлены в столбцах 5, 6 и 7 таблицы.

Заключение

Использование видеокамер с оптической системой типа Fisheye, безусловно, является перспективным для решения ряда многих прикладных задач. Однако грамотный подход к решению таких задач должен начинаться с оценки потенциальных возможностей используемых видеокамер.

Изложенные в разделе 3 методики измерения характеристики углового разрешения и частотноконтрастной характеристики позволяют получить количественные оценки информативности системы формирования изображений.

Изложенная в разделе 4 методика оценки возможностей видеокамер позволяет легко рассчитать допустимую дистанцию до объектов интереса, если известны линейные размеры этих объектов. Результаты экспериментальных исследований показали, что ее с успехом можно использовать для практических расчетов при разработке систем:

• -    контроля и регистрации визуальной обстановки в помещениях с помощью одной неподвижной ТВ-камеры;

• -    контроля и регистрации визуальной обстановки вокруг перемещающихся устройств, например мобильных роботов;

• -    визуального осмотра труднодоступных скрытых полостей, например баков, емкостей и т. п.;

  – визуальный осмотр внутренних поверхностей трубопроводов.