Измерение и управление площадью кристалла на установке вытягивания германия

Г3 (x) = V3n (x) + Kv Ay ,(1)

T3 (x) = ТзП (x) + At JAydx,(3)

Ay=X-   - XT ’

A c

K = B " ^y A c

3 T

_ 12

D ⎤

, d 3 _

где К- пропорциональный коэффициент регулирования по скорости; 4 - интегральный коэффициент регулирования по температуре; V (х), Т (х) - программное задание закона изменения технологических параметров; V_з(х), Т (х) - общее управление технологическими параметрами; A у - сигнал управления; х - перемещение вдоль оси кристалла; К_у - уставка заданного диаметра кристалла; X - перемещение затравки с дискретностью отсчета A _з; А - перемещение тигля с дискретностью отсчета A _т; D - внутренний диаметр тигля; р - удельная плотность твердого материала; р _ж- удельная плотность жидкого материала; d - заданный диаметр выращиваемого кристалла; А - коэффициент масштабирования; В - коэффициент умножения уставки; A - дискретность отсчета перемещения затравки; A - дискретность отсчета перемещения тигля; d_з - заданный диаметр выращиваемого кристалла.

Программное задание по скорости и температуре Vзп(х), Тзп(х) в микропроцессорных системах производится за счет автоматического расчета и ввода в программу управления кадровой системы управления по данным параметрам.

При отработке микропроцессорных систем выращивания монокристаллов германия выяснилось, что вычисление сигнала управления Ay по выражению (4) приводит к сложной периодической ошибке измерения до 4 % (за счет погрешностей винтовых передач по перемещению кристалла и тигля). С целью повышения точности измерения текущей площади кристалла и максимального устранения ошибки измерения была найдена новая математическая модель для измерения площади кристалла. Ниже приводится математический аппарат вычисления сигнала управления на основе широтной модуляции сигнала датчика уровня.

Время паузы после замыкания контактного датчика в контактном методе At и время ускоренной скорости движения тигля после размыкания датчика At ^ , а также число циклов К_ц по замыканию и размыканию датчика можно представить следующими выражениями:

A t _д ( d ) = A t

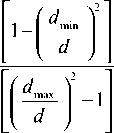
К =---T---.

^D ( A t д +A t ) ^,

где A z - время движения тигля с замедленной скоростью V^JM после замыкания датчика; A t_д - время движения тигля с ускоренной скоростью К_тм после размыкания датчика; К - число циклов замыкания и размыкания датчика за время Т_ц; Т_ц - период оценки сигнала управления (время отработки заданного количества импульсовА^); d_max - максимальный допустимый диаметр выращиваемого кристалла, с соблюдением которого выполняется

ного значения рабочего диапазона диаметра At(d_тp) по выражению

LT

А t ( d) = т =         ,

^ТР        Х_та E

где E = —---

M ^⎛1 - 1 ⎜_{⎝ C}

.

условие, при котором датчик и экран сомкнутся после размыкания; dmin - минимальное допустимое значение диаметра кристалла, при котором соблюдается условие

отставания экрана от датчика после замкнутого состояния; d- текущий диаметр кристалла.

Система автоматического управления за счет регулирования текущей площади кристалла по сигналу управления обеспечивает диапазон изменения диаметра в со

ответствии с выражениями

d = d

PP ³

d mp            pp ,

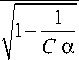
d = d„  ,— = d  ,— mp max            3

M M

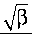
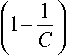
Число циклов замыкания и размыкания Кц датчика уровня можно представить следующим образом:

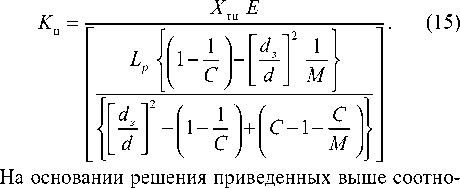
шений сигнал управления Dy можно выразить через формулы

С

C -1 - - ,(16) M ⎠

где d_pp - максимальный рабочий диаметр; d_mp - минимальный рабочий диаметра; а - коэффициент рабочего максимального диаметра ( а = 2); в - коэффициент рабочего минимального диаметра (в = 2,5); С-коэффициент увеличения скорости подъема тигля; M - коэффициент

уменьшения скорости подъема тигля.

Выражение (5) времени ускоренной скорости подъема тигля A t_д при различных значениях рабочего диапазона диаметра кристалла можно представить в виде

⎛ C α ⎞

C α-α-

M

^А ' ' ( d pp ⁾ ' t ^     ( а- 1 )     ' •         ⁽¹⁰⁾

А t ( d ₃) = А t 1 C -1 - ^— ,          (11)

⎝ M ⎠

β-1

^А t « ⁽ d mp ) = ^А t (^ '

Если задаться условием максимально допустимого

размыкания уровня расплава в контактном методе управления L _p (1...2 мкм), то выражение времени замедленной скорости подъема тигля A t(d) примет вид

L p

∆ t ( d )=

^⎛⎜ V p ( d )

-

V тм

LT

Р ц

" d^ 1 2

⎢_{⎣ d} ⎥_⎦

M

тц

-

⎛

_ d " ⎢⎣ d ⎦

2

\

M ^⎛1 - 1 ⎜_{⎝ C}

где L_p - максимально допустимое значение изменения уровня расплава.

В качестве основной оценки выберем оценку време-

ни замедленного движения тигля для крайнего минималь-

^А У = ^А t д ^{( d} ) ^{- А} t д ^{( d} з ) = ^А t д ^{( d} )^{- т}

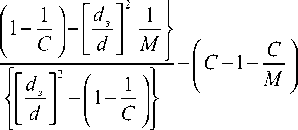
Для программирования сигнала управления в микропроцессорной системе управления выращиванием монокристаллов германия применен алгоритм управления (рис. 2), который заключается в том, что в системе управления в момент замыкания контактного датчика выдерживается программная пауза т замкнутого и последующая пауза т разомкнутого искусственных состояний датчика уровня, после чего происходит вычисление сигнала управления Ау на основе подсчета длительности паузы A t_дм(d) до момента первого замкнутого состояния датчика уровня:

Г _ С 1

А у = А t _м( d )-т^ C - 2 ^ .

^д [ м\

Выражения (16-18) являются математической моделью вычисления сигнала управления на основе широтной модуляции сигнала датчика уровня, которая базируется на задании базовых констант контактного метода измерения площади кристалла С, M, в , а , L^A^, d^.

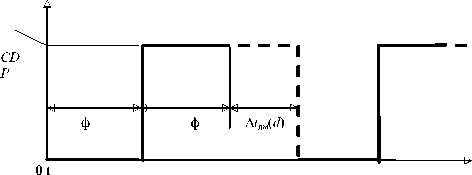
Рис. 2. Временная диаграмма работы датчика уровня: CD - работа контактного датчика уровня (Р - датчик разомкнут)

Графики работы микропроцессорных установок выращивания монокристаллов германия диаметром 104 мм, где была проведена отработка данной методики показаны на рис. 3 и 4.

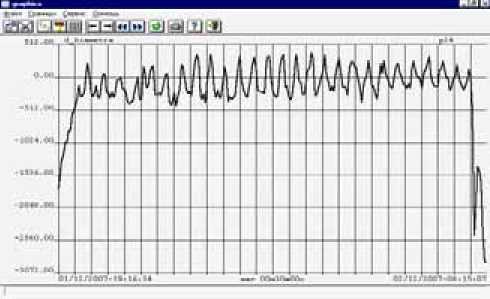
Рис. 3. График изменения сигнала управления Д у (d_Diametra) на установке № 24

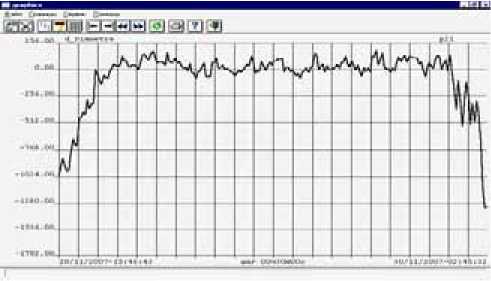
Рис. 4. График изменения сигнала управления Ду (d_Diametra) на установке №21

Работа установки вытягивания германия №21 (рис. 4) производилась с применением программы вычисления сигнала управления Д у на основе рассмотренной выше методики с широтной модуляцией сигнала датчика уровня. Качественное сравнение сигналов управления с сигналом управления на установке № 24 (рис. 3) наглядно демонстрирует сложную периодическую ошибку измерения за счет погрешностей винтовых передач по перемещению кристалла и тигля на установке № 24 и ее устранение на установке №21. Данная ошибка измерения приводила к колебанию полученного после вытягивания готового кристалла по диаметру на установке № 24 в пределах 2-4 %.

Внедрение данного метода вычисления и управления диаметром кристалла на установке № 21 позволило дове сти точность стабилизации площади кристалла диаметром 104 мм до 0,5 %, что подтверждено актом внедрения в производство ФГУП «Германий». Анализ точности произведен на основе измерения готовой продукции.

Особенностью предложенного метода измерения является то, что он позволяет стабилизировать площадь кристалла, что является актуальным при выращивании кристаллов германия кристаллографического направления «100», имеющих значительную огранку приближающую форму монокристалла германия в сечении к квадратной.

Таким образом, разработанная математическая модель позволила организовать производство монокристаллов германия направления «100» и диаметром 104 мм с воспроизведением формы (площади) готового монокристалла с точностью до 0,5 %.