Измерение эффективной поверхности рассеяния объектов с электродинамически связанными элементами приемо-передающими системами с синтезированием апертуры антенн

В последнее время в связи с постоянно растущими требованиями к точности и детальности измерения радиолокационных характеристик (РЛХ) объектов все более актуальной становится проблема повышения информативности средств измерений, решению которой посвящена весьма обширная литература [1; 2].

Среди множества направлений совершенствования средств измерений наиболее эффективные связаны с получением и совместной обработкой результатов многомерных измерений (по пространству, частоте и времени) на базе новой радиолокационной технологии, основанной на получении и совместной обработке результатов измерений (САОРИ) параметров сигналов1.

При реализации такой технологии существенно упрощается радиотехническая часть средств измерений, поскольку в них используются виртуально управляемые антенные решетки. Кроме того, значительно повышается качество средств измерений, поскольку им становятся присущи все достоинства цифровых устройств [2]. Это становится возможным благодаря тому, что, в отличие от традиционных средств измерений, в которых операции по получению радиолокационной информации (формирование диаграмм направленности передающей и приемной антенн, излучение и обработка сложных сигналов и т. п.) осуществляются с помощью физических устройств, в соответствии с новыми технологиями они выполняются программно (виртуально) на ЭВМ [2].

Существенная особенность построения многоканальных измерительных систем с позиций простоты конструкции и достижения высокой информативности состоит в способе получения многоканальной информации. Так, измерительные системы с синтезированием передающей и приемной антенн существенно более просты в конструктивном исполнении, однако они имеют более ограниченные возможности по измерению РЛХ, особенно объектов сложной формы и неоднородных электродинамических свойств.

Целью настоящей статьи является сравнительная оценка информационных возможностей измерительных систем с синтезированными и реальными многоканальными апертурами при измерении ЭПР сложных объектов с электродинамической связью отдельных элементов.

Постановка задачи

Рассмотрим случай измерения ЭПР сложного пространственно протяженного объекта измерительной системой с многоканальными реальными и синтезированными передающей и приемной антеннами. В ориентации на метод относительных измерений будем считать, что величина ЭПР пропорциональна интенсивности входного сиг

нала оптимального приемника [3]. Измерения проводятся с использованием многоканальных пространственных квазимонохроматических сигналов с центральной частотой to g в присутствии белого гауссовского шума при большом отношении сигнал/шум. Для оценки информационных возможностей ППС со сканированием приемопередающим элементом сравним получаемые при этом результаты с результатами, получаемые идеализированной ППС с заполненными апертурами приемной и передающей антенн.

Модель сигнала

Воспользуемся простейшей моделью пространственно протяженного объекта с электродинамически связанными элементами в виде двухточечной цели [4]. Результирующая модель сигнала при этом имеет вид [2]

S ⁽ r , р) = An Su + A 22 S 22 ⁺ A 12 S 12 ⁺ A 21 S 21 , (1) где A 11 , A 22 - амплитуды отраженных сигналов от первого и второго отражателей; A 12 - амплитуда сигнала, прошедшего путь: «излучатель - первый отражатель – второй отражатель – приемник»; A ₂₁ – амплитуда встречного сигнала;

S 11 ( г , р, ^) = exp { - ik [ R ( r , ^) + R (^, p) ] } ; (2) S 22 ^{( r} , p, ^) = exp { ^- ik [ ^{R ( r} , ^2) + ^{R (}^ 2 , p) ] } ; ⁽³⁾ S ₁₂ ( r , РЛ1, ^₂ ) = e~ ^ exp { - ik [ R ( r , § 1) + R <^ ₂ , p) ] } ; (4) S ₂₁ ( r , p, ^1Л ₂ ) = e ^- i ° exp { - ik [ R ( r , § ₂ ) + R (§ 1 , p) ] } ; (5) Ф = kR (^,^2) — фазовый набег сигнала на пути распространения его между отражателями; r , р , § 1 , § 2 — координаты точек положения излучателя, приемника, первого и второго отражателей; R ( Х 1 , x 2 )- расстояние от точки х 1 до точки Х 2 ; k — 2п / X - волновое число, X - длина волны.

Алгоритм оптимальной обработки сигналов2

При проведении измерений в присутствии аддитивного гауссовского шума и при большом отношении сигнал/шум сигнальная составляющая оптимального фильтра, характеризующая величину ЭПР двухточечного объекта со связанными отражателями, в соответствии с результатами работы [2] равна3

¹ ^ =    f⁽ A 11 S 11 + A 22 S 22 ⁺ A 12 S 12 ⁺ A 21 S 21 ) ^х

N 0

*

*

*

*

х ( A 11 S 1 + A ₂₂ S ₂₂ + A ₁₂ S ₁₂ + A ₂₁ S ₂₁ ) d r d p , где * - обозначение комплексно сопряженной величины.

В соответствии с (6) алгоритм получения оценки ЭПР двухточечного объекта со связанными элементами состоит в вычислении суммы корреляционных интегралов всех координатных функций S ij , i , j = 1,2.

С учетом ранее опущенных (для упрощения вида аналитических выражений) апертурных функций передающей T ( r ) и приемной I (р) антенн, а также описания амплитудно-фазового распределения поля излучения E ( r ) корреляционные интегралы, входящие в выражение (6) для оценки ЭПР, принимают вид

S ij = f f |W)f I< E ( r )²

( P )( Q )

*

х

х S ij ( r , р) S kl ( r , р) d r d p.

Полагая далее функции T ( r ), I (p), E ( r ) равными единице, корреляционные интегралы координатных функций запишем в следующем виде.

• 1.    Случай наличия в ППС реальных многоканальных передающей и приемной антенн:

• 2.    Случай ППС с синтезированной апертурой передающей и приемной антенн.

I 1 = ff S t1 S *1 d r d p = A 21 S r S p ,	(8)
1 2 = ff S 11 S 22 d r d P = A 11 A 22 I r ( § 1^2 ) I p (^ 1 , § 2 ),	(9)
1 3 = ff S 11 S 12 d r d P = e ^ A 11 A 12 Ir1 p ( § 1 ,^ 2 ),	(10)
1 4 = ff S 11 S 21 d r d P = e ^ A 11 A 21 I r (^ 1 ,§ 2 ),	(11)
1 5 = ff S 22 S 11 d r d P = 1 2 ,	(12)
1 6 = ff S 22 S 22 d r dR = A 2 S r S p ,	(13)
1 7 = ff S 22 S 12 d r dP = e^ A 22 A 12 I r (^ 1 , § 2 ),	(14)
1 8 = ff S 22 S 21 d r dP = e Ф A 22 A 21 I p (^ 1 ’ § 2 ),	(15)
1 9 — ff S 12 S u d r d p — 1 3 ,	(16)
1 10 = ff S 12 S 22 d r dP = I 7 ,	(17)
1 11 = ff S 12 S 12 d r dP = S r S p ’	(18)

³ Интегрирование здесь и далее выполняется по областям задания передающей p и приемной Q антенн с учетом значений их апертурных функций - ^ ( r ) и I (р) соответственно.

Физика волновых процессов и радиотехнические системы. 2020. Т. 23. № 1. С. 45–51 Physics of Wave Processes and Radio Systems, 2020, vol. 23, no. 1, pp. 45–51			47
I 12 = JJ S 12 S 21 d r d P = A 12 A 21 I r (^ 1 ,^ 2 ) I p ( § 1 , § 2 ),	(19)	1 11 = J S 12 S 12 d P = A 12 S p ,	(40)
*               * 1 13 —     s 21 S 11 d r dp — 1 4 ,	(20)	1 12 = J S 12 S 21 d P = A 12 A 21 S p ,	(41)
1 14 = JJ S 21 S 22 d r d P = I 8 ,	(21)	*                            * 1 13 = J S 21 S 11 d p = e   A 21 A 11 I p (^ 1 ,^ 2 ),	(42)
1 15 = JJ S 21 S 12 d r d P = 1 12 ,	(22)	*           - i m           */„ 1 14 = J S 21 S 22 d P = e   A 21 A 22 I p ( § 1,^2 ),	(43)
1 16 = JJ S 21 S 21 d r d P = A 21 S r S p ,	(23)	*           * 1 15 = J S 21 S 12 d P = 1 12 = A 12 A 21 S p ,	(44)
где I r (^ 1^2 ) = JJ exP [ ik [ R ( r , ^1 ) - R ( r , ^2 ) ]] d r ,	(24)	1 16 = J S 21 S 21 d P = A 21 S p , где 4	(45)
I p ( § 1^2 ) = JJ exP [ - ik [ R (P, ^1 ) - R (P, § 2 ) ]] dP’	(25)	I c (^ 1 , §2) — J exp { - ik 2 [ R (p, 8 1 ) - R (p, e 2 ) ] } d p,	(46)

S r , S p - площади передающей и приемной антенн.

Сравним полученные выражения для идеализированной измерительной системы с аналогичными выражениями для ППС с синтезированной апертурой передающей и приемной антенн.

В рассматриваемом случае координатные функции, корреляционные функции которых определяют составляющие сигнальной функции, выглядят как

S11 (р) = exp{-ik 2 R (р, 81)},(26)

S 22(р) = exp{-ik 2 R (р,е2)},(27)

S12 (р) = exp {-ik [ R (p, 81) + R (p, e2)]},(28)

S 21 (p) = exp {-ik [ R (p, e2) + R (p, 81)]}.(29)

При этом корреляционные интегралы имеют аналогичные аналитические выражения, как для ППС с реальными антеннами:

1 1 = J ^S 11 ^S 11 ^dP ^— A 11 S p ,

I 2 = J ^S 11 ^S 22 ^d P = A 11 A 22 I n ⁽^ 1 ,^ 2 ),

I 3 = J ^S 11 S 12 d P = e^A 11 A 12 I p ⁽^ 1 , § 2 ),

I 4 = J ^S 11 ^S 21 d P = e ^ A 11 A 21 I p ⁽ § 1 , § 2 ),

**/f

I 5 = J S 22 ^S 11 d P = A 11 A 22 I c ⁽^ 1 ,^ 2 ),

I 6 = J ^S 22 ^S 22 d P = A 22 S p ,

**

I 7 = J ^S 22 S 12 d P = e A 22 A 12 I p ⁽^ 1 ,^ 2 ),

I 8 = J ^S 22 ^S 21 d P = e^ A 22 A 21 1 p ( § 1,^2 ),

I 9 ^— J S 12 ^S 11 d P = e ^A 12 A 11 1 p⁽^ 1 ,^ 2 ),

• *          — im

1 10 = J S 12 S 22 dp = e   A 12 A 22 I p⁽^51 , § 2 ),

а функция I p (^,^2) определяется выражением (25).

Анализ корреляционных интегралов для ППС с реальными и синтезированными антеннами в частных случаях.

• А. Измерение ЭПР точечного объекта.

В рассматриваемом случае

A 12

= A 21 = A 22

= 0.

После преобразований получим:

– для ППС с реальными антеннами

1 1 = A n S r S p ,

• - для ППС с синтезированными апертурами ан-

• тенн

• I 1 = A n S p .

То есть результаты измерения ЭПР точечных объектов, получаемых измерительными системами с реальными и синтезированными антеннами (с учетом нормировки), совпадают.

Б. Измерение ЭПР двухточечного объекта с независимыми отражателями ППС с реальными антеннами.

Полагая, что электродинамическая связь между элементами объекта отсутствует ( A 12 = A 21 = 0), информационные составляющие выходного эффекта оптимального фильтра для измерительной системы с реальными антеннами, в соответствии с выражениями (8)–(25), имеют вид

11 = A21 SrSp,(47)

12 = A11A 22 Ir (§1,^2) Ip (§1, §2),(48)

15 = 12 = A11A22 Ir (^2) Ip G1M

I6 = A222Sr Sp.(50)

Объединяя эти выражения, получим

I a 1 ^{— (} A 11 + A 22 ) S r S p +

+ 2 A_u A 22 Re { I r (^,^ 2 ) I p ( § 1 ,^) } .

I ac ^{— (} A 21 ⁺ A 22 ) S p ⁺

+ 2 A_u A 22 Re { I c (^) I ^ (§ 1 ,^ 2 ) } .

Существо и физический смысл полученного результата можно определить при его рассмотрении применительно к классической схеме измерения ЭПР-объектов5.

Аналогичные рассуждения, как при анализе (26)–(45), приводят к следующему выражению для определения ЭПР двухточечного объекта и с неза-

висимыми отражателями:

Предположим, что размеры антенн настоль-

ко малы, что подынтегральные выражения для I r (i^,^) (24) и Для I p (^1 , § 2 ) (25) можно считать постоянными, тогда I a 1 (51) можно представить в виде⁶

I ac

. 1 2         2

— const S A 11 + A 22

+ 2cos

8 nA R 1

X J

I a 1 = ] A 21 + A 22 ) + 2cos2 n Г A R r + A R p it S r S p ,     (52)

I                                    X                          J

где A R r - разность расстояний на пути распространения сигнала от передающей антенны до отдельных отражателей § 1 и ^, A R _р - разность расстояний от отражателей ^, ^2 до приемной антенны.

То есть при проведении измерений ЭПР двухточечного объекта с независимыми отражателями с помощью ППС с синтезированными антеннами возникают систематические погрешности, связанные с удвоением пространственной частоты отражательных сигналов.

Г. Измерение ЭПР двухточечного объекта со связанными отражателями ППС с синтезирован-

При совпадении пространственного положения передающей и приемной антенн выражение (52) соответствует классической формуле для определения ЭПР двухточечного объекта с неизвестны-

ми отражателями

I a 1

I л 2 л 2 — const s A11 + A 22

+ 2cos

4 nA R 1

X ’

ными антеннами.

Сравнение информационных возможностей этих систем, ввиду сложности выражений для выходного эффекта систем измерений при наличии взаимной связи элементов, представляет собой достаточно сложную задачу. Кроме того, поскольку достоверные сведения об ЭПР двухточечного объекта с электродинамическими связанными

Таким образом, приемо-передающая измерительная система с многоканальными реальными передающей и приемной антеннами обеспечивает измерение ЭПР двухточечного объекта с независимыми отражателями.

В. Измерение ЭПР двухточечного объекта с независимыми отражателями ППС с синтезированными антеннами.

элементами в литературе отсутствуют, примем следующий подход к ее решению.

Во-первых, будем считать, что измерение ЭПР двухточечного объекта со связанными отражателями измерительной системой с реальными апертурами передающей и приемной антенн осуществляется точно7. Поэтому оценку достоверности результатов измерений, получаемых ППС

Для ППС с синтезированными антеннами отдельные составляющие выходного эффекта оптимального фильтра, определяющими ЭПР измеряемого объекта, в соответствии с (26)–(45) при A 12 — A 21 — 0, равны:

11 — A21Sp,(54)

12 — A11A 22 Ic (^1,^2),(55)

15 — A11A22 Ic (^1,^2),(56)

I6 — A222Sp.(57)

Объединяя эти выражения, получим

с синтезированными антеннами, проведем путем сравнения с результатами, получаемыми ППС с реальными антеннами.

Во-вторых, с целью сокращения объема вычислений сравнение результатов измерений прове-

дем путем сравнительного анализа отдельных составляющих выходного этих систем (таблица)

Ввиду комплексного сопряженного характера составляющих выходного эффекта ППС с реаль-

ными и синтезированными антеннами, в которых имеются отличия, проведем сравнительный анализ выражений I 2 + I 5 + I 12 + I 15 :

– для ППС с реальными антеннами

• ⁵    В [1], частности, считается, что размеры антенн малы, расстояния, на которых проводятся измерения, по сравнению с размерами антенн и объекта велики и т. д.

• ⁶    К аналогичным результатам приводят приближенные вычисления с использованием разложения Френеля [2].

I 2 ⁺ I 5 ⁺ 1 12 ⁺ 1 15 ^{— 4(} A 11 A 22 ⁺ A 12 A 21 ) ^х х Re { I r (^ 2 ) I p (^,^ 2 ) } ;

7 Методом относительных измерений.

Таблица. Составляющие выходного эффекта измерительных систем с реальными и синтезированными антеннами Table. Components of the output effect of measuring systems with real and synthesized antennas

№ п/п	ППС с реальными антеннами	ППС с синтезированными антеннами
1	A U S r S p	A 21 S p
2	A ii A 22 I r ( 4 1 , 4 2 ) I p ( 4 1 , 4 2 )	A 11 A 22 I c ( 4 1 , 4 2 )
3	e 9 A 11 A 12 I p ( 4 1 , 4 2 )	e i 9 A 11 A 12 I p ( 4 1 , 4 2 )
4	e 9 A 12 A 1 I r ( 4 1 , 4 2 )	e 19 A 12 A 21 I p ( 4 1 , 4 2 )
5	A 11 A 22 X 4 1 , 4 2 ) I P ( 4 1 , 4 2 )	A 11 A 22 I c ‘ < 4 1 , 4 2 )
6	A2S r S p	A 22 S p
7	e i 9 A 22 A 12 M 4 1 , 4 2 )	e" i 9 A 22 A 12 I p ( 4 1 , 4 2 )
8	e A 22 A 21 1 ( 4 1 , 4 2 )	e 19 A 22 A 21 I p ( 4 1 , 4 2 )
9	e i 9 A„ A 12 I p ( 4 1 , 4 2 )	e i 9 A 12 A 11 1 } ( 4 1 , 4 2 )
10	e 19 A 22 A 12 I r ( 4 1 , 4 2 )	e i 9 A 12 A 22 I p ( 4 1 , 4 2 )
11	S r S p A 122	2 A 12 S p
12	A 12 A 21 I r ( 4 1 , 4 2 ) I p ( 4 1 , 4 2 )	A 12 A 21 S p
13	e ~ i 9 Au A 21 I r ( 4 1 , 4 2 )	e " i 9 A 21 Au I p ( 4 1 , 4 2 )
14	e" i 9 A 21 A 21 I p ( 4 1 , 4 2 )	e" i 9 A 21 A 22 I p ( 4 1 , 4 2 )
15	A 12 A 21 I r ( 4 1 , 4 2 ) I p ( 4 1 , 4 2 )	A 12 A 21 S p
16	S r S p A 21	2 a 21 S p

– для ППС с синтезированными антеннами

I 2 + I 5 + I 12 + I 15 = ^{( A} 11 A 22 + A 12 A 21 ) S p +

+ 2 A n A 22 + Re { I c <  4 1 , 4 2 ) } .

Если при анализе выражений (60) и (61) ограни- читься рассмотренным выше случаем малоразмерных антенн, то, как следует из выражения (54)– (58), при измерении ППС с реальными антеннами учитывается существующее на практике явление запаздывания передающего и принимаемого сигналов.

В то время как в ППС с синтезированными антеннами учитывается только запаздывание принимаемого сигнала, поскольку

Re { I c ( 4 1 , 4 2 ) } = cos 4 ^ [ R ( p , £1) - R ( p , £ 2 ) ] . (62) X

Кроме того, в выражениях (60) и (61) различным образом учитывается влияние интенсивности прямых и переотраженных сигналов. Поэтому измерение ЭПР сложных пространственно протяженных объектов (например, уголковых отражателей) ППС с синтезированием апертуры передающей и приемной антенн не обеспечивают.

В то же время, если уголковые отражатели имеют малые размеры и могут рассматриваться как точечные, ППС с синтезированными антеннами обеспечивают измерение их ЭПР.

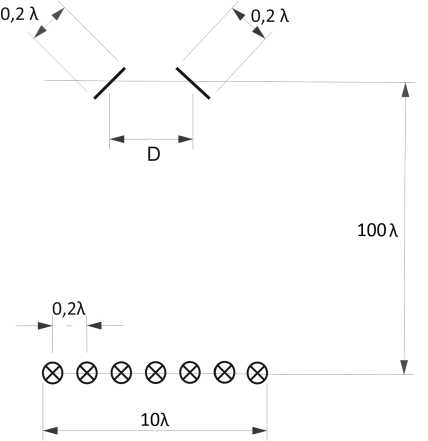
Рис. 1. Геометрия тестового объекта и схема размещения приемной и передающей антенн

Fig. 1. The geometry of the test object and the layout of the receiving and transmitting antennas

Результаты моделирования

Для подтверждения полученных результатов проведено математическое моделирование процесса измерения ЭПР тестового объекта. В качестве тестового выбран объект в виде двух электродинамически взаимодействующих изотропных идеально проводящих элементов (рис. 1). На рис. 2

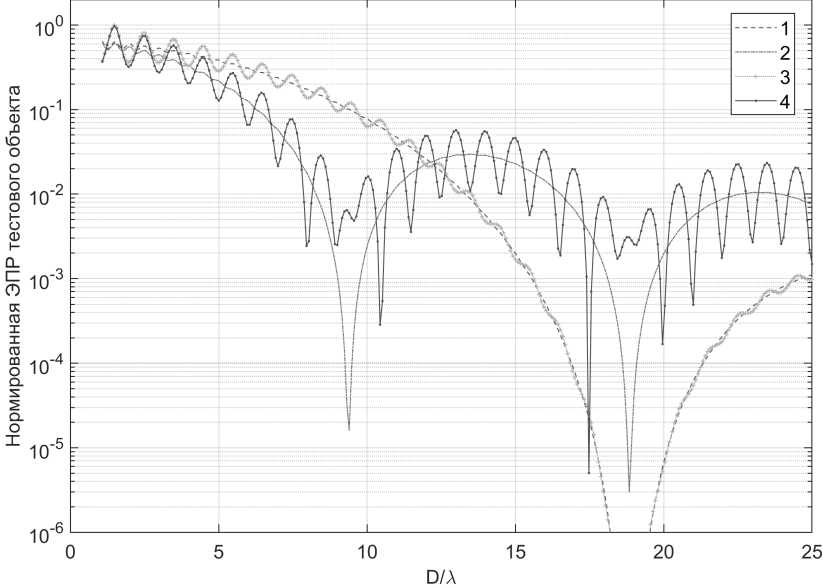
Рис. 2. Результаты моделирования измерения ЭПР пространственно-протяженного объекта: 1 – реальные антенны, элементы объекта электродинамически не взаимодействуют; 2 – реальные антенны, элементы объекта электродинамически взаимодействуют; 3 – синтезированные антенны, элементы объекта электродинамически не взаимодействуют; 4 – синтезированные антенны, элементы объекта электродинамически взаимодействуют

Fig. 2. The results of modeling the EPR measurement of a spatially extended object: 1 – real antennas, the elements of the object do not interact electrodynamically; 2 – real antennas, elements of the object interact electrodynamically; 3 – synthesized antennas, the elements of the object do not interact electrodynamically; 4 – synthesized antennas, the elements of the object interact electrodynamically

приведены результаты моделирования процесса измерения ЭПР для случаев взаимодействующих и невзаимодействующих элементов тестового объекта.

Заключение

Таким образом, достоверные результаты измерения ЭПР пространственно-протяженных объектов могут быть получены только при использовании реальных антенных систем. Использование для измерения ЭПР антенн с синтезированной апертурой накладывает ограничения на размеры и форму объектов измерения, а также приводит к необходимости коррекции алгоритмов обработки результатов измерений ЭПР в части учета систематических погрешностей, связанных с удвоением пространственной частоты отраженных сигналов.

Для «точечных» объектов результаты измерения ЭПР реальными и синтезированными антеннами сопоставимы. При измерениях пространственно протяженных объектов с электродинамически связанными элементами необходимо использовать измерительные антенны с реальными апертурами.