ИЗМЕРЕНИЕ СОСТАВЛЯЮЩИХ КОМПЛЕКСНОГО СОПРОТИВЛЕНИЯ ВЗАИМНОЙ ИНДУКЦИИ

Сопротивление взаимной индукции (ВИ) является одним из наиболее важных параметров электрических цепей, который необходимо определять для систем катушек, применяемых в различных областях, включая трансформаторы, электрические машины и аппараты, электромагнитные устройства автоматики и измерительной техники, технологии связи, производство и передачу электроэнергии. Помимо этих традиционных применений, появляются новые. Индуктивно-связанные катушки являются важными узлами систем беспроводной передачи энергии, которые уже нашли применение в бытовой электронике, промышленном производстве и медицинских имплантатах, активно изучаются возможности их применения для зарядки электромобилей. Другой развивающейся отраслью промышленности является робототехника. Здесь нужны системы точного измерения перемещений механизмов, способных работать в условиях загрязненных сред. Таким требованиям наилучшим образом удовлетворяют системы, по- строенные на базе датчика взаимной индуктивности. Широкое применение ВИ обуславливает требование постоянного совершенствования методов и средств измерения ее параметров.

МЕТОДЫ ИССЛЕДОВАНИЯ

В индуктивно связанных катушках сопротивление ВИ обычно определяется размером и геометрией обмоток, относительным положением между первичной и вторичной обмотками и витками обмоток. На частотах, превышающих f = 100 Гц, усиливаются эффекты "емкости" и "вихревых токов" [1–3]. Межвитковые емкости, потери на вихревые токи в проводниках обмоток, утечки и диэлектрические потери в изоляции приводят к ситуации, когда угол сдвига фазы между ЭДС E ₂ , индуцируемой во вторичной обмотке, и током I ₁ в первичной обмотке отличается от 90°. Нарушается также простая пропорциональность ЭДС E ₂ частоте и значению геометрической (низкочастотной) индуктивности M ₀ . Вместо идеального уравнения E ₂ = jroM ₀ 1 1 появляется зависимость

E ₂ =[ ст + jto ( M ₀ + AM ) ] I 1 = ( ст + jtoM ) I 1 , (1)

где σ и Δ M — корректирующие члены, называемые соответственно "примесью" и "частотной коррекцией" M 0 на частоте f . В комплексном сопротивлении ВИ Z M = ст + jtoM увеличивается эффективная взаимная индуктивность M = M 0 + A M , а малый угол 3 = = arctg ( ст/toM ) ® ст/toM отображает фазовый дефект ВИ.

Активное сопротивление σ зависит от частоты и некоторых других факторов. Наиболее подробно теория эффектов "емкости" и "вихревых токов" изложена в [1], теоретическая оценка дает приблизительно квадратичную зависимость σ от частоты f . Показано [1], что в случае, если первичная катушка должна пропускать большой ток, отклонение от квадратуры векторов E ₂ и I ₁ может стать значительным: рассмотрен пример, в котором даже при сравнительно низкой частоте f = 60 Гц дефект фазы составляет 75 мин. При применении ферромагнитных сердечников дефект фазы увеличивается и может достигать 10° [4].

В ряде случаев катушка ВИ используется для высокоточного установления сдвига фазы между током и напряжением на 90°, как, например, в прямоугольно-координатных потенциометрах, в стандартах высокочастотной мощности переменного тока и др. В [2] построена эквивалентная схема замещения катушек с индуктивной связью с учетом всех паразитных емкостей и получены математические зависимости σ и Δ M от этих емкостей. При разработке стандартов высокочастотной мощности необходимо очень точно знать фазовую погрешность шунтов переменного тока [5, 6]. Погрешность фазового угла сильноточных шунтов калибруется по шунту с известным фазовым углом. Сопротивления сильноточных шунтов обычно находятся на уровне МОм, а реактивное сопротивление шунтов, которое генерируется эквивалентной индуктивностью, является доминирующей частью на высокой частоте. Измерения дефекта фазы взаимной индуктивности на частотах от 20 кГц до 200 кГц произведены в [2].

Для инвариантного измерения составляющих комплексных сопротивлений широко применяются мосты переменного тока в режиме уравновешивания [7, 8]. Для уравновешивания моста две его составляющие должны быть регулируемыми и градуированными, обычно применяются переменные образцовые сопротивления или емкости [3, 9]. С применением моста UMPT-2 были измерены угловые погрешности катушек взаимной индуктивности типов KV-1 и KVI-5 ( M = 0.01 Гн и M = 0.001 Гн) в диапазоне частот от 400 до 2500 Гц [3].

Мосты переменного тока работают обычно на низких частотах — до 1000 Гц; при работе на повышенных частотах погрешность измерения резко возрастает [10]. Мостовые методы измерения имеют общий недостаток: в них не обеспечивается выходной сигнал с единственным информативным параметром для передачи на расстояние или сопряжения со средствами вычислительной техники с целью автоматизации процесса измерения и обработки результатов измерений.

СУЩНОСТЬ РАЗВИВАЕМОГО МЕТОДА ИЗМЕРЕНИЯ

Как показано в настоящем исследовании, указанный недостаток мостовых методов можно устранить, если использовать фазовый метод измерения составляющих Z_M [11]. Сущность метода поясняется с помощью рис. 1 .

В измерительной цепи (ИЦ) с первичной обмоткой ВИ последовательно соединены два образцовых резистора: опорный резистор R 1 и дополнительный резистор R 2 . В ИЦ измеряемые параметры σ и M преобразуются в угол фазового сдвига φ между выходными напряжениями u_S и u_N , которые поступают на аналоговые входы микроконтроллера (МК), при этом вторичная обмотка ВИ работает в режиме холостого хода.

В первом ( а ) и втором ( б ) положениях переключателя имеем соответственно

^U s 1 = I ( R 1 ⁺ ст + jtoM ) ,

US 2 = I ( R1 + R2 + ст + jtoM ), а опорное напряжение UN = IR1, где I — измерительный ток. Следовательно, будем иметь tg Ф1 = toM /(ст + Ri),                (2)

tg ф2 = toM(ст + R1 + R 2), преобразованием которых получаем to (ctg Ф2 - ctg Ф1)’

( R i + ^R 2 ) ctg Ф 1 ^- R i ctg Ф 2

ст =           ^:.                  (4)

ctg Ф 2 - ctg Ф 1

Видно, что обеспечивается независимое друг от друга (инвариантное) определение M и σ , при этом необходимо измерить только угол φ в двух положениях переключателя, а результат измерения не зависит от стабильности измерительного тока.

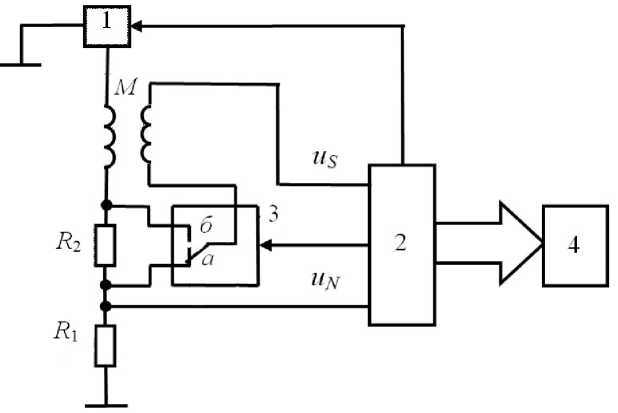
Рис. 1. Упрощенная функциональная схема измерителя.

1 — генератор синусоидального напряжения с программируемой частотой, 2 — микроконтроллер, 3 — электронный переключатель, 4 — цифровое табло

В экспериментальном образце измерителя использованы микросхема генератора AD9833 [12] и МК типа PIC32MX695F512H [13]. Аналоговые входы МК снабжены компараторами, где угол φ преобразуется во временной интервал τ , который измеряется в МК методом дискретного счета. При каждом измерении МК устанавливает требуемую частоту ω генератора, управляет положением переключателя, измеряет углы φ 1 и φ 2 , вычисляет значения M и σ по алгоритмам (3) и (4) и выводит результаты измерения на цифровое табло.

ВЫБОР ДИАПАЗОНА ШКАЛЫ И АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ

Анализ показывает, что из-за особенностей тангенсных и котангенсных функций чувствительность преобразования А ф = ф 1 - ф₂ максимальна в середине шкалы 0 ° <  ф <  90 ° угла и падает по краям этого диапазона, поэтому шкала угла ф выбрана в диапазоне 15 ° <  ф <  75 ° , что реализуется выбором сопротивлений R 1 и R 2 с учетом диапазонов измерения M и σ . При этом, поскольку Ф 1 > ф ₂, то верхний предел шкалы устанавливается значением сопротивления R ₁, а нижний — значением сопротивления R 2 .

Выполним расчет этих сопротивлений для случая частоты измерительного тока f = 1000 Гц и диапазонов измерения σ = 1–10 Ом, ωM = 100– 1000 Ом. Исключив из двух выражений (2) сумму (ст + R1), получаем

^R 2 = ^to ( ^M min • ctg Ф 2тп — ^M max ' ctg Ф 1тах ) •

С учетом значений ctg15 ° = 3.732 и ctg75 ° = = 0.268 получаем для шкалы M значение R ₂ - 105 Ом, а также ст + R 1 = 1000/3.732 -- 268 Ом, ст + R 1 + R 2 = 100/0.268 - 373 Ом. При этих значениях находим также углы ϕ _1min и ϕ _2max :

tg Ф 1т.п = ^M mn = ¹⁰⁰ - 0.373,    Ф 1„,п - 20.45 ° ;

ст + R1

tg ϕ ₂

= ® ^M max  = 1000 - 2.681,       = 69.55 ° .

max2max ст + R1 + R2373

По результатам расчета чувствительности преобразования на рис. 2 построена кривая зависимости А ф = f ( ф ) .

Для выбора шкалы σ следует учесть, что с увеличением σ угол φ уменьшается, как видно из (2). Поэтому целесообразно измерить вместо σ добротность вторичной обмотки ВИ Q = toM/ст , поскольку, имея значения ωM и Q , МК вычислит значения σ .

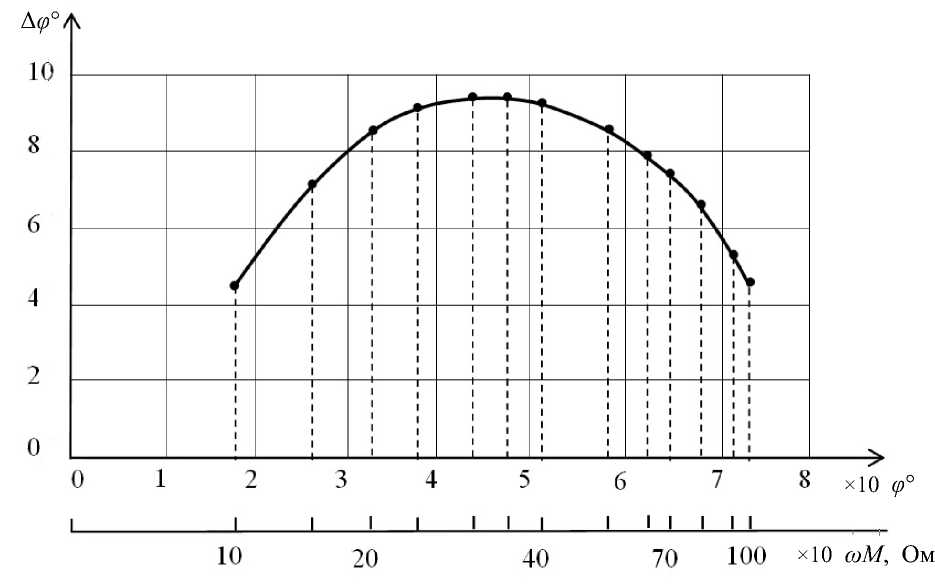
Рис. 2. График зависимости чувствительности преобразования А ф = f ( ф ) вдоль шкалы угла ф

Из (3) и (4) следует, что

tg Ф 2min =

Q = 7--------. R'-------------,

( R i + R ₂ ) ctg ф 1 - R , ctg Ф 2

Q min

^Q max/ tg Ф 1max ^{+ R} 2/ ° ’

а диапазон измерения Q , определяемый диапазонами измерения ωM и σ , будет Q = 100–1000. Представим формулы (2) в виде:

tg ϕ ₁

Q

1 + R 1 о ’

откуда находим отношение

^R 2/ ° = Q min/ tg Ф 2min ^{- Q} max/ tg Ф 1тах » ¹⁰⁵

Следовательно, о = R 2 /105 = 1.0 для всей шкалы, с учетом чего из (8) находим R 1 = 267 Ом. Таким образом, для M и Q получаем единую шкалу угла φ .

tg Ф 2 =

Q

1 + ( R i + R 2 ) о

Для шкалы Q целесообразно сохранить значение сопротивления R ₂ = 105 Ом, которым устанавливается чувствительность преобразования. Для отметки ϕ _1max шкалы из (6) определяем

^{1 +} R 1 ° = ^Q max/ tg Ф 1max             ⁽⁸⁾

и подставляем в формулу (7), представленную для начальной отметки шкалы:

ИССЛЕДОВАНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ

Произведена теоретическая оценка погрешностей определения M и Q по формулам (3) и (5). Нестабильность частоты ω не вызывает погрешности в (3), поскольку при вычислении угла φ по формуле ф = (т/ T ) • 360 ° МК измеряет также период T = 1] f измерительного тока. Поэтому относительная погрешность определения M будет

Y ( M ) _

A M _ A R 2 + A ( ctg ф ₁ ) -A ( ctg Ф 2 ) M R 2       ctg Ф 2 - ctg Ф 1

_ Yr ( M ) + Yф (M ),( где обозначены частные погрешности:

Yr (M) = AR2/R2 _ y(R2),(10)

Y (M)_ A(ctgФ1)-A(ctgФ2) _ ф            ctg Ф2 - ctg Ф1

_ ctgФ1 - Y(ctgФ1)-ctgФ2 - Y(ctgФ2)

ctg Ф2 - ctg Ф1

Аналогичным образом получаем из выражения (5):

Y ( Q ) ^_ Y r ( Q ) ⁺ Y ф ( Q ) ,

A_r ( Q)

Y r ( Q ) _ "Q^

_ ^R i ( ctg Ф 2 ^-ctg Ф 1 ) ^[ Y ( ^R i ) ^- Y ( ^R 2 ) ]

( R + R 2 ) ctg Ф 1 - R i ctg Ф 2      ,

Y ф ( Q 1^ _

_ R _L• ctg ^ф 2; ^Y (ctg ^ф 2) - ( R ^+ R 2) ctgf ; • ^Y (ctg ^ф 1) ( R + R 2 ) ctg ф 1 - R i ctg Ф 2

Анализ показывает, что фазовый метод измерения параметров ВИ чрезмерно критичен к стабильности сопротивлений резисторов R1 и R2 , поэтому выбраны наиболее высокоточные металлофольговые резисторы типа С5-61 [14]. С учетом значений допуска ±0.005% от номинального сопротивления RN и ТКС at _ ±10 -106 °C1 абсолютное изменение сопротивления резистора в нормальных условиях эксплуатации (при температуре 20 ± 5 °C) будет

ARx _ 0.00005R, +ARt -±1.5-10-4 R,, где ARt _at -At- R, _ 10-10-6 -10R, _±10-4R, — температурное изменение сопротивления резистора. Следовательно, частная относительная погрешность измерения M от изменения сопротивления резистора R2 с учетом (10) будет

Y r ( M ) _ Y ( R ) _A R _z/ R_w _ 1.5 - 10 - 4 .

Можно считать, что погрешности резисторов R 1 и R ₂ являются некоррелированными случайными величинами с нормальными законами распределения, поэтому для среднеквадратических отклонений о [ y ( R ) ] их сопротивлений можно принять с доверительной вероятностью 0.95 [15]

^{о [} Y ( ^R 1 ) ] ^{_ 0 [} Y ( ^R 2 ) ] ^{_ 0} [ Y ( ^R ) ] ^_ 0.^{5A R} x ^_

_ 0.75-10-4, с учетом чего получаем

^{0 [} Y ^{( R} 1 ^)- Y ^{( R} 2 ) ] ^_ V^{2 0 2 [} Y ^{( R} ) ] ^_

_ 1.41 o [ y ( R ) ]_ 1.41 - 0.75 - 10 - 4 » 1.06 - 10 - 4 .

Подставляя в (12)

[ Y ( R 1 ) - Y ( R 2 ) ]_ 2 - о [ Y ( R 1 ) - Y ( R 2 ) ]* 2.1 - 10 - ⁴

и значения сопротивлений R 1 и R 2 , получаем

_ 2.1 - 10 - ⁴ - ( ctg Ф 2 - ctg Ф 1 )

• 1.4 - ctg Ф 1 - ctg Ф 2

В табл. 1 представлены результаты расчета

Y _r ( Q ) по формуле (14), где принято обозначение A _ ctg Ф 2 - ctg Ф 1 .

Табл. 1. Расчетные значения погрешности y _r ( Q ) при R ₁ _ 267 Ом, R 2 _ 105 Ом

Функция	Q
	100	200	300	400	500	600	700	800	900	1000
ctg ϕ 1	2.680	1.340	0.893	0.670	0.536	0.446	0.383	0.335	0.298	0.268
ctg ϕ 2	3.730	1.865	1.243	0.933	0.746	0.621	0.533	0.466	0.415	0.373
A	1.050	0.525	0.350	0.263	0.210	0.175	0.150	0.131	0.117	0.105
Y r ( Q ) , %	1.00	1.002	1.021	1.105	1.002	1.081	0.984	0.917	1.112	1.002

Расчеты показывают, что частная погрешность определения Q от изменения сопротивлений резисторов R 1 и R 2 с доверительной вероятностью 0.95 не превышает значения y R ( Q ) — 1.2%. Для уменьшения этой погрешности можно перед монтажом резисторов определить точные значения их сопротивлений.

Частные погрешности уф (M) по формуле (11) и Уф (Q) по формуле (13) зависят от точности измерения фазовых углов φ1 и φ2. Относительная погрешность измерения фазового сдвига φ имеет две составляющие: погрешность у(т) преобразования угла φ во временной интервал τ и погрешность у (ф) — фф/ф измерения длительности импульсного сигнала — у Д Ф ) = Y (т) + Y (ф ). Погрешность у (т) зависит от напряжений смещения нуля входных компараторов МК; практически ее можно устранить, используя способ биполярного измерения, при котором τ определяется по четырем моментам перехода через нулевые значения синусоиды в обоих направлениях (в течение одного периода входного напряжения получаются два временных интервала т) [16]. Следовательно, относительная погрешность определения ctgϕ будет зависеть только от точности измерения фазового сдвига φ и может быть вычислена по выражению у (ctg ф , '" ctg ф) — J.д^5t8Фl ,фф = ctg ф ctg ф   дф

Ф      Аф _ 2ф- Y ( ф )

—--I--- • ----- —--.

ctg ф • sin2 ф ф      sin 2ф или

7 ^в 1 ² • Y ² ( ф ) • ctg² ф ^{+ в} 22 • Y ² ( ф 2 ) • ctg² ф 2~

ctg ф 2 - ctg ф

Т.к. углы φ 1 и φ 2 измеряются одними и теми же аппаратными средствами практически одновременно, то можно принять, что у ( ф 1 ) ~ ~ Y ( ф ₂ ) — Y ( ф ) , следовательно,

( , , X   Y ( ф ) 7 ^в 1 • ctg ф ^{+ в} 2 • ctg ф 2

Yф(M)—     —;-----;--------- ctg ф2 - ctg ф1

С учетом выражения β получаем:

Y ф ⁽ M ^{) —}

0.0175 • y ( ф ) ctg ф 2 - ctg ф 1 ^|

ф ^ I _v sin² ф 1 J

_Ф^_

^ Sin ф ₂

Произведя аналогичные действия с выражением (13), получаем:

Y ф ⁽ Q ^{) —}

X

Y ( ctg ф ) —

2пф^у ( ф ) 180 • sin2 ф

0.035 ф ^ у ( ф ) sin 2 ϕ

— в • Y ( ф ) ,

0.035 ϕ где в —--, а угол ф выражен в радианах.

sin 2 ϕ

Следовательно,

Y ( ^ctg ф ) ^— А • Y ( ф ) , Y ( ^ctg ф 2 ) ^{— в} 2 • Y ( ф 2 ) .

Погрешности у ( ctg ф 1 ) и у ( ctg ф ₂ ) являются случайными и независимыми, поэтому с доверительной вероятностью 0.95 можно принять, что Y ⁽ ctg ф ^{) —} 2 ^ ( ctg ф , ) , Y ⁽ ctg ф 2 ^{) —} 2 ^ ( ctg ф 2 ) , ^следо^вательно, c учетом выражения (11) получаем:

Y ф ⁽ M ^{) —}

0.0175 • y ( ф )

( 1⁺ R 2/ R 1 ) ^ctg ф 1 ^{- c}tg ф 2

ф 2

_v sin² ф ₂

I + ( 1 + R 2 /R 1 ) 2 •

_фк_ I v sin2 ф1 J

.

Для вычисления погрешностей по выражениям (15) и (16) необходимо найти значение у (ф). Измерение фазового сдвига φ выполняется в МК по формуле ф — (т/T)• 360° путем заполнения временных интервалов т и T импульсами образцовой частоты f, — 80 МГц тактового генератора. Показание таймер-счетчика будет ф — nf^ • 360° — n • 360°, Nf0       N где n и N — количества импульсов, поступивших на таймер-счетчик за время τ и T соответственно.

Абсолютная погрешность измерения угла φ будет

. дф . дф . (Аn n .

Аф — -Аn +—AN —----AN 360°, дп dN In N2 J

а относительная погрешность:

у (ф) —Аф ϕ

A n NJ

—

.

nN

Табл. 2. Расчетные значения погрешности Y _ф ( M ) при R 1 = 267 Ом, R 2 = 105 Ом, f = 1.0 кГц, f₎ = 80 МГц

Функция	ωM , Ом
	100	200	300	400	500	600	700	800	900	1000
A	1.050	0.525	0.350	0.263	0.210	0.175	0.150	0.131	0.117	0.105
φ 1 , град.	20.455	36.723	48.214	56.168	61.800	65.923	69.043	71.473	73.412	75.000
φ 2 , град.	15.000	28.191	38.799	46.990	53.267	58.123	61.940	64.995	67.481	69.538
B	4.878	2.857	2.293	2.090	2.004	1.970	1.958	1.959	1.962	1.969
Y ( ф ) - 105	31.250	17.238	12.848	10.827	9.698	8.992	8.515	8.174	7.919	7.721
Y ф ( M ) - 10 3 %	2.547	1.642	1.473	1.506	1.620	1.772	1.945	2.136	2.324	2.534

Погрешность у ( ф ) определяется случайной погрешностью дискретности, т.е. возможностью потери в числах n и N по одному счетному импульсу. Наихудший случай имеет место, когда A n = 1, AN = - 1:

1  1 Г Т ,11

y ( ф ) = ¹ +± = Ts- + A- = T I ¹ + A n N nT₀ NT₀   ⁰ ( т T

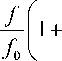
360 °

ϕ

При имеющихся значениях J = 1.0 кГц, f ₀ = 80 МГц получаем

Y ( ф ) = ± 1.25 - 10 ^{- 5} -I 1 + 36⁰- L

I Ф )

В табл. 2 представлены результаты расчета погрешности Y_ф ( M ) , вычисленные по формулам (15) и (17), где приняты обозначения

Аналогичный расчет по формулам (16) и (17) погрешности Y_ф ( Q ) показал, что она также минимальна в середине шкалы, где Y_ф ( Q ) ~ 0.57% при ф = 45 ° , и принимает максимальное значение Y_ф ( Q ) = 1.16% в начале шкалы при Q = 100. Видно, что Y_ф ( Q ) существенно больше Y_ф ( M ) •

Частные погрешности Y r ( ^M ) ^и Y ф ( ^M ) , Y R ( Q ) и Y_ф ( Q ) случайны и независимы, поэтому пределы допускаемых полных основных относительных погрешностей определения M и Q с доверительной вероятностью 0.95 будут

Y (M) = J[Yr (M )]2 +[Yф (M)]2 =

= 10 ^{- 4} - V 1.5² + 0.255 2 » 0.016%,

Y(Q) = V[Yr (Q)]2 +[Yф(Q)]2 =

= 10 ^{- 2} - V 1.2 2 + 1.16² » 1.67%

A = ctgФ2 -ctgфх, соответственно, с учетом соотношения <г = aM/Q

B =

Ф 1

\ I sin² Ф 1

+

Ф 2

_v sin² ф₂

получаем

Y (^) = V[ Y (M)] 2 +[ Y (Q)] 2 =

а в формуле (17) подставлены значения ф = ф ₂, поскольку всегда ф ₂ <  ф 1 , а нас интересует предел допускаемой погрешности измерения. Из табл. 2 видно, что погрешность Y_ф ( M ) минимальна в средней части шкалы угла ф , при ф = 45 ° Y_ф ( M ) » 1.46 - 10 - ³% , и увеличивается по краям шкалы. Максимальное значение этой погрешности равно 2.547 - 10 ^{- 3}% .

= V 0.016² + 1.67² » 1.68%.

ВЫВОДЫ

В фазовом методе не используются аналоговые сигналы. Во многом благодаря этому метод позволяет сравнительно просто автоматизировать процесс измерения, реализовать инвариантное цифровое измерение активной и реактивной составляющих комплексного сопротивления ВИ магнитно- связанных катушек и обеспечить достаточную для практики точность. Результаты исследования показывают, что в разработанном микроконтроллерном устройстве погрешности определения активного сопротивления σ и индуктивности M комплексного сопротивления ВИ можно обеспечить не более у(^) = 1.68% и Y (M) = 0.016% с доверительной вероятностью 0.95. При этом можно уменьшить погрешности измерения сужением по краям шкалы угла φ.