Изотермическое течение Куэтта–Пуазейля вязкой несжимаемой жидкости с малой вертикальной скоростью

Точные решения уравнений гидродинамики используются для математического моделирования многих процессов химической и нефтехимической технологий, включая процессы конвективного массо- и теплопереноса и различных природных явлений [1–4]. Адвективные изотермические течения невращающейся вязкой жидкости исследовались многими авторами [5–9]. В работах [1, 2, 5–9] рассматривалось применение класса точных решений уравнений Навье–Стокса для сжимаемой жидкости с линейной зависимостью компонент решения от двух координат. Коэффициенты линейных функций зависят от третьей координаты. Решение задачи сводится к интегрированию нелинейной системы обыкновенных дифференциальных уравнений. В научных статьях [10–14] предлагается использовать этот класс точных решений для описания адвективного (слоистого) течения вязкой несжимаемой жидкости. В результате подстановки класса решений в уравнения Навье–Стокса получается переопределенная система обыкновенных дифференциальных уравнений. Однако, как замечают сами авторы, вопрос об условиях совместности полученной системы обыкновенных дифференциальных уравнений ими не рассматривался.

В работах [15–18] построены точные решения системы уравнений Навье–Стокса с линейной зависимостью горизонтальных компонент скорости от двух координат, описывающие адвективное (слоистое) течение вязкой несжимаемой жидкости. Такое решение будем называть неоднородным, в отличие от точного решения, в котором компоненты скорости зависят только от одной координаты. В работах получены и исследованы условия совместности системы уравнений, описывающей неоднородное решение. Условия совместности накладывают некоторые ограничения на компоненты скорости течения жидкости и, следовательно, на граничные условия задачи.

В настоящей работе исследуется неоднородное решение, описывающее изотермическое течение вязкой несжимаемой жидкости по твердой плоскости с учетом скольжения по твердой по- верхности при малых нарушениях условий совместности. Предполагается, что отклонения пропорциональны малому параметру. Решение построено в виде ряда по степеням малого параметра. Коэффициенты рядов являются многочленами вертикальной переменной. Построены первые приближения решения. Показано, что при нарушении условий совместности возникает вертикальная компонента скорости.

Постановка задачи

Рассмотрим установившееся изотермическое движение вязкой несжимаемой жидкости в бесконечном горизонтальном слое жидкости. Течение описывается уравнениями Навье–Стокса, которые в безразмерных переменных имеют вид:

д V   д V   д V    д P  1

Vx —- + VУ —x + Vz —x =--+ — A Vx, дx   y ду     дz    дx  Re д Vv    д Vv    д Vv др 1

Vx — + V — + Vz — = —— + — AVy, дx   y ду     дz    ду  Re y дV    дV    дVz

—

1 д P 1

—т---+--A V _z ,

8² д z  Re

Vx —- + V —z + Vz —z = дx   y дУ      дz д Vx  д Vy  д V o

+    +    = 0

д x    д у    д z

В системы (1) введены следующие обозначения: Vx, Vy, Vz - безразмерные компоненты вектора скорости жидкости; Vh - характерный масштаб горизонтальных компонент скорости; масштаб вертикальной компоненты скорости выбран в виде Vv = 8Vh; безразмерные горизонтальные координаты x, у определены характерным масштабом длины L, а поперечная координата z - толщиной слоя жидкости h; 8 = h/L - отношение масштабов длины, v - коэффициент кинематической z                                                                                         .    д2    д2     1 д2

–

(молекулярной) вязкости жидкости, Re = LV_h V - число Рейнольдса, А = —_?+--г + — —- д x ²   д У 2   8 2 д z ²

оператор Лапласа в безразмерных переменных.

Для нахождения частного решения системы уравнений (1) зададим граничные условия на обеих границах слоя жидкости. На нижней, твердой поверхности, описываемой уравнением z = 0, предполагается скольжение жидкости согласно условию Навье [19-24]:

( 1 д Vx  sd V a I--x + 8 —z

{ 8 дz     дx

= Vx, a z=0

1 д V_{y   s} d V

--^— + 8 —^z

8 д z      д у

z = 0

y

и условие непротекания V_z | = 0. Здесь a - безразмерный коэффициент трения. На свободной недеформируемой поверхности (приближение «твердой» крышки), описываемой уравнением z = 1, задана сила F в безразмерном виде с компонентами F = ( t_x , т _у , P a ) . Компоненты силы T _x , т - задают касательные напряжения на свободной поверхности жидкости, моделирующие воздействие ветра [19-24]:

1 д V_x   ? d V_z

--- + 8 —^z

8 д z      д x

= ^T x , z = 1

1 д V_{y   s} d V_z

--^— + 8 —^z

8 дz     д-у

ту • z=1

Будем считать, что касательные напряжения Tx , ту являются линейными функциями гори зонтальных координат:

^T x = ^т 10 ^{+ x T} 11 ⁺ У ^т 12 , ^т у = ^т 20 ^{+ x T} 21 ⁺ У ^т 22 , где T ij - постоянные. Третья компонента силы F - давление атмосферы P _а . Давление P _a задается квадратичной функцией:

^P a = P 0 ^{+ x}P 10 ^{+ yP} 01 ^{+ x P} 20 ^{+ xyP} 11 ^{+ у} P 02 , где P 0⁰ , P 0 , P 001 , P 0 , P 10 , P 02 - постоянные.

Механика

Точное решение системы (1) будем искать в полиномиальном классе Линя–Сидорова– Аристова [1, 3]

V x = U 0 ( z ) + ^xU 1 ( z ) + yU 2 ( z ) , V y = V 0 ( z ) + ^xV 1 ( z ) + yV 2 ( z ) ,

V z = w ( z ) ,                                            (4)

P = P 0 ( z ) + x^P 10 ( z ) + yP 01 ( z ) + x ² P 20 ( z ) + xyP ll ( ^z ) + y ² P 02 ( ^z ) .

Здесь U ₀ , V – фоновые слагаемые горизонтальных компонент скорости жидкости, функции U ,

V ₁ , U ₂ , V ₂ описывают скорость деформации элемента жидкости (пространственные ускорения).

После подстановки вида решений (4) в систему исходных уравнений (1) получим систему обыкновенных нелинейных дифференциальных уравнений:

U 0 = J ² Re [ P o + U 0 U 1 + V o U 2 + WU 0 ] , V = J ² Re [ P 01 + U 0 V 1 + V 0 V 2 + WV 0 ] ,

U ‘ = Re J ² ( 2 P ₂₀ + U 1 2 + U₂V 1 + WU ’ ) , U 2 = Re J ² ( P 11 + U 1 U 2 + U₂V₂ + WU 2 ) ,

V = J ² Re ( P 1 + U 1 V 1 + VV 2 + WV 1 ' ) , V 2 = J ² Re [ 2 P 02 + U 2 V + V ² + WV 2 ] ,         (5)

W" = Re P ₀₀ ' + Re J ² WW , U 1 + V ₂ + W' = 0,

P 0 = 0, P 1 = 0, P 20 = 0, P 02 = 0, P 1 = 0.

Здесь и далее штрихом обозначается производная соответствующей функции по переменной z.

Для слоистого течения ( W ( z ) = 0) система уравнений (5) примет вид:

U 0 = J ² Re [ P 0 + U 0 U 1 + V)U 2 ] , V 0 = J² Re [ P ₀ 1 + UV + V₀V₂ ] ,

P00 = 0 , P10 = 0 , P01 = 0 , P20 = 0, P02 = 0, P11 = 0 ,

U ’ = Re J ² ( 2 P 20 + U 2 + U 2 V ) , U 2 = Re J ² ( P 1 + UU 2 + UV ) ,

V= J2Re (P1 + U1V1 + VV2 ), V"J2Re [2 P02 + U2V + V ],(7)

U1 + V2 = 0.(8)

Граничные условия (2) и (3) для систем уравнений (6)–(8) с учетом класса решения (4) следую-

Щ                            J U 0 ( 0 ) = aU 0 ( 0 ) , S V ( 0 ) = aV ( 0 ) ,

JU1 (0) = aU;(0), JV1 (0) = aV1'(0), JU2 (0) = aU2 (0), JV2 (0) = aV2(0),(9)

U 0 ( 1 ) = Jt_w , V ( 1 ) = Jt 20 , U ; ( 1 ) = JT 11 , V ^;( 1 ) = Jt 21 , U 2 ( 1 ) = J7 _n, V 2 ( 1 ) = Jt 22 ,

P 0 ^{( 1 )} = P 0 , P 01 ^{( 1 )} = P 01 , ^P 20 ^{( 1 )} = ^P 20 , ^P 02 ^{( 1 )} = ^P 02 , ^P 11 ^{( 1 )} = ^P 11^.

Система (6) описывает фоновые слагаемые компонент скорости, а система уравнений (7), (8) – коэффициенты сдвиговых слагаемых компонент скорости жидкости. Система нелинейных обыкновенных дифференциальных уравнений (7), (8) – переопределенная (дифференциально алгебраическая) система уравнений. Условия совместности системы (7), (8) исследовались в работах [1, 2, 15] и имеют вид

U1+U2V1 = 0,(10)

P20 = 0, P02 = 0, P1 = 0.(11)

Общее решение системы (7) с учетом условий совместности (10), (11) и условия несжимаемости (8) представляется линейными функциями переменной z :

U 1 = C 1 z + C₂ , U ₂ = C 3 z + C 4 , V 1 = C ₅ z + C 6 , V ₂ =- ( C 1 z + C 2 ) .

Условие совместности (10) в терминах граничных условий (9) получится следующим [6]: t12t21 + T21 = 0,

P20 = 0, P101 = 0, P002 = 0, а условие несжимаемости (8)

т„ + T 22 = 0 .                                        (13)

При выполнении условий совместности (12) реализуется слоистое изотермическое течение вязкой несжимаемой жидкости.

Рассмотрим решение системы (5) при малых нарушениях (возмущениях) условия совместности. Для этого представим касательные напряжения на свободной границе в виде т11 = т11 + ^т11 , т12 = т12 + ^T12 ’ т21 = т21 + ^T21 , T22 = -т11 + ^T22 ’ где и - малый параметр, т^ - невозмущенные значения, т1 - возмущения касательных напряжений. Соответственно, коэффициенты квадратичных слагаемых в выражении давления атмосферы 010101

P 20 = M P 20 , P 11 = M P 1 1 , P 02 = ^ P 02 .

Слагаемые касательных напряжений на свободной поверхности т ₁₀ , т ₂₀ и коэффициенты линейных по x , у слагаемых давления не входят в условия совместности и считаются невозмущенными. Считается, что при н = 0 выполняются условия совместности (12) и условия несжимаемости (13) и невозмущенное движение является слоистым:

( т ⁰, ) ² + тт 1 = 0.

Тогда выражение (12) с подстановкой возмущений примет вид о_1 .-о _1 ,01 _ О 1 V 2 (( 1 \2, 11 Ln Н(т11т11 + т12т21 + т21т12 т11т22) + н 1(т11) + т12т21 1 = 0 .

Для удобства дальнейших исследований представим решение исходной системы уравнений ( ) V'^U 0 + X ( б ( z ) + „ ( . •) ) + y ( / 2 ( z ' ) -O ( z •) ) , V y = V 0 ( z■ ) + x ( Y 2 ( Z W Z ) ) + y ( б ( Z ) - Y 1 ( z■ ) ) ,

V z = w ( z ) ,                                         (14)

^P = P 0 ( ^z ) ^{+ xP} 10 ( ^z ) ⁺ y^P 01 ( ^z ) ^{+ X 2} P 20 ( ^z ) ⁺ xyPH ( ^z ) ⁺ У ² P 02 ( ^z ) .

Переменная £ = ( U 1 + V ₂)/2 описывает скорость изменения площади элемента жидкости, Q = ( V — U 2 )/2 — угловую скорость вращения элемента жидкости, / 1 = ( U 1 - V₂ )/2, Y 2 = ( U 2 + V )/2 — компоненты девиатора тензора скоростей деформаций элемента жидкости.

При подстановке класса решения (14) в систему уравнений (1) получим следующую систему обыкновенных нелинейных дифференциальных уравнений:

U 0 = 8 ² Re [ P 0 + U 0 £ + Y 1 ) + V 0 ( / 2 -Q ) + WU 0 ] ,

V 0 = 8 ² Re [ P 01 ( z ) + U 0 ( z ) ( Y 2 ( z ) +□ ( z ) ) + V ( z ) ( б ( z )-_n ( z ) ) + W ( z ) V J ( z ) ] ,

W " = Re ( P + 8 WW ') , Q" = Re 8 ² ( 2 £ ^+ W Q' ) , £ + W ' = 0,

_Z [ = Re 8 ² ( P 20 - P 02 + 2 6/ 1 + W y' ) ,                           (15)

Y 2 = 8 ² Re ( P 11 +2 sy 2 +W y'2 ) ,

P 0 = 0, P 10 = 0, P 01 = 0, P 20 = 0, P )2 = 0, P = 0,

6" = Re ^ ² ( P ₂₀ + P ₀₂ + £ ² + Y 1² + Y 2 -Q ² + W £ ') .

Граничные условия (2), (3), в соответствии с видом решения (14), получатся следующие: на нижней границе жидкости:

S U 0 ( 0 ) = aU 0 ( 0 ) , Y ( 0 ) = a Y 1 ( 0 ) , Y ( 0 ) = a Y 2 ( 0 ) , V 0 ) = aV 0 ( 0 ) , 8 Q' ( 0 ) = a Q ( 0 ) ,

8£ ' ( 0 ) = a £ ( 0 ) , W ( 0 ) = 0;

на свободной поверхности:

U 0 ( 1 ) = 8т_ю , V 0 ( 1 ) = 8т 20 , 6 ( 1 ) = ^8 ( т 11 + т 22 ) /2, y ' ( 1 ) = 8т_п ,

Y 2 ( 1 ) = 8 ( T 12 + т 21 )/2, Q ( 1 ) = 8 ( т 21 - T 12 )/ 2,                          (16)

Механика

P 20 ( 1 ) - ^P 20 P 02 ^{( 1 ) -} P 02 , P 11 ^{( 1 ) -} P 1 •

Выделим два случая возмущений. Первый - возмущения касательных напряжений T ij на свободной поверхности. Возмущения T ij могут не удовлетворять условиям совместности (12) и условию несжимаемости для слоистого течения (13). При этом будем считать, что давление P ⁰ ( x , у ) на свободной поверхности невозмущенное и описывается линейной функцией горизонтальных координат согласно условию совместности (11). Второй случай - касательные напряжения на свободной поверхности невозмущенные, T j - 0, а давление представлено квадратичной функцией горизонтальных координат (14), коэффициенты при квадратичных слагаемых пропорциональны малому параметру р •

Построение решений для возмущенных касательных напряжений

Первый случай. На свободной поверхности возмущенные граничные условия зависят от малого параметра р и имеют вид (16). Решение системы уравнений (15) при граничных условиях (16) ищем в виде рядов по степеням малого параметра р:

да                                         да                                        ад

U 0 ( z , и ) - Х и m U 0 m ( z ) , V 0 ( z , и ) - Х и V ( -■ ) . W ( - ', и ) - Х и m W m ( z ) .

m -0                        m-0

дада

№ ( z , ц ) - Х и ^m £ ^m ( z ) . H ( z , ц ) - Х И ^m H ^m ( z ) .

m-0

дада

/1(z.и)- ХиY(z).  Y (z,и)- Хиmr2”(z)• m-0

Так как невозмущенное течение слоистое, то № (z)- 0 и W0 (z)- 0. Приравнивая коэффициен ты при одинаковых степенях малого параметра ц, получим последовательность неоднородных систем линейных обыкновенных дифференциальных уравнений. Система уравнений m-ого приближения имеет вид:

i + j - m ,                                                   _x

U m "- 6 ² Re

P1 m + Х (U0(№ + Y1)+Vi(rj-hj)+WJU0")

i , j - 0

Vm" - 6 ² Re

Pm + (Vi №j — Yij) — U0 (rj + Hj) + WJV0")

i + j - m

W ^m "

- Re P₀ ^m " + 6 ² Х WW^j "

0               i ^, j ^{- 0}

Hm" (z) - Re 62 i +Хm (2?Qj + WiHj'). i, j-0 V m2

/ 1   - Re 6

( i+j - m /

Х IW+ W i i , j - 0 0

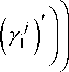
pm _ pm , ^P20  P 02 ⁺

I

(       i+j -m( m2

/ 2 - 6 Re

pm + Х12p?j+Wi (/j)

<         i ^, j ^{- 0 0}

mmmmmm

^P 0   ^{- 0} . ^P 10 ^{- 0} . ^P 01 ^{- 0} . ^P 20 ^{- 0} . ^P 02 ^{- 0} . ^P 11 ^{- 0} .

m 2

№  - Re 6

P0 + P2 + Х Pp +rY + r2rj-aH’ +wV) i, j-0X

Система уравнений при нулевой степени параметра ^ называется порождающей. Порождающая система описывает адвективное течение несжимаемой жидкости и является переопреде- ленной или дифференциально-алгебраической. Одно из уравнений системы - алгебраическое соотношение. При выполнении условий совместности (11), (12) и условия несжимаемости (13) для слоистого течения порождающая система примет вид:

0     2      0    00    0  0    0      0     2      0    00    0  00

Uо = 8 ReL^1о + UоY1 + Vo (Y2 -^ U, Vo = 8 Re|_^01 -Vo Y1 + Uо (Y2 + q )J о”"- о, /0' = 0, у’- 0,(19)

Ро + P)2 +(Y10 )2 +(Y0 )2 — (Q )2 = 0.(20)

Условие совместности (12) в новых переменных преобразовалось в алгебраическое соотношение (20), связывающее переменные, описывающие компоненты скорости сдвига у ^ , у ⁰ , угловую скорость вращения элемента жидкости Q ⁰ и коэффициенты давления Р ₂ ⁰ ₀ , Р О’ , р ⁰ [3, 4]. Общее решение системы (19) с учетом невозмущенных граничных условий имеет вид:

Y 1⁰ ( z ) = С 1⁰ ( z + a / 8 ) , у ⁰ ( z ) = C 3 ( z + a / 8 ) , Q ⁰ ( z ) = C ⁰ ( z + a / 8 ) .

0    24   0   0  0   00

U 0 = Re ⁸ ( ( ^C 3 ^{- C} 5 ) ^P 01 ^{+ C} 1 ^Р 10 )

z ⁵    z ⁴ I a 1

40  241812

+ z

a2   5 a   5

--у +----1+

82  6 824

3     2   3     22

a    5 a z a z a 5 a

+-- Z-- +-- Z-------Z-- 1---

8³    5 8 ²    3 8  2 8 ²   24 8

I        a ) о

+ 1 z + 7P k     8 J

+ Re P 10 8 ²

I z 2

a

— z--

⁸ J

+

00     0    0  0   2

+ ^Re ( ^C 1 r _w + ( ^C 3 ^{— C} 5 ) ^T 20 ) ⁸

4   3    22

z za za

--1----1---у

12   3 8  2 8 ²

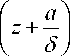
a ²

a 1

V ’ ( z ) = Re ² 8 ⁴

0   0    0  0    00

^C 1 ^{( ( C} 3   ^C 5 ) ^P 01 ^{+ C} 1 ^P 10 ) z ² a ² z³ a  z ⁵    z ⁴ I 1 a P

+ 1

C ₃ ⁰ — C ₅ ⁰          [ 2 8 ²    3 8  40  12 I 2 8 J

—

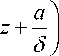
У 2

a 10 a 5

_k 8 2 + 12 8 ⁺ 24

( -2        „)

+ т ’о I z + a | + Re P _o0 8 ²-- z — a + ²⁰ 1    8 J       ⁰¹    ^ 2        8 J

+ Re

0   00     0    0  0

^C 1 ( ^C 1 ^T 10 ⁺ ( ^C 3    ^C 5 ) ^T 20 )

Ф— C ⁰

4   3     22          2

z z a z a I a l a a 1

--------Y + z +--—— +---1-- k 12   3 8  2 82  k 8Jk82  8  3JJ

Здесь введены обозначения:

000  00   0  00

^C 1 = ^8T 11 , ^C 3 = ⁸ ( ^T 12 ^{+ T} 21)/ ² , ^C 5 = ⁸ ( ^т 21 ^T 12 )/ ² .

Система уравнений первого приближения

Система уравнений первого приближения строится на основе системы (15). После подстановки выражений сдвиговых слагаемых компонент скорости с учетом условия несжимаемости получим линейную неоднородную систему обыкновенных дифференциальных уравнений восьмого порядка с переменными коэффициентами. Здесь и далее будем явно указывать аргумент функций, известных к моменту решения очередной подсистемы уравнений. Уравнения системы записаны в порядке их решения. Уравнения градиентов давления:

Р о1 '= 0, <  = 0, Р о‘ '= 0, Р 2о' = 0, p j₂ '= 0, # = 0.                  (22)

Уравнения сдвиговых слагаемых компонент скорости разбиваются на две подсистемы:

Q1" = Re82 (2Q0? + Q0'W1), y1 = Re 82 (Р2о — Рок + 2/0? + у’" W1),                        (23)

у 2 " = 8 ² Re ( Р 11 +2 / 0? + у 2'W ¹ ) .

Механика

Уравнение скорости изменения площади элемента жидкости, вертикальной компоненты скорости жидкости и фонового давления на свободной поверхности:

1        2   1     1      01     01      0  1

^  — Re &  \ P 2° + Р )2 + 2 / 1 / 1 + 2 / 2 / 2   212 12 I,

W¹ —- 2 ^ 1 ,

W 1 " — Re P ° " .

Уравнения фоновых слагаемых компонент скорости

< — 5 ² Re ( _Z “ U + ( Y - 2 0 ) V 01 + P ) + U ( £ 1 + Y ) + V o0 ( Y -2 1 ) + U^W 1 ) ,

V)"— 52Re((Y0 + 2°)U -YV) + Pi + Vo°(^1 — Y1) + O/. +21)).(25)

Граничные условия для систем (22)-(25) на твердой границе:

5U1(°) — aU1 (°), Y'(°) — aY1 (°), 52"(°) — a^2 ( °), V( °) — aV°1 (°), 521" (°) — a21

5 ? " ( ° ) — a ? ( ° ) , W ¹ ( ° ) — °;

на свободной границе

U 1 " ( 1 ) — °, V ¹ " ( 1 ) — °,

^£ "  ( 1 )^— (^ 1 ^{+ t} 22 )/ ( ^{2 5} ) , ri "  ( 1 )^— ( ^т п ^{- т} 22 )/ ( ^{2 5} ) , y 2 ' ( 1 )^— ( ^т 12 ^{+ т} 21 )/ ( ^{2 5} ) ,

21" (1) — (т21 T)/(25), P^ (1) — °, P)2 (1) — °, P11 (1) — ° .(26)

С помощью простых преобразований задача интегрирования системы (22)–(25) сводится к последовательному взятию нескольких квадратур. Из первой подсистемы (22) следует, что градиенты давления постоянные. Общее решение системы первого приближения (23), (24) получено в виде суммы многочленов переменных z и а/ 5 :

£

Q ^f z + a 1 + Q ₂ Re 5³ 2 L 5 J

z a z

3 ⁺ 5 [ У

— z —

1 A 2 < 2

1 1 a z

3 ] ⁺ 5 2 [ T

—

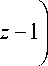
a

,

1 cnl a z 1  Q? Re5 ma          2э Л3а 3

W ¹ — — 5 zQ —+— + —----- z 6°— 7 — 1°—7 z ² — 3 z — 6 — 5— z ³ — 6 z — 4 — z z ³ — 1°

1L 5  2 J 3° I 5      52 V            ^5^                 \

Y 1 — ⁵ 1 ^ 11 — T 22 ) ^f z + a У Re C ° Q 1 5³

2 ^х         ' L о J

1 a 2   1 a 3 z

--V z +

^ 2 52     6 524

f     a 1a     1 a1 z ++1

L    5 JL 5 ²   2 5  6 JJ

+

+ Re ² C ₁ ° 2 ⁵

z ⁵ a ²   z ⁶ a z ⁷    f    a 1C a ⁴   8 a ³   5 a ²    8 a 4

--- +--+--+ z + - 2— +--- +--- +--+ — 15 5 ²   45 5  315   L    5 JL 5 4   3 5 3   3 5 ²   15 5  45

1    5 f a

Y —     +

²    2 L 5

+ Re ² C ° 5 <

z ⁴

+

3 ^a

L 5 3

—

a ²

—

a 1     ₂ f a z 1 a a 1 a

5 3 ^J~^z L 5⁺3 ^J L 5 3 ⁺3^ ⁺3 5 _J

z^ + T 21 ) + Re C ° Q 5 ³

5 2Л z a   f a

+ + z

15 5 ²   L 5

22 za

+1

2 5 ²    6 5  24

—

z ³ a z ⁴

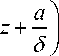
z ³

Q 2 ,

a     1 a    1 1

++

L 5 ²   2 5  6J J

+

, a ⁴    8 a ³    5 a ²    8 a   4 ¹

2 +7+7++

L 5 ⁴   3 5  3 5 ²   15 5  45 J

—

T^{+ z}

L

2 ^a

Л 3

a    a    1 a 1

++ г

L 5³  5 ²   3 5 J

z ⁶ a   z ⁷    z ^{4 f} a ³    a ²    a   1 ¹

+++ Q 2 ,

45 5  315  12 L 5 ³   5 ²   5  3 J

² 1 ( z ■^{) =} 32( -5 ⁺ z ) ( T 21 ^— t ) -3 0^R e ⁵ 3 1 ₅ — 2 ₅ ( - •² — ² z — 1 I — 6 5 ( -■ ³ — ³ z ^— 1 ) — 24 ( - •^{3 —} 4 ) 1 +

+

C 5⁰ 1260

Re ² 5 5

2520 a r - 420 a  3 z ² - 6 z - 8 + 105 a- (20 + 32 z - 12 z ² - 4 z ³ + z ⁴ +

5 5        5 4                       5 ^{3 v}                             ’

+ 21 a ^ ( 32 + 100 z - 20 z ² - 20 z ³ - 5 z ⁴ + 4 z ⁵ ) + 7 a ( 16 + 96 z - 20 z ³ - 15 z ⁴ + 4 z ⁶ ) +

+ z ( 112 - 35 z ³ + 4 z ⁶ ) ] Q ₂.

Решения системы первого приближения содержат два слагаемых: одно с множителем Q1 = T11 + 722, второе с множителем

01  01  01  01

Q 2 = ^T 11 ^T 11 ^{+ 7} 21 ^T 12 ^{+ T} 12 ⁷ 21   ^T 11 ⁷ 22 ^{.                           (27)}

Первое слагаемое описывает влияние на решение системы первого приближения отклонения от условия несжимаемости (12), а второе – влияние отклонения от условия совместности (13).

Если выполняются равенства Q ₁ = 0 и Q ₂ = 0, то решение системы первого приближения принимает вид:

1  5          ( a ^   1  5 ( a ^                 5 (a ^

/1 = 2(^11 - T22 'I z + ~5) , Y2 = 2^  z Д12 + T21) , Q =2^  z J(T21 - T12 ), S = 0 , W = 0 .

Вертикальная компонента скорости и скорость изменения площади элемента жидкости обращаются в нуль, течение при выполнении указанных условий остается слоистым.

Первые приближения фоновых слагаемых горизонтальных компонент скорости строятся по той же схеме, что и фоновые слагаемые нулевого приближения. В результате получаются полиномы высокого порядка, которые за громоздкостью не приводятся.

Граничные условия следующих приближений (m > 1) на свободной границе берутся однородными £т' (1) = 0, Ym' (1) = 0, Ym' (1) = 0, ^m' (1) = 0. Решения получаются в виде многочленов переменных z и а/5 .

Ниже приведены результаты вычислений решений системы первого приближения (23), (24) при некоторых вариантах значений параметров.

Вариант 1. Параметры системы и градиенты давления:

Re = 10, 5 = 0,1, а = 0, P 0 = 1, P ₀ ⁰1 = 0.

Невозмущенные касательные напряжения:

Т ⁰ = 10,0, т 0 = 0, т ^ = 1,0, т 1⁰₂ =- 1,0, т 21 = 1,0 .

Возмущения касательных напряжений: 7 11 = 0,01, 7 12 = 1,0, 7 22 = 0,1 .

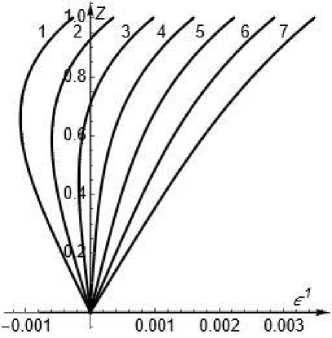
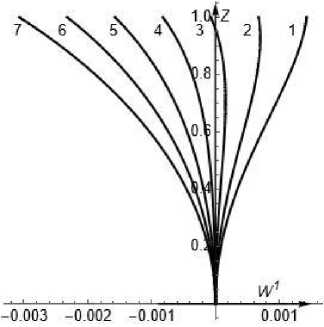
a                                                            b

Рис. 1. Профили скорости изменения площади элемента жидкости (a) и вертикальной компоненты скорости (b) в зависимости от возмущения касательных напряжений т^