Изучение качественных закономерностей процесса эвтрофирования мелководного водоема на основе математической модели биологической кинетики

Большое количество гидрофизических исследований водных экосистем и трофических цепей направлено на анализ трансформации вещества и энергии в них. Благодаря этим исследованиям в гидробиологии достигнуты большие успехи в понимании механизмов функционирования водных экосистем. В работах ученых Секерци Ю. и Петровского С. рассматривается процесс планктонно-кислородной динамики, учитывающий изменение физических характеристик океана, что, в свою очередь влияет на смертность не только планктона, но и других популяций [1]. Изучением воздействия человека на водную среду занимались Мюррей Дж.В. и Тайлефер М. В их работах исследуется регулирование, а также превышение стока рек и осадков над испарением; вынос загрязняющих веществ в водные объекты вследствие судоходства и стока речных вод; вертикальные плотностные градиенты и ослабление процесса перемешивания вод. Так, в работе [2] исследованы процессы межвидового взаимодействия, описаны потоки веществ, поступающие от одних элементов экосистемы к другим. Вопросами формирования структур в аэробных, субкислородных и анаэробных условиях занимался Еремеев А.П. Исследованием пространственного распределения профилей кислорода и сероводорода в поровых водах, а также расчeтом потоков этих компонентов занимались Орехова Н.А. и Коновалов С.К. Изучением процесса самоочищения загрязненного участка реки занимались Давыдов А.С. и Михайлов М.Д., Виноградов М.Е. Они разработали математические модели, учитывающие скорость поступления кислорода, потоков органических веществ, дефицит и скорость убыли кислорода за счет разложения придонных отложений и дыхания растений [3].

Под эвтрофированием зачастую понимается весь комплекс негативных явлений, приводящий к изменению трофического статуса водоема. При эвтрофировании обычно происходит накопление вещества, приводящее к нарушению функционирования лимнистических экосистем. В результате в водоеме возникает дефицит кислорода, резкие колебания биомассы водорослей, изменение таксономического состава сообществ гидробионтов.

Работа посвящена изучению процесса эвтрофирования мелководного водоeма с помощью методов и средств математического моделирования. Разработанная авторским коллективом пространственно-трeхмерная математическая модель биологической кинетики численно реализована в виде программно-исследовательского комплекса.

Применение равномерной прямоугольной сетки, которая является широко применяемой и многофункциональной, дает возможность дискретизировать поставленную гидробиологическую задачу [4]. Однако есть вероятность, что данный аспект приведет к образованию погрешности решения задачи на границе расчетной области. Такой недочет возможно значительно уменьшить с помощью применения метода частичной заполненности ячеек, который дает возможность увеличить точность построения задач биологической кинетики береговых систем [5]. Применение схем ≪ кабаре ≫ и ≪ крест ≫ , на основе линейной комбинации [6] дает возможность построить дискретную модель. Такой подход позволяет увеличить точность моделирования, если значения сеточного числа Пекле достаточно большие. На базе математического моделирования существует возможность формирования сценарного подхода для анализа критических явлений эвтрофикации и аноксии береговых систем мелководных водоeмов [7].

1.    Постановка задачи

Модель процесса эвтрофирования Азовского моря базируется на работах Ма-тишова Г.Г., Тютюнова Ю.В. [8], Ильичева В.Г., Сухинова А.И. [9], Четверушки-на Б.Н. [10], Якушева Е.В. [11], Вайнер Э.Р. [12], посвященных моделированию гидрохимических процессов. При разработке математической модели был сделан упор на то, что при разных сценариях ветрового волнения в прибрежных системах Юга России в придонных слоях увеличивается вероятность образования анаэробных условий. Исследования Трегер П., Ковет Г. показали, что восстановление поверхностного водонасыщенного ила сопровождается высвобождением ряда химических соединений, а именно: сульфатов, двухвалентного марганца и железа, органических соединений, аммония, силикатов и фосфатов [13, 14]. Модель представлена системой уравнений для каждого c _i – значения концентрации i-й субстанции следующего вида:

^dcr + u^ + ' + (w - W gi )= ^ - A c - + -^ (v - ^dc ⁱ ) + ^ - , ∂t ∂x ∂y           ∂z           ∂z ∂z

^ 1 = g i ^(c i , ^c 3 , ^c 8 , ^c 9 ) ^{— A} i ^c i , ^ 2 = ^g 2 ^(c 2 , ^c 4 , ^c I0 ) ^{— A} 2 ^c 2 ,

^ 3 = Y 3 a 2 (c 4 )c 2 c 3 — g 3 (c i , c 3 ) — A 3 c 3 + В(с з — c 3 ) + f,

^ 4 = ^A i ^c i + ^A 2 ^c 2 + A 5 ^c 5 ^{— g} 4 ^(c 2 , ^c 4 , ^c 5 ),                           ⁽¹⁾

^ 5 = ^g 5 ^(c 4 , ^c 5 , ^c 8 ) ^— A 5 c 5 , ^ 6 = ^(g 6 ^(c 4 , ^c 8 ) ^— А б ^)c 6 , ^ 7 = ^g 7 ^(c 6 ) ^— A 7 c 7 ,

^ 8 = (g 8 (c 2 ,c 7 ) — A 8 )c 8 — Y 8 a i^ )c i ,^ 9 = g 9 (c i ) — A 9 c 9 ,

^10 = gi0(ci, cio) + Y2a2(ci0)c2 — (aici + Y7c7)cw, где U = (u, v, w) - вектор скорости водного потока; wg. - скорость гравитационного осаждения i-й компоненты; △ - двумерный оператор Лапласа; ^vi - горизонтальный и вертикальный коэффициенты турбулентного обмена соответственно; ψi – химико-биологический источник (сток) или член, описывающий агрегирование (слипание-разлипание), если соответствующая компонента является взвесью, индекс i указывает на вид субстанции, i = 1,10. При построении модели параметризованы процессы биогеохимических циклов химических элементов, ответственных за трансформацию аэробных условий в анаэробные.

Функции зависимости скорости роста фитопланктона и бактерий от температуры (T), солености (S) (по Леману) и освещенности (I) (по Стилу) имеют вид:

ф т (Т, S,I ) = II- exp

{ 1 - am      1 ² - вт [^ 1 ² - Л

,m = { 1, 2, 5 } ,

Topt                   Sopt          Iopt где I(h) = Ioexp(-6h); h - глубина водоема; Iq - суммарная солнечная радиация на поверхности водоема; θ – коэффициент затухания, пропорциональный концентрации взвешенных в воде веществ (фитопланктона и детрита); Topt, Sopt – температура и соленость, оптимальные для данного вида гидробионтов; αm , βm – коэффициенты ширины интервала толерантности фитопланктона и бактерий к температуре и солености соответственно.

Расчетная область G представляет собой замкнутый бассейн, ограниченный цилиндрической боковой поверхностью а, невозмущенной поверхностью водоема X _o , дном X H = X H (x,y ). X - кусочно-гладкая граница области G, X = X _o U X H U а, 0 <  t <  T o . Пусть U n - нормальная составляющая поля скорости водного потока, и -вектор внешней нормали к X.

Добавим граничные условия:

∂ci ci = 0 на а, если Un < 0; —— = 0 на а, если Un > 0;

∂n

∂c i ∂z

∂c i

-€ i c i на X h , — = ^(c i ) на X o , ^(c) =

YA, i G { 3,4, 6, 7 } ;

(K i - C i ), i = 10;

0, i G { 1,2, 5, 8, 9 } ,

где a 0 – коэффициент аэрации; K 10 – концентрация растворенного в воде кислорода при насыщении; ǫ i – коэффициент поглощения i-й субстанции донными отложениями, i = 1,10. К модели добавляются начальные условия вида:

C i | t=o = C io (x,y,z), i = 1,10.

Для определения условий существования и единственности решения задачи (1)– (3) непрерывная модель линеаризована и аналитически исследована методом построения аналога функционала энергии. Результаты сформулированы в виде теорем.

Теорема 1. Пусть c i (x,y,z,t), ^ i G С^Ц ) П C(Ц ) , где Ц = G x (t o ,T q ); ^ i = const > 0 ; U = (u,v,w - w gi ),v i (z) G C 1 (G) ; c _{i 0} G C (G), i = 1,10 . Тогда при выполнении неравенств: max { ^ i , v i } - ^^ max {| p i |} > 0 для всех i = 1,10 , где ^ i = p i (c j )c i + ^ i , i = j; ^ i = Lc i - Dc i - p i c i , Lc i = ^ + div(c i U i ) , Dc i = ^ i A c i + d^dZ (vi^ ) , A q = n ² (1/l X + 1/1 У + 1/1 2 ) ; l x , l _y , l z — пространственные максимальные размеры расчетной области; задача вида (1) – (3) имеет решение.

Теорема 2. Пусть c i (x, y, z, t), ^ i E C ² ( Ц _t ) П C(Ц _t ) , ^ i = const > 0 ; U , v i (z) G C ¹ (G) , i = 1,10 . Тогда при выполнении неравенств: 2^ i (1/l 2 + 1/i y ) + 2v i /l 2 >  ^ i для всех i = 1,10 (функции ^ i определяются источниками загрязняющего вещества (ЗВ)) задача биологической кинетики вида (1) – (3) имеет единственное решение.

2.    Метод решения задачи

В работе [15] было проведено исследование алгоритма для решения многомерных задач диффузии-конвекции на основе схемы расщепления на явно-неявную задачи. Также была описана примененимость данного алгоритма для решения трехмерной задачи транспорта взвесей в прибрежных системах. Схема расщепления по пространственным координатам позволяет сократить обмены информацией, которые реализуются между соседними потоками при переходе с одного временного слоя на другой параллельным способом в приграничных узлах подобластей при геометрической декомпозиции трехмерной сеточной области.

Рассмотрим аппроксимацию трехмерной задачи биологической кинетики на примере уравнения диффузии-конвекции-реакции:

c t + ^(uc) X + ^(vc) y + ^(wc) Z = (ИХ + ++ ) y ^{+ (vc} Z ) Z ⁺ f             ⁽⁴⁾

с граничными условиями:

сП (x,y,z,t) = anc + вп, где u, v, w – компоненты вектора скорости водной среды, µ, ν – коэффициенты турбулентного обмена в горизонтальных и вертикальном направлениях, f – нелинейная функция правой части.

Введем равномерную расчетную сетку по времени:

ш T = { t n = пт, n = 0, N t , N t T = T } .

Проведем дискретизацию трехмерной задачи вида (4) на основе схем расщепления по физическим процессам (перенос веществ по каждому из пространственных направ-

лений): „n+1/3   п —т— + u(c“)X = G(c“)X)X,                   (5) n+2/3 _ n+1/3                                 . ‘ c T        + v(c"+1/3)y = ^(cn+1/3)y)y,                     (6) n+1    n+2/3 -------------+ wc{ = (vc{ )Z + f,                          (7) τz где cn – концентрация химико-биологической субстанции на текущем n-м временном слое tn , cn+'2/3 - на промежуточном (n + 2/3) временном слое, cn+1 - на последующем (n + 1)-м временном слое, с = (cn+1 — сп+2/3) /2.

• 2.1.    Линейная комбинация разностных схем ≪ кабаре ≫ и ≪ крест ≫

Рассмотрим задачу биологической кинетики на примере задачи транспорта веществ, выраженную нестационарным уравнением конвекции:

c t + uc X = 0,

где t Е [0, T], x Е [0, L]; c (x, 0) = c ⁰ (x); c (0,t) = 0, если u >  0 и c (L,t) = 0, если u <  0, u = const.

Введем равномер ную по времени и пространству сетку CD = Go h * ш _т , где ш h = {x i | x i = ih, i = 0, N x , N x h = L} , N x - количество шагов по пространству, L -максимальный размер области вычислений; ш _т = {t ⁿ | t n = пт, п = 0,N _t , N t т = T }, N t – количество временных слоев, T – верхняя граница по времени.

Запишем классические схемы, используемые для численного решения задачи (8):

• - схема « кабаре » для случая и ^ 0 :

  – схема ≪ крест ≫ :

  
  

  n+1    n

  c i    ^— c i

  
  

  2т

  
  

  +

  
  

  c

  
  

  n

  i -1

  
  

  n -1

  ^c i -1

  
  

  2 т

  
  

  ⁿ c _i + и—

  
  

  _-

  
  

  c

  
  

  h

  
  

  n

  i -1

  
  

  = 0;

  
  

  n +1     n -1

  c _i    - c _i

  
  

  2 т

  
  

  + и

  
  

  n ^c i +1

  
  

  _-

  
  

  n

  i -1

  
  

  2 h

  
  

  = 0.

  
  
  
  

В результате разложения членов разностных уравнений (9), (10) в ряд Тейлора [16]

получим соответственно:

n +1     n -1

c _i    — c _i

2 т

n +1     n

-i    ^— c i +

2т   +

+ и

n ci+1

(г —

—

2 h

n i-1

n -1 ^c i -1

2 т

n

ci

+ и-

1>^ЗГ — 1 uh

n i-1

—

h

n i-1

()

n i-1/2

∂c ∂t

∂c

⁺ "т^ )

∂x

n i-1/2

+ O (т ⁴ + h⁴)

—

= fdc dc^ ⁿ

∂t   ^u∂x _i

—

r ²

uh ²

(1x3) “ + O ( т ⁴ + ^h 4 ) , (12)

где r = ит/h - число Куранта.

Линейная комбинация разностных схем ≪ кабаре ≫ и ≪ крест ≫ , взятых с весами 2/3 и 1/3 соответственно, с учетом (11), (12) запишется в виде:

n +1 n c _i    — c _i

τ n+1    n i — ci

τ

+ 2

+ 2

n ^c i -1

n ^c i +1

n -1

^c i -1

3т

n -1

^c i +1

3 т

+

+

n    n -1

_i — c _i

n

ci

3 т

—

n -1

ci

3 т

n ci+1 i+1

n ci+1

+ и -+-

+ 4c ⁿ — Sc n-!

3h

— 4c n — bcn_ -

3h

= 0, если и >  0;

= 0 , если u <  0 .

Данная разностная схема имеет локальную погрешность аппроксимации

r (1

— r ) uh ²

^{(d 3 c/d}x ^{3 ) n}--/3 J

6 + O (т ² + h ³ ) относительно фиктивного узла (i — 1/3, n).

Получили, что порядок погрешности аппроксимации линейной комбинации раз-

ностных схем ≪ кабаре ≫ и ≪ крест ≫ с весами 2/3 и 1/3 соответственно выше, чем у

исходных схем.

Найдем аналитическое решение уравнения (8), для чего представим его в виде конечной суммы ряда Фурье в комплексной форме:

N c (x,t)= ^2 Cm (t) exp (j^mx),                       (14)

m =- N

L где ш = п/L,m - номер моды, Cm (t) = -2 J c (x, t) exp (j^mx) dx, Cm - комплексная 0

амплитуда m-й моды, j ² = — 1.

Подставляя (14) в (8), получим:

N                            ^′ N                            ^′

I ^2 C m (t) exp (jumx) I + u I      C m (t) exp (jumx) I = 0.

\m=-N                  )t     \m=-N                  /x

Изменяя порядок операций дифференцирования и суммирования ряда, полагая функцию exp (jumx) линейно независимой, получим:

(C m (t)) t‘ = - (juum) C m (t) .

Из (15) получим выражение для C m (t) и подставим его в (9). Таким образом, аналитическое решение уравнения (8) примет вид:

N c (x,t)= ^2 Cm (0) exp (—juum t) exp (jumx).               (16)

m=-N

Исследуем точность разностной схемы вида (13). Для этого подставим выражение (13) для (x i , t) в узле x i = ih в (14) (рассмотрим случай u ^ 0). Проведем несколько элементарных алгебраических преобразований, учтем, что функции exp (jumx) линейно независимы, получим:

p n+1 m

-

n

m

τ

+ 2

n

m

-

p n—1 m

3т

exp ( — jumh) +

n

m

-

n—1

m

+uC mⁿ

exp (jumh) + 4

-

5 exp ( — jumh)

3т

+

3h

= 0.

Выражение (13) при т ^ 0 примет вид:

‘  ( ^exp⁽j^{umh)+4 —}       jCmhA

(C m (t)) _t = u----- 2h (2 +exp ( — jumh))----- ) C m '            ⁽¹⁸⁾

С учетом (15) решение, полученное с использованием схемы (13), соответствует решению уравнения c t = — u * c X , где u * = u (1 — a 1 ), a 1 = 1 — exp^mhH ^{4 — 5ex} p ^{( —} j^um^{h )}                                         _

. Произведя несложные алгебраические преобразова- 2jumh (2 + exp ( — jumh))

ния, получим а 1 = j hmmh ) + O ( (umh) ⁴ ) . Из полученного выражения видно, что схема (5) аппроксимирует конвективный член с третьим порядком точности по пространству.

Легко показать, что при h ^ 0 из выражения (17) следует, что разностная схема (13) имеет погрешность аппроксимации по времени O (т ² ). Таким образом, разностная схема (13) для задачи (8) имеет погрешность аппроксимации, равную O (т ² + h ³ ).

• 2.2.    Разностные схемы для решения уравнений конвекции-диффузии-реакции

Расчетную область впишем в прямоугольник. Построим равномерную по пространству сетку:

u h = {x i = ih x , y j = jh y , Z k = kh z ; i = 0,N x , j = 0,N y , k = 0,N z ;

N x ^h x    l x , ^N y h y    l y ,

^N z ^h z    l z } ,

где h _x , h _y , h _z – шаги в направлениях пространственных координат, l _x , l _y , l _z – максимальные размеры расчетной области.

Для аппроксимации двумерного уравнения (5) в направлении горизонтальной плоскости xOy на основе линейной комбинации разностных схем ≪ кабаре ≫ и ≪ крест ≫ с учетом заполненности расчетных ячеек будем использовать схему расщепления по пространственным направлениям. Разностная схема для уравнения (5), описывающего перенос в направлении Ox, записывается в виде:

n +1 / 3

29 2 + 9 0 c i j ,k

-

n ci j k

-

nn ci,j,k    ci-1,j,k

+ 5ui-i/2,j,k q2

-cn      2∆ cn    q +x∆ cn q i,j,k          x i-1,j,k q2     x i,j,k q0

3hx     + n         nx                 nn ci+1,j,k - ci,j,k                     ci,j,k - ci-1,j,k

= 2+i+i/2,j,k qi-------h22+i-i/2,j,k q2h

| q 1 - q 2 | µ i,j,k

τ

c

+u i+i/2,j,k min (9 1 ,9 2 ) -

n i+1,j,k

-

-

-

-

-

^a x c i,j,k ⁺ Д

h x

-,U i,j,k >  0;

n +1/3

2q i + q o c i j ,k

-

τ

c n                  c

——--+ 5u i+i/2,j,k 9i —

n i+1 j k

-

3h x

n ci j k

+ U i-i/2,j,k min (q i ,9 2 )

n ci j k

-

n ci-1,j,k

+

^2A x c n+ijk q i + A x c njk q o

= 2^ i+1/2,j,k q 1

n ci+1,j,k

-

n ci j k

-

| q 1

-

_h 2 _x

-

n ci,j,k

² ^ i-i/2,j,k 9 2------

-

3h x

n ci-1,j,k

_h 2 _x

+

I      ^a x c njk ^{+ e}x        _n An _ c+jV

+ 1 ^ц i,j,k      7        ,^u i,j,k < ⁰, где ^A x c i,j,k =        '

h _x

-

n -1 ^c i,j,k

.

τ

Разностная схема для уравнения (5), описывающего перенос в направлении Oy, записывается аналогично. Здесь и далее коэффициент заполненности расчетной ячейки зависит от номера ячейки, то есть q o = q o,i,j,k , q i = 9 i,i,j,k , ..., 9 б = 9 6,i,j,k • Для аппроксимации уравнения (6) в вертикальном направлении используется явная схема:

n +1

^c i,j,k q 0

-

τ

c n +2 / 3                 c

-^j,--+ ^q 5 ^w i,j,k+1/2 —

n +5 / 6 i,j,k +1

-

n +5 / 6 ^c i,j,k

n +5 / 6 ^c i,j,k +1 = 9 5 V i,j,k+i/2--------

-

n +5 / 6 ^c i,j,k

2h z

n +5 / 6 ^c i,j,k

^{+ 9} 6 w i,j,k- i/2-------:

-

n +5 / 6

c i,j,k-i =

^h z ²

n +5 / 6 ^c i,j,k ^{+ 9} 6 ^v i,j,k- i/2--------

2h z

-

^h z ²

n +5 / 6

i,j,k -1 n

⁺ f i,j

Уравнение (20) решается методом прогонки, что значительно сокращает время расчетов.

• 2.3.    Тестирование разработанной разностной схемы

Рассмотрим начально-краевую задачу для нестационарного уравнения теплопроводности:

c t = цс' Хх + f i ,                                     (21)

где t E [0, T] , x G [0, L]; c (0, t) = 0, c (L, t) = 0, c ₀ (x) = 0(20 — x) — 0(10 — x) , где 0(x) - функция Хэвисайда; ц = 1 м ² /с.

Для численного решения задачи (21) будем использовать схему с весами:

n+1 n i - ci

τ

= ц

n + σ ^c i +1

-

2c ^{n + CT}

+c

n + σ i -1

h ²

+ f _i ,

где с П ^{+ ст} = ac n ⁺ⁱ + (1 — а) с П , а E [0,1] - вес схемы.

Необходимое условие устойчивости для явной схемы, полученное на основе метода гармоник, имеет вид неравенства [17]: y = T^/h 2 > 0, тогда 4y sin ² (ha/2) <  4y ^ 2 ^ Y ^ 1/2. Таким образом, получили т ^ т _тах = h ² /(2д). Несмотря на то, что данная оценка является жестким ограничением для явных разностных схем, на практике шаг по времени необходимо брать ещe меньше.

Параметры расчетной сетки задавались следующим образом: шаг по времени находится в диапазоне от 0,001 до 10 c, шаг по пространству h =1 м, длина интервала по времени T составила 60 с. На рис. 1 представлен график погрешности решения модельной задачи (21) на основе схемы (22): кривая 1 – явной схемы, 2 – явной схемы с весами (а = 0, 5).

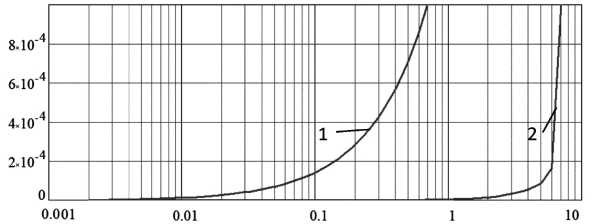
Рис. 1 . График зависимости погрешности аппроксимации от шага по времени τ 0 : 1 – для явной схемы, 2 – для схемы с весами

Запиш ем выражение для расчета погрешности вычислений в норме пространства

L2: Ф = /^ (ci — ci)2/ ^ с2 , где ci - точное значение решения задачи (21) в узле i, ci -ii численное решение, зависящее от величины шага по времени. По горизонтальной оси отложена величина шага по времени т0 , отнесенного к величине ттах (т0 = т/ттах) .

Для того чтобы относительная погрешность явной схемы была равна 0, 01%, необходимо величину τ 0 брать равной 0,0717, в случае использования предложенной схемы с весами параметр τ 0 равен 5,1858.

Рассмотрим решение начально-краевой задачи (8) при и = 0, 5 м/с и начальном значении с ⁰ (x) = 9 (70 — x) — 9 (60 — x) с ₀ (x) = 9 (20 — x) — 9 (10 — x), где 9 (x) - функция Хэвисайда. Введем выражение для погрешности решения в норме пространства L ₁ : Ф ^п = 13 Ф П h, Ф п = | с П — c (x i , t n ) l , где с (x i , t n ) — точное решение задачи (8) в узле i

• i,    c_iⁿ– численное решение. На рис. 2 представлены графики значений погрешности аппроксимации численного решения задачи (8) с использованием схем ≪крест≫, ≪ка-баре≫, а также их линейной комбинации при различных значениях чисел Куранта (r = |u| т/h, 0, 01 ^ r ^ 1). Шаг по временной сетке т менялся от 0,02 с до 2 с при

3.    Результаты численных экспериментов

величине временного интервала 100 с.

Из рис. 2 видно, что предложенная разностная схема (20) точнее описывает решение нестационарного уравнения конвекции при малых значениях чисел Куранта r ^ 0,1. Из расчетов для уравнения теплопроводности известно, что т ^ А • ттах, ттах = h2/2д, А = 0, 01 - отношение шага, при котором достигается необходимая точность расчетов и τ остается в приемлемом диапазоне, к шагу, полученному из ограничения на устойчивость явной схемы ттах. Тогда А |u| т/h ^ 0,1, где сеточное число Пекле Pe = |u| h/д ^ 0, 2/А = 20. Отсюда получаем диапазон сеточных чисел Пекле, при которых предложенная разностная схема (20) будет аппроксимировать конвективный член с лучшей точностью, чем классические схемы: 2 < Pe ^ 20, в работе [16] показано, что при Pe ^ 2 более высокую точность дает центральноразностная схема.

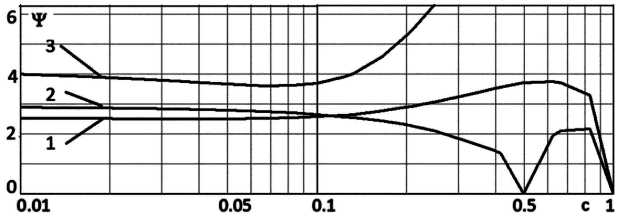
Рис. 2 . График зависимости погрешности численного решения задачи (8) от значений чисел Куранта с использованием разностных схем: 1 – (20); 2 – ≪ кабаре ≫ ; 3 – ≪ крест ≫

На базе разработанного программного комплекса, ориентированного на вычислительную систему с распределенной памятью, был проведен численный эксперимент для задачи биологической кинетики (1) – (3). Также был изучен процесс эвтрофикации мелководного водоема в летний период, механизм самоочищения мелководного водоема с учетом влияния жизнедеятельности аэробных и анаэробных бактерий. Проведен анализ влияния поступающих в водоем биогенных веществ, пространственного распределения солености, температуры и освещенности на рост и смертность клеток фитопланктона в реальной области сложной формы (прибрежная система – Азовское море). При моделировании учитывалось влияние как абиотических, так и биотических факторов на развитие основных гидробионтов. При создании массивов входных данных использовались экспедиционные данные, электронный атлас Азовского моря [18].

Выполнен вычислительный эксперимент для моделирования превращений соединений серы (сероводорода H ₂ S, элементарной серы S, тиосульфатов S ₂ O 3 , сульфатов SO ₄ ) в присутствии растворенного кислорода и при его недостатке в фиксированной точке придонной области центрально-восточной части Азовского моря. На рис. 3 представлены различные сценарии превращений веществ (растворенного кислорода O ₂ и сероводорода H ₂ S), временной период моделирования – 23 дня, шаг по времени – 100 с. Численный эксперимент показывает, что при концентрации растворенного кислорода ниже 1,1 мг/л он полностью расходуется на окислительные процессы, при этом растет концентрация сероводорода. При увеличении количества гидратированных молекул кислорода в воде концентрация ядовитого сероводорода снижается и постепенно достигает нулевого значения. Чем выше в воде концентрация растворенного кислорода, например, вследствие активного перемешивания вод из-за ветрового воздействия, тем быстрее запускается процесс самоочищения водоема. Результаты эксперимента согласуются с данными, полученными в ходе экспедиций, и литературными источниками.

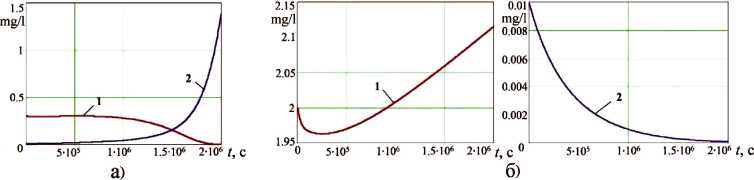
Рис. 3 . Изменение концентраций: 1 – растворенного кислорода c ₁0 , 2 – сероводорода c ₆ при а) недостатке кислорода (начальное значение сю = 0, 3 мг/л); б) достаточном количестве кислорода (начальное значение с ₁₀ = 2 мг/л)

Рис. 4 . Результаты численного эксперимента: концентрации а) фитопланктона c ₁ ; б) детрита c ₄ ; в) биогенного вещества c 3 (нитратов)

На рис. 4a представлено трехмерное распределение концентрации синезеленых водорослей, преобладающих в Таганрогском заливе, и диатомовых водорослей, распространенных в основной акватории, которые вносят основной вклад в образование детрита (рис. 4б) вследствие экскреции и отмирания, а также минерального питания (нитратов, рис. 4в). Временной интервал моделирования – 50 дней, что соответствует временному периоду от начала вегетации до бурного цветения водорослей в летнее время. Численный эксперимент показал, что наибольшая концентрация детрита наблюдается в Таганрогском заливе, так как в нем продуцируется основная часть биомассы фитопланктона. Взвешенные частицы детрита выносятся течением в основную часть моря, где, оседая на дно, могут вызывать явление аноксии при определенных ветровых и температурных режимах. Считается, что фотосинтез пропорционален скорости роста первичных продуцентов с постоянным для каждой группы коэффициентом ассимиляции. Процесс реаэрации дает возможность учитывать концентрацию насыщения растворенным кислородом, а коэффициент реаэрации есть функция скорости ветра. Основные процессы, расходующие растворенный в воде кислород, – это окисление детрита в толще воды и придонном слое и дыхание живых существ, в том числе фитопланктонных популяций. При моделировании трансформации кислорода учитывалась его изменчивость в соответствии со стехиометрическими соотношениями. В описании химико-биологического источника кислорода учтены другие процессы, приводящие к потере кислорода при окислении биогенных веществ. В балансовом соотношении для кислорода учитывался его поток через границу с атмосферой. В свою очередь, этот поток сильно зависит от температуры воды. Эксперименты показали, что рассматриваемый метод является достоверным для классического формирования фитопланктонных популяций в теплый период времени в Азовском море. Также существует возможность исследовать процесс эвтрификации и метод самоочищения вследствие развития бактерий, которые задействованы в процессе разложения детрита и возобновлении сульфата до сероводорода при анаэробном дыхании микроорганизмов, которые содержат соленость, температуру и освещенность, на продукционно-деструкционные процессы и явления фитопланктона.

Заключение

В результате проведенных исследований разработана модификация пространственно-временной гидрофизической модели динамики планктона, которая содержит в себе изменение концентрации фитопланктона, аэробных и анаэробных бактерий, биогенных веществ, с целью изучения гидробиологических процессов мелководного водоема. Применение сценарного подхода в разработанном программном комплексе позволило изучить влияние отсутствия аэрации водной среды и постоянного притока кислорода на процессы эвтрофикации водоема. Представлены и изучены условия, при которых не учитывается устойчивость круговорота веществ в экосистеме, изучен сценарий структуры водоема при неблагоприятном действии природных и техногенных факторов на жизненный цикл аэробных и анаэробных бактерий, принимающих участие в процессе аммонификации детрита.

Схема расщепления исходной трехмерной задачи вида (1) – (3) по геометрическим направлениям на двумерную и одномерную по горизонтальному и вертикальному направлениям соответственно позволяет ученьшить количество обменов пакетами данных между соседними потоками при переходе от одного временного слоя к другому параллельным способом в приграничных узлах подобластей на основе геометрической декомпозиции трехмерной сеточной области по вертикальным плоскостям. Дискретизация разработанной модельной задачи водной экологии была произведена на базе линейной комбинации схем ≪ кабаре ≫ и ≪ крест ≫ с учетом частичной заполненности расчетных ячеек.

Численная реализация поставленной задачи биологической кинетики дает возможность изучить как внутри-, так и межвидовые химические связи между планктонными популяциями прибрежной системы – Азовское море в режиме ограниченного времени, что является актуальным при возникновении экологических ситуаций катастрофического характера, к которым можно отнести эвтрофикацию и процессы экзогенной гипоксии. Установлено, что существенная неоднородность структуры детрита, вызванная различными фракциями природных органических веществ, играет важную роль в регулировании глобальных процессов водной экологии.

Исследование выполнено за счет гранта Российского научного фонда № 22-71-10102,