Изучение напряженно-деформированного состояния диафиза лучевой кости с краевым вырезом и компенсирующими элементами методом компьютерного моделирования

В различных областях реконструктивной хирургии для замещения дефектов тканей применяют пластику кожно-костным лучевым лоскутом [1, 2]. При всех своих очевидных преимуществах метод имеет существенный недостаток, обусловленный морбидностью донорской области, что препятствует его широкому применению. Забор кожно-костного трансплантата для последующего его переноса или перемещения в реципиентную область неизбежно вызывает образование краевого дефекта диафиза лучевой кости. Частота развития патологического перелома лучевой кости в области краевого дефекта достигает 31 % [3, 4]. Лечение пациентов с данным осложнением, вызывающим значительные функциональные и косметические нарушения кисти и предплечья, представляет значительную хирургическую проблему, сопровождается длительными сроками и существенными материальными затратами. Отношение специалистов к способам профилактики подобных осложнений остается неоднозначным. В литературе имеются противоречивые мнения о влиянии формы краевого выреза на прочность лучевой кости: от полного отрицания до значительного ослабляющего влияния [5, 6]. Большинство авторов в настоящее время признают целесообразность профилактической фиксации донорской лучевой кости [7, 8, 9]. Однако анализ работ по данной тематике показывает, что многие вопросы остаются дискутабельными, а мнения специалистов — противоречивыми [10]. В частности, не проведен сравнительный анализ влияния различных вариантов остеотомии на прочность кости, не обоснованы методы остеосинтеза, виды металлических пластин, количество, диаметр винтов, характер их проведения для фиксации пластины к кости, не изучены механизмы ослабления винтов. Оценку остаточной прочности кости и выбор способа профилактики перелома большинство авторов осуществляет на основании только клинико-рентгенологических данных [11, 12]. В связи с этим возникает необходимость изучения степени влияния указанных факторов на прочность кости для разработки и обоснования способов ее укрепления и профилактики патологических переломов. Эволюция программного обеспечения и компьютерной техники в последние годы позволила достичь крайне высокой достоверности (95–99 %) и наглядности имитации поведения изделия под воздействием различных, в том числе и механических нагрузок, вероятностную оценку надежности конструкций [13, 14]. В настоящее время одним из наиболее распространенных способов решения задач механики (в том числе биомеханики) является метод конечных элементов (МКЭ) [15]. Соответственно, моделью кости для численного решения задач прочности в биомеханике является конечно-элементная модель (КЭМ) [15]. Одним из основных параметров, который необходимо определить для оценки прочности материала, является уровень его внутреннего механического напряжения. Конечно-элементная имитационная компьютерная модель позволяет неинвазивно определять и прогнозировать механическую реакцию кости на различные нагрузки и предрасположенность (подверженность) к разрушению в области максимальных механических напряжений при нагрузках, обеспечивает наглядность, визуализацию, доступность анализа параметров всего объекта [16, 17]. Преимуществами МКЭ являются возможность исследовать конструкции, составленные из нескольких материалов любой формы, и осуществимость учета различных граничных условий [18, 19]. По данным литературы, МКЭ позволяет определить прочность лучевой кости, изучить стабильность ортопедических имплантатов, что способствует проведению мероприятий по профилактике переломов [20]. Вместе с тем, в доступной литературе имеются довольно противоречивые данные, полученные методами компьютерного моделирования, касающиеся механических свойств лучевых костей с различными формами краевой остеотомии, способов компенсации образовавшихся дефектов, фиксации пластины и укрепления кости при растяжении, сжатии, изгибе и кручении [21, 22]. Нет публикаций о влиянии кривизны кости на ее прочность. Кроме того, недостаточно обоснованы выбор вида пластины, количества и размеров винтов, а также характер их проведения с позиции напряженно-деформированного состояния (НДС) кости, не изучена продольная устойчивость модели с вырезом и пластиной [23, 24], что является сдерживающим фактором в разработке способов профилактики патологических переломов. В связи этим необходимы знания о характере распределения напряжений в неповрежденной кости и после формирования краевого выреза, а также в системе кость – фиксатор для адекватного определения метода профилактического укрепления кости.

Цель работы — представить результаты конечно-элементного анализа влияния краевого выреза различной формы, кривизны кости и способов увеличения ее прочности на НДС диафиза лучевой кости.

МАТЕРИАЛЫ И МЕТОДЫ

С помощью системы автоматизированного проектирования CAD создавали 3D–модели диафизарной части лучевой кости:

• —    без выреза и начальной погиби;

• —    без выреза с начальной погибью в одной (горизонтальной или вертикальной) или двух плоскостях;

• —    с треугольным вырезом и начальной погибью в одной или двух плоскостях;

• —    с прямоугольным вырезом и начальной погибью в одной или двух плоскостях,

• —    с подобными вырезами и погибью с накостными плоскими и полутрубчатыми пластинами, фиксированными двумя, четырьмя и шестью винтами различной длины и диаметра;

• —    с прямоугольным вырезом и компенсирующей вставкой, фиксированной двумя винтами.

Аналогичным образом создавали модели пары винт – кость с прямоугольным вырезом, замещенным идентичной по форме и размерам кортикальной вставкой, фиксированной винтами с укреплением кости пластиной.

Для определения напряжений выполняли расчеты МКЭ в программных комплексах ANSYS, Siemens NX. Для упрощения расчетов костную ткань диафиза лучевой кости считали сплошной, гомогенной, линейной, упругой (линейно-эластичной), непрерывной и изотропной. Принято, что компактная кость изотропна, так как она имеет общую пластинчатую и относительно однородную структуру, а характеристики прочности и упругости не меняются в пределах исследуемой диафизарной части кости.

Изучали объемное динамическое неразрушающее нагрузочное напряженно-деформированное состояние на линейно-упругой изотропной гибридной модели диафиза лучевой кости, подчиняющейся обобщенному закону Гука, с соблюдением гипотез технической теории изгиба балок, так как забор трансплантата в клинике в большинстве случаев осуществляют из этой части кости.

Оценку НДС проводили на основании третьей и четвертой теории прочности с использованием критерия Мизеса, дающего представление об общей интенсивности напряжения, а также объединяющего нормальные и сдвиговые напряжения, действующие на объект. Выбор данного критерия, обычно применяемого для характеристики свойств вязкого материала, обусловлен использованием в модели металлических компенсирующих элементов (пластина, винты).

Изучали влияние на максимальное напряжение кости следующих параметров: форма и глубина выреза, кривизна кости в одной или двух различных плоскостях, характер компенсации дефекта, а также вид пластины, ее размеры (ширины, длины, толщины), количествл пластин, способы проведения и размеры винтов, фиксирующих пластину к кости с прямоугольным и треугольным вырезом.

Кроме того, оценивали критические напряжения при исследовании кости на продольную устойчивость. На первом этапе исследования проводили построение пространственной геометрической модели кости, далее с помощью программы генерации конечно-элементной сетки модель разбивали на конечные элементы (КЭ). Сложная трехмерная геометрия диафиза лучевой кости, проведенный анализ построения и поведения различных КЭМ определили выбор трехмерной КЭМ кости.

Для формирования объемной твердотельной сетки в качестве типа КЭ использовали 10-узловой изо-параметрический тетраэдрический элемент второго порядка (СTetra 10). Элементы имели три степени свободы в каждом узле. Перемещение вдоль координатных осей является оптимальным для отображения объектов неправильной формы со сложной геометрией в используемых программных комплексах.

Для построения трехмерной линейной КЭМ модели использовали срезы анатомических препаратов лучевой кости. Геометрическая расчетная модель представляла собой цилиндрическую конструкцию с поперечным сечением, составленным из полукольца и двух боковых симметричных относительно общей оси трапеций. Геометрия сечения кости, первоначальная кривизна кости в двух плоскостях соответствовали реальным средним размерам, полученным экспериментально на кадаверном (анатомическом) материале. На втором этапе задавали физические характеристики материалов модели. Модули упругости и коэффициент Пуассона различных материалов, используемые при расчетах, взяты из литературных первоисточников или получены в эксперименте. Для костного материала приняты следующие механические характеристики: модуль Юнга принят равным 0,2×10⁵ МПа, коэффициент Пуассона (коэффициент поперечных деформаций) — 0,3, предел прочности — 120 МПа, плотность ρ = 2400 кг/м³. Для пластин и винтов, состоящих из титана ВТ6, модуль Юнга равен 1,15×10⁵ МПа, коэффициент Пуассона — 0,32. Коэффициент трения μ для контактной пары металл – металл принят равным 0,15, а для пары кость – металл — 0,3. Приняты допускаемые нормальные напряжения при растяжении 60 МПа из условия 0,5 от предела прочности (двукратный запас прочности). При кручении допускаемые касательные напряжения, как правило, принимают равными 0,5 от нормальных (в соответствии с третьей гипотезой прочности, то есть 0,25 от предела прочности). В наших случаях принято приблизительно 0,2 от предела прочности. Относительная глубина треугольного и прямоугольного вырезов h 0 /H составила 0,16 и 0, 33 (H — высота сечения неповрежденной кости, h 0 — глубина выреза).

Смоделирована погибь кости в двух направлениях: x = 3,73 мм; y = 6,38 мм. Кроме того, построена модель пары винт – кость. Созданы упрощенные модели фиксаторов различной толщины (1 мм, 2 мм, 2,5 мм, 3 мм) для плоской реконструктивной, полутрубчатой пластины и фиксирующих винтов; и модели винтов диаметром 2 мм, 3,5 мм и 4,5 мм, длиной 4 мм, 13 мм и 18 мм, которые построены соответственно их реальным размерам. Количество элементов в модели варьировало от 21351 до 51157, узлов — от 37763 до 82186, размеры элементов — от 4,98 мм до 0,2 мм в зависимости от величины, характера, особенностей объекта моделирования и его целей. Наименьший размер КЭ и наибольшее количество узлов использовали при моделировании винта и его соединения с костью. При необходимости в участках, где предполагалось наличие концентрации напряжений, в зонах истончения кортикальной пластины и на участках со сложной геометрией прибегали к сгущению сетки.

Проводили исследование на растяжение, сжатие (продольная устойчивость, продольный изгиб, продольная деформация) и кручение, а также в условиях сложного нагружения (растяжение с изгибом). Кости, испытывающие сжатие, под воздействием нагрузки могут получить продольный изгиб, поэтому выполняли проверку модели кости на устойчивость. Задавали следующие граничные условия. С одного свободного торца кости устанавливали жесткую заделку по поверхности сечения. Перемещение по всем плоскостям было исключено, а с другого торца прикладывали равномерное давление по плоскости сечения или крутящий момент.

На третьем этапе прилагали нагрузку к модели кости. В зависимости от вида модели и задачи исследования статическая физиологическая нагрузка на кость была равной 981 Н, 800 Н, 400 Н при растяжении–сжатии, а при кручении — всегда 0,1 Нм. Величина прилагаемой нагрузки 981 Н соответствует весу среднестатистического мужчины. Нагрузку 400 Н применяли для облегчения расчетов, более точного определения изменения границ полей напряжения, значений максимального напряжения.

При взаимодействии кости с металлической накладкой усилия от кости к накладке передаются винтами. Поскольку накладка препятствует продольной деформации кости при нагружении, то на винт действуют в основном срезывающие силы. Кроме того, наличие кривизны кости обуславливает возникновение изгибных напряжений при растяжении и осевых нагрузок на винт. По этой причине изучены факторы, влияющие на прочность фиксации винта в кости при осевой и касательной нагрузках на головку винта, проведенного вне пластины. При исследовании напряжения в контактных парах винт – кортикальная кость (в области сопряжения винт – кость ) закрепление кости осуществляли с двух торцов, применяли жесткую заделку. Величина тангенциальной нагрузки составила 100 Н, а осевой нагрузки — 50 Н, 100 Н, 150 Н. В качестве дополнительного критерия использовали величины напряжений в пластине и винтах.

Выполняли качественную и количественную оценку полей напряжений неповрежденной кости после формирования вырезов различных форм и размеров с кривизной в различных плоскостях без компенсации дефекта и после профилактического укрепления кости. Определяли величину и зону максимальной концентрации напряжений в различных отделах выреза диафизарной части кости, пластины и винтов, а также изменение площади зоны концентрации максимального напряжения при сжатии– растяжении и кручении в зависимости от формы, глубины выреза, изгиба кости в двух плоскостях и способов ее профилактического укрепления металлической пластиной на винтах.

В качестве критерия оценки эффективности пластины-фиксатора выбраны величины напряжения в костной ткани. Использование КЭМ позволило определить и описать зоны концентрации локальных напряжений, исследовать их количественные значения и градиенты в глубине и на поверхности кости.

РЕЗУЛЬТАТЫ

НДС модели кости без выреза и кривизны характеризовалось плавным распределением своих параметров по поверхности модели, отсутствием их резких перепадов. Такая модель кости не имела участков концентрации напряжения при растяжении и сжатии. Напряжения при растяжении распределялись равномерно, их значения были минимальными из всех рассмотренных расчетных случаев. При растяжении модели кости с кривизной в вертикальной плоскости пиковые напряжения определяли в области межкостного края, а при наличии изгиба в горизонтальной плоскости — переднего края кости. Присутствие кривизны кости в двух плоскостях в условиях растяжения обуславливало возникновение изгибных напряжений также в двух плоскостях (рис. 1). В этих случаях участки пиковых напряжений имелись в области межкостного и заднего краев лучевой кости. Участок повышенного уровня напряжений при кручении моделей кости с кривизной располагался по переднему краю и передней поверхности кости.

Наибольшее напряжение модель кости с кривизной и вырезом испытывала в области выреза при всех видах нагружения. Наблюдали области концентраций напряжений в зонах с изменением геометрии. Формирование выреза вызывало концентрацию напряжения в углах треугольного и прямоугольного вырезов, а также повышенный уровень напряжений по всей горизонтальной части прямоугольного выреза и передней поверхности кости при всех видах нагрузок. По мере увеличения глубины выреза пиковые напряжения и площадь их распространения также увеличивались как при растяжении, так и при кручении при всех видах кривизны кости. Максимальные напряжения при растяжении, сжатии и кручении, как и следовало ожидать, наблюдали в месте, где поперечное сечение модели кости было минимальным. При наличии кривизны кости и выреза распределение напряжения было также неоднородным. При растяжении и наличии изгиба кости в горизонтальной плоскости максимальное напряжение отмечали по переднему краю выреза любой формы.

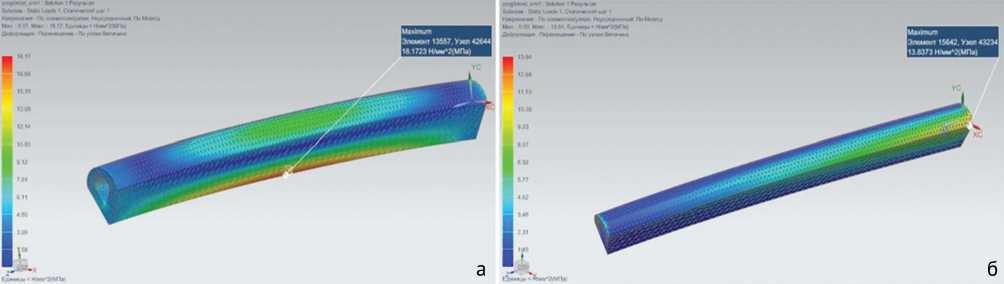
Рис. 1. Распределение эквивалентных напряжений по Мизесу в кости без выреза с начальной погибью в двух направлениях: а — при растяжении; б — при кручении

При изгибе кости в вертикальной плоскости максимальное напряжение отмечали в области межкостного края при вырезе любой формы. В случае изгиба модели кости в двух плоскостях отмечены выраженные зоны концентрации напряжения в следующих областях:

• —    межкостный край кости в зоне максимального прогиба;

• —    в углу треугольного выреза по заднему краю (при растяжении–сжатии);

• —    по всей плоскости или по заднему краю продольной части прямоугольного выреза в зависимости от его глубины (рис. 2, 3).

Рис. 2. Распределение эквивалентных напряжений по Мизесу в кости с прямоугольным вырезом и с начальной погибью в двух направлениях: а — при растяжении; б — при кручении

Рис. 3. Распределение эквивалентных напряжений по Мизесу в кости с треугольным вырезом и с начальной погибью в двух направлениях: а — при растяжении; б — при кручении

При кручении концентрацию напряжения отмечали в области выреза: треугольного — в углу выреза, прямоугольного — по всей плоскости или по краям продольной части выреза в зависимости от его глубины. Зона наибольших напряжений треугольного выреза по длине кости оказалась существенно меньше, чем прямоугольного как при растяжении, так и кручении.

В результате расчетов выявлено, что конструктивная форма выреза, при котором обеспечивается наибольшее восприятие нагрузки при растяжении и кручении, имеет треугольную форму глубиной h 0 /H = 0,16 (где h 0 — глубина выреза, H — высота сечения кости без выреза). По мере увеличения глубины выреза кости с кривизной до h 0 /H = 0,33 пиковые значения максимальных напряжений увеличивались при всех формах выреза.

Таблица 1

Эквивалентные напряжения по Мизесу в костях разной формы при растяжении и кручении

Виды нагружения	Напряжения по Мизесу в зависимости от формы кости, МПа
	без выреза и начальной погиби	без выреза с начальной погибью	с треугольным вырезом и начальной погибью	с прямоугольным вырезом и начальной погибью
Растяжение, F = 400 Н	6,28	18,17	64,82	82,45
Кручение, M = 0,1 Н·м	12,93	13,84	37,17	76,70

Как следует из табл. 1, наименьшие напряжения испытывает кость без выреза и первоначальной кривизны. Наличие первоначальной кривизны увеличивает напряжение в 2,89 раз при растяжении и всего в 1,1 раза при кручении по сравнению с моделью кости без погиби. По полученным результатам можно сделать вывод, что самые большие напряжения выявлены при наличии прямоугольного выреза и начальной погиби кости в двух направлениях при всех видах нагрузок. При одинаковой глубине выреза треугольная форма более предпочтительна, чем прямоугольная, так как при идентичной нагрузке возникает меньший уровень напряжений. Напряжение треугольного выреза составляет 78,6 % от напряжения прямоугольного выреза при растяжении и 48,5 % при кручении, то есть треугольный вырез снижает уровень напряжений на 21,4 % при растяжении и 51,5 % при кручении.

Наличие кривизны кости вызывает увеличение уровня напряжений при растяжении в ее модели без повреждения в 2,89 раз за счет появления напряжений от изгиба, в условиях сочетания ее с треугольным вырезом — в 10,32 раз, с прямоугольным вырезом — в 13,13 раз по сравнению с моделью без кривизны и выреза. Кривизна кости увеличивает уровень напряжения при кручении в 1,1 раза при отсутствии повреждения, в 2,88 раза при треугольном вырезе, в 5,93 раз при прямоугольном вырезе (табл. 1). Напряжения, вызванные наличием выреза и кривизны кости, суммируют.

Результаты анализа поведения модели кости под сжимающей нагрузкой показали, что модель при нагрузке 981 Н не может работать без потери устойчивости при любом виде искусственного выреза, поскольку критические напряжения для первой формы потери устойчивости были на порядок ниже выявленных максимальных напряжений при данной нагрузке в отличие от модели без выреза. Модель с треугольным вырезом имеет больший запас прочности по продольной устойчивости (в 1,18 раз) по сравнению с моделью с прямоугольным вырезом (табл. 2).

Таблица 2

Напряжения, действующие в образцах с различными вырезами при решении задачи продольной устойчивости

Форма кости	Напряжения σ , МПа
	σ max	σ кр для первой формы потери устойчивости
Без выреза	31,76	54,18
Прямоугольный вырез	47,60	39,96
Треугольный вырез	59,23	46,99

Как показывает изучение литературных данных, чаще всего на практике для остеосинтеза используют узкие пластины. В связи с этим и фактом, что кость с треугольным вырезом и пластиной оказалась по большинству параметров прочнее кости с прямоугольным вырезом и пластиной, в дальнейшем исследовали только вариант укрепления кости с треугольным вырезом. На модели кости с вырезом и пластиной при всех видах нагружения, выреза и погиби напряжение было больше в области дефекта и на пластине в проекции дефекта. Концентраторы напряжений возникали в местах изменения геометрии, а также в узлах контакта деталей (рис. 4).

Рис. 4. Распределение эквивалентного напряжения по Мизесу в кости с треугольным вырезом при сжатии (четыре винта, толщина пластины 2 мм): а — общее распределение в модели, б — распределение в кости

Напряжения по длине пластины между винтами в районе выреза были распределены практически равномерно по ширине пластины и сосредоточены между винтами, а за пределами винтов в консольных частях равны нулю. Наибольшие напряжения кости отмечали в ближайших к вырезу винтах. При сквозном проведении винтов также выделяли зоны повышенного напряжения в области выхода винтов, более выраженные в винтах, находящихся рядом с дефектом.

Критерием оценки эффективности пластины считали снижение напряжения в кости с накладкой по отношению к напряжению в кости без накладки. На моделях с прямоугольным вырезом, замещенным идентичным по форме и размерам кортикальной вставкой, фиксированной винтами с укреплением кости пластиной, при растяжении максимальное напряжение отмечали в пластине на уровне угла выреза. Зону максимального напряжения в кости определяли в области межкостного края на этом же уровне. При фиксации вставки только винтами очаги максимального напряжения в кости отмечали в углах выреза и в области межкостного края на этих же уровнях. На данной модели применение пластины уменьшило максимальное напряжение в кости в 2,21 раза.

При растяжении модели уровень напряжения в кости зависит и от толщины пластины, и от количества винтов (рис. 5). Выявлено, что в этих условиях при использовании пластины толщиной 1 мм напряжения превышают свои допустимые значения. По сравнению с этим расчетным случаем в модели кости с установленной пластиной толщиной 2 мм наблюдали спад напряжений. Также отмечена прямая зависимость спада напряжения от количества винтов. Допускаемый уровень напряжения достигается при моделировании пластины толщиной 2 мм на четырех винтах при монокортикальном проведении. Установлено, что при использовании пластины толщиной 2 мм условие прочности выполняется. Между значениями напряжений и толщиной пластины наблюдается обратная зависимость. Обнаружено, что при использовании пластины толщиной 3 мм условие прочности также выполняется. В модели кости с установленной пластиной толщиной 3 мм наблюдали спад напряжений в сравнении с моделью с пластиной толщиной 2 мм.

Можно сделать вывод, что использование пластины толщиной 3 мм является самым эффективным с точки зрения максимальных напряжений. В целях экономии материала допустимо использование пластины толщиной 2 мм, так как при ее расчете полученные эквивалентные напряжения в кости не превышают предела прочности и незначительно отличаются от таковых в модели кости с пластиной толщиной 3 мм. Напряжения в пластине толщиной 2 мм при использовании четырех винтов мало отличаются от напряжения при применении шести винтов. По этой причине достаточным является применение пластины толщиной 2 мм на четырех винтах, так как использование пластин с большим количеством винтов в клинических условиях является более травматичным. Наименьшее напряжение в кости отмечено при использовании пластины толщиной 3 мм на шести фиксирующих винтах, поэтому такая система фиксации желательна при наличии выраженного изгиба и увеличении глубины выреза более половины кости, когда напряжение в ней резко увеличивается.

Как показывает анализ графиков, при кручении увеличение количества винтов практически не влияет на напряжение в кости (рис. 5). Увеличение толщины пластины уменьшает напряжение в кости при всех видах нагрузок. В самой пластине напряжение также уменьшается при увеличении ее толщины и при ее значении 3 мм мало зависит от количества фиксирующих винтов.

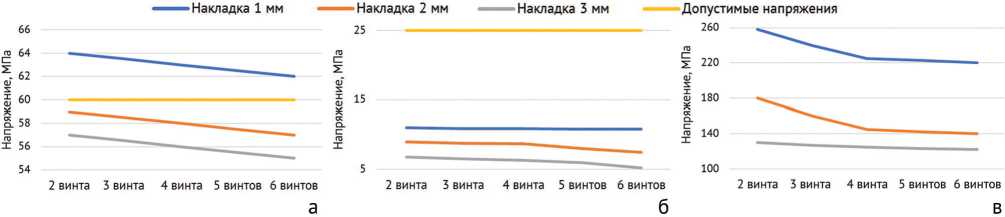
Рис. 5. Графики зависимости эквивалентных напряжений от толщины пластины и количества фиксирующих винтов: а — в кости при растяжении; б — в кости при кручении; в — в накладке при растяжении

Также изучено распределение напряжений в системе пластина – кость – винт на модели кости с треугольным вырезом и пластиной на двух винтах при различной ее толщине в условиях растяжения (табл. 3) и кручения (табл. 4). По результатам выполненного расчета при растяжении и кручении можно сделать вывод, что зависимость напряжения в пластине, кости и винте от толщины пластины носит линейный характер. С увеличением толщины пластины напряжения уменьшаются в каждом элементе нашей рабочей модели пластина – кость – винт . Наибольшая концентрация отмечена в пластине, что свидетельствует о том, что она забирает на себя большую часть нагрузок, возникающих при растяжении и кручении кости. Самые малые напряжения выявляются на винте.

Таблица 3

Значения эквивалентных напряжений по Мизесу в зависимости от толщины пластины при растяжении с нагрузкой F = 980 Н

Толщина пластины, мм	Напряжение σ , МПа
	в пластине	в кости	в винте
2,0	154,69	121,48	46,00
2,5	126,16	111,34	30,20
3,0	124, 93	110,49	23,89

Таблица 4

Значения эквивалентных напряжений по Мизесу в зависимости от толщины пластины при кручении с нагрузкой М = 0,1Н·м

Толщина пластины, мм	Напряжение σ , МПа
	в пластине	в кости	в винте
2,0	58,32	19,43	13,07
2,5	55,62	16,80	12,70
3,0	52,88	14,77	10,31

При всех видах нагрузок основную роль играет пластина, разгружающая костную ткань. Винты принимают на себя напряжение в кости и передают его на пластину. При любой толщине пластины напряжения в кости не превышают пределов прочности при растяжении, а при кручении — даже допускаемых напряжений. Это обусловлено тем, что пластина снижает угол закручивания за счет своей жесткости, уменьшая тем самым уровень напряжения в кости в большей степени, чем при растяжении.

Расчет моделей костей на продольную устойчивость проводили для искусственных повреждений прямоугольной и треугольной формы с относительной глубиной выреза h 0 /H = 0,33, с погибью f х и f z , с погружением шести винтов, фиксирующих к кости полутрубчатую пластину толщиной 2 мм, на глубину 13 мм. Анализ результатов влияния укрепления кости пластиной на продольную устойчивость представлен в табл. 5.

Таблица 5

Разрушающие и критические нагрузки, действующие на кости с вырезами

Показатели прочности		Величины нагрузок
		без выреза	прямоугольный вырез	треугольный вырез	прямоугольный вырез с пластиной	треугольный вырез с пластиной
Растяжение	σ р , МПа	—	47,60	44,44	41,95	39,68
	н раз ,	—	2473	2649	2806	2967
Сжатие	σ р , МПа	31,76	47,60	44,44	30,61	30,51
	Р раз , Н	3706	2473	2649	3846	3858
	К = Р кр /Р р	–1,219	–3,544	–4,057	–5,128	–5,425
	Р кр , Н	4238	3477	3980	5030	5322

Расчетная нагрузка Р р принята равной 981 Н, разрушающая нагрузка Р раз вычислена при достижении предела прочности σ в = 120 МПа. Разрушающая нагрузка кости без выреза превышает расчетную нагрузку в 3,78 раза, это — коэффициент запаса по нагрузке. Расчеты показали, что критическая нагрузка кости с дефектом в 1,4–1,5 раза выше, чем разрушающая нагрузка. Разрушение кости будет происходить от сжатия, а не от потери устойчивости. Пластина увеличивает критическую нагрузку в 1,45 раза для прямоугольного выреза и в 1,34 раза для треугольного выреза, а также увеличивает разрушающую нагрузку для прямоугольного выреза в 1,56 раза, а для треугольного выреза в 1,46 раза. Критические и максимальные напряжения в кости представлены в табл. 6.

Таблица 6

Критические и максимальные напряжения, действующие в образцах с различной формой выреза и полутрубчатыми пластинами при сжатии

Характер выреза кости с пластиной	Напряжение, МПа
	максимальное σ max	критическое σ кр 1
Прямоугольный вырез	30,61	58,08
Треугольный вырез	30,51	61,55

Анализ данных показывает, что модель кости с металлической пластиной при расчетной нагрузке 981 Н может работать без потери устойчивости при любом виде искусственного выреза, поскольку критические напряжения для первой формы потери устойчивости оказались вдвое выше выявленных максимальных напряжений при расчетной нагрузке.

Проведен сравнительный анализ эффективности влияния на напряжение в модели кости с различными вырезами с относительной глубиной h 0 /H = 0,33, с погибью f х и f z , плоской узкой и полутрубчатой пластин толщиной 2 мм и погружением шести фиксирующих винтов на глубину 13 мм (табл. 7).

Таблица 7

Сравнение максимальных и критических напряжений в кости при различной форме выреза и способах фиксации

Формы выреза	σ max при растяжении, МПа		τ max при кручении, МПа		Критическое напряжение 1-й формы потери устойчивости σ кр 1 , МПа
	плоская пластина	полутрубчатая пластина	плоская пластина	полутрубчатая пластина	без пластины и выреза	полутрубчатая пластина
Прямоугольный	36,47	30,59	5,914	1,505	39,96	58,08
Треугольный	47,03	30,53	5,51	1,55	46,99	61,55

Полутрубчатая пластина по сравнению с плоской узкой компенсирующей накладкой шириной 10 мм снижает уровень напряжений при растяжении в 1,2 раза для искусственного выреза прямоугольного сечения, в 1,5 для искусственного выреза треугольного сечения; при кручении, — в 3,9 раза для прямоугольного сечения выреза, в 3,5 раза для треугольного сечения искусственного выреза.

При растяжении значения напряжений соответствуют значениям целой кости, составляющей 31,59 МПа, а при кручении значения близки и составляют 60–70 % работы целой кости, равной 0,757 МПа. Кроме того, отмечено увеличение критических напряжений в 1,3–1,5 раза при использовании полутрубчатой пластины по сравнению с моделью кости без кривизны и выреза. По критерию устойчивости предлагаемая накладка имеет значения выше, чем для целой кости, равной 54,18 МПа. Таким образом, выявлено, что полутрубчатая пластина имеет лучшее восприятие нагрузки, как при кручении, так и при растяжении, чем плоская пластина шириной 10 мм. С увеличением толщины пластины увеличивается восприятие нагрузки. При растяжении наилучшим образом себя повели образцы с погружением винта на 4 мм, при кручении образцы с погружением в 4 мм и 13 мм вели себя почти одинаково. Образец со сквозным погружением винта привел к повышению напряжения в кости в области проведения винтов.

Анализ НДС модели пары винт – кость проводили для выявления механизмов возникновения нестабильности винта, приводящих к развитию осложнений остеосинтеза. Изучение полей напряжения при взаимодействии винта с костью при тангенциальной и осевой нагрузке показало, что наибольшая концентрация напряжений в винте возникала около его головки, к которой прикладывается срезывающая сила от пластины (рис. 6). В кости наибольшая концентрация напряжений возникала в районе максимальных напряжений в винте, а именно на входе винта в кость.

Рис. 6. Распределение эквивалентных напряжений по Мизесу в винте и кости при касательной нагрузке 150 Н: а — распределение напряжений в области контакта винта и кости; б — распределение напряжений в кости; в — распределение напряжений в винте

Количественные параметры механических напряжений при касательных нагрузках на винт представлены в табл. 8, 9, 10. По приведенным результатам видно, что зависимость напряжений от приложенной нагрузки носит линейный характер (табл. 8). С уменьшением толщины слоя кости напряжения увеличиваются. При толщине 2,8 мм при нагрузке 150 Н напряжение в кости превысило даже предел прочности в 130 МПа.

Коротким считали винт, проходящий через один кортикальный слой, длинным — через оба. С увеличением длины винта напряжение в кости увеличивалось, а при нагрузке 150 Н превышало предел прочности кости (табл. 9). Толщину кортикального слоя кости при этом принимали равной 3,14 мм.

Таблица 8

Значения эквивалентных напряжений в кости и винте в зависимости от толщины кортикального слоя кости при касательных нагрузках

Нагрузка F, Н	Напряжения в кости σ , МПа		Напряжения в винте σ , МПа
	t = 3,14 мм	t = 2,8 мм	t = 3,14 мм	t = 2,8 мм
50	31,13	46,52	52,41	109,92
100	72,26	93,04	104,82	219,84
150	108,39	139,1	157,23	330,49

Примечание : t — толщина кортикального слоя кости.

Таблица 9

Значения эквивалентных напряжений в кости и винте в зависимости от длины винта при касательных нагрузках

Нагрузка F, Н	Напряжения в кости σ , МПа		Напряжения в винте σ , МПа
	короткий винт	длинный винт	короткий винт	длинный винт
50	31,13	42,81	52,41	126,59
100	72,26	85,63	104,82	253,18
150	108,39	128,44	157,23	379,77

Таблица 10

Значения эквивалентных напряжений в кости и винте в зависимости от диаметра винта при касательных нагрузках

Нагрузка F, Н	Напряжения в кости σ , МПа		Напряжения в винте σ , МПа
	d = 3,5 мм	d = 4,5 мм	d = 3,5 мм	d = 4,5 мм
50	31,13	20,51	52,41	24,27
100	72,26	41,02	104,82	48,54
150	108,39	61,53	157,23	72,81

Как следует из полученных данных, зависимость напряжений от приложенной нагрузки для винтов разного диаметра также носит линейный характер. С увеличением диаметра винта напряжение в кости уменьшается, но и при меньшем диаметре винта напряжение не превышает предела прочности кости (табл. 10). Однако сдвиговая нагрузка на винт, равная 50 Н, при большинстве его параметров и значений толщины кортикального слоя уже приводит к увеличению касательных напряжений в кости, превышающих допускаемые значения, за исключением винта диаметром 4,5 мм. При больших нагрузках во всех случаях отмечается превышение допускаемых значений.

Таким образом, при различных параметрах винта (диаметр и длина) и кости (толщина) зависимость напряжений от приложенной касательной нагрузки носит линейный характер. Это позволяет прогнозировать уровень напряжений при действии подобной нагрузки. Характер распределения напряжений был одинаковым при всех значениях нагрузок. Как показывает анализ результатов, возникающие напряжения в кости не превышают или достигают предела прочности при различных параметрах винта (длине и диаметра), но превышают предел прочности при уменьшении толщины кортикального слоя и увеличения длины винта при нагрузке 150 Н. Кроме того, с увеличением длины винта возрастают касательные напряжения и в винте, и в кости.

При осевой нагрузке наибольшую концентрацию напряжений в винте отмечали в области трех первых витков резьбы, а в кости — в области входа в нее винта. Максимальные напряжения в кости также линейно зависели от приложенной осевой нагрузки на винт при его закручивании. При нагрузке в 150 Н получено максимальное эквивалентное напряжение в кости 88,4МПа, что превышает допускаемые значения напряжения в кости, вследствие чего не исключается возможность разрушения и резорбции костной ткани в области контакта с элементами связи пластины с костью и нарушения стабильности остеосинтеза (рис. 7). Из графика также следует, что осевая нагрузка на винт, превышающая 100 Н, вызывает в кости максимальные нормальные напряжения, превышающие их допускаемые значения.

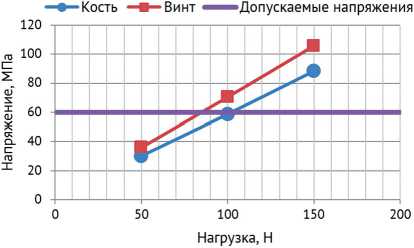
Рис. 7. График зависимости эквивалентного напряжения в кости и винте от прикладываемой осевой нагрузки

Максимальные напряжения в кости также линейно зависят от приложенной нагрузки. Это позволяет распространить полученные результаты на другие дей- ствующие нагрузки, а также прогнозировать уровень напряжений при известной нагрузке с целью избегания нежелательного разрушения (локальных микроразрушений) кортикального слоя вокруг отверстий и срыва резьбы вследствие чрезмерной затяжки винта.

Таким образом, НДС модели кости с вырезом зависит от многих факторов, характера нагрузок, способов компенсации дефекта, которые целесообразно учитывать в клинической практике для разработки мероприятий по увеличению остаточной прочности донорской лучевой кости.

ОБСУЖДЕНИЕ

В исследовании были поставлены важные в практическом отношении вопросы, — как влияют формирование выреза, наличие кривизны кости в двух плоскостях на НДС модели кости, какие подходы и способы обеспечивают увеличение остаточной прочности кости и допускаемый уровень напряжения в ней.

В последние годы в мировой литературе наблюдается рост публикаций, посвященных применению метода конечных элементов в травматологии и ортопедии, в том числе и для моделирования переломов лучевой кости. Согласно опубликованным данным, метод оказался очень информативным при изучении прочности кости [16, 17, 25], его можно применять для прогнозирования возникновения и профилактики переломов изначально целой лучевой кости [16, 17]. Установлено, что построенные с использованием конечных элементов скелетные модели обеспечивают неинвазивную оценку прочности и стабильности имплантата [20]. Причем авторы для построения КЭ модели применяли данные компьютерной томографии костей экспериментальных животных и искусственных костей. Отмечена высокая степень корреляции параметров КЭ модели и кадаверной кости [16, 17, 19], что подтверждают и наши исследования, проведенные на анатомических препаратах человека и моделях на их базе. Опубликованы исследования по КЭ моделированию кости с краевым дефектом, при котором целостность одной из кортикальных пластинок сохраняется [22]. Работ по КЭ моделированию лучевой кости с подобным дефектом и компенсирующими элементами на основе анатомических препаратов человеческой кости с применением теории изгиба балок и поперечных сечений мы не нашли.

Формирование выреза в модели диафиза лучевой кости вызывает значительное увеличение показателей максимального нормального напряжения по сравнению с неповрежденной костью, что можно объяснить уменьшением площади поперечного сечения и его геометрического момента инерции в области выреза. Увеличение напряжений свидетельствует о снижении прочности и возрастании вероятности перелома в реальных условиях.

Противоречивым остается мнение хирургов о влиянии формы выреза на остаточную прочность кости. Некоторые авторы утверждают, что формирование челночного (радиусного, ладьевидного) или килевидного (треугольного) выреза при формировании и заборе трансплантата является достаточным для надежной профилактики перелома лучевой кости, без применения профилактического остеосинтеза [26]. В то же время другая группа специалистов не видит в этом необходимости, считая, что это лишь позволяет предупредить превышение глубины выреза и улучшить доступ и обзор в области операции [8, 27, 28]. Масштабы увеличения напряжения в зависимости от скашивания плоскости остеотомии и увеличения глубины выреза исследованы недостаточно, а приводимые данные противоречивы [28, 29, 30]. Так, согласно результатам одних авторов, формирование подобного выреза сопровождается минимальным эффектом и приводит к увеличению прочности кости при кручении всего лишь на 5 % [28, 29], в то время как другие отмечают существенное положительное влияние формы остеотомии на прочность при изгибе и кручении [30]. Полученные нами данные совпадают с результатами КЭМ других авторов, согласно которым пиковые значения напряжения при четырехточечном изгибе и кручении были на 24–30 % выше при прямоугольной остеотомии, чем при скошенной [30]. Такой результат объясняется тем, что прямоугольный вырез имеет два концентратора напряжения в углах дефекта, а треугольный — один, причем с меньшим коэффициентом концентрации напряжения. Теоретически радиусный (ладьевидный, челночный) вырез будет иметь еще меньшую концентрацию напряжений за счет скругления (плавного изменения формы) выреза в наиболее узкой части сохранившейся кости. Однако при этом нормальное напряжение в кости оказывается все же выше допускаемых значений, в связи с чем формирование даже треугольного или радиусного выреза необходимо сочетать с другими способами укрепления [28]. Кроме того, увеличение глубины выреза приводит к непропорциональному увеличению напряжения в кости, особенно при кручении, независимо от формы выреза [30]. Значение изгиба кости в генезе НДС до настоящего времени остается практически неизученным. Нами получены данные, согласно которым наличие кривизны кости приводит к увеличению нормальных напряжения при растяжении почти в три раза по сравнению с моделью кости без кривизны. Увеличение напряжения растяжения–сжатия при наличии изгиба кости можно объяснить возникновением продольного изгибающего момента из-за возникновения эксцентриситета сил, выраженность которого зависит от величины изгиба, что было доказано методом математического модели- рования [31] . Согласно полученным данным, можно констатировать, что наличие выреза в сочетании с изгибом кости еще более существенно ослабляет ее в соответствии с принципом суперпозиции сил, на основании которого нормальные напряжения растяжения и изгибные напряжения, обусловленные наличием изгиба и дефекта кости, суммируют. Это подтверждается также изучением распределения полей напряжения.

В настоящее время остается неизученной продольная устойчивость кости с вырезом. В реальных условиях этот вид воздействия может возникнуть в случае осевой нагрузки (сжатия) на предплечье при падении или ударе. По нашему мнению, потеря продольной устойчивости кости с вырезом происходит за счет уменьшения геометрического момента инерции сечения и наличия первоначальной кривизны кости, что приводит к эксцентриситету сжимающей и растягивающей силы, то есть к внецентренному растяжению и сжатию. Причем, само наличие выреза также приводит к эксцентриситету силы и возникновению изгибающего момента. Больший запас прочности кости с треугольным вырезом по продольной устойчивости по сравнению с прямоугольным вырезом объясняется ослаблением его сечения на большем протяжении, поэтому момент инерции сечения у кости в месте прямоугольного выреза оказывается меньше.

В литературе имеются сведения об увеличении прочности лучевой кости с краевым дефектом при фиксации ее накостной мостовидной пластиной в условиях изгиба и кручения [6, 18, 21, 28]. Опубликованы работы по изучению влияния плоских прямых и Т-образных пластин на напряженно-деформированное состояние КЭ модели кости с краевым вырезом [22]. Однако механизмы изменения максимальных напряжений в кости при использовании других, в том числе полутрубчатых пластин, до настоящего времени не исследовано. На современном этапе развития реконструктивной хирургии также окончательно не определены размеры, расположение пластины, количество, размеры фиксирующих винтов и характер их проведения, нет данных по сравнительному анализу эффективности вариантов профилактического остеосинтеза кости с краевым дефектом с использованием МКЭ при различных видах нагружения [8, 21]. Количественный анализ полей напряжения модели с пластиной показал, что фиксация пластиной толщиной 2 мм на четырех винтах (по два с каждой стороны дефекта) диаметром 2,0 мм, проведенных бикортикально, является достаточной для снижения уровня напряжений в кости, так как они в этом случае не превышают допускаемые, хотя и приближаются к ним. При большей толщине пластины и большем количестве винтов уровень напряжений в кости уменьшается незначительно. Кроме того, увеличение количества винтов и, соответственно, длины пластины в клинике приводит к увеличению продолжительности, травматичности вмешательства и риска нарушения кровообращения кости. Эти результаты можно объяснить тем, что при простом растяжении и сжатии мерой жесткости пластины является площадь поперечного сечения. Увеличение толщины пластины с 1 мм до 2 мм увеличивает площадь поперечного сечения, а значит и жесткость в два раза, а с 2 мм до 3 мм всего на треть. По этой причине целесообразно применение пластины толщиной 2 мм, так как напряжение в кости уменьшается незначительно по сравнению с пластиной толщиной 3 мм. Превышение допустимых напряжений кости в модели с пластиной толщиной 1 мм можно объяснить недостаточной жесткостью самой пластины и высоким напряжением в ней, что приводит к увеличению напряжения и в кости. Необходимое количество фиксирующих винтов может быть обосновано также путем качественного анализа полей напряжения модели. Изучение влияния количества фиксирующих винтов, их расположения и толщины пластины на характер распределения напряжений в различных элементах модели показало, что основную нагрузку при моделировании профилактического укрепления кости пластиной несут фиксирующая пластина и сохранившийся кортикальный слой лучевой кости в области выреза. Такие участки кости имеют уменьшенную несущую способность, и нагрузка с них передаётся на подкрепляющую пластину посредством винтов за пределы выреза, тем самым увеличивая прочность в районе дефекта. При условии правильной установки винтов, нагрузка между ними при растяжении–сжатии зависит от их количества: чем больше винтов, тем меньше оказывается напряжение в винтах и материале кости. В случае расположения винтов в один продольный ряд и незначительном трении между пластиной и материалом кости нагрузка, приходящаяся на каждый винт, будет зависеть от расстояния между винтами и их удаленности от дефекта. Наличие трения между пластиной и костью теоретически уменьшит нагрузку на винты, так как частично она будет восприниматься поверхностями трения. Однако при гладкой контактной поверхности подкрепляющей пластины это уменьшение может быть несущественным. При этом наиболее нагруженными оказались участки подкрепляющей пластины в зоне выреза и ближайшие к дефекту винты за счет расположения их рядом с ослабленной частью кости. Это можно объяснить нахождением их в зоне действия высоких напряжений из-за расположения рядом с частью кости с уменьшенным сечением и соответственно с меньшей жесткостью, испытывающей наибольшие деформации (продольные и угловые перемещения) и напряжения вместе с пластиной в области выреза по сравнению с неповрежденными участками. В следующей от дефекта паре винтов напряжения будут ниже, а при наличии третьей пары винтов еще ниже, что согласуется с результатами других исследований, проведенных с применением МКЭ [22]. При трех и более винтах основную нагрузку воспринимают первые два винта, последующие воспринимают значительно меньшие нагрузки и поэтому малоэффективны. В максимальной степени напряжение ослабевало в области двух концевых винтов. Подобное распределение напряжений в винтах при растяжении–сжатии расчетной модели можно объяснить не только наличием ослабленного участка кости, но и несовпадения осей кости и подкрепляющей пластины и возникновением эксцентриситета сил, приводящего к изгибу и повороту кости. Полученные данные согласуются с результатами других исследований, проведенных с применением МКЭ, по анализу распределения напряжений между винтами на модели фиксации перелома диафиза трубчатой кости с использованием динамической компрессионной пластины (DCP) и фиксирующей компрессионной пластины с угловой стабильностью (LCP), а также при изучении отдаленных результатов накостного остеосинтеза длинных трубчатых костей по рентгенограммам [18, 22].

В условиях скручивающих нагрузок напряжение в кости оказывается меньше допускаемых даже для пластины толщиной 1 мм. Это объясняется тем, что пластина значительно снижает угол закручивания за счет своей жесткости, поэтому количество винтов и ее толщина мало влияет на величину напряжений. Однако в случае использования плоских накладок при креплении только одним винтом с каждой стороны одиночный винт не препятствует повороту и возможному сдвигу пластины при нагружении, что исключается при фиксации двумя винтами с каждой стороны дефекта или применения полутрубчатой пластины. Максимальное напряжение сдвига, возникающее в плоскости пластины, отмечается также в ближайших к дефекту винтах. Кроме того, при увеличении количества винтов еще в большей степени уменьшается угол закручивания за счет увеличения жесткости соединения. При увеличении толщины пластины напряжение в ней уменьшается и мало зависит от количества винтов, что можно объяснить увеличением площади поперечного сечения модели и прочности (жесткости за счет высокого модуля упругости металла) соединения. Однако крепление меньшим количеством винтов (по одному с каждой стороны) с точки зрения работы на кручение малоэффективно даже при установке подобных пластин. При закручивании кости характер распределения нагрузки между винтами оказывается иным, и можно предположить, что при креплении уже двумя парами винтов жесткость получившегося сечения на кручение достаточна, так как углы закручивания малы и увеличение количества винтов незначительно влияет на эти параметры. С учетом данных фактов, можно предположить, что фиксация узкой пластиной толщиной 2 мм на четырех винтах диаметром 4 мм обеспечивает достаточную прочность и при касательных нагрузках на расчетную модель.

Анализ распределения напряжений в различных элементах нашей модели кость – винт – пластина показал, что при растяжении–сжатии и кручении кости наибольшие напряжения получены в пластине, наименьшие — в винтах. Данный результат можно объяснить тем, что в винтах действуют преимущественно касательные напряжения (от среза), которые, как правило, меньше нормальных. В пластине в зоне контакта с винтом действуют преимущественно нормальные напряжения смятия, а в кости — как нормальные, так и касательные. По мере увеличения толщины пластины линейно уменьшаются напряжения во всех элементах конструкции. Однако в клинике увеличение толщины пластины приводит к увеличению жесткости фиксации, что вызывает «стресс-экранирующий» эффект и ослабление кости [6, 32, 33], а также выступание пластины над мягкими тканями или даже ее пролабирование [33]. Кроме того, это сопровождается увеличением травматичности вмешательства, а также риска повреждения мышц, нервов, сосудов, нарушения кровообращения кости и развития инфекционных осложнений [34]. Благодаря более низкому профилю пластины, в реальных условиях она будет занимать минимальный объем в тканях, что облегчит их ушивание над пластиной без натяжения краев раны. Кроме того, такие пластины могут обеспечить потенциальное преимущество перед пластиной толщиной 3,5 мм для ускорения заживления переломов за счёт меньшего экранирования напряжения, позволяя равномерно распределять силы по всей своей длине. Экспериментальными исследованиями на композитной анатомической модели кости предплечья установлена пластическая деформация низкопрофильной пластины без ее разрушения, благодаря ее гибкости, несмотря на чрезмерные нагрузки, что потенциально предотвращает повторный перелом, отмечаемый при использовании пластин с повышенной толщиной [33].

Выявленные нами преимущества полутрубчатой пластины перед плоской узкой пластиной можно объяснить тем, что модель кости с пластиной, имеющей форму огибающей цилиндрическую поверхность кости, воспринимает большую нагрузку вследствие увеличенной жесткости соединения в двух направлениях за счет формы металлоконструкции. При этом увеличение толщины пластины также приводит к снижению напряжений во всех элементах системы кость – винт – пластина, так как увеличивается площадь и момент инерции поперечного сечения соединения. Данная пластина по сравнению с узкой прямой пластиной в большей степени снижает уровень напряжения в кости как при растяжении, так и кручении (основном механизме, способствующем перелому, при котором нагрузка на лучевую кость не может быть шунтирована локтевой костью). По критерию продольной устойчивости кость с треугольным вырезом, укрепленная данной пластиной, имеет значения критических напряжений выше, чем у целой кости. Большие значения критического напряжения модели кости с треуголь- ным вырезом, укрепленной данной пластиной, по сравнению с моделью с прямоугольным вырезом и аналогичной пластиной при продольном изгибе и кручении свидетельствуют о целесообразности выполнения треугольного выреза в сочетании с профилактической фиксацией накостной пластиной. Можно предположить, что аналогичные закономерности будут иметь место и при других видах нагрузок. Это согласуется с точкой зрения хирургов о необходимости скашивания углов выреза, а также выполнения его треугольной или ладьевидной формы в сочетании с профилактической фиксацией кости пластиной [8, 22]. Поскольку фиксация пластиной повышает остаточную прочность лучевой кости, становится осуществимым забор большей части поперечного сечения кости, что позволит выполнить реконструкцию большего дефекта без опасности перелома лучевой кости. Согласно литературным данным, без выполнения профилактической фиксации кости может быть осуществлен забор трансплантата толщиной, не превышающей 1/2 диаметра или окружности кости [6, 21].

В литературе имеются также единичные сообщениям об успешной профилактике перелома путем замещения дефекта аутокостной вставкой, фиксированной винтами. По нашим данным, замещение прямоугольного дефекта компенсирующей вставкой без профилактического укрепления пластиной не обеспечивает необходимого уровня снижения напряжения в кости, и высокие значения концентрации напряжения сохраняются в углах выреза на все время консолидации вставки.

Прочность соединения винта и кости является определяющей в обеспечении стабильности остеосинтеза накостной пластиной. Проблема развития нестабильности винтов при металлоостеосинтезе сохраняет свою актуальность. Ослабление винта является наиболее распространенным осложнением при фиксации пластиной. Расшатывание винтов приводит к серьезным осложнениям, ведущим к несостоятельности накостного остеосинтеза и переломам пластины и кости. Однако механизмы, лежащие в основе этого явления, в настоящее время изучены недостаточно. Из всех механизмов ослабления винта наиболее распространенными являются образование микротрещин, растрескивание кости в области проведения винта и ее резорбция, вызванные чрезмерным напряжением в окружающей винт перифокальной кости. В связи с этим предметом дискуссии остается вопрос о параметрах, характере проведения фиксирующих пластину винтов, обеспечивающих необходимую прочность кости. Одни авторы сообщают о преимуществах бикортикального [6, 8], другие — монокортикального проведения винтов [24, 35]. Мы анализировали напряжения и деформации кости и винта в области их соединения друг с другом в зависимости от диаметра, длины винта и толщины кортикального слоя. В большинстве случаев, по данным литературы, при изучении механизмов нестабильности винтов оценивали прочность вырывания или закручивания винта при осевой нагрузке на экспериментальных моделях, изготовленных из различных искусственных (синтетических) материалов, в том числе и в условиях применения накостных пластин [36, 37, 38, 39, 40], а также с использованием метода КЭ [41, 42, 43]. Как показали результаты нашего исследования, при чистых растяжении–сжатии и кручении основная нагрузка, приходящаяся на винты, фиксирующие пластину, — это сдвиговая нагрузка (срез) от пластины, вызывающая касательные напряжения. Однако вследствие имеющейся кривизны кость также испытывает изгиб от продольной нагрузки, поэтому к срезу добавляется передающаяся от подкрепляющей жесткой пластины нормальная нагрузка на винт, стремящаяся вырвать винты из кости при существенной разнице изгибных жесткостей кости (особенно поврежденного участка) и пластины. В случае расположения пластины на выпуклой стороне изогнутой кости такая вырывающая нагрузка возникает при сжатии, а на вогнутой — при растяжении. Причем подобная нагрузка тем больше, чем ближе расположен винт к вершине изгиба кости. По этой причине мы изучали не только тангенциальные нагрузки на винт, но и осевые в контактной паре винт – кость на границе раздела кости и винта. Нами установлено, что касательные напряжения, а, следовательно, и деформация кости, возрастают с увеличением длины винта, уменьшением его диаметра и толщины кортикальной пластины кости. Полученные данные могут быть интерпретированы следующим образом. Увеличение площади контакта пары винт – кость приводит к снижению напряжений во всех элементах системы винт – кость – пластина. Наименьшее напряжение в кости мы отмечали в модели с монокортикальным проведением короткого винта (3,5–4 мм). Меньший уровень касательных напряжений при использовании коротких винтов (крепление через один кортикальный слой) может быть обусловлен их меньшей длиной, в связи с чем винт при этом практически не изгибается и, соответственно, образуется меньший изгибающий момент при тангенциальной нагрузке. При этом следует иметь в виду, что погружение винта на 3,5–4 мм является менее надежным креплением пластины в связи с большей вероятностью вырыва винтов из материала кости при растяжении, особенно при наличии ее кривизны. В то же время бóльшую прочность и жесткость соединения обеспечит бóльшая площадь контакта пары винт – кость либо за счет увеличения толщины кортикального слоя, диаметра винтов, либо за счет увеличения их количества, длины и проведения винтов через оба кортикальных слоя. Напряжения в винте при таком проведении могут быть несколько выше за счет увеличившегося плеча приложения тангенциальной силы от пластины–накладки, несмотря на увеличение площади контракта винта с костью. Кроме того, длинный винт пересекает два кортикальных слоя кости и может испытывать изгиб при действии сдвиговой на- грузки на головку, еще более увеличивая уровень напряжения за счет изгибающего момента. При этом на практике приходится делать выбор между бóльшей травматичностью операции с меньшей вероятностью отрыва пластины вследствие вырыва винта или меньшей травматичностью с бóльшей вероятностью последующего разрушения узла подкрепления. Увеличение толщины кортикального слоя приводит к снижению напряжений во всех элементах системы винт – кость, так как увеличивается площадь контакта пары винт – кость. При меньшей толщине кортикального слоя кости уменьшается площадь контакта с винтом, что закономерно приводит к увеличению напряжений, которое оказывается более существенным, чем при изменении параметров винта. На основании данных фактов можно заключить, что при уменьшении толщины кортикального слоя, наблюдаемого чаще при остеопорозе у женщин, целесообразно увеличить количество, диаметр, длину винтов и толщину пластины, что увеличивает площадь контакта винт – кость, а в конечном итоге, — прочность и жесткость фиксации. В связи с тем, что при растяжении и сжатии кости от пластины на винт передается и нормальная осевая нагрузка, стремящаяся вырвать винт, также целесообразно его бикортикальное проведение, особенно при большой кривизне кости и близком расположении винта или дефекта к вершине ее изгиба. Целесообразность изучения и касательных, и нормальных напряжений, действующих на винт при выявлении механизмов его нестабильности, находит подтверждение в литературе [44, 45]. Полученные нами результаты совпадают с литературными данными, согласно которым на винт, фиксирующий пластину, действуют как радиальные, так и осевые напряжения [18, 44, 45]. При этом срезывающие напряжения играют ведущую роль в ослаблении винта, так как объем резорбции кости в перифокальной области оказался больше при радиальной нагрузке, чем осевой при всех видах нагружения [18]. По этой причине основным показателем риска ослабления винта может быть сопротивление его срезывающей силе, а не прочность на выдергивание (вырывание) в осевом направлении. Кроме того, по мнению исследователей, сопротивление радиальной силе винта в большей степени отражает физиологические кранио-каудальные нагрузки, а прочность винта на осевую нагрузку в основном определяет способность кости противостоять скручиванию [18, 44]. Бóльшие значения касательных и нормальных напряжений для перифокальной костной ткани в области введения центральных винтов говорят о потенциальной возможности первоочередной резорбции, повреждения кости и, в конечном итоге, ослабления или перелома подобных винтов. Согласно имеющимся в литературе данным, резорбция кости вызывается механическим напряжением, превышающим предел ее прочности. По мнению других авторов, критический порог для резорбции костной ткани составляет примерно 50 МПа, что ниже предела прочности кортикального слоя здоровой лучевой кости при кручении [18]. Данные получены на КЭ модели диафиза большеберцовой кости с фиксирующей пластиной и путем анализа рентгенограмм длинных трубчатых костей после выполнения накостного остеосинтеза [18]. По нашим данным, при введении винтов в кость можно наблюдать резорбцию или разрушение костной ткани в перифокальной области в случае превышении продольной (осевой) нагрузки на него, равной 100 Н, при которой почти достигается уровень допускаемого напряжения (60 Мпа), а также уменьшение толщины кортикального слоя кости. Необходимо увеличить стабильность фиксации двух центральных винтов, испытывающих наибольшие касательные напряжения, за счет увеличения их диаметра и длины для бикортикального проведения, особенно при большой кривизне кости и уменьшении толщины кортикального слоя. При этом на практике надо проявить максимум осторожности на этапе введения винтов без превышения допускаемой осевой нагрузки, избегая нежелательного повреждения кортикального слоя.

Таким образом, изучение НДС модели диафиза лучевой кости позволяет понять механизмы снижения прочности, получить представления об остаточной прочности кости после формирования краевых вырезов прямоугольной и треугольной формы, а также применения различных способов компенсации дефекта и профилактики патологического перелома. Полученные результаты с определенной долей условности можно экстраполировать в клинику для разработки способов профилактики и лечения пациентов с переломами остеотомированной лучевой кости, так как они дают представление о прочностных свойствах кости и механизмах достижения стабильности винтов при фиксации ее пластиной. Мы полагаем, что внутренняя фиксация лучевой кости пластиной на винтах может предотвратить большинство переломов, в результате чего будет достижимо уменьшение морбидности до приемлемых уровней, что позволит расширить показания к применению кожно-костного лучевого лоскута во многих областях хирургии.

ЗАКЛЮЧЕНИЕ

Наличие выреза и кривизны кости в двух плоскостях значительно повышает уровень нормальных механических напряжений в модели кости. В модели кости с треугольным вырезом отмечен меньший уровень напряжений, чем в модели с прямоугольным вырезом. Полученные данные обосновывают необходимость укрепления диафиза лучевой кости с краевым вырезом накостной пластиной независимо от его формы, что позволит снизить величину механического напряжения кости ниже допустимого уровня. Модели кости с полутрубчатой пластиной демонстрируют преимущество над моделью с пло- ской узкой пластиной, так как обеспечивают снижение уровня напряжений в большей степени. Напряжение в кости уменьшается при увеличении толщины кортикального слоя и пластины, количества и диаметра винтов.