Изучение нечёткого моделирования с использованием Mathematica 8 при подготовке специалистов на кафедре прикладной информатики КФУ

Программа Mathematica, созданная для профессионалов, с течением времени преобразилась настолько, что теперь ее могут использовать люди самых разных профессий и возрастов.

В настоящее время 100% компаний из списка Fortune 50 используют систему Mathematica для сохранения своего конкурентного преимущества в области инноваций. Половина зарегистрированных пользователей Mathematica - это коммерческие и правительственные организации, другая половина - академические заведения. Система Mathematica сегодня используется в каждом из пятнадцати основных министерств правительства США [1].

Отметим области применения системы Mathematica в мире инноваций [1]:

» Инженерное дело

• •    аэрокосмическая и оборонная промышленность;

• •    химическая технология;

• •    cистемы управления;

• •    электротехника;

• •    обработка изображений;

• •    производственная инженерия;

• •    материаловедение;

• •    машиностроение;

• •    исследование операций;

• •    оптика;

• •    нефтедобывающая промышленность;

» Финансы, статистика и бизнес-анализ

• •    актуарное дело;

• •    интеллектуальный анализ данных;

• •    эконометрика;

• •    экономика;

• •    финансовый инжиниринг и финансовая математика;

• •    управление финансовыми рисками;

» Биотехнология и медицина

• •    биоинформатика;

• •    медицинская визуализация;

• •    разработка программного обеспечения, приложений и доставка контента;

» Издательское дело;

• •    разработка интерфейсов;

• •    разработка программного обеспечения;

• •    веб-разработка;

» Наука

• •    математика;

• •    физика;

• •    астрономия;

• •    биологические науки;

• •    химия;

• •    биология;

• •    социология.

• •    статистика;

Образование и наука с Mathematica:

• -    Учебные учреждения всего мира используют Mathematica в университетском образовании.

• -    Академические издательства используют технологии Mathematica для создания сетевых версий традиционных учебников.

• -    Все 50 важнейших университетов США, предоставляющих степень доктора физико-математических наук, используют Mathematica [1].

В настоящее время в России системы компьютерной алгебры в целом широко используются в научных исследованиях в основном математиками и физиками. В промышленности, медицине, экономике, управлении и издательском деле системы компьютерной алгебры (за исключением MATLAB) в России не приобрели массового использования, как это происходит в США, Европе, Японии.

Отметим, что вступление России в ВТО приведёт к повышению конкуренции производителей. Российские предприятия будут вынуждены работать по-новому. Необходимость соблюдения международных стандартов для повышения конкурентоспособности компаний, в свою очередь, приведет к потребности в соответствующих высококвалифицированных кадрах. На рынке труда все большим спросом будут пользоваться специалисты с междисциплинарным инженерным и специальным образованием [2].

В связи с вышеизложенным в настоящее время для обеспечения:

• •    конкурентной способности наших предприятий;

• •    гибкости в управлении деятельностью предприятий;

• •    возможности эффективного принятия управленческих решений органами управления

перед учебными заведениями стоит задача по подготовке программистов нового поколения, умеющих (наравне со знанием С#, C++, 1C и т.д.):

• •    использовать системы компьютерной алгебры (Mathematica, MATLAB, Maple, MathCAD, Maxima, Sage) для составления различных приложений, решающих задачи управления;

• •    использовать системы компьютерной алгебры (равно как и другие технологии) для создания интерактивных курсов и приложений для обучения студентов и школьников. В этом направлении в уже ведется работа [3-11].

В России известные разработанные системы автоматизации в большинстве случаев непозволительно дорогие. Их могут приобретать только, как правило, большие предприятия. Однако, чтобы быть успешным не обязательно уже обладать большим капиталом. Российский бизнес уже понял это [12] и преимущества использования указанных выше специалистов (например, см. вакансии [13-15]). Заметим, что системы компьютерной алгебры (например, Mathematica, MATLAB, Maple, MathCAD, Maxima, Sage) дают отличные возможности создавать приложения для управления, в том числе и в нечётких условиях, и это, как видно [12-15], уже замечено и Российским бизнесом. В связи с этим здесь стоит отметить Российскую компанию «Практик-Групп» (Москва), основной целью которой является автоматизация бизнес-процессов компаний малого и среднего бизнеса, организовавшую в апреле 2011 года Российское турне системы Mathematica 8 [16].

К тому же, технология, работающая в нечетких условиях, завоевывает все больше сторонников среди потребителей различных систем управления. Системы, поддерживающие принятие решения в нечётких условиях разработаны и успешно внедрены [17] в таких областях, как: медицинская диагностика, техническая диагностика, финансовый менеджмент, управление персоналом, биржевое прогнозирование, распознавание образов, разведка ископаемых, выявление мошенничества, управление компьютерными сетями, управление технологическими процессами, управление транспортом, поиск информации в Интернете, радиосвязь и телевидение . Особенно важными становятся вопросы, связанные с моделированием систем «человек - машина», где остро ставятся задачи эффективного управления системами организационно-технического, экономического и социального характера.

Сегодня уже ни у кого не возникает сомнений в необходимости и нужности применения технологий искусственного интеллекта на практике. Существует множество аппаратных (нейроплаты, нечеткие контроллеры, роботы и т.д.) и программных реализаций, применяемых в различных предметных областях [18].

Многие фирмы преподносят успехи в использовании нечеткой логики как особое конкурентное преимущество. Без нее немыслимы современные ситуационные центры руководителей западных стран, где принимаются ключевые политические решения и моделируются всевозможные кризисные ситуации. Стремительное развитие теоретического аппарата нечеткого управления и средств моделирования, расширение сфер применения, коммерческий успех и широкое распространение нечетких систем со временем, возможно, вытеснят некоторые решения, основанные на традиционных методах, но более сложные в реализации [19].

Следует так же учесть, что в готовых программных продуктах, предназначенных для анализа нечётких данных, представлен не полный пакет инструментов для анализа таких данных [20]. Каждый из них разработан для определенной группы задач и в соответствии с уровнем развития самой теории нечёткого управления на момент создания программного продукта. Поэтому аналитик, пользующийся такими заготовками, изначально ограничен в свободе действий по применению новейших методов нечеткого анализа. Прежде чем использовать такой продукт надо выяснить является ли он наилучшим для решения именно Вашей задачи. Поэтому важной является задача обучения студентов самой теории нечетких множеств и нечеткого управления и разработке систем оповещения и управления в нечетких условиях.

Информационные системы, работающие с нечеткой информацией можно создавать в различных программах, например в Delphi [21],С, С++, Pascal и др., но, как правило, с гораздо большими затратами времени и сил, чем при создании их в системах компьютерной алгебы (Mathematica, MATLAB, Maple, Mathcad, Maxima). Сравнительный анализ систем компьютерной алгебры можно найти в различных обзорных статьях, например см. [22, 23]. О преимуществах программы Mathematica для создания различных информационных и управляющих систем можно познакомиться в обзорах [23-24].

В Казанском федеральном    университете на кафедре прикладной информатики в виде спецкурса для специальности 080801.65 «Прикладная информатика» читается дисциплина «Моделирование и разработка нечётких автоматов» в комплексе с дисциплинами: «Системы компьютерной алгебры в управлении» и «Теория принятия решений в нечётких условиях» после дисциплин «Теория нечетких множеств» и «Элементы абстрактной и компьютерной алгебры». В рамках этой дисциплины студенты учатся создавать автоматы для решения задач управления, анализа данных и создания информационных систем на основе нечёткой логики.

В настоящей статье рассматривается конкретная задача из области создания информационных систем. Яхъевой Г.Э. [10] рассматривалась задача о работе реактора:  требуется определить хотя бы приблизительно показание сломанного датчика давления, если показатели датчиков температуры и расхода топлива известны. Эта задача была ею решена без использования программных продуктов в частном случае при конкретных значениях температуры и расхода топлива.

Нами осуществлено моделирование работы системы оповещения о текущих показателях датчиков и с помощью пакета Mathematica 8 разработано приложение, в котором, используя теорию приближенных рассуждений для нечётких множеств, определяется приближенное значение сломанного датчика, если показания двух других датчиков известны.

В созданном приложении осуществляется выполнение оповещения об исправности датчиков, вывода их значений в случае исправности всех датчиков или подсчета и вывода приближенного значения сломанного датчика и степени уверенности в этом значении. Также выводится этап аккумуляции, из которого специалист может видеть сколько можно быть уверенным в том, что показание сломанного датчика другое.

Рекомендации по включению дисциплины «Моделирование и разработка нечётких автоматов» в рабочие учебные планы нового поколения

Дисциплина «Моделирование и разработка нечетких автоматов» читается для специальности 080801.65 «Прикладная информатика» в Казанском федеральном университете в виде спецкурса в комплексе с дисциплинами: «Системы компьютерной алгебры в управлении» и «Теория принятия решений в нечетких условиях» после дисциплин «Теория нечетких множеств» и «Элементы абстрактной и компьютерной алгебры».

Эту дисциплину, на наш взгляд, необходимо также читать по направлению

230700 «Прикладная информатика» (бакалавры, магистры), внесенному Министерством образования и науки РФ в Перечень направлений и специальностей подготовки специалистов, для которых разработаны Федеральные государственные образовательные стандарты высшего профессионального образования (ФГОС ВПО) нового поколения [25].

Преподавание этой дисциплины можно встроить в уже предложенную соответствующим стандартом схему. Почему (для обеспечения компетенций, указанных в соответствующих файлах стандарта) и как именно (за счёт каких часов) предлагается встроить - указано в таблице 1 (последние три столбца). Первые же четыре столбца этой таблицы - первые четыре столбца таблицы из указанн ых Федеральных стандартов [25].

В первой колонке таблицы 1 записан код специальности согласно указанному выше Перечню, во второй - сама специальность, в третьей - квалификация, в четвертом - дата начала действия соответствующего стандарта.

В 5-м столбце таблицы приведены учебные разделы, циклы и части, в рамках которых рекомендуется читать эту дисциплину. В предпоследнем - компетенции, которые обеспечиваются этой дисциплиной, и преподавание которой поэтому рекомендуется нами, в последнем - виды профессиональной деятельности, указанные в соответствующем стандарте нового поколения.

В таблице приведены также формулировки профессиональных компетенций (ПК) в соответствии с ФГОС ВПО нового поколения [25].

Таблица 1. Обоснование преподавания дисциплины «Моделирование и разработка нечетких автоматов» для специальности «Прикладная информатика»

Код спе циаль ности Название специаль ности Квали фикация Дата начала действия стандарта Учебные разделы, циклы и части Компе тенци и Для видов профессиональной деятельности 230700 Прикладная информатика бакалавр 22.12.2009 - Б3. Профессиональный цикл. • Базовая (общепрофессиональная) часть Как раздел дисциплины «Программная инженерия», уже внесённой в стандарт. ПК10 ПК11 ПК17 ПК19 -проектная; -организационно-управленческая; -производственнотехнологическая -аналитическая -научно-исследовательская - Б3. Профессиональный цикл. • Вариативная часть ПК10 -проектная ПК11 -организационно-управленческая; -производственнотехнологическая; ПК17 ПК19 -аналитическая где (http профес ► ПК10 – алгори ► ПК11 – ► ПК17 – алгори ► ПК19 – прикла // сиональные: способен применять к р тмов, программировать способен принимать уч способен применять ме тмическом уровнях; способен анализироват дных задач и создания и /d_09/prm78 ешению при тестировать астие в созда тоды анализ ь рынок прог нформацион кладных задач базовые алгоритмы обработки информации, выполнять оценку сложности программы; нии и управлении ИС на всех этапах жизненного цикла; прикладной области на концептуальном, логическом , математическом и раммно-технических средств, информационных продуктов и услуг для решения ных систем; Прикладная информатика магистр 21.12.2009 - М2. Профессиональный ПК7 -научно-исследовательская; 230700 цикл. • Вариативная часть ПК15 -проектная; ПК16 ПК18 где профессиональные: ►    ПК7 – способен ставить и решать прикладные задачи в условиях неопределённости и определять методы и средства их эффективного решения; ►    ПК15 – способен применять современные методы и инструментальные средства прикладной информатики для автоматизации и информатизации решения прикладных задач различных классов и создания ИС; ►    ПК16 – способен проектировать архитектуру и сервисы информационных систем предприятий и организаций в прикладной области; ►    ПК18 – способен принимать эффективные проектные решения в условиях неопределённости и риска.

Пример разработки нечёткого автомата в Mathematica 8

Задача о работе реактора. Моделирование принятия решения с помощью нечёткого логического вывода. Работа реактора описывается тремя параметрами: температура t , давление d и расход рабочего вещества r . Все показатели измеримы, множества возможных значений известны. Графики функций принадлежности имеют вид, приведённый на рис 1. Из опыта работы с реактором известны правила работы реактора, связывающие значения этих параметров:

• •    если температура низкая и расход топлива малый, то давление низкое;

• •    если температура средняя, то давление среднее;

• •    если температура высокая или расход большой, то давление высокое.

Сломался один из датчиков. Необходимо знать его показания хотя бы приблизительно, если показатели других датчиков известны.

Средняя

Температура Высокая

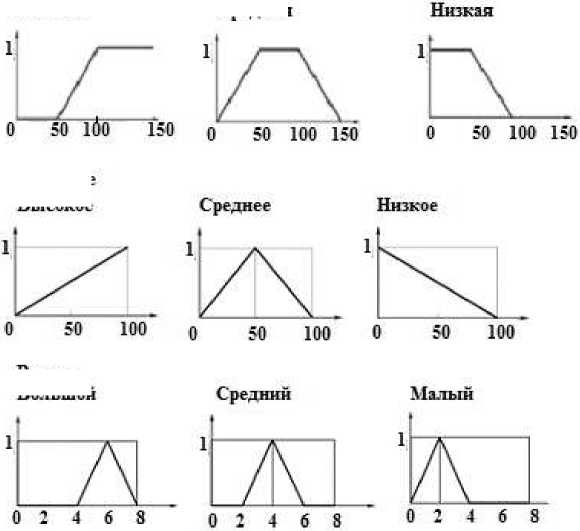
Рис. 1. Графики функций принадлежности. Решение. Введем обозначения:

Давление

Высокое

Расход Большой

T - температура низкая,

T - температура средняя,

T - температура высокая,

Д - давление низкое, Д - давление среднее, Д - давление высокое,

Р - расход малый, Р - расход средний,

Р - расход большой

Запишем соответственно правила работы реактора в этих обозначениях:

• p1:    T н ∧ P м → Д н ;

• p2:    T с → Д с ;

• p3:    T в ∨ P б → Д в .

Правила работы реактора можно записать, используя один из способов построения нечёткой импликации [11]. Будем использовать определение нечёткой импликации как минимума левой и правой частей импликации (определение

Mamdani). Поэтому функции принадлежности для этих правил соответственно будут иметь вид:

mp1(t, d, r) = mT лPm ^Д (t, d, r) = min (mT лP (t, d, r), m Д  (t, d, r)), mp2(t, d, r) = mT д (t, d, r) = min(mT (t, d, r), тд (t, d, r)), mp3(t, d, r) = m^ vp6 ^; (t, d, r) = min(m^ vp6 (t, d, r), m^ (t, d, r)), причем согласно формулам нечеткой логики для конъюнкции и дизъюнкции имеем: mT . p (t, d, r) = min (mT (t, d, r), mp (t, d, r)), TH л PM                             ' TH                   PM mT vp (t, d, r) = max(mr (t, d, r), mps (t, d, r)).

Таким образом, применив каждое из правил работы реактора к входным показаниям t = tt , d = dd , r = rr датчиков температуры, давления и расхода топлива соответственно, получим степени уверенности mp1, mp2, mp3, соответствующие этому правилу для выходной нечёткой переменной.

Здесь надо отметить, что могут быть:

• -    неизвестна переменная d и известны t = tt , d = dd (соответствует случаю -сломался датчик давления);

• -    неизвестна переменная t и известны d = dd , r = rr (соответствует случаю -сломался датчик температуры);

• -    неизвестна переменная r и известны t = tt , d = dd (соответствует случаю -сломался датчик расхода топлива;

• -    известны все входные переменные (соответствует случаю – все датчики работают, т.е. t = tt , d = dd , r = rr ;

Заметим, что согласно теории приближённых рассуждений формулы (1)-(3) содержат два первых этапа нечёткого вывода:

Этап 1. Фаззификация. По заданным значениям входных параметров находятся соответственно степени уверенности mtn[t] = mT (t, d, r) , mrm[r] = mp (t, d, r), mdn[d] = m„ (t, d, r),

Tн                           Pм                             Дн mts[t] = mT (t, d, r) , mds[d] = m„ (t, d, r),  mtv[t] = mT (t, d, r),

Tв                              Дв                             Tв mrb[r] = mp (t, d, r), mdv[d] = m„ (t, d, r)

Pб                            Дв простейших утверждений: температура низкая, расход малый, давление низкое, температура средняя, давление среднее, температура высокая, расход большой, давление высокое.

Этап 2. Непосредственный нечёткий вывод. Вычисление степеней уверенности mp1, mp2, mp3 выходной нечёткой переменной, соответствующих трём правилам работы реактора.

Далее согласно теории приближённых рассуждений осуществляем 3 этап.

Этап 3. Аккумуляция. Теперь необходимо объединить результаты применения всех правил. Сначала строим на одной плоскости графики трёх полученных функций принадлежности. Эти графики будут зависеть от того, какой именно датчик сломался: давления ( далее в программе означает x==1) , температуры (x==2) или расхода топлива (x==3) .

Далее используем один из основных способов аккумуляции — построение максимума полученных функций принадлежности и задаем функцию построения графика получившейся функции принадлежности.

Полученную функцию принадлежности уже можно считать результатом. Это новый терм выходной переменной. Его функция принадлежности говорит о степени уверенности в значении выходной переменной при заданных значениях входных параметров и использовании правил, определяющих соотношение входных и выходных переменных. Именно этот график в дальнейшем выведем в форму «контрольный блок». Но обычно все-таки необходимо какое-то конкретное числовое значение. Для его получения используется этап дефаззификации, т.е. получения конкретного значения из универса по заданной на нем функции принадлежности.

Этап 4. Дефаззификация. Существует множество методов дефаззификации [10], но в нашем случае достаточно метода первого максимума. Применяя его к полученной функции принадлежности, получаем соответствующее значение выходной переменной вместе со степенью уверенности в том, что это значение именно такое.

Система оповещения о работе реактора в Mathematica 8. С помощью системы Mathematica 8 создано приложение-автомат, сообщающий о том, какой датчик сломан и определяющий приближенное значение сломанного датчика, если показания двух других датчиков известны. Выводится также результат этапа аккумуляции. Создание этой системы осуществлено методом, изложенным выше (см. решение).

Работа созданного автомата проиллюстрирована на рис. 2-6. Ситуация на входе помещена в один файл (input.nb), а ситуация на выходе, предназначенная для диспетчера, экспортирована в другой файл (output.nb), чтобы диспетчер не видел программу, а видел только форму с результатом работы системы оповещения.

Кнопка "ситуация:" играет роль автомата, который по поступившим входным параметрам определяет выходные параметры и печатает их в "контрольный блок".

В форму «контрольный блок» записываем показания работающих на данный момент датчиков и соответствующие найденные значения сломанного датчика.

Реально сейчас мы ничего не подключаем. Поэтому кнопку «ситуация» и панель «на приемное устройство поступают значения» мы поместили на входную форму (файл input.nb) только для того, чтобы иметь возможность протестировать созданную систему оповещения. Эта кнопка и панель «на приемное устройство поступают значения» играют роль подключения.

Когда на вход не поступило никакого сигнала, т.е., подключение системы оповещения ещё не произошло, у диспетчера форма – пустое окно.

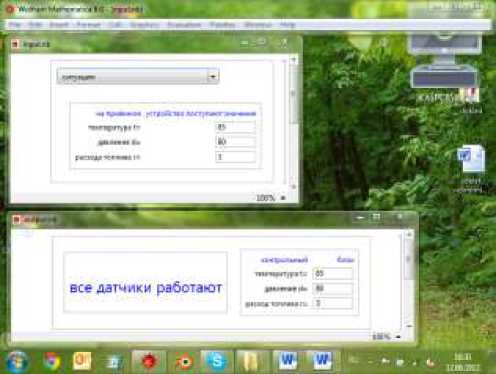
Рис. 2. Работа системы оповещения работы реактора. Все датчики работают (вход – верхняя панель, выход – нижняя панель).

Если вдруг возникает ситуация, когда сломался датчик, измеряющий давление (рис. 3), то система оповещения отсылает диспетчеру:

• -    сигнал, записанный красными буквами, с одновременным звуковым сигналом;

• -    в окне «контрольный блок» через 1 или 2 секунды отображаются:

• •    поступившие с приёмного устройства значения температуры и расхода топлива;

• •    выводится график функции принадлежности для давления в реакторе, из которого видны степени уверенности в том, что значения давления равны фиксированному значению из интервала от 0 до 100;

• •    приближенное значение давления, вычисленное по принципу первого максимума.

• •    перед вычисленным приближённым значением давления сообщается степень уверенности в том, что давление в реакторе именно такое.

Из приведённой ниже формы (см. рис. 3) видно, что в рассматриваемом случае на вход поступили сигналы: температура равна 85, расход топлива равен 3. На выходе диспетчеру сигнализируется о сломанном датчике давления и сообщается приближенное значение давления d → 49.99999978702522. , в котором мы можем быть уверенными на 99.99999957405044%, т.к. перед значением давления нам сообщается, что степень уверенности равна 0.9999999957405044. Выводится также результат этапа аккумуляции. Из этого графика (по горизонтали – значение сломанного датчика, по вертикали – соответствующая степень уверенности в этом значении) легко видеть на сколько можно быть уверенными, что показание сломанного датчика другое.

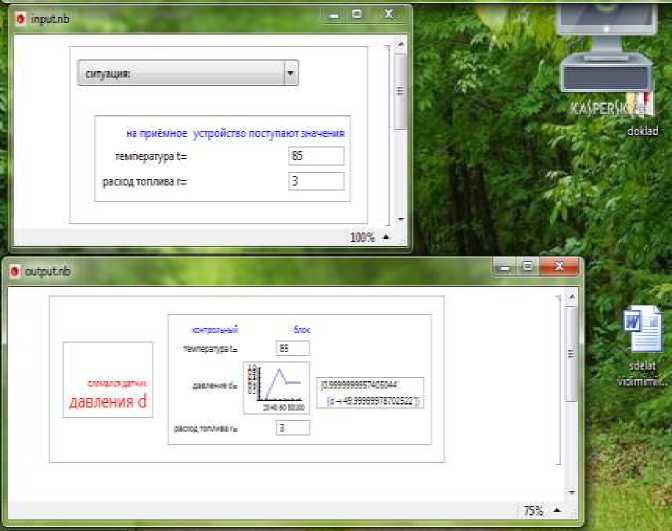
Рис. 3. Работа системы оповещения работы реактора. Датчик давления сломался (вход – верхняя панель, выход – нижняя панель).

На рис. 4 видим: если значения температуры и расхода топлива изменились, то приближенное значение давления стало соответственно другим, также как и степень уверенности.

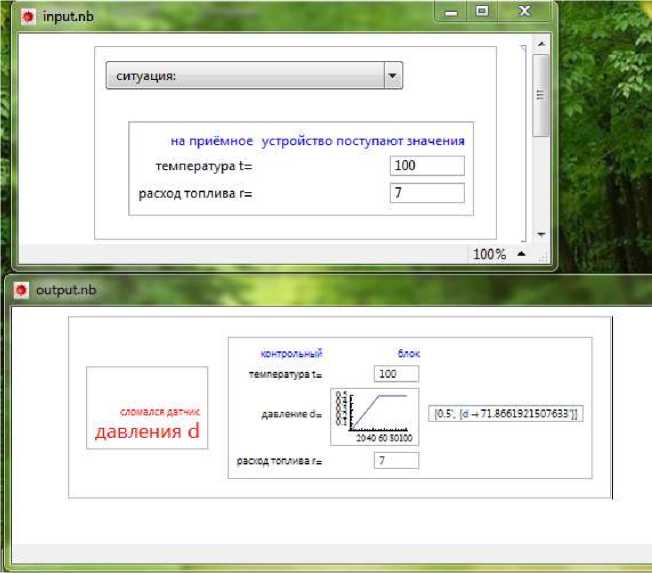
Рис. 4. Работа системы оповещения работы реактора. Датчик давления сломался. Значения температуры и расхода топлива изменились (вход – верхняя панель, выход – нижняя панель).

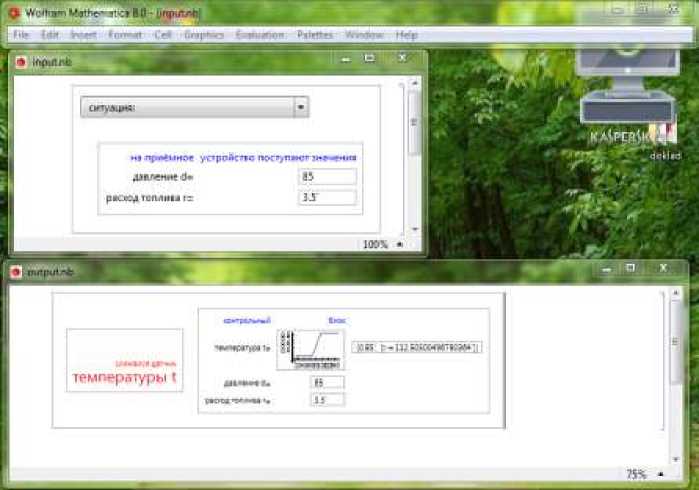
Рис. 5. Работа системы оповещения работы реактора. Сломался датчик температуры (вход – верхняя панель, выход – нижняя панель).

Аналогично в случае, если сломался другой датчик, диспетчеру выводятся соответствующие сообщения (см. рис. 5-6).

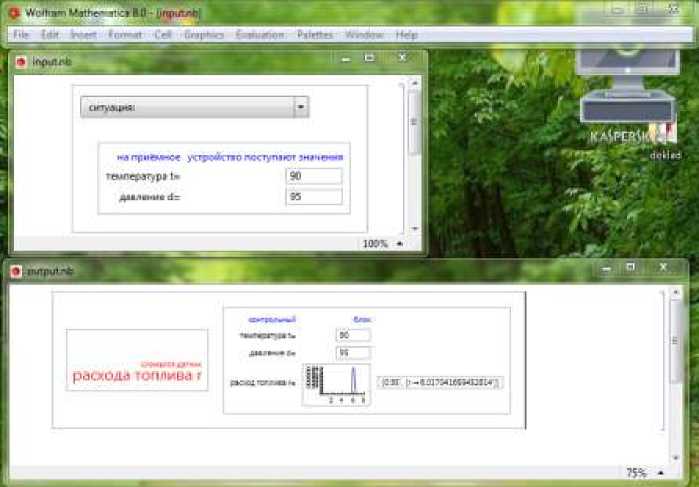
Рис. 6. Работа системы оповещения работы реактора. Датчик расхода топлива сломался (вход – верхняя панель, выход – нижняя панель).

Заметим, что выполнение оповещения об исправности датчиков, вывода их значений в случае исправности всех датчиков или подсчета и вывода приближенного значения сломанного датчика и степени уверенности в этом значении занимает не более 2 секунд на ноутбуке с оперативной памятью 1ГБ с двухъядерным процессором.

Заключение

Преподавание дисциплины «Моделирование и разработка нечетких автоматов» в комплексе с преподаванием дисциплин «Системы компьютерной алгебры (по областям)» и «Теория принятия решений в нечетких условиях» для направления 230700 «Прикладная информатика» может способствовать формированию упомянутых в статье профессиональных компетенций.

Приведенный пример реализации в Mathematica 8 системы оповещения о текущих показателях датчиков может быть использован в учебном процессе в качестве примера моделирования автомата.