Извлечение надежного сигнала из гетерогенных данных

Извлечение общего надежного сигнала из данных, разделенных на разнородные группы, является сложной задачей, когда каждая группа - в дополнение к сигналу -содержит большие уникальные вариационные компоненты. Ранее максиминая оценка была предложена в качестве надежного метода при наличии неоднородного шума [1-3]. Предлагается мягкая максиминная оценка максимального значения в качестве привлекательной с вычислительной точки зрения альтернативы, направленной на достижение баланса между объединенной оценкой и (жесткой) оценкой максимального значения [4-6]. Метод мягкой максиминной оценки предоставляет диапазон оценок, управляемых параметром ξ>0, который интерполирует объединенную оценку наименьших квадратов и максиминную оценку. Устанавливая соответствующие теоретические свойства, утверждается, что метод мягкой максиминной оценки является статистически обоснованным и привлекательным с точки зрения вычислений. Демонстрируется на реальных и смоделированных данных, что мягкая максиминная оценка может предложить улучшения как по сравнению с объединенными OLS, так и по сравнению с жестким максимином с точки зрения производительности прогнозирования и вычислительной сложности. Эффективная по времени и памяти реализация предусмотрена в пакете R SMME, доступном на CRAN [4].

Рассматривается проблема извлечения общего сигнала из разнородных данных [7]. Поскольку гетерогенность преобладает в крупномасштабных системах, цель – эффективный в вычислительном отношении оценщик (решение) с хорошими статистическими свойствами при различной степени неоднородности данных.

МАТЕРИАЛЫ И МЕТОДЫ

Чтобы конкретизировать концепцию неоднородности, рассмотрим линейную модель смеси с одномерными переменными отклика Y 1 ,..., Y n , сгенерированными как

Y i = X i^⊤ B i +ε i , i = 1 , … , n . (1)

Здесь ε 1 , … , ε n и векторы признаков X 1 , … , X n являются p-мерными случайными величинами, а B 1 , … , B n - одномерными шумовыми переменными. Векторы признаков наблюдаются и предполагаются независимыми одинаково распределёнными случайными величинами, а шумовые переменные предполагаются независимыми одинаково распределёнными случайными величинами. Ненаблюдаемые переменные B 1 , … , B n распределены идентично распределению F B , но не обязательно независимы [1].

Неоднородность в модели, приведенной в (1), обусловлена изменением смещения, регулируемым F B . Поскольку B i может быть зависимым, модель (1) может фиксировать неоднородность, вызванную структурой группы, то есть, когда данные поступают с естественной группировкой, а Bi постоянен внутри групп, но различается между группами. Даже если данные не сгруппированы или если структура группы неизвестна, полезно изучить настройку с известной структурой группы. В приведенном в [1] примере совместного использования объектов групповая структура вводится для представления временной неоднородности и [1] демонстрирует, как создавать групповые структуры как часть вывода, когда группировка не задана.

Поэтому сосредоточимся на настройке с группами G и с постоянными B i внутри групп. Цель состоит в том, чтобы изучить один β ∈ R^p, который можно разумно рассматривать как общий сигнал B i . Объединение данных по группам и вычисление обычной оценки наименьших квадратов (OLS) может быть ненадежным, в зависимости от F B , и в [1] введена максиминная оценка в качестве надежной альтернативы OLS для разнородных данных из модели (1). Общим сигналом, оцениваемым с помощью оценки максимина, является количество населения, называемое максиминным эффектом.

Хотя максиминная оценка надежна, она также может быть консервативной, и предлагается мягкая максиминная оценка, чтобы обеспечить хороший баланс между максиминной оценкой и объединенной оценкой OLS. Баланс контролируется параметром настройки ξ>0, при этом ξ→∞ соответствует максиминной оценке. На рис. 1 показан результат применения мягкой максиминной оценки для трех значений ξ, а также объединенной оценки OLS к реальному набору данных. Это иллюстрирует, как прогностическая эффективность двух экстремальных оценок интерполируется с помощью мягкой максиминной оценки, определяемой количественно как кумулятивная среднеквадратичная ошибка (RMSE) с течением времени.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Далее представим методологию в постановке с заданной структурой группы и воздействуем на константу B i внутри каждой группы. Это, в свою очередь, подразумевает конечную поддержку F B , и эту модель, возможно, лучше понимать как тип линейной смешанной модели, поскольку группировка доступна, следовательно, больше не является частью вывода. Однако, в отличие от традиционной смешанной модели, мы избегаем явного моделирования фиксированных и случайных эффектов, поскольку цель не состоит в том, чтобы делать выводы о них. Вместо этого мы стремимся получить только оценку возможных общих эффектов, присутствующих в данных.

Чтобы ввести G ∈ N групп для модели (1), предположим, что задано разбиение I 1 ,..., I G набора индексов {1,..., n} такое, что |Ig|=n g , а n=∑ g n g , где для каждого g и для всех i ∈ Ig, B i =Bg выполнено в группе g. Таким образом, F B имеет конечную неизвестную поддержку с мощностью G, то есть supp(F B ) = {b 1 ,..., b G } ⊂ Rp с b g ∶ =B g (ω) - неизвестным эффектом в группе g.

Используя эту дополнительную структуру, мы можем пометить откик, ковариаты и ошибки в соответствии с группой.

Для g-й группы пусть Y g =(Y g,1 ,..., Y g,ng ) ⊤ - вектор отклика n g ×1, X g =(X g,1 ,..., X g,ng ) ⊤ матрица проектирования n g ×p и ε g =( ε g,1 ,..., ε g,ng ) ⊤ - вектор ошибки n g ×1. Линейная модель для g-й группы тогда представлена как

Y g = X g b g + ε g , g ∈ {1 , … , G} .                             (2)

Общий сигнал в этой структуре представлен как β ∈ R p таким образом, что X g является хорошей и надежной аппроксимацией X g b g во всех группах G.

Чтобы оценить качество аппроксимации, используем критерий оптимальности [1]. Там объясненная дисперсия в группе g при использовании некоторого β ∈ R p в (2) определяется как

V bg ( e ):= 2 в ^т 2Ь д - в ^т £ в .                              (3)

Таким образом, оптимальным приближением для всех групп является так называемый эффект максимина, определяемый как b ^∗ ∈ R^p, который максимизирует минимум объясненных различий между группами, то есть, b * :=arg max p min g V bg ( в ).

Поскольку b g неизвестен, то, чтобы сделать этот критерий работоспособным, обозначим через ^_д = X_gX_g/n_g эмпирическую матрицу Грама в группе g. Заменив Е на Σ g в (3), мы получим эмпирически объясненную дисперсию в группе g:

V g ( e ):=(2 e ^T Eb g - в ^т Е в )/п д .

^Ф): = i (2/? ^ X j Y_g - Г X. X . .J,)                    (4)

llg

Как показано в [1], использование этой оценки может привести к более надежным оценкам для разнородных данных по сравнению с оценкой, которая не учитывает группировку, то есть объединенной оценкой. Предположение заключается в том, что максимальная оценка извлекает только те объекты, которые активны с одинаковым знаком в разных группах, при этом для объектов, специфичных для группы, устанавливается нулевое значение. Это делает ее более грубой оценкой по сравнению с оценкой, полученной с использованием методологии полной смешанной модели; однако в принципе она также более надежна и потенциально более привлекательна с точки зрения вычислений. В крупномасштабных системах обработки данных, где обычно встречается неоднородность данных, вычислительный аспект оценки имеет решающее значение.

Устраним это вычислительное препятствие, заменяя функцию максимума следующей гладкой функцией. Для G∈N и ζ≠0 рассмотрим масштабированную экспоненциальную функцию lse логарифмической суммы logCEje^A         r lse^(x) = —----, x £ Rg                         (5)

Очевидно, что lse дифференцируема, она обладает дополнительными свойствами, которые делают ее хорошо подходящим для целей оптимизации. Основные свойства, изложенные далее, легко проверяются и объясняют, почему (5) является разумным выбором в качестве аппроксимации функции максимума.

Предположение 1. Пусть GeN и x£R G .

• (1.1)    При ζ >0

  Современные инновации, системы и технологии // (cc) ® 2024; 4(1) Modern Innovations, Systems and Technologies

max(x1,...,xG) < lse^(x) < ZO0(G^ + max(x1,...,xG)             (6)

и, в частности, lse(x)Xmax g {x g } при Z ^ ”.

• (1.2)    При ζ → 0

  G lse ^ (x) ⁼ q^x j +

  
  

  log(G) S

  
  

  + o(1)

  
  

Определим мягкую функцию максимальных потерь как

s^P) = lse^(—V(P)), PeRM>0

где V(P) = (Vi(P),... ,VG(P))T. For k > 0 и Z > 0, оценка мягкого максимума теперь может быть определена как

Psmm = argminp lse^(—V(p))  такое, что IIPII1 < k              (7)

Используя Предположение 1, можно количественно оценить влияние параметра на производительность оценки мягкого максимума (7). Следующий результат дает оценку максимальной отрицательной объясненной дисперсии оценки мягкого максимина, используя оценку теоретического эффекта максимина b ^∗ .

Утверждение 1. Пусть D = maxg\\2g — 1\\^и 5 = max^^Xjf^y . Для фиксированных ζ>0 и k>0, при k≥maxg ||bg||1, выполнено log(G) ^

maxg {—V6fl(/?skmm)} < maxg j-V^b*)} + 6Dk2 + 4k5 + где b∗ - максимальный эффект. В частности y/?^m — 6’L < 6Dk2 + 4k5 + l2g(^)

²                           s

Утверждение 1 доказывается путем объединения Предположения 1 и результатов [1]. В частности, потеря производительности, возникающая при использовании оценки мягкого максимума, ограничена той же величиной, что и у максиминной оценки, плюс логарифм смещения аппроксимации мягкого максимума log(G)/ζ из Предположения 1. Таким образом, при управлении параметром ζ мягкая оценка максимина обладает теоретическими свойствами, аналогичными свойствам (жесткой) оценки максимина. В частности, для D=0 (например, для фиксированного проекта) и фиксированного числа групп, если ng→∞ для всех g, оценка мягкого максимина сохраняет только смещение аппроксимации.

Утверждение 1 устанавливает связь между производительностью мягкого максимина и эффектом максимина и показывает, что для ζ ↑∞ мы действительно получаем максиминную оценку производительности. Однако это также подчеркивает, что при ζ ↓0 производительность мягкой оценки максимина может сколь угодно сильно отклоняться от производительности оценки максимина. Действительно, согласно Предположению 1, для малых ζ >0,

G ^П ^

■'!■■■ 'XI . ^ '

l=i j=i l=i J и (7) фактически становится задачей взвешенных наименьших квадратов со штрафом (PWLS) по всем n наблюдениям. Таким образом, решение (7) для малого ζ=0 приблизительно дает объединенную оценку PWLS с весами, усиливающими наблюдения из групп меньшего размера, чем в среднем. При одинаковом количестве наблюдений в каждой группе программа оценки мягкого максимума, в свою очередь, интерполирует объединенную оценку PLS и максимальную оценку.

В этом смысле ζ отражает неоднородность данных. При небольшой неоднородности может хорошо работать низкий или даже нулевой показатель, соответствующий тому, что группировка не является релевантной. Однако для разнородных данных малое значение может привести к прогнозам, которые будут хуже нулевого прогноза, в то время как большое значение все еще может работать хорошо.

Чтобы проиллюстрировать интерполяцию, рассмотрим небольшой пример данных, сгенерированных в соответствии с (2) с G=20 группами, n g =400 наблюдений в каждой группе и двумерным (2D) пространством параметров. Для фиксированных эффектов {b i ,..., b 2o } C R² мы производим выборку X g и g, M=10 раз для каждого g, в результате чего получаем 10 различных наборов данных. Для каждого из этих десяти небольших наборов данных мы можем вычислить мягкую максиминную оценку (т.е. k=∞ в (7)) для последовательности значений ζ .

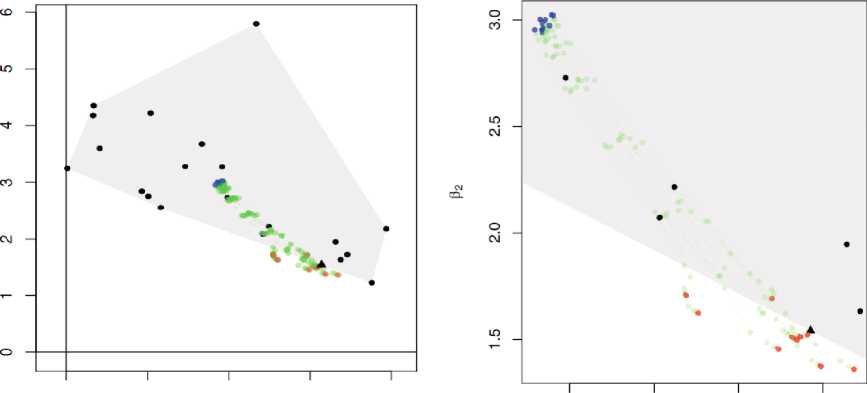
На рис. 1 показаны пути интерполяции мягкой максиминной оценки, соединяющие оценки LS населения и оценки maximin. Обратите внимание, что все оценки типа maximin сгруппированы вокруг теоретического максиминного эффекта, обозначенного символом ^А на краю выпуклой оболочки {b i ,..., b 2o }, в то время как объединенные оценки находятся далеко внутри выпуклой оболочки.

Важно, что другой метод регрессии, якорная регрессия, был предложен в [6] для обработки неоднородности данных в ситуациях, когда распределение ответов может смещаться, что приводит к разнице между распределением обучающих данных и распределением тестовых данных. Если эта неоднородность может быть закодирована или сгенерирована известной опорной переменной, их метод может привести к улучшенной и, в частности, более стабильной производительности прогнозирования. В частности, контролируя параметр привязки γ >0, этот метод интерполирует три различных метода регрессии, где γ =1 дает регрессию OLS, а γ =∞ - регрессию инструментальной переменной.

0.0        0.5        1.0        1.5        2.0

1.0         1.2          1.4          1.6

Pi ₽1

а)                                                     б)

Рисунок 1. (a): выпуклая оболочка (серая заштрихованная область) supp (F B ) (черные точки). Теоретический максимальный эффект b ^* =, максимальные оценки (красные точки), мягкие максимальные оценки (зеленые точки) для различных ζ и популяционные оценки OLS (синие точки). (б): крупный план.

Figure 1. (a): convex hull (gray shaded area) supp (FB) (black dots). Theoretical maximum effect b*=, maximum estimates (red dots), soft maximum estimates (green dots) for various ζ and population OLS estimates (blue dots). (b): close-up.

В некотором смысле точка привязки играет роль группирующей структуры I 1 ,..., I G , используемой в определении оценки мягкого максимума. Однако в общей настройке с неизвестными группами, учитывая определенные структурные допущения, можно построить наборы индексов I 1 ,..., I G , как в примере выше, или путем случайной выборки.

Теоретические гарантии в этом случае даны в [1] для максимальной оценки и аналогично Утверждению 1 должны распространяться на оценку мягкого максимума.

В дополнение к математической сложности, это добавляет процедуре вывода существенный уровень вычислительной сложности, поскольку число групп G в таком случае является гиперпараметром, который необходимо вывести, например, путем перекрестной проверки (CV). Таким образом, этот уровень кластеризации только усиливает важность эффективно вычисляемой базовой оценки.

ЗАКЛЮЧЕНИЕ

Таким образом, оценка мягкого максимума будет практически полезна в ряде различных контекстов как способ агрегирования объясненных отклонений по группам. В частности, потому, что она снижает вес групп с большой объясненной дисперсией, которые могут быть просто выбросами, что может полностью заглушить сигнал.