Ядерная магнитная релаксация и неаффинная деформация в сшитых эластомерах

Одними из наиболее информативных методов исследования крупномасштабных движений молекул и состояния сетки химических сшивок в сшитых эластомерах являются методы ядерной магнитной резонансной спектроскопии и релаксометрии. Среди них особый интерес представляют исследования в образцах, подвергнутых деформации растяжения [1-5]. Анализ результатов работ [1-3] по измерению времени поперечной релаксации и второго момента в сшитых эластомерах показал, что зависимости полученных параметров от степени растяжения оказываются слабыми и не согласуются с теоретическими [4-6], построенными на основе предположений о том, что функция распределения расстояний между химическими сшивками является гауссовой, полные контурные длины всех цепей сетки одинаковы и деформация является аффинной.

Целью данной работы является проведение нового эксперимента по снятию спада поперечной намагниченности и определению второго момента остаточного диполь-дипольного взаимодействия в зависимости от степени растяжения и объяснение полученных результатов на основе введения в рассмотрение ланжевеновской функции распределения вместо гауссовой и на учете неаффинности деформации образца.

Объекты и методы исследования

Объектами исследования служили 4 образца полиизопренового каучука СКИ-3, вулканизованного серой с концентрацией 1 мол. %. Один из них служил в качестве исходного, а 3 подвергались различной степени одноосного растяжения. Растянутые образцы готовились следующим образом. После соответствующего растяжения полоски исходной резины фиксировались зажимами и помещались внутрь полости, которая заполнялась эпоксидной смолой. После суточной выдержки и отверждения смолы из полученного бруска вырезалась центральная часть длиной ~20 мм, которой путем слесарной обработки придавалась форма цилиндра. Образующая цилиндра была параллельна оси растянутого образца, а его диаметр был несколько меньшим внутреннего диаметра пробирки спектрометра. При помещении полученной таким образом капсулы внутрь пробирки, а последней - в датчик спектрометра, ось растяжения образца оказывалась направленной поперек магнитного поля спектрометра.

Рис. 1. Капсула с образцом: 1 - оболочка из затвердевшей эпоксидной смолы, 2 - растянутый вдоль оси симметрии образец каучука

Во всех исследуемых образцах с помощью импульсной последовательности Хана на резонансной частоте протонов 25 МГц были сняты спады поперечной намагниченности (СПН). Во избежание нарушения целостности эпоксидной оболочки капсулы эксперименты проводились только

Физика

при одной температуре 21,5 °C. Для нахождения времени затухания в области высокотемпературного плато Т™ СПН исходного образца был представлен в виде

4 (О=ехр(-^-)ЛШ (о,                           (1)

где Г2б - время, описывающее быстрые мелкомасштабные (сегментальные) движения, А™^-спад поперечной намагниченности в области плато времени затухания поперечной намагниченности. После деления полученного при высоких температурах А^1^ на А (О ПРИ комнатной температуре в исходном образце было найдено время Т^. Оно оказалось равным 2,5 мс. Принимая согласно [2, 3], что Т2б при растяжении не изменяется, из полученных в эксперименте Аг (f) по уменьшению в е раз были получены значения Т™ в растянутых образцах. Для проверки правомерности такой методики расчета Т™ один из образцов со степенью растяжения Л = 2 был нагрет до 80 °C. Оказалось, что измеренное в эксперименте время Т™ (1,42 мс) практически совпадает с рассчитанным (1,45 мс). Второй момент остаточного диполь-дипольного взаимодействия рассчитывался как М^ = ——— для гауссового СПН. Верхний индекс 90° - угол а между на правлением вытяжки N и полем Но .

Результаты и обсуждение

Найденные значения Г₂^ПЛ и М^ для каждой степени растяжения приведены в табл. 1. В нашей работе проведен также анализ данных работы [3], в которой авторы осуществляли растяжение образца натурального каучука вдоль направления внешнего магнитного поля Н_о . Второй момент М^ был найден авторами из Д-эхо-функции. Верхний индекс 0° - угол а между направлением вытяжки N и полем Н_о . В табл. 2 приведены данные работы [3].

Таблица 1

Значения Т₂^ПЛ, М* и М₂,- в зависимости от растяжения к в нашем эксперименте

Я	1	2,0	3,0	4
7)™, мс	1,6	1,4	1,2	1,0
ЛД90 Х10"6, с"2	0,73	0,96	1,5	2,0
Л/2,Х1ОЛ С’2	0,73	1,15	1,86	2,45

Таблица 2

Значения M”" и М₂,-в зависимости от растяжения Я в эксперименте 3] ___________

Я	1	1,05	1,18	1,40	1,53	1,75	2,14	2,48	3,03	3,33	3,96
М^ хЮ"6, с-2	1,2	1,3	1,4	1,5	1,6	2,1	2,7	3,5	4,5	6,8	8,3
ЛДхЮЛ с 2	1,2	1,28	1,34	1,38	1,45	1,85	2,31	2,93	3,68	5,49	6,54

Значение второго момента определяется как степенью растяжения образца Я, так и углом а.

Первое связано с увеличением длин векторов 7?, соединяющих узлы сетки, второе - с ориентирующим фактором, обусловленным преимущественной ориентацией этих векторов вдоль на правления вытяжки N, происходящих при увеличении Л. Второй момент можно представить в форме [3]

М^ = 5М^

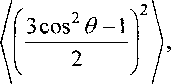
где 6 - угол между векторами R и N,<...> - среднее по распределению в, Му - изотропнопорошковый второй момент.

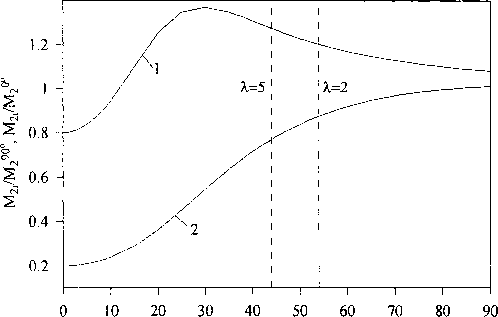
о, град

Рис. 2. Зависимости отношений М2/М2Э0(1) и М2/М2°" (2)

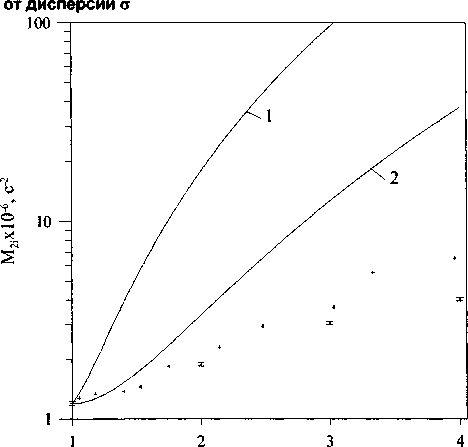
X

Рис. 3. Зависимость изотропно-порошкового второго момента M₂i от степени растяжения Л. Точки - экспериментальные значения, найденные в данной работе (•) и в [3] (+). Сплошные линии - теоретические кривые, полученные в предположении гауссовского (1) и ланжевеновского (2) распределений расстояний между узлами химических сшивок и аффинной деформации образца

На рис. 2 приведен результат расчета отношений вторых моментов Мц/М^и М-ц / М® , проведенного в предположении гауссового распределения углов 6 с варьируемой дисперсией о. В работе [3] экспериментальным путем получено, что растяжениям 2=5 и 2 = 2 соответствуют ст =44° и <7= 54°, обозначенные на рис. I вертикальными линиями. Пересечение этих линий с кривыми отношений вторых моментов дает по две реперные точки зависимостей Л/₂1/А^2° и Мц/М^ от 2. Третьей точкой этих зависимостей служила точка Мц / М^ = Му / М^ = 1 при 2=1. После проведения через эти точки плавных линий нами были найдены изотропно-порошковые вторые моменты Му для всех 2 в обоих экспериментах (табл. 1 и 2). Как видно из табл. 1 и 2, изотропно-порошковые Му слабо отличаются от М^ и Mi. Это свидетельствует о том, что ориентирующий фактор является слабым и распределение по углам 6 близко к равновероятному.

На рис. 3 приведены экспериментальные и теоретическая [7]

1 /       97 1

Му = - 24—2 +у (3)

33 2

зависимости MyQ.\ Последняя получена в предположениях гауссовского распределения расстояний между узлами химических сшивок и аффинной деформации образца. Для удобства сравнения полученных данных нами была проведена процедура масштабирования так, чтобы как экспериментальные точки, так и теоретическая кривая выходили из одной и той же точки при 2=1 эксперимента [3]. Как видно из этого рисунка, теоретическая зависимость Му^Х) (кривая 1) значительно более сильная, чем экспериментальные.

Одной из причин несоответствия между теорией и экспериментом, как мы полагаем, является использование в классической теории упрощенной модели гауссовых цепей, которая применима только тогда, когда расстояние между узлами цепи много меньше контурной длины молекулы, что имеет место только при слабых растяжениях (2 < 2). В более общем случае, как показано Куном и Грюном [10], необходимо использовать ланжевеновские цепи, для которых второй момент остаточного диполь-дипольного взаимодействия в отсутствие растяжения в соответствии с [9] должен быть записан в виде

3L(pV\

М^мУ 1--.                     (4)

В выражении (4)

Физика

где L - функция Ланжевена, р = argi — I - обратная функция Ланжевена, а М2 - второй мо мент жесткой решетки, п - число сегментов Куна в цепи сетки, / - длина сегмента.

При деформации сетки химических сшивок вектор R переходит в новый вектор R'. При условии, что имеет место сохранение объема, R и R' связаны друг с другом следующим образом

[7]:

2 _1

(ба)

а когда деформация растяжения происходит вдоль внешнего магнитного поля и

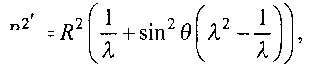
если растяжение осуществляется поперек внешнего магнитного поля. Полагая, что распределение по 6 является равновероятным, получаем средние значения (cos² 9) = (sin² 9) = 1/3 . С учетом этого после подстановки (ба) и (бб) в (4) для Мц имеем

Mlt=M^

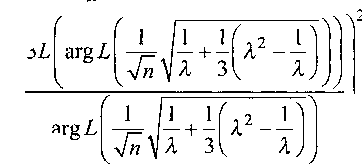
ЪЬ arg А

На рис. 3 приведена функция (7) (кривая 2). Видно, что замена упрощенной модели гауссовских цепей на ланжевеновские дает на порядок лучшее соответствие между теорией и экспериментом. Тем не менее, различие между теоретическими и экспериментальными зависимостями остается значительным.

Мы считаем, что основной причиной несогласия теории с экспериментом является распределение густоты химических сшивок по объему образца и, как следствие, неаффинность деформации образца при его растяжении. В процессе производства одни части образца сшиваются в большей степени, другие - в меньшей. Представим далее образец каучука как совокупность однородных образцов, отличающихся друг от друга степенью сшивания. Пусть плотность химических сшивок v изменяется вдоль оси растяжения образца непрерывно от v^ до . Из найденной в работе [9] связи v ~ aJm^ следует, что в качестве функции плотности распределения следует выбрать функцию р^М₂ ). Тогда после введения обозначения ^М₂ - и результирующий СПН А^ (t) при растяжении образца в А раз должен иметь вид

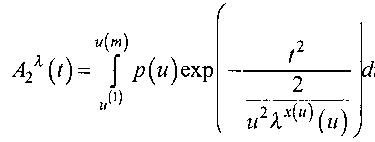
где А^ы^ (и) определяется из графика теоретической зависимости второго момента для ланжеве'

новских цепей (рис. 3, кривая 2) как отношение второго момента при растяжении А ко второму моменту без растяжения. Для каждой степени растяжения по уменьшению сигнала А^ (?) в е раз определялось время поперечной релаксации Т₂ , а затем рассчитывался второй момент M_2i.

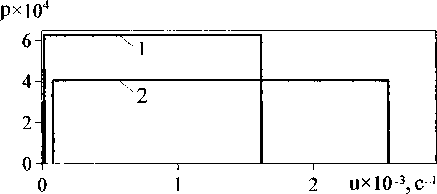
Рис. 4. Функция плотности вероятности р(и) для зависимостей Му (Л), полученных в данной работе (1) и в [3] (2)

Для нахождения закона изменения степеней растяжения Л (и) вдоль оси деформации образца, мы исходили из того, что наша система находится в равновесии - сила, прикладываемая к любому элементу образца имеет одно и то же значение. Из связи силы с механическим напряжением Н и закона сохранения объема образца получаем

du

С другой стороны, из теории упругости каучука [8] следует, что приложенное напряжение связа но со степенью растяжения соотношением

Н = G\ Я²--,

(Ю)

„ ypRT              „    , ,                                          ,       „ где G = —---, у - числовой коэффициент, величина которого зависит от особенностей структу-Мс ры сетки, R - газовая постоянная, Т - температура, Мс - молекулярная масса части молекулы, лежащей между последовательно расположенными точками поперечных сшивок, р - плотность полимера. Используя полученную в работе [9] связь между М и Мс

(И)

выражение (10) перепишется в виде

Н~и Л²(и)

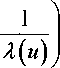
примет вид

После введения обозначения

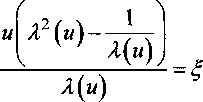
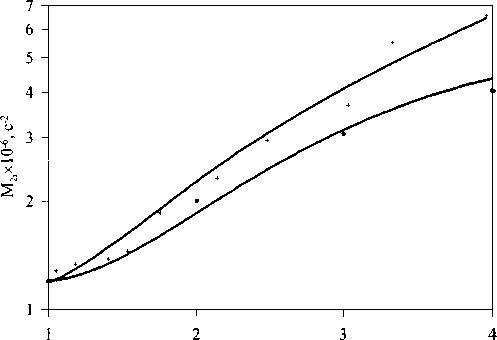
Рис. 5. Зависимость второго момента Му от степени растяжения X образца. Точки - экспериментальные значения, полученные в данной работе (•) и взятые из работы [3] (+). Сплошные линии - теоретические кривые, полученные в предположении ланжевеновского распределения расстояний между узлами химических сшивок и учета неаффинности деформации образца

система уравнений для нахождения Я (и)

[^ = 0 du

'                            .            (13)

Л = J p^uy.^u^du

При осуществлении подгонки теоретической зависимости M_2i (Я) к экспериментальной было установлено, что подбор функции р(и) - процедура неоднозначная. Необходимо учитывать форму СПН и подбирать физически реальные значения вторых моментов при растяжении. Наиболее простыми и, в то же время, удовлетворяющими этим требованиям являются прямоугольные распределения, изображенные на рис. 4. Найденные для них теоретические зависимости M_2i (Я) представлены на рис. 5.

Физика

Основной результат данной работы - факт неаффинности деформации сшитого полимерного образца находится в явном противоречии с классической теорией упругости каучуков [8, 10]. Мы полагаем, что это противоречие разрешается тем, что выявленная нами неаффинность касается только микроуровня, определяемого средним расстоянием между сшивками. Таким образом, мы констатируем, что на микроуровне деформация образца является неаффинной, а на макроуровне - аффинной.

Выводы

Использование модели ланжевеновских цепей вместо гауссовых дает на порядок лучшее соответствие между теоретическими и экспериментальными зависимостями А/ДЛ)- В то же время различие между этими зависимостями остается весьма значительным.

Основной причиной несогласия теории с экспериментом является распределение густоты химических сшивок по объему образца и, как следствие, неаффинность деформации образца при его растяжении.

Учет неаффинности деформации, осуществленный подбором распределения густоты сшивок по объему образца позволил добиться полного совпадения теоретических и экспериментальных зависимостей второго момента остаточного диполь-дипольного взаимодействия от степени растяжения.

На микроуровне деформация образца является неаффинной, а на макроуровне - аффинной.