Явная разностная схема решения одномерного квазилинейного уравнения теплопроводности

В настоящей работе используются идеи, изложенные в работах [1, 2], в которых была предложена и обоснована явная устойчивая схема для линейного уравнения теплопроводности.

I I ГА/1'Т «X Ж Ж /Д Г> 1'0 OOnOUW HUt 1 clHUoKd 5d,ld4H

Рассмотрим следующую постановку третьей смешанной задачи для одномерного однородно -го квазилинейного уравнения [3]:

с (u) It = f q (u) lu ^,         0 < t - T, 0 < x < L, d t dx V    dx )

и ( x , 0) = ^ ( x ),

= X ( и (0, t )) (9₁ - и (0, t )) + Q i , x = 0

^f q ( и )| u )    = X r ( и ( L , t )) (9 r - и ( L , t )) + Q r ,

[V     dx V x=L где и = и(x, t) - искомая функция (температура стержня), 0 - x - L, 0 -t - T; L - длина стержня; T - конечный момент времени; с(и) - заданная объемная теплоемкость материала стержня; q (и) - заданная теплопроводность материала стержня; ф(x) - заданная функция начального распределения температуры стержня; Xi (и) - коэффициент теплоотдачи на левом конце стержня; Xr (и) - коэффициент теплоотдачи на правом конце стержня; 9i - температура внешней среды на левом конце стержня; 9r - температура внешней среды на правом конце стержня; Qi - мощность потока тепла на левом конце стержня; Qr - мощность потока тепла на правом конце стержня. Функции c = с(и), q = q(и), Xi = Xi (и) и Xr = Xr (и) предполагаются непрерывными функциями температуры, заданными для всех значений температуры.

Замена искомой функции

Поскольку в уравнении присутствует член q ( и ) —, то удобно сделать следующую замену: d x

u

G ^{( и} ) = J q ( £ ) d^.

G д G      д 2 G

— = a ⁽ и )—_т,                             ⁽²⁾

о t         дx

Геренштейн А .В., Хайрисламов М.3.

где a ( u ) = qq^u)- — коэффициент температуропроводности.

\ c ( u )

Функция G ( u ) является строго монотонной функцией температуры.

Вывод рабочих формул

На плоскости ( x , t ) используется равномерная сетка [2]

^_т = ^ х < у ., ^ = x,- = f i -— | h , i = 1,2,..., N , h t h i h z            2

®T = {tj = jT, j = 0, 1,...}, где h = ^ - шаг по переменной x, т - шаг по переменной t. Шаблон предлагаемой схемы представлен на рисунке.

Пусть (l (t) = G if i -11 h, t j - значения функции G в сечении x = f i -1J h. Запишем урав- нение (2) для точки if i -^ J h, t j, заменив вторую производную по пространственной координа-

Г*Г\Г\ТП АТРТПЛ^КАТТТАР ПЯРЦАРТЦПА АААТТЦТАТТТАКГТЯА ’ ПЛ Wv ПЗС IV ИЗ у ГХ_/1_ЦСС UdOrlV/^ 1_Г1х_/С V' v v l НУ >1 I IC3M ИС7.

t t 0 + т

т

t о

.................f G z ^l '¹

G - 1     G z     G .

I +1

t 0 ^{- т}

1        2

• V к h     2 h

i

• ^x . - i     ^x .      ^x

• ¹    I ^A I. *

ih

N N + 1 x

Nh = L

Шаблон разностной схемы d^ = a 2( u,) dti

G .-i ( t ) - 2 G . ( t ) + G . +i( t )

h h

, t e [0; т ], i = 2,..., N - 1.

Аппроксимируем значения G_z , ( t ) и G_{z +1} ( t ) с точностью до членов первого порядка малости:

G i-1 ( t ) « G i-1 (0) + dG^ -^ (0) t , G +1 ( t ) « G +1 (0) + dG i+^ (0) t .

dt                             dt

В результате уравнение (3) преобразуется к виду dGi(t)2a2(u.)r. . a2(u.)

¹ G . ( t ) = dt h ²                h h-

G -1 (0) + G i+1 (0) +1 dG i^-^ (0) + d^{Gi +1} (0) 1 1 I . f dt dt 1 1

dG^-1 (0) и dt

т

Погрешность аппроксимации оказывается равной O — , даже если производные f h ² 1

¹⁺¹ (0) вычисляются по формулам первого порядка точности.

dt

Решением уравнения (4) является функция

- ^{2 a 2}( u i ) _t

Gz(t) = (Gz(0)-B)e h2   + At + B, te [0; т], где A =11 dG^-1 (0) + dG^i1 (0) |, B =

2 f dt dt J

G -1(0) + G +1(0) --A .

h 2

2 a ²( u. )

.

Математика

G слое будем использовать верхний индекс (+1), а на предыдущем - верхний индекс (-1), на сле

Г 1 I дующем полуцелом временном слое - I +— I, а на предыдущем полуцелом временном слое -

^^^^^^^в

— | (см. рисунок). Запишем теперь разностные аппроксимации для производных ^i ¹ (0) и 2 7                                                                                                dt

G1 (0): dt dGi-1 dt

(0) = G - - ^G i- ,

т

dG i + 1 ₍₀₎ = G ^; - G i+1 dt             т

•

Окончательно расчетная формула приобретает вид

- ² a ² ( и ) _т

G , ( ⁺¹⁾ = ( G i - B ) e h ²    + Ат + B ,

где A = — G, 2 т    i

i - 1      G i - 1    ⁺ G i + 1      G i + 1

, в = G -'⁺ G -+ 1 - A4-

2           2 a ²( u i )

•

Для расчета значений функции G на временном слое t = т , а также для вычисления значений функции в полуцелых слоях по времени можно воспользоваться формулами:

- ² a ²⁽ U i )

G i (T ) = G i e    h ²

I+ 1 )    — a2M

G i ² = G i e   h

2 a ² ( u i )

1 - e" ^{h 2}

1 - e

a ² ( u i ) h'

G i - 1 ^{+ G} i+1

2       ,

G i-1 ⁺ G i+1 2

.

Для применения формул (5)-(7) необходимо по данному значению Gi найти температуру ui та-ui кую, что Gi = J q (О d^- В силу монотонности функции G (и) эту задачу можно решить методом 0

деления отрезка пополам (дихотомии).

Аппроксимация краевых условий

Для выполнения краевых условий введены фиктивные узлы с номерами 0 n N + 1 (см. рисунок ): сначала рассчитываются значения искомой функции во внутренних точках, после чего исходя из краевых условий задаются ее значения в фиктивных узлах.

Перепишем краевое условие на левом конце в задаче (1) с учетом замены искомой функции:

д G д x

x = 0

= Д ( и (0, t )) (6 - и (0, t )) + Q i .

д G

Обозначим через G 1 функцию, обратную к функции G, производную — дx аппроксимируем x=0

„           д G разделенной разностью — дx

-

x = 0

1----0, а значение G(0, t) - полусуммой G(0, t) = —°----1. То- h                                                  2

гда условие (8) может быть записано в виде

2 G 1₊2 _{г г}

---1--- G G h h (

■ -1

г -1 1 ^G 0 ^{+ G} 1 I L Г)

⁶ i ^{- G} III ⁺ Q i .

i V ²    77

Геренштейн А .В., Хайрисламов М.3.

Обозначив z = G ¹ ^ ⁰ + ^ J, из (9) получим уравнение относительно z :

² ■ G ( z )- A , ( z )( 9 , - z ) = 2 G + Q , .                            (10)

hh

Считаем, что функции q (u), c (u), A, (u) и Ar (u) заданы таблично на некотором конечном множестве точек оси температур. Пусть это множество точек есть множество чисел {z1 = 0, z2,..., zm}. Для вычисления функций в остальных точках температуры используется ку-сучно-линейная аппроксимация. Поэтому уравнение (10) на каждом промежутке [zt; zt+1 ], i = 1, m -1 является в общем случае квадратным. Несложные выкладки позволяют записать его в виде

Az ² + Bz + C = 0,                                 (11)

где

A = q ( z i + 1 )- q ( z i ) + A i ( z i + 1 )- A i ( z i ) ( zt + 1 - zt ) h          zt + 1 - zt 2 q ( zt ) zt + 1 - q ( zt + 1 ) zt    A i ( zt + 1 ) - A i ( zt )     , A i ( zt ) zt + 1 - A i ( zt + 1 ) zt B = ■                        ■                    9 i +                         , h         zi + 1 - zi               zu + 1 - zi                   zu + 1 - zi C = ^/ zi q ( f ) d^ - q ( z i ) , i + q ( z - + 1 > - q ( z i ) A 1 - A l (- " i >- " i + - A ( z i * ' )" i 9 , -^ G 1 - Q l . h V 0                           z i + 1 - z i      2 1           z i + 1 - z i                h

Если z* - корень уравнения (11), принадлежащий промежутку [ z i ; z i ₊₁], то искомое значение G ₀ в фиктивном узле с номером 0 будет равно

G ₀ = 2 G ( z *) - G 1 .

Рассуждения для правого конца стержня аналогичны.

Результаты численных расчетов

Для проведения расчетов взята следующая третья смешанная задача:

с (u) It=тт (q (u) AT ^,        0 < t ^ T, 0 < x < L, d t dx V    dx )

u ( x , 0) = ф₀,

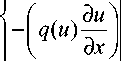
= Ai(u(0, t))(9, - u(0, t)) + Qi, x=0

^f q ( u )| u )    = A r ( u ( L , t )) 9 - u ( L , t )) + Q r ,

[V     dx V x=L где T = 100 c, L = 1 м, ф0 = 22 °C, 9, = 1400 °C, 9r = 1400 °C, Ql = 105Дж/(м2с) , Qr = 0 Дж/(м2с), а функции c(u), q(u), Al (u) и Ar (u) заданы в табл. 1.

Таблица 1

Значения входных параметров задачи, являющихся функциями температуры

Параметр	Температура, °C
	0	100	200	300	400	500	600	700	800	1000
c ( u ), 106 Дж/(м3 ■” C)	3,414	3,568	4,040	4,347	4,812	5,272	5,886	7,286	7,218	7,218
q ( u ), ,'t v C)	22,5	23,4	24,8	26,7	27,2	27,7	28,1	28,6	27	27
A , ( u ), Дж/(м2^ о ° С)	100	100	110	120	130	140	150	160	170	170
A r ( u ), Дж/(м2^ с^° С)	100	120	130	140	150	150	150	150	150	150

Математика

. 2.,

• (12)               ,,

,                               ,                                                                                             ,-

[3, 5].

Таблица 2

Максимальная относительная погрешность решения в сравнении с решением по чисто неявной схеме

	τ ,
N	0,01	0,05	0,1	0,5
40	4,7 ⋅ 10 - 4	4,5 ⋅ 10 - 4	1,52 ⋅ 10 - 3	1,72 ⋅ 10 - 3
60	1,12 ⋅ 10 - 3	1,12 ⋅ 10 - 3	1,19 ⋅ 10 - 3	2,18 ⋅ 10 - 3
80	9,9 ⋅ 10 - 4	1,0 ⋅ 10 - 3	1,06 ⋅ 10 - 3	2,15 ⋅ 10 - 3
100	7,5 ⋅ 10 - 4	7,7 ⋅ 10 - 4	8,7 ⋅ 10 - 4	2,25 ⋅ 10 - 3
150	4,2 ⋅ 10 - 4	4,7 ⋅ 10 - 4	5,9 ⋅ 10 - 4	2,43 ⋅ 10 - 3
200	2,7 ⋅ 10 - 4	3,4 ⋅ 10 - 4	5,0 ⋅ 10 - 4	2,67 ⋅ 10 - 3