Явные выражения давления в акустических волнах, многократно отражённых от поверхностей отражателей канонической формы

Введение. В архитектурной акустике помещений используются цилиндрические и сферические отражатели (например, своды зданий и помещений). Вогнутые части таких отражателей допускают многократное рассеяние звуковых волн. Как правило, при численных расчётах неплоские граничные поверхности отражателей заменяются набором плоских граней вписанных или описанных многогранников, что, конечно, искажает истинное звуковое поле. Особенно это заметно при многократных отражениях волн. В настоящее время работ, посвящённых этой проблеме, сравнительно мало. В [1] рассмотрено двукратное отражение волн от двух круговых цилиндров (в рамках двумерной задачи), а в [2, 3] — от сферических отражателей (пространственная задача).

Поэтому исследование многократного рассеяния высокочастотных волн на поверхностях пространственных отражателей и их скоплений имеет как теоретическое, так и практическое значение в прикладной акустике. В [4, 5, 6] разработан общий подход к исследованию проблемы многократных отражений высокочастотных волн в рамках геометрической теории дифракции (ГТД) на основе дифракционных интегралов физической теории дифракции Кирхгофа. В данной работе общая теория применяется для отражателей цилиндрической и сферической формы.

Постановка задачи. Рассмотрим вписанный в окружность правильный 2 N -угольник в бесконечной акустической среде. Пусть из точки x ₀ , находящейся на продолжении одной из сторон данного 2 N -угольника, от точечного источника давления падает высокочастотная монохроматическая акустическая волна (зависимость по времени e ^{- i ω t} , ω — частота колебаний). Она падает на вогнутую часть граничного контура акустически твёрдого отражателя в виде полуокружности по прямой, на которой находится выделенная сторона многоугольника (рис. 1, 2). На полуокружно-

Работа выполнена при поддержке внутреннего гранта ЮФУ, номер проекта 21301-24/2013-76.

сти находятся N вершин многоугольника у * , у 2 , ..., y*_N , которые в ГТД являются точками зеркального отражения волны. При такой траектории многократно отражённого луча луч, приходящий в точку приёма x_{N + 1} из последней точки зеркального отражения y* _N , будет параллелен исходному падающему лучу. При этом будем рассматривать случай, когда расстояние L ₀ от источника x 0 до первой точки зеркального отражения у * и расстояние L N от точки y* _N до приёмника x_{N + 1} равны между собой (рис. 1, 2).

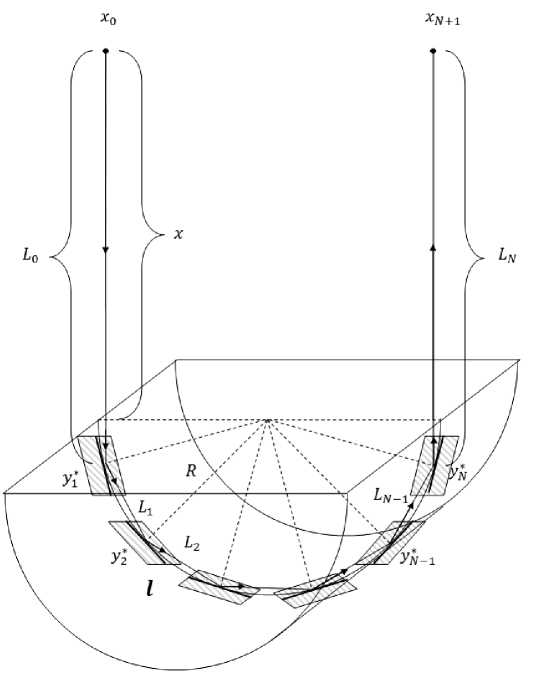
Рис. 1. N -кратное отражение высокочастотной акустической волны от граничного контура твёрдого препятствия в виде вогнутого полуцилиндра

После отделения временного множителя в волновом уравнении задача сводится к исследованию амплитуды давления рассеянного поля. При этом точечный источник, находящийся в точке x ₀ , порождает в точке y пространства давление

P in ( У ) = x о — У | ^e ^x P ( k\x о — У |) , и в двумерном случае: p in ( у ) = x 0 - у exp ( ikx 0 - у |) , где k = ш / c — волновое число и c — скорость акустической волны.

Анализ проблемы проводится в рамках плоской задачи многократного переотражения волны от вогнутой части полуокружности радиуса R и пространственной задачи при той же плоской траектории луча в сечении, перпендикулярном образующей кругового цилиндра (рис. 1) и в диаметральном сечении сферического отражателя (рис. 2).

Цель исследования — выписать явные аналитические выражения амплитуды давления в точке приёма волны. Во всех трёх случаях эти выражения связаны с вычислением определителя порядка N (двумерная задача) и определителей порядка 2 N (пространственная).

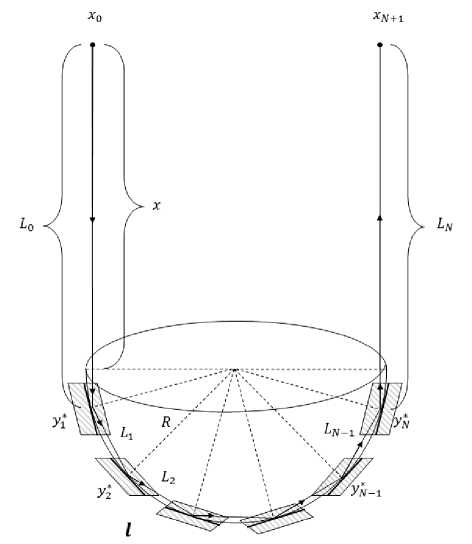
Рис. 2. N -кратное отражение высокочастотной акустической волны от граничного контура твёрдого препятствия в виде вогнутой полусферы

Метод решения. В самой общей постановке двумерная и пространственная задачи об определении давления в акустической волне, переотражённой от скопления препятствий, в случае высоких частот исследованы в [4, 5, 6]. В этих работах на основе модификации физической теории дифракции Кирхгофа [7] получены дифракционные интегралы, главные члены асимптотических разложений которых исследованы методом многомерной стационарной фазы [8]. Полученные аналитические выражения давления в переотражённой волне соответствуют ГТД.

Выпишем аналитические выражения для давления в точке приёма. Двумерная задача [4]:

f Г N     П          ,11

exp V k £ L n +т ( 6 N - N ) [

Р ( x N + 1 )

L L n = o       ⁴              JJ

N

J П L n IIdet ( D N 1

n = 0

Здесь D N = ( d_nm ) , n , m = 1, N — симметричная матрица Гессе со следующими элементами:

dnn = Ln-1 + L-1 - ТТТТГ-Г, dn,n+1 = dn+1,n = Ln, dnm = 0, n * m, n * m + 1, n * m - 1, 6 N = sign DN Pn cosYn и pn — радиус кривизны контура в точке yn контура.

Трёхмерная задача [5, 6]:

f Г N      п exp V k £ Ln +д( 62 N - 2N ) ^

N

Р (xN+1 ) = П cosY n n=1

L L n = o        ⁴

TNA

I П L N I Vl^{det (} D 2 N ¹

V n=0

Lo   lx0   y1\> Ln   |yn   yn+1|, n   1, N   1, LN   |yN

Здесь 5 2 N = sign D 2N — разность между числом положительных и отрицательных собственных значений матрицы Гессе D 2 N = ( d nm ) , n , m = 1,2N , которая является симметричной со следующими ненулевыми элементами d m , n <  m .

Диагональные элементы:

d„ 12„ 1 = ( L ^-11 + L ^-1) ^f 1 - ( q . , L )21 - 2 k ^{( n} ) q , k ), n = 1? N ,

2 n - 1,2 n - 1 \ n - 1        n / I n * ' I 1         1 \ * n ' nJ               * *

dn = L Lh + L ^-1) ^f 1 - ( q n, j_n ¹ - 2 k 2 ⁿ ) q ⁰, k ), n = v n .

2 n , 2 n       n - 1       n              n n             2 n n

Внедиагональные элементы:

d 2 n - 1, 2 n = ^- ( ^L11 ^{+ L} - 1 ) ( q n , i n ) ( q ⁰, ^j n ) , ⁿ = V N ,

- 1      - 0 7 ⁷ 0     7       /7     7

d2n-1, 2n+1 = Ln ((qn , in ) (qn+1, in+1 ) - (in +1, in )) , n = 1, N - 1, d2n-1, 2n+2 = L-1 ((qn , 7 ) (qn+1 , jn+1 ) - (jn+1 , in )) , n = 1, N - 1, d2n, 2n+1 = L-1 ((qn , jn ) (qn+1 , in+1 ) - (^+1, jn )) , n = 1, N - 1, d2n, 2n+2 = L-1 ((qn , jn ) (С1 , L+1 ) - (jn +1, jn )) , n = 1, N - 1.

Здесь k1(n), k2n) (n = 1, N) — главные кривизны поверхностей, а in, jn, kn — орты локальной Декартовой системы координат, определяемой касательными к главным линиям кривизны и нормалями к поверхностям дефектов в точках зеркального отражения yn, n = 1, N . Координаты ортов заданы в некоторой глобальной Декартовой системе координат, qn = {-cos an, - cosen, - cosYn} — направление падения волны в точке yn, а y„ — угол между направлением падения волны и нормалью к поверхности в точке yn.

Отражатели канонической формы. При рассматриваемой траектории плоского луча его параметры определяются соотношениями вписанного в окружность 2N-угольника: . N -1 Yn = п-----, n = 1, N, n 2N ,, ,

Y П = Y * , c = cosy * , L 0 = L N = Rc + x , x e ( - Rc , +* ) , L_n = 2 Rc , n = 1, N - 1.

В дальнейшем будем исследовать величину давления в переотражённой волне в точке xN+1. В случае двумерной задачи из общей формулы (1) следует, что n-1 \-1

|Рокр (Xn+1 )| = f(Rc + X)(Rc)J (|detDOP)|)’2,(3)

det DNкр)=(2Rc)-N det DN,(4)

где D N = ( d nm ) , n , m = 1, N — матрица ленточной структуры со следующими ненулевыми элементами:

d 11 = d NN =- ( 1 + 3z )( 1 + z ) , z = Rcc, z e ( - 1, +» ) , d nn =- 2, n = 2, N - 1;

d n,n + 1 = d n + 1,n = 1, n = 1, N - 1.

Разложением по элементам первой и последней строк вычисление определителя DN0 сводится к вычислению определителей Δn ленточной структуры порядка N -2 и N -3. Определитель Δn порядка n имеет ненулевые элементы Д,, = -2, i = 1, n, Дi i+1 = Дi+1 i = 1, i = 1, n -1 и вычислен методом математической индукции: Дn = (-1)n (n +1).

Для определителя d N окр ) в (3) и давления (4) получаем явные выражения:

N det DNN ок» = 4I- -1-1 z (1 + Nz )(1 + z )-2,

\ 2RC у

V ^Rc\P okp ( ^xn + 1 )| = |^{2 z} ( 1 ^{+ Nz} )| 2 .                                          ⁽⁶⁾

В случае пространственной задачи основу расчётов составляет выражение (2). Первым рассмотрим цилиндрический отражатель (рис. 1). В этом случае

-1                    .,-1

Rc + x ) ² ( Rc ) ^{N - 1} ) (| det Dn" )| ) ²,

где матрица Гессе D . N ") — симметричная, имеет ленточную структуру со следующими ненулевыми элементами:

^d 11 = ^d 2 N - 1,2 N - 1 ; ^d 22 = ^d 2 N , 2 N ;

^d 2 n - 1,2 n - 1 ; ^d 2 n ,2 n ^; n = ² , ^N - ^1;

^d 2 n - 1,2 n + 1 ; ^d 2 n ,2 n + 2 ; n = 1, ^{N 1 .}

Определитель матрицы d 2 цил ) такой структуры равен произведению двух определителей [9], каждый из которых порядка N :

det D 2^циил ) = ( 2Rc )^{- 2} N det D N^ц ) det D N^ц ) .

Причём матрица D N^ц ) совпадает с матрицей Гессе D N двумерной задачи (4), а матрица D N^ц ) = d nn ^), n , m = 1, N в (9) является ленточной со следующими элементами:

d 11 = d nn = 3^, d nn = 2, n = 2, N - 1, d n,n + 1 = d n + 1 n =- 1, n = 1, N - 1.

Значение определителя D N^ц ) получено методом математической индукции: D N^ц ) = 4 ^{z + N} ₂ .

^{( 1 + z} )

Давление \ р_цил ( Xn + 1 )| преобразуем:

| Рцил (Xn+1 )| = [2Rc z (1 + Nz) (z + N )|2 ] .(10)

Для сферического отражателя (рис. 2) давление в переотражённой волне определяется выражением:

-1

I Рсф ( XN +1 )|=(( Rc + x )2 (Rc )N -1 ) (|det D2 N )|) 2, в котором матрица Гессе Ос) имеет такую же структуру, как и в случае цилиндрического отражателя (8). Причём в определителе det О2N) = (2Rc)-2N det О^сф) det DNсф)

матрица d N сф ) совпадает также с D N , а матрица d N ^сф ) = ( d_nm ) существенно отличается диагональными элементами от матрицы d N ц ) :

du = dnn = 1+Z " 2cos2y*, dnn = -2cos2y*, n = 2, N -1, dn,n. = dn+i,n =-1, n = 1, N -1.

Раскладывая определитель det d N ^сф ) (12) по первой и последней строкам, получаем:

det D N^сф ) = G ²A n - 2 - 2 G A n - з + A n - 4 ,                               (13)

где G = ^{1 Z} - 2cos2y * , A = ( - 1 ) ⁿ det D , n = N - 2, N - 3, N - 4.

• 1    + Z             n v/ n

Матрица D n = ( d j ), / , j = 1, n — симметричная с элементами:

• d , = 2cos2y * , / = 1, n , d / , , + 1 = d / + 1, , = 1, / = 2, N - 1.

Следуя [9], det D n = ( sin ( n + 1 ) y ) /sinY.

С учётом этого выражение (13) приводится к виду:

det D N^сф ) = ( - 1 ) ^N - 2 ( sin 2y * ) ^{- 1} [ G ² sin2 ( N - 1 ) y * + 2 G sin2 ( N - 2 ) y * + sin2 ( N - 3 ) y * ] .

Аналитически доказано, что выражение (14) преобразуется к виду: det d N ^сф ) =-- ^{4 z} ^-.

(1 + z)

Определитель матрицы Гессе (12) для полусферы имеет вид:

/   . X N + 1

det D< сф ) = 16 ⁽- ) _2N z ^{2 1 + Nz} ₄ ,

2N       (2Rc)2N    (1 + z)4 , а давление (11) в точке приёма:

_ 1

I Р сф ( x N + 1 )| = ( ^{2 R}c ) ^-1 | ^{Z 2} ( ^{1 + Nz} )|

Остановимся на анализе проблемы замены неплоских отражателей плоскими при многократных отражениях акустической волны. На примере рассматриваемых задач и полученных явных аналитических выражений (6), (10), (15) проведём сравнительный анализ амплитуды давления в многократно отражённой акустической волне от граничных поверхностей неплоских отражателей и от плоских отражателей. Исследуем проблему для системы плоских отражателей, которые располагаются в касательных плоскостях к поверхностям отражателей в точках зеркального отражения У1, У2*, •", yN. При такой благоприятной замене неплоских отражателей плоскими не меняется траектория луча, и изучается влияние на амплитуду переотражённого сигнала только степени искривленности граничной поверхности. Вместе с тем при замене поверхности отражателя плоскими гранями многогранника в общем случае искажаются и траектории лучей. Если траектория луча не изменяется, то в общем случае двумерной (1) и пространственной (2) задач предельным переходом (при стремлении кривизны контура или главных кривизн поверхности к нулю) в определителе матриц Гессе [4, 5] доказано следующее. При любой траектории луча в виде ломаной (плоской или пространственной) линии амплитуда переотражённой N раз волны от системы плоских отражателей определяется выражениями:

( N ) - 2

• •    в двумерной задаче Р пл ( X n + 1 ) = I ^ L n I ,

V n = 0 J

( NY1

• •    в пространственной задаче р (xN t) = ^^.

п"' N ⁺¹/    ^ n-0 n J

Для рассматриваемых отражателей:

- 1

в двумерной задаче             VRcp^ (xN+1 )| = (2 (N + z))"2,(16)

в пространственной                Rc рпл (xN+1 )| = (2(N + z)) 1.(17)

Анализ указанной проблемы сводится к сравнительному анализу выражений (6) и (16) в двумерной задаче и выражений (10), (15) и (17) в пространственной задаче.

Вначале проведём анализ двумерной задачи. Для этого необходимо полное исследование функции f (z)| = |z (1 + Nz)|, z e [-1, + ”), находящейся в знаменателе выражения (6), для дав- ления в переотражённой волне.

На основе полного исследования   f (z )| устанавливается поведение функции

N ^{_ 1} ) U ( - ( 2 N )^{- 1},0 ) ; убывает на множестве

RC р о _крр ( x_{N + 1} )| . Она возрастает на множестве z e ( - 1,

—

z e ( - N 1 , _ ( 2 N ) 1 ) U ( 0, + * ) ; в точке z = - ( 2 N ) 1 имеет минимум: ( 'JRcp p ( x_{N + 1} )| ) = V2 N ; прямые z = - N ^{- 1} и z = 0 являются вертикальными асимптотами.

Это означает, что при расположении источника в точках z = - N ^{- 1} и z = 0 граничный контур отражателя допускает фокусировку акустической волны в точке приёма.

Для пространственных отражателей цилиндрической и сферической формы (см. рис. 1, 2) исследование модуля давлений Rc\pцил (xN+1 )| и Rc\pсф (xN+1 )| осуществляется по той же схеме. Поведение этих величин качественно такое же, что и в двумерной задаче (рис. 3). Интервалы изменения переменной z — те же (рис. 4). Отличие состоит лишь в абсциссах минимумов давлений и их величин.

При z =--

3 N

RP ( X N - 1 )| min = 3^3 N .

N ⁴

При z =---

—

N ² + 1 - N ² - 1

3 N

( z „ t .4^2N )^{- 1} ) Rc|p„ , ( X N + 1 ) „„ ^ 1.

Графики функций величины V Rcp ( x_{N + 1} )| в двумерной задаче и Rcp ( x_{N + 1} )| в трёхмерной задаче для шестикратно переотражённой волны приведены соответственно на рис. 3 и 4.

На рис. 3 и 4 кривые 1 и 3 соответствуют переотражениям волны от системы плоских отражателей, а кривые 2, 4 и 5 — переотражениям волны соответственно от криволинейного контура, цилиндрического и сферического отражателей. Для N -кратно отражённой волны во множестве z e [- 1, - N ^{- 1} ) U ( - N ^{- 1},0 ) U ( 0,1 ) давление в отражённых волнах от неплоских отражателей больше, чем от системы плоских отражателей, а при z e ( 1, + » ) меньше. При расположении источника волны в точке z = 1 ( x = Rc ) давления в отражённых волнах одинаковые. Заметим, что в интервале ( - N ^{- 1},0 ) при N ^ ^ в точках минимума давления имеют по N следующие порядки:

^Rcp„ . ( ^X N . 1 ) min = O ( ! ) ; ^^\Р„ ( ^X N . 1 ) m_b

= O ( V2 N ) ; ^Rc\P сф ( x N , ) „n

= O

⁽^^3 ^N

V

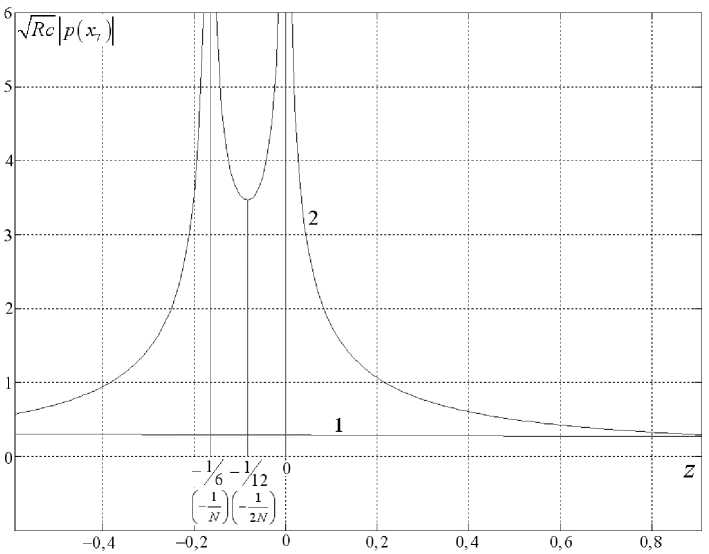
Рис. 3. Влияние удалённости источника и приёмника волны (горизонтальная ось) z = xRc , с = cos 75 ° на амплитуду

давления (вертикальная ось) в акустической волне, шестикратно отражённой от полуокружности RRc р окр, ( x ₇)| (кривая 2)

и системы плоских отражателей RRc р пл ( x ₇ )| (кривая 1)

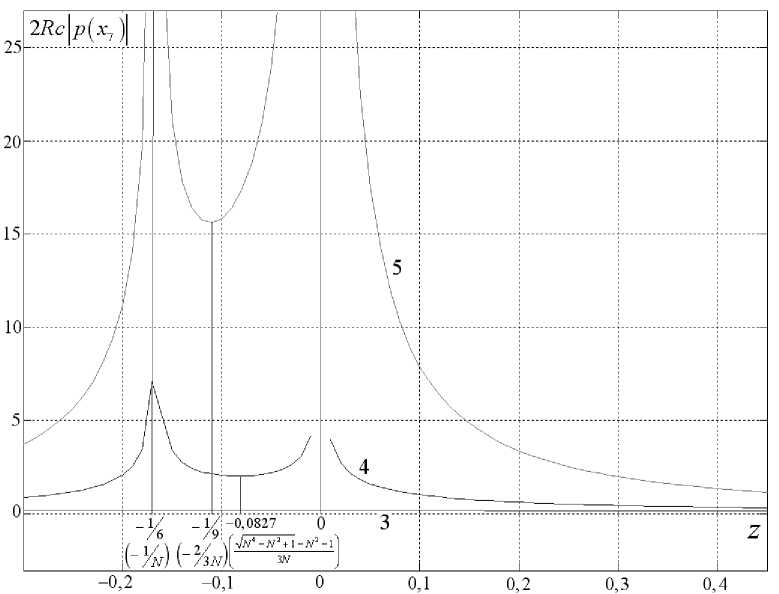
Рис. 4. Влияние удалённости источника и приёмника волны (горизонтальная ось) z = xRc , с = cos 75 ° на амплитуду давления (вертикальная ось) в акустической волне, шестикратно отражённой от системы плоских отражателей 2Rc р л ( x ₇)| (кривая 3), полуцилиндра 2 Rс|p_uил ( x ₇)| (кривая 4) и от полусферы 2Rcp ^ ( x ₇)| (кривая 5)

Заключение. В работе в рамках ГТД получены явные выражения давления в многократно пе-реотражённой акустической волне от вогнутой части кругового контура (6) граничных поверхностей цилиндрического (10) и сферического (15) отражателей. Проведён качественный и количественный анализ полученных выражений в зависимости от расстояний источника и приёмника волны от поверхностей отражателей. На примере многократного отражения высокочастотной акустической волны от поверхностей отражателей канонической формы обсуждена практически важная проблема замены неплоских отражателей плоскими в прикладных задачах акустики.

Заметим, что приложение идей, родственных рассмотренным в данной работе, к распознаванию образа дефектов в упругих средах представлено в работах [10, 11].