Явный вид решения смешанной задачи в анизотропном полупространстве для уравнения Баренблатта - Желтова - Кочиной

Основные положения и уравнения теории нестационарной фильтрации в трещиновато-пористых пластах сформулированы в работе Г. И. Баренблатта, Ю. П. Желтова и И. Н. Кочиной [1], а затем развиты многими авторами [2–4]. Исследование течения однородной слабосжимаемой жидкости в таких средах приводит [3, гл. 3, § 4] к системе дифференциальных уравнений в частных производных

. iE dX j j) + ^a(P2 - P1)=0, +       + с(Р 2 " Р 1 )=0,

где a, b, c — положительные постоянные, зависящие от геометрических характеристик пласта и свойств фильтрующейся жидкости; k ij — тензор проницаемости, определяемый структурой системы трещин; p i = p i (xi , X 2 , X 3 , t), i = 1, 2, — искомые давления в трещинах и пористых блоках соответственно.

Для нефтяных пластов-коллекторов часто характерна анизотропия, связанная либо с естественной слоистостью осадочных пород, либо с развитой системой параллельных микротрещин, вызванных напряжениями в горной породе. Если анизотропия пласта связана с естественной слоистостью, то [3, c. 12–13]

kii = k22 = ko » k = кзз ,    k ij = 0, i = j,

(c) 2013 Умаров Х. Г.

• т.    е. проницаемость k 0 вдоль слоев значительно больше, чем проницаемость k в перпендикулярном направлении, и поэтому направление фильтрационного потока в основном «горизонтальное» [5, c. 323].

В системе дифференциальных уравнений в частных производных (1) перейдем к традиционным обозначениям xi = x, x2 = y, X3 = z. Тогда в случае анизотропного пласта (2) система (1) перепишется в виде dpi   ко dAx,yp1    к d3pi = cko a     + ck d2pi

• _< dt ab dt ab dz ² dt    ab x^,y P1 ab dz² '

k 0            k ∂ ² p 1

• l^p 2 = ^{pi -} ... ^A ■^pi - .. .- 2 -

• где Ax,y = d2/dx2 + d2/dy2 — дифференциальный оператор Лапласа по переменным x, y. Обозначая шо = ко/(ab), ш = k/(ab), хо = cko/(ab), X = ck/(ab) и пренебрегая в первом уравнении системы изменением по времени фильтрационного потока в «вертикальном» направлении, т. е. слагаемым ω ∂∂z32p∂1t , выводим уравнение для определения давления в трещинах анизотропного коллектора (2):

dpi     dAx,y pi            _ д 2 pi dt ш0 dt      X0Ax,ypi   X dz2 ‘                        (3)

В анизотропном трещиновато-пористом коллекторе (2) исследуем фильтрационный поток вблизи одной из границ пласта, например, подошвы, в течение достаточно малого промежутка времени, так что влияние других границ, составленных из охватывающих залежь непроницаемых горных пород, в том числе кровли, еще не сказалось или же несущественно. Тогда искомое распределение давления p _i = p _i (x-y-z-t) def u(x-y-z-t) в коллекторе — полупространстве R + = { (x- y- z) : z >  0 } будет определяться начальным значением давления в момент t = 0 вскрытия залежи:

p i | _t =₀ = u \ _t =₀ = y^(x-y^{,z)- (x-}y^{,z) G R} + ,                         (4)

и краевым условием на границе пласта z = 0:

p i \ _z =₀ = u \ _z =₀ = ^^(x-y^{,t)- (х-}У) ^G R ^{2 -}t ^{G ]0-T[- 0} 6 + ^ ^-           (5)

где число T ограничивает временной промежуток рассмотрения процесса фильтрации. Начальное ^ и краевое ^ данные согласованы между собой: y(x,y, 0) = ц(х,у, 0), (x-y) e R ² .

Решением смешанной задачи Коши (3)-(5) будем называть функцию u(x-y-z-t), непрерывную при (x-y-z) G R ₊ , t G [0-T[, для которой входящие в уравнение частные и смешанные производные непрерывны в области (x-y-z) G R + = { (x-y-z) : z > 0 } , t G ]0-T [; u(x-y-z-t) удовлетворяет уравнению (3) при (x-y-z) G R + , t G ]0-T [, и для нее выполнены начальное (4) и краевое (5) условия.

Функции u = u(x-y-z-t), ^ = y(x-y-z) и ^ = ^(x-y-t) для всех значений «параметров» (z-1) : z-1 > 0 по «пространственным» переменным (x- y) G R ² будем предполагать принадлежащими банахову пространству L _p ( R ² ), 1 6 p < + го , функций f = f (x- y) с интегрируемой по R ² p-ой степенью абсолютной величины, норма которого определяется формулой k f k L p ( _К 2 ) = (JJ R ₂ ^{| f(x-}y^{) | p} d^xdy) ^{i /p} .

В банаховом пространстве Lp(R2), 1 6 p < +ro, оператор Лапласа Ax,y = A с областью определения D(A) = {f G Lp(R2): обобщенная производная Af G Lp(R2)} является производящим оператором сжимающей сильно непрерывной, более того, аналитической полугруппы U(t; А) класса Co [6, c. 261], [7, c. 58], представляющейся сингулярным интегралом

U(t;A)f (x,y) = 4nt jj ^{exp —} ~—^ + ⁽y —~ f (^,n) d^dn-        (6)

R ²

Положительная полуось принадлежит [6, п. 1.1.2] резольвентному множеству оператора Лапласа и для резольвенты (AI — А) ^{- 1} , где I — тождественный оператор, справедлива оценка

^ (AI — A) ^{- 1} f(x,y) ||_M R _{2 )} 6 A k f (х,у_Ж р ₍ r 2 ) , a > 0, f(x,y) e L p ( R ² ),      (7)

и представление степеней [8, с. 664]

+ ^

(AI — A) ^-n f (x,y) = -—L— Г exp( — At) t n^-1 U (t;A) f (x,y) dt, n = 1, 2,...   (8)

(n — 1)! J

o

Введем в рассмотрение два линейных оператора, действующих в банаховом пространстве L _p ( R ² ):

B = x ^{- 1} (I — w o A), D(B) = D(A),

A = xo.w [I — (I — .w A) ^{- 1} ], D(A) = L p ( R ² ).

Тогда уравнение (3) перепишется в виде абстрактного дифференциального уравнения, не разрешенного относительно производной по времени:

B(ut + Au) = U zz , (x,y,z) e R + , t e ]0,T[.                     (9)

Оператор - B является производящим оператором сильно непрерывной полугруппы

U (t; — B ), t >  0, класса C o , которая представляется в виде

U (t; — B) = exp

-

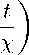
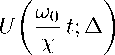
Так как полугруппа, порождаемая оператором Лапласа, является сжимающей, то тип полугруппы U (t; — B) не более — 1/x, ^т- ^e - норма U (t; — B) экспоненциально убывает: k ^U(t; ^—B) k ^{6 ex}p^{( —} t/x), t > 0.

Ограниченный оператор - A порождает сильно непрерывную полугруппу, более того, группу, класса C o , определяемую степенным рядом U(t; — A) = E k =o ⁽ k t A^k , который абсолютно сходится равномерно по t в любом конечном интервале положительной полуоси. Для полугруппы U(t; — A) справедливо представление

+^ k kk xo       xo                            xo       x t t U—t; (I — woA)    = exp--1 > 7 (I — woA) ,

^o /   \wo              /       V  wo / ^,wk k!

/      X                           /             x          /  k=o o откуда, используя (7), получаем ||U(t; — A)k 6 exp ( — ^0 t + ^0 t k(I — woA) 11|) 6 1, т. е. полугруппа U(t; — A) является сжимающей, а, используя (8), для любого элемента f из

L p ( R ² ) выводим представление

[ + ^

/^oZ      / о I xo . А Awexp(—s) ds f + \ —t   I1 2X —ts ]U (swo;A) f----r--- , (11)

^w o             ^w o                    ^s

o где I1(s) = E+^o klck+y (s/2)2k+1 — модифицированная функция Бесселя.

Из формул (10), (11) следует перестановочность полугрупп U ( • ; — B) и U ( • ; — A).

Таким образом, рассматриваемая задача фильтрации может быть сведена к решению начально-краевой задачи (4), (5) для дифференциального уравнения (9) в банаховом пространстве L p ( R ² ), 1 6 p <  + го .

В статье решается начально-краевая задача для дифференциального уравнения, обобщающего (9) в произвольном банаховом пространстве. Затем, конкретизируя банахово пространство и действующие в нем операторы — коэффициенты уравнения, из решения и абстрактной смешанной задачи и оценки нормы ||u k получается решение p 1 рассматриваемой анизотропной задачи фильтрации и его оценка.

• 2.    Постановка абстрактной смешанной задачи

• 3.    Фундаментальное оператор-решение

В банаховом пространстве E рассмотрим однородное дифференциальное уравнение с постоянными операторными коэффициентами ¹

B(u t + Au) = u zz , z G R ++ = { z > 0 } , t G ]0, T [, (12)

где операторы - B , - A являются производящими операторами коммутирующих сильно непрерывных полугрупп класса C q , причем тип полугруппы U(т ; — B) отрицательный: k U(т ; — B ) | 6 M exp( — вт), в > 0; k U(т ; — A) | 6 N ехр(ат), т >  0.

Решение уравнения (12) ищется непрерывным при (z, t) G R ₊ x [0, T [= { z >  0 } x [0, T [ и непрерывно дифференцируемым при (z,t) G R ^ x ]0,T[ по переменной t один раз, а по переменной z два раза. Кроме того, предполагается, что значения решения u принадлежат области определения D(A) оператора A, причем функция и _t + Au принимает значения из множества D(B).

Смешанной задачей для уравнения (12) будем считать, как и в классическом случае, задачу нахождения решения, удовлетворяющего соответственно начальному и граничному условиям u|t=Q = ^(z), z G R+, (13)

u | _{z =Q} = ^(t), t G [0,T[, (14) где ^(z), ^(t) — заданные функции со значениями в банаховом пространстве E , для которых выполнено естественное условие согласования ^(0) = д(0).

Фундаментальным оператор-решением абстрактного дифференциального уравне- ния (12) назовем операторнозначную функцию

^^{Ст; z,t)}   2, п -   ■ U⁽t ^{т ; А)}

U

(z — Z ) ² . ^{4(t — т} ) ’

B

U

(z + Z ) ² . ^{4(t — т} ) ’

B

B ^{1 / 2} , (15)

где Z,z G R ₊ , 0 6 т < t, а положительная дробная степень оператора B определяется по формуле [10, c. 358]

+ ^

B ^v e = —---Г ( [U ⁽£; ^—B) e — е] тдур, ⁰<^v< 1, e ^{G D(B)}. ^{r( — v})                      ^ +

q

Непосредственно из определения (15) следует:

• (I)    оценка нормы

k G(Z,T; z,t)e k 6 M ⁽M '. N B^ exp [a(t - т ) - в(zy^ ² 1, e G D(B ^{1 / 2} );

2 Vn(t - т )          L             ^{4(t - т})J

• (II)    G«,r; z,t)e ^ 0, e G D(B ^{1 / 2} ), при т = t, z или Z ^ 0; или Z = z, т ^ t - 0;

• (III)    представление

  G(Z,т; z,t)e =

  
  

  U(t - т ; - A) 2pn(t - т )

  
  

  U

  
  

  (z - Z ) ² _;

  ^{4(t - т} ) ’

  
  

  _-

  
  

  B

  
  

  z ^z / ( ^{t - T} )

  У   U (s; - B)B ^{3 / 2}

  
  

  e ds

  
  

для элементов e G D(B ^{3 / 2} ) и оценка нормы

1№,т; z,t)e k

MN k B ^{3 / 2}e | Г

2вpn(t - т ) [

zζ

- exp I - pt—

exp

a(t

- т ) - в

(z - Z )²1 4(t - т )J^;

(IV) функция g = G(Z,т; z,t)e, где e G E = D(A) П D(B ^{1 / 2} A) П D(B ^{5 / 2} ), по переменным (Z,т) удовлетворяет уравнению B ( dT - Ag) + dzg = 0, а по переменным (z,t) — уравнению (12); при этом справедлива оценка нормы частной производной

∂g

∂ζ

• ⁶ 4MNk^B G   ^{| z - Z} | ⁺M ^{| z+ Z} | ^exp( ^{- в}т"^" ) ^{exp a(t - т} ) ^{- в} 4z - ^Z\ ; ⁽¹⁸⁾

4vn(t - т ) ^{3 / 2} L                     V t - т/J                  4(t - т )

(V) для всех элементов e ∈ E выполняется равенство

+ ^

B ^{1 / 2} У G(Z,т; z,t)B ^-1/2 e dZ = 0

z ² / [4( t - T )]

U (t - т ; - A)B ^1/2    / U (s; - B) e^s,

πs откуда в силу формулы [11, c. 297] для отрицательных дробных степеней оператора B

+ ^

B ^-v = г^' ) У s ^{v - 1} U (s; - B) ds, v> 0, 0

вытекает предельное соотношение lim t ^t—0

+ ^

B ^{1 / 2} У G(Z,т; z,t)B ^{— 1 / 2} edZ 0

= e.

(z,t) E R +x ]0, T[, 0 6 q < 4 T , где A(t) , A 1 (t) , 7(t) , t E [0,T[, — непрерывные функции. Тогда в каждой точке (z,t) E R + x ]0, T [ имеет место формула

u(z,t) = 21=U (t; — A)B ^{1 / 2} У U (—^ ; - в) — U ((z^; — в) P«) dZ 0

t

⁺ -'   B ^1/2 / U^(t — ^т; — ^A) Uf      Av ^—В^^(т )77

2V n      J                  \4(t — т )     /      (t — т)3 / ²

C Пусть (z,t) — произвольная фиксированная точка из полуполосы R + x ]0, T [ на плоскости (Z,т ), а s — достаточно большое число: s > max { z, 1/z, 1/t } . Внутри полуполосы выделим прямоугольник { (Z,t ) : 1/s 6 Z 6 s, 1/s 6 т 6 t — 1/s } и рассмотрим в нем тождество

{ ^d 2 G⁽0^{T Z,t)} + B ^dG(Zg^T_T ^; z^ — AG(Z^ ; Z,t) B - 5^ z ) — G ( Z,t ;z,t)B ^{— 5 / 2} 1 ^d) — B ^dudT-^T) + Au ( Z,t ) } = 0,

где G(z,t; Z^ ) — фундаментальное оператор-решение (15).

Проинтегрируем обе части тождества (23) по выделенному прямоугольнику, предварительно представив левую часть (23) в виде дивергенции. Тогда получим

t — 1 /s

У ^G z (s, т ; z, t)B ^{— 3 / 2} u(s, т ) — G(s, т ; z, t)B ^{— 3 / 2} u ^ (s, т )] dT 1 /s

+

t — 1 /s

/ g(- , т; z,1 \ b ^—3/2 u z ^s

1 /s

s

G ζ,t

1 /s

— -; z,t\B ^{1 / 2} uyZ,t —

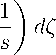
t - 1 /s

g(z, 1; z,t )B ^{— 1 / 2} u( z, 1) dz + [ G _z ,т ; z,MB3³²²n( ¹ ,т) ssss

1 /s                                                  1 /s

s

-J

dτ.

Используя неравенства (18), (17), оценим первый интеграл (обозначив его J 1 ) из левой части (24):

k J1 k 6

t - 1 /s

M(M '  N /  [ [СТА) s + M^ ) exp (qs 2 ) + П В — 1 У 7*/)

2Vn 1  7  L\t — т evr) ^v               s ⁵

1 /s

x exp

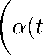
— т) — e

(z—J^ ^{4(t — т} )

A dт )

7 Vt— т J

6 M(M + 1)Ny^ max {1; exp(at)}

x <  max 14T т e [0 ,t ]

А(т) + M^¹^

4 T

s^e — 4hT —

zβ

V в — 4hT J

+ —? max 7(т) exp ( — в es ⁶ т e [0 ,t]             \

(z — s) ² 4T

Аналогично, используя (17) и очевидное неравенство 1 — exp( — у) 6 y, у >  0, и обозначая v = max { 1/2; 5 } , оценим норму второго интеграла J 2 из левой части (24):

II , || „ MNz / /     / „    ,   „(z — 1/s) ² И^{т 1 / 2 A} 1 ^{(т )}e^xp(qs ^{2 ) +} s й^(т)] d^T

" J ² " ⁶ МП J ^exp r^{(t — T) — e} 4 ■ ■ )----------(t — 7) 3 / 2----------

1 /s

+ ^

MNz max { 1; exp(at) }                                Г (   „ (z — 1/s) ² A ,

• - ----------------- max [A ₁ (r) exp(qs ² ) + ^(r)1     exp I — в -----;-----r I dr.

s^{1 v} Vn          т e [G ,t ]                              J V          ⁴       /

1 / V t

Из полученных оценок норм интегралов J i , J 2 следует, что J i , J 2 ^ 0 при s ^ + го .

Далее, используя формулы (19)–(21), покажем, что lim J3 = lim s^ + ^    s^ + ^

s

G ζ,t

-; z,t)B ^1/2 u\ Z,t — s

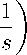
dZ = B ^{1 / 2} u(z,t).

1 /s

Действительно, для любого сколь угодно малого числа е >  0 имеем

II J 3 ^—

B ^{1 / 2} u(z,t) — B ^{1 / 2} u(z,t)

sz ² / 4

+ U fl; —a) -= [ U (r; — B)u(z,t) - r sπ     r

G

- B ^{1 / 2} u(z, t)

U

1_

; s

+

1 /s

A

-; z,t\B ^{1 / 2} uyZ,t --1 — u(z,t)

G ζ, t

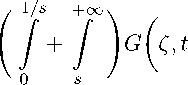
-; z,t)B ^{1 / 2} u(z,t) dZ s

— IB ^{1 / 2} u(z,t)

+

MN π

A(t) exp

dζ

exp( — вг)

dr

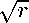
+ M - N exp (^a) (2^1 max

Vn      к sd [ V в I Z I 6 // s

+ ^ ^{a +} qz ²) / sz ² / 4

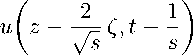
— u(z, t)

(V so +^\                  ,--------- o f , Ml Г ( L 4 Л 2qz V

J ⁺ J n^exp["(V^{е —} s^qZ ..)

- ^     4^80 ' ^V

+ exp

^у ^{в —} —^{qZ +} V^s

4qz +

2qz

— es — 4q

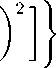
dZ + A(t) exp(qz ² )

, - 4 8 0   V s (1 /s - z ) / 2   . ^        . ^

■ /      /     / - J

-го         ^        у s o    V s ( s - z ) / 2

{ exp(qZ ² ) + exp [ — в(z ^— s + Z ) ² ]} dzj>< е

для всех достаточно больших чисел s g , s: s g < s.

В интегралах из правой части (24) можно переходить к пределу при s ^ + го :

s lim s^+ra

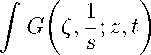
B / ^;   1)

s

^{1 /s}

dζ

= —1= U(t;-A) / [uf (z - Z)2; -b) - U((z + Z)2; -b)L(Z) dZ, 2Vn v ’ J [ V 4t / V 4t t—1/s lim s^+ra

f G 1 ,t ; z,t)B—1/2u 1 ,t ss dζ

1 /s

t z                          z2                  dτ

= 2 ^ Л J U ⁽ t - ^T ; - A) U (4(t - т ); ^{- B})^^(T)(t - т ) 3 / 2 ‘

Отметим, что в последнем случае подынтегральная функция при t = т особенностей не имеет, более того, обращается в нуль.

Таким образом, переходя в (24) к пределу при s ^ + го , получим

B^{— 1/2} u(z,t) = ^U (t; - A) У U (( z^; -в) - U !    4/ 2; -^ ^(Z) dZ

t

+2vnJU(t - т;-A) U.     ; B) (T-^ - откуда и следует формула (22). B

Теорема 2. Пусть значения начального данного ^(z) и краевого условия ^(t) принадлежат множеству E и справедливы оценки норм непрерывных функций ||AB 1/2^(z) k, kB5/2 ^(z)k 6 K exp(hz2), K = const, z E r+, 0 6 h < 4T; kAB1/2 ^(t)|, |B5/2 ^(t)k 6 A(t), t E [0, T[, где A(t) — непрерывная функция. Тогда решение u(z, t) смешанной задачи (12)-(14) в каждой точке (z,t) E R+x]0, T[ дается формулой (22) и для него справедлива оценка нормы ku(z,t)k

M ³ Na_t Г A t ""1^"" [2ve ⁺

(M + 1t)K     / ph ₂

V P - 4hT ^exp Le-lhT z

где a _t = max { 1; exp(at) } , A _t = max _T e [0 , _t ] A(t)-

C Покажем, что норма функции u(z,t), определяемой формулой (22), удовлетворяет оценке (25). Имеем

+ ∞

(z - Z ) 2 4t

(M + 1)Kexp(at) Г           _n

A------ ¹vt        j exp hh( ² - P

+ z j А(т)

- т) - P   ^z 2    t ^dT , I 6

4(t - т ) / (t - т ) ³ / ² J

M ³ Na _t β 2 ^√ _π

|(M + 1)Kexp (hz 2 )

+∞                             +∞ x У exp ^ - (в - 4hT)r2 + 4zhVTr^ dr + zAt J exp ( - Pz2s2) ds >.

-∞                                   0

Откуда, используя значения табличных интегралов в правой части последнего неравенства, получим (25).

Проверим, что функция (22) удовлетворяет уравнению (12). Для этого в силу свойства (IV) фундаментального оператор-решения достаточно показать, что частные производные функции u (z, t) можно вычислять при помощи дифференцирования под знаком интеграла. А это следует из следующих трех оценок норм частных производных:

k U z k =

+ 2Vn

U (t; - A) T\ z + Z U( (z + Z ) ² _;

2 V nt J 2t \   4t ’

-

B

-

z - Z U ( (z - Z ) ² 2t    V 4t

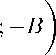
J ^{U (t - T; - A)U}(«t - T)^: - B) B⁾ — 2 ■   ■ B ^{3 / 2} ')

B 3/2^(Z )dZ dτ

(t - т ) ^{3 / 2}

/      + ^                  ( z + ^z ) 2^{/ (4 t )}

MNα t K

^FT /'ph d J (

^{1     0}                     ( z - Z ) ² / (4 t )

M

2 ,^ + \ sJ exp(es) ds

t

MA t Г /M z ²

⁺ T J   ⁺ 2T

В первом слагаемом из фигурной скобки в правой части неравенства (26) поменяем порядок интегрирования и оценим внутренний интеграл; во втором — выполним замену т = z ² /(4s) и увеличим отрезок интегрирования до полуоси:

t

MNa_t 2MA_t MM   A , ds

" u z k ⁶ "VT — / u ^{+ 2s}) ^exP^- - ^вs) v s

K

+ —F t

+ ^

j — + 2s^ exp h(z + 2 V sT) 2 - Ps ds>.

Используя неравенства

+ ^

У s ^m exp( - as ² + 2bs) ds 6

2 m exp(b ² /a) ".

a ⁽ m ⁺ i ^{) / 2}

где a >  0, m — натуральное число, получаем

m/ 2

m + 1 \       / b² \ ^z

2 7 + ^П V "a /

,

(     4K kuz k 6 MNαt

( Vnt(e - 4hT )

M

— (1 + 2zhV nzT)

⁺ в - 4hT V ⁺

8z2h2T r в - 4hT\p - 4hT

π

/ phz² A   2M(M + 1)A_t)

^exp V в - 4hT ) ⁺     M/²    J ‘

+ ^

k u t + Au k =

-

—^U U (t; - A) /

4Vntt         J

(z - Z )². R ^U( ^t^:-^B

-

U (^{-^ :

4t

-

B   B ^{1 / 2} y(Z) dZ

+   /-- о

8 Vnt t ²

+ ∞

и (t; - A) У (z - Z ) ² u

(z^; -в) - (z + Z ) ² u (( z^; -в) b ^{3 / 2} v ( Z ) dZ

z ³ +

3z

-

t

J^U (t

t

/^U (t.

-

-

T ; - A) U^Tif—x ; - b)b ^{3 / 2} ^(t )    d\₅/2

A4(t - t )      /           (t - t )5/²

t ; - a) u\tt+ —г; - в b ^{1 / 2} ^(t ) 4(t - T)

_dτ 5 / 2

^{(t - T})

I 3M /1   4h2Tz2 A x | ПГ V2 + в - 4hT ) +

3M ² (M + 1)Na _t A t _z 2 β 7 / 2

,   8MNK

⁺ t(e - 4hT ) ^{3 / 2} 64h ⁴ T 2z⁴ 1 )

в - 4hT[ ⁺ (в - 4hT )²_

βhz ²

^{at +} в - 4hT )"

3) Частично используя оценки из пункта 2), имеем z , . +^                   (z+Z)2/(4t)

kuzz|| = kB(ut + Au)k 6 ^^J ep a / exp(hZ2) dZ    [   exp(-es) ds tVn     4yt   J                J

0                    ( z - ζ ) ² / (4 t )

+∞                               +∞ exp ^ - вг2 + h (2r —t - zt) 2] r2 dr

+ У exp [ - вг ² + h(z + 2r — t ) ² ]r ² dr J

- z/ (2 ^√ t )

z/ (2 t )

+ zMNa t A t

t

dτ

T7 T 2 ⁺

5MNK

⁶ t(e - 4hT ) ^{3 / 2}

₁    8h2Tz² A /

^{1 +} I - 4hT) exp Г ⁺

t

3M [    /   z ² A dT

— H l^{- в} 47JT 5 / 2

βhz ²

в - 4hT

+

3M (M + 1)Na _t A t

_z 2 β 5 / 2

.

Осталось показать, что функция (22) удовлетворяет начальному (13) и краевому (14) условиям. Обозначим через u ^ (z,t) и u ^ (z,t) соответственно первое и второе слагаемые в формуле (22): u(z,t) = u ^ (z,t)+ u ^ (z,t). Выполнение начального условия (13) следует из следующих оценок: | u _M (z,t) | 6 e M i N a t A t / _z + “ _{4 t} ) exp( - вs) ^ | и (используем формулу (19))

IK(z,t) - ^(z) H = U(t; - A>(z) - ^(z)

z ² / (4 t )

+ U (t; - A) — _п У U (s; - B)B ^{1 / 2} ^(z) — s - ^(z)

+ ∞

+ U( - A [\u

2 Vnt  J

(z - Z )2-

;-B -

u( ⁽z + Z)². в ^U( -S^-•^-B

[в ^{1 / 2} VZ ) - в 1 /V(z)] dZ

+ ∞

II U (t; - A>(z) - y(z)|| + U (t; - A) — n   J U (s; -B)B1 / 2_V(z) — s

z ² / (4 t )

+

—= U (t; - A)   /

π

z/ (2 Vt)

U (r2;

- B) - U

;

-

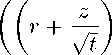
B

x B ^{1 / 2} [у (z + 2r — t) - y(z)] — rr

Первые два слагаемых в правой части последнего неравенства стремятся к нулю при t ^ 0+, т. е. являются бесконечно малыми величинами o(t) при t ^ 0+. Таким образом, для всех достаточно малых t > 0 и любого z Е R^, разбивая область интегрирования на части и оценивая подынтегральные функции, имеем ku(z,t) — v(z)k 6 IK(z,t)k + \\u

+ ^

6 o(t)+ M ⁽Me₂2 - n^^{Na t}   / exp ( - вг ² ) ^ B ^{1 / 2} ^(z + 2r — t) - B ^{1 / 2} ^(z) ^ — rr

- ^z/(2 V ^t)

• ⁶ o^{(t) + M ( M + - 1) Na t} ( j ^ max [^B ^Mz ^{+ 2}r — t ⁾ - B ^{1 / 2} ^^(z)] ^в Vⁿ [V^е | r | 6 ro ^{L                                  J}

  +2K (z + 2r — t ) exp(hz ² )

  

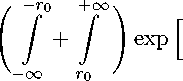
  (в - 4hT ) r ²

  
  

  + 4hz — T | r |

  
  

  ^] dr}

  
  

  < ε,

  
  

где e — сколь угодно малое, а r g — достаточно большое положительные числа.

Выполнение краевого условия (14) следует из того, что функции u ^ (z,t) и u ^ (z,t) - ^(t) стремятся к нулю при z ^ 0+. Действительно,

+ ^     ( z + Z ) 2 / (4 t )

IK^{(z,t) k} =

2 —=U (t; - A) j dZ J'   U(s; -B)B ^{3 / 2} y(Z) ds

⁰        ( z - Z ) ² / (4 t )

z /        ^z 2 ^/(4t)           • \ X                                                                     X

6 MNKa t    2 ^— t [ +z [   ^— Sexp [ - (в - 4hT)s + 4hz ^— TS ] ds

β πt

^{V X} 0          z ² / (4 t) ^{7                                                          7}

и для всех достаточно малых z > 0 и любого t Е]0, T[ ku(z,t) - ^(t)k 6 \u^(z,t)k +

z/ (2 V t )

— П   I U(s² ; - B ) B ^{1 / 2} ^(t) ds

+

—n

z/ (2 vt)

-

IUs

;

- B) B ^1/2 ^(t) ds

+

;/;  / u(^;-a)u(s2;-b) Ib1/2^v - ^) - b 1/2^| d‘ z/(2Vt)

Первые два слагаемых в правой части неравенства представляют собой бесконечно малую величину o(t) при z ^ 0+, а в остальных интегралах разбиваем область интегриро- вания на части и оцениваем подынтегральные функции

1/so llu(z,t) - ^(t)k 6 o(t) + 2max{7V "^П; Nat + 1} ||B1/2^(t) || j exp ( - es2) ds 0

+ — max e se[i/so,so]

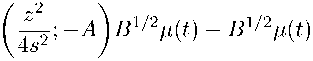
√ _π

• ^                                 z z /J^s0 + ^\

N exp

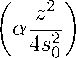
+1

x ||B 1/2^(t) || У exp ( - es2) ds + Me2N at < A J J + j j exp ( - es2) ds s0                                                      0       s0

B ^{3 / 2} д

< ε,

+ — max ^e s e [i /s o ,s o ]

где E — сколь угодно малое, a s o — достаточно большое положительные числа. B

• 5. Оценка и явный вид решения анизотропной задачи фильтрации

Для того чтобы из формулы (22) решения абстрактной краевой задачи (12)–(14) вывести явный вид решения первой краевой задачи (3)–(5), кроме представлений (10), (11) полугрупп, порождаемых операторами - B, - A, необходимо иметь представление дробной степени оператора B. Используя формулу (16), при f (x,y) € D(A x,y ) имеем

B ^{1 / 2} f (х,У) ⁼ 2 ^Т П / f (х,У) - exp ( - X) U (У т ’A x,y )f (х,У) Td^"    (27)

Пусть для K o = const, z >  0, t € [0, T [, m = 0, 3, выполнены условия |^{1 A} X)y ^^(x,y^,z) |¹ L _{p (} R 2 ) ⁶ K o ^exp ^(hz ^{2 )},    |^{1 A} X,y ^^(x,y^,t) |¹ L _{p (} R 2 ) 6 ^A o ^(t),

^A o ^(t) —

где положительная постоянная h удовлетворяет неравенству 4hTx < 1, и непрерывная функция. Тогда выполнены условия теоремы 2, например, с постоянной K = x0x +(3+^0) Ko и непрерывной функцией A(t) = X0x +(1+ш0) Ao(t), и значит по формуле (22) можно выписать решение u(x,y,z,t) задачи (3)-(5), для которого справедлива оценка ku(x,y,z,t)kLp(R2) 6 [XoX2 + (1+ "o)3]

max A(t) + т e [o ,t ]

2K o

V r-4htX

exp

/ hz¹²

V1 - 4htX

Чтобы компактнее записать реализацию формулы (22) в рассматриваемом случае, введем обозначения параметрического множества точек P z на плоскости (x,y): P z = (x,y) + 2(e,n)7" o s ² + ^Ir+ Z^^{> 0} , P z o = P z l s =o , P ₍ ^o = P z l r =o , P^ = P z l s =o ,r =o и вспомогательные функции

Ф( P z ,z,t) = УУ exp( - ^ ²

- n ² ) ^( P z o ,z) d^dn

R ²

+ -|=r^Xo"t / exp( - s ² ) I1 f2s^^{X o} t e ds [[ exp( - ^ ²

Vn\ "o J            V V "o / J J

- n ² ) ^( P z ,z) d^dn,

о

R ²

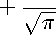
ф( Р е , t, т

+ ^

v Si

>=//

exp( - s ² ) I i

R ²

exp( - £ ²

- n ² ) ^(P e 0 ,t — т ) d^dn

- n ² ) ^^(p z ^,t - ^т) d^dn,

R ²

где Z = z/(2^T). Через Ф(Р0, z,t) и Ф(Р~,t,т) обозначим функции, получающиеся из Ф(Pz, z,t) и Ф^Лт) заменой координат Р^ на соответствующие координаты точки Р^. Тогда из соотношения (22), записанного в виде

u(x,y,z,t) = —^B ^{1 / 2} π

+ ^

- ^{z/ (2} V t )

U (t; - A) U(Z ² ; - B ) ^(x, y, z + 2ZVt) dZ

+ ^

- z/(2Vt)

U(t; - A) U(Z ² ; - B) у (x, y, - z + 2ZVt ) dZ

z

+ 2

t

/ U (t

-

т ;

- A ) U

/     z z ²

V ^{4(t - т})

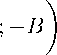
ц(х,У,т ) dT

используя представления (10), (11) и (27), выводим формулу для определения давления жидкости в трещинах пласта:

dζ

X

Ф( P 0 ,z + 2Z ^v',' ) - exp ( - X )Ф( P z ,z + 2Z-At)        + Г

Г 3 / 2                          dr - /

X

у Ф (P ⁰ , 0

z/ (2 V t )

- z ⁺ 2^Z V ^,^t) ^{- exp} ( ^- X ) ^ф( ^p z , - z ⁺ 2^Z V ^t,^t)

r 3 / 2

dr

z

+ 1—9 4n2

t

exp

-

X o ^T ^ o

-

z ² \ dT Г 4тх / т ^{3 / 2} j

Ф (pe ,t,T) - exp (

-

_r 3 / 2

dζ

dr.

Таким образом, имеет место

Теорема 3. Пусть выполнены условия (28) . Тогда единственное решение начально краевой задачи (3) - (5) — давление pi (x,y,z,t) в трещинах анизотропного коллектора (2) — дается в явном виде формулой (30) и для него справедлива оценка (29) .

• 1.    Баренблатт Г. И., Желтов Ю. П., Кочина И. Н. Об основных представлениях теории фильтрации однородных жидкостей в трещиноватых породах // Прикладная матеатика и механика.—1960.— Т. 24, вып. 5.—С. 852–864.

• 2.    Развитие исследований по теории фильтрации в СССР (1917–1967) / Отв. ред. П. Я. Кочина.—М.: Наука, 1969.—546 с.

• 3.    Баренблатт Г. И., Ентов В. М., Рыжик В. М. Движение жидкостей и газов в природных пластах.— М.: Недра, 1984.—211 с.

• 4.    Басниев К. С., Кочина И. Н., Максимов В. М. Подземная гидромеханика.—М.: Недра, 1993.—416 с.

• 5.    Полубаринова-Кочина П. Я. Теория движения грунтовых вод.—М.: Наука, 1977.—664 с.

• 6.    Butzer R. Z., Berens H. Semi-Groups of Operators and Approximation.—Berlin: Springer, 1967.—318 p.

• 7.    Крейн С. Г. Линейные дифференциальные уравнения в банаховом пространстве.—М.: Наука, 1967.—464 с.

• 8.    Данфорд Н., Шварц Дж. Т. Линейные операторы. Общая теория.—М.: Изд-во иностр. лит., 1962.—896 с.

• 9.    Умаров Х. Г. Смешанная задача в банаховом пространстве для аналога уравнения диффузии, не разрешенного относительно производной по времени // Изв. вузов. Математика.—1992.—№ 4.— С. 100–103.

• 10.    Иосида К. Функциональный анализ.—М.: Мир, 1967.—624 с.

• 11.    Красносельский М. А., Забрейко П. П., Пустыльник Е. И., Соболевский П. Е. Интегральные операторы в пространствах суммируемых функций.—М.: Наука, 1966.—500 с.