Эффект насыщения при импульсном возбуждении квантового осциллятора

При взаимодействии интенсивного резонансного излучения с веществом возникают различного рода, нелинейные явления [1], среди которых важную роль играет эффект насыщения. Этот эффект, в частности, приводит к выравниванию населенностей в двухуровневой системе, что ограничивает коэффициент усиления излучения в лазерах [2].

Развитие технологии генерации лазерных импульсов в широкой области изменения длительности, несущих частот и амплитуд поля [3] делает актуальным детальное исследование особенностей их взаимодействия с различного рода мишенями как при умеренных, так и при высоких интенсивностях излучения.

Квантовый гармонический осциллятор (КО) является уникальной физической моделью, для которой существует аналитическое решение при произвольном возмущении.

В этой связи теоретическое рассмотрение возбуждения КО лазерными импульсами с различными параметрами, включая случай высоких значений амплитуды поля, представляется актуальным и интересным.

В данной работе исследуется зависимость вероятности возбуждения квантового осциллятора от длительности и несущей частоты электромагнитного импульса для различных значений амплитуды поля с целью выявления влияния интенсивности излучения на основные характеристики процесса.

2.    Основные формулы

Эффект насыщения при взаимодействии интенсивного резонансного излучения с дипольно-разрешенным переходом рассматривался в классической работе Р. Карплуса и Дж. Швингера [4] для монохроматического поля. Было показано, что форма линии поглощения под влиянием излучения модифицируется и принимает вид (в наших обозначениях)

D(w) х

__________1/72__________

(ш — шо)2 + (1/72)2 + Q2

где шо — собственная частота возбуждаемого перехода, 72 — время поперечной (фазовой) релаксации, По — частота Раби, пропорциональная амплитуде действующего электрического поля.

При импульсном воздействии на двухуровневую систему в общем случае невозможно получить аналитическое решение для отклика на электромагнитное поле.

Выражение для вероятности возбуждения КО между стационарными состояниями m ^ n; [n > т] под действием заданного электрического тока было выведено в работе Дж. Швингера [5]:

m—п       /           I         /       12

w_nm = — (|J |²)     exp (-|J2! /.. ' (|J|²)| ,

здесь J — фурье-образ безразмерного электрического тока, L^Tm-^m — обобщенный полином Лагерра.

Рассмотрим возбуждение квантового осциллятора без затухания под действием электромагнитного импульса вида

Е (t) = E₀f (1,ш_с,т ),                                      (3)

здесь Ео, / (t,ш_с,т ) — амплитуда и временная зависимость электрического поля, ш_с и т — несущая частота и длительность импульса.

Гамильтониан возмущенного КО может быть представлен в виде [6]

Н = Но - ~По/ (^Шс,т ),                              (4)

где Но — невозмущенный гамильтониан КО.

Чтобы получить выражение для вероятности возбуждения КО лазерным импульсом, воспользуемся формулой (2) и соотношением [7]:

здесь

п ^п      . _.

Жю = —г exp(-n), п!

п = QQlF (шо,ш_с,т )|²

— среднее число квантов осциллятора в результате возбуждения.

Пусть лазерный импульс имеет экспоненциальную огибающую (так называемый «двойной экспоненциальный импульс»):

/2exp(t,^c,T) = exp(-|t|/T) COs(Wct).

Тогда с помощью формулы (8) для среднего числа возбужденных в осцилляторе квантов имеем

_        1       П2т2

^П2ехр = 4 [1 + (wq - _Шс)2т ²]².

-

(Ю)

Выражение (10) получено в приближении вращающейся волны, которое применимо для мультицикловых импульсов ( ш_ст >>  1), что здесь и предполагается.

В резонансном случае (ш_с = wq) из равенства (10) следует

п = П2т 2/4,

(И)

т.е. среднее число возбужденных квантов возрастает как квадрат длительности импульса. Можно показать, что такое же соотношение справедливо и для других огибающих импульса, а также для коротких импульсов т <  |ш_с — wq | ^{- 1}.

3. Результаты и обсуждение

Рассмотрим сначала зависимость вероятности возбуждения от длительности импульса (т-зависимость — для краткости) для различных значений частоты Раби, которая является мерой силы возмущения КО электромагнитным полем.

Наряду с размерными параметрами, используем в дальнейшем безразмерные переменные, определенные равенствами

a = шот ; 5 = |шс — wq | /wq; £ = Qq/wq.                         (12)

Таким образом, a — безразмерная длительность импульса, 5 — безразмерная несущая частота и £ — безразмерная частота Раби.

На рис. 1 показана зависимость вероятности возбуждения КО между стационарными состояниями на переходе 0 ^ 1 для фиксированной несущей частоты импульса и различных безразмерных частот Раби.

Видно, что с увеличением параметра £ в т-зависимости вместо одного максимума появляются два. Для слабого возмущения, когда частота Раби удовлетворяет неравенству

Qq < 4Дй|шо — шс| = П2^е,

возникает один максимум при длительности импульса

_   _    1

^ттах — |Ш   Ш |.

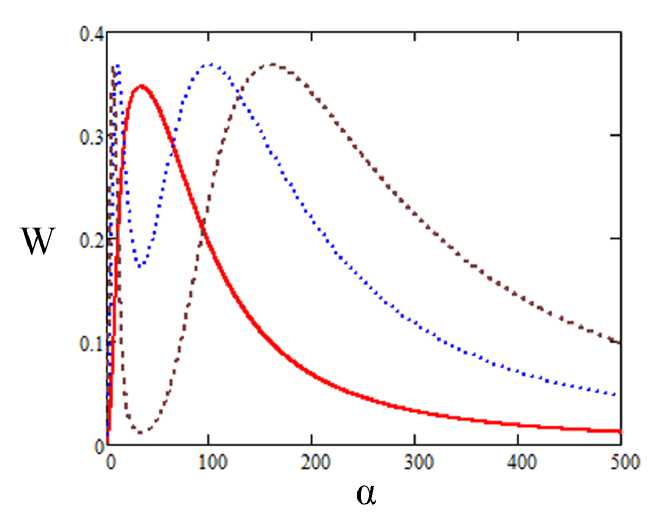
Рис. 1. Вероятность возбуждения перехода 0 ^ 1 как функция безразмерной длительности импульса. для 5 = 0.03 и слслутоших значений безразмерной частоты Раби: сплошная линия — ф = 0.1. пунктирная линия — ф = 0.2, штриховая линия — ф = 0.3

Заметим, что этот максимум исчезает в случае резонансной несущей частоты импульса, когда ш _с = шо-

Для более высоких частот Раби (сильное возмущение), когда.

Qo > Q2e = 4Дй|шо - шс|,

максимум в т-зависимости, положение которого определяется формулой (14), превращается в минимум, и при этом возникают два других максимума на длительностях импульса, равных

Tmax,1,2

Qo ± У^о — 16п|шс — Шо|2 4Дй|шс — шо|2

В пределе Qo ^ |шс — шо| из формулы (16) вытекают следующие приближенные соотношения:

• 2 Дп          Qo

  
  

• ^т1 ~      ; ^т2 ~

Qo         2 л/пІШс — шо|²

Таким образом, характерная частота Раби Qo^e = 4V^l^o — ш_с | разделяет две области с различной качественной зависимостью вероятности возбуждения КО от длительности импульса. Эти две области отвечают слабому и сильному возмущению в случае низких и высоких частот Раби соответственно. В резонансе Q2^e = 0 и имеет место только сильное возмущение, которому, однако, отвечает один максимум в т-зависимости, поскольку тогда Т2 ^ то, как это следует из второго равенства (17).

Рассмотрим теперь зависимость вероятности возбуждения КО от несущей частоты импульса. (спектр возбуждения).

Результаты соответствующего расчета представлены на рис. 2 для перехода 0 ^ 1, фиксированной длительности импульса и различных значений безразмерной частоты Раби ф

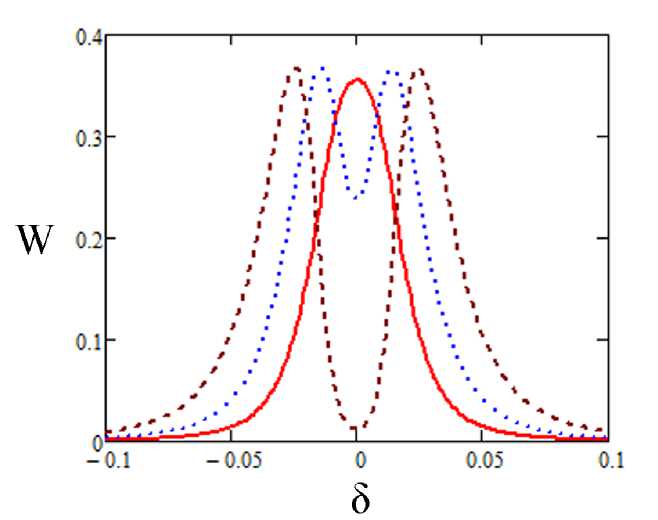
Рис. 2. Спектры возбуждения для а = 50 и следующих значений безразмерной частоты Раби: сплошная линия — £ = 0.035, пунктирна я линия — £ = 0.06, штриховая линия — £ = 0.1

Из приведенного рисунка видно, что для слабого возмущения (низкие частоты Раби), когда

Ио <  2^/т = И⁸₀°\                            (18)

имеет место один спектральный максимум на несущей частоте ш_с = wq. Для высоких частот Раби

Ио >  ^^at

возникает эффект насыщения: центральный максимум превращается в минимум, и появляются два боковых максимума на несущих частотах импульса, определяемых равенством

|wc - Шо|таж

= я

Иот 2Дй

-

Таким образом, при импульсном возбуждении КО характерное значение частоты Раби, определяющей насыщение, дается вторым равенством в формуле (18):

И0^ttt = 2Д^/т.

Эффект насыщения для фиксированной частоты Раби и различных значений длительности импульса демонстрируется графиками рис. 3.

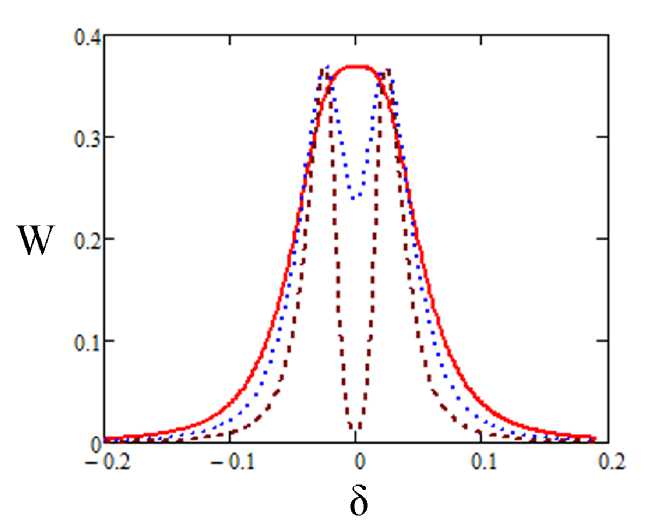
Рис. 3. Спектры возбуждения для £ = 0.1 и следующих значений безразмерной длительности импульса: сплошная линия — а = 20, пунктирна я линия — а = 30, штриховая линия — а = 50

Видно, что с ростом длительности импульса вместо центрального максимума возникает «провал», и появляются два боковых максимума при выполнении неравенства (19).

Отметим, что из формулы (1) следует, что частота Раби насыщения для двухуровневой системы в монохроматическом поле равна

^ tIs = ^ .                             (22)

Сравнение формул (21) и (22) показывает, что в случае импульсного возбуждения квантового осциллятора без затухания роль времени фазовой релаксации играет длительность импульса: 72 ~ т. Это обстоятельство имеет простое физическое объяснение: когерентная связь возбуждающего монохроматического поля и двухуровневой системы определяется временем фазовой релаксации, в то время как в случае импульсного возбуждения осциллятора без затухания продолжительность этой связи определяется длительностью импульса.

Существенная разница в эффекте насыщения для двухуровневой системы и перехода между стационарными состояниями квантового осциллятора заключается в том, что если в первом случае с ростом амплитуды поля населенности уровней выравниваются, то во втором — населенность заданного стационарного уровня уменьшается в пределе сильного возмущения на резонансной частоте (рис. 2,3). Последнее обстоятельство объясняется тем, что с ростом частоты Раби при возбуждении квантового осциллятора в нем происходит перераспределение населенностей между уровнями. Это видно из выражения для среднего числа возбужденных квантов (10), которое неограниченно возрастает в пределе высоких частот Раби, т.е. для больших значений амплитуды электрического поля в импульсе.

4.    Заключение

Таким образом, на основании проведенного исследования можно сделать вывод о наличии двух областей возбуждения КО, разделяющихся по амплитуде электрического поля (частоты Раби) в лазерном импульсе. Эти области — сильного и слабого возбуждения — отличаются количеством и положением экстремумов в зависимостях вероятности процесса от длительности и несущей частоты импульса.

Установлены границы данных областей и получены выражения для положения вышеуказанных экстремумов.

Возникновение рассмотренных особенностей связано с влиянием эффекта насыщения на процесс возбуждения КО. Показано, что данный эффект в рассмотренном случае существенно отличается от своего аналога при возбуждении двухуровневой системы монохроматическим электромагнитным полем. В частности, он проявляется также в зависимости вероятности возбуждения от длительности импульса.

Работа выполнена при финансовой поддержке Российского научного фонда (Соглашение № 22-22-00537).