Эффект перехода от применения бинарных искусственных нейронов к троичным нейронам при совместном использовании пяти классических статистических критериев проверки гипотез нормальности или равномерности распределений малых выборок

В XX в. было создано порядка 21 статистического критерия для проверки гипотезы нормального распределения данных и порядка 24 критериев для проверки гипотезы равномерности распределения данных [1]. К сожалению, все они достаточно хорошо работают только на больших выборках в 200 опытов.

В ряде современных приложений искусственного интеллекта нет возможности иметь столь большие выборки. Так в приложениях нейросетевой биометрии, приложений медицины, биологии, экономики нет возможности использовать большие выборки [2].

В частности, перспективными являются алгоритмы быстрого автоматического обучения больших искусственных нейронных сетей на малых выборках. Первый из этого класса алгоритмов стандартизован в России [3]. Предполагается, что в будущем появится серия подобных алгоритмов [4, 5] и соответствующих им национальных стандартов.

Особый интерес представляют ортого-нализованные алгоритмы быстрого обучения нейросетей, построенные на подборе данных образа "Свой" с нормальным распределением или равномерным распределением [6].

Например, данные на 16 входах нейрона могут быть подобраны при обучении, чтобы иметь нормальное распределение и давать отклик - «0» на выходе нейрона. Тогда, данные на 16 входах этого же нейрона, подобранные при обучении с равномерным распределением, должны давать выходное состояние нейрона - «1». При этом возникает задача надежного нейросетевого распознавания малых выборок объемом в 16 примеров, име- ющих нормальное распределение и равномерное распределение.

Эту задачу первоначально предполагалось решить через некоторое совместное использование ортогональных полиномиальных нейронов Эрмита (для нормальных данных) и ортогональных полиномиальных нейронов Лежандра (для равномерно распределенных данных).

К сожалению, этот путь оказался трудно реализуем из-за того, что искусственные нейроны, построенные на полиномах Лежандра и Эрмита, быстро утрачивают свою ортогональность по мере снижения размеров выборки.

В этом отношении более перспективным является использование искусственных нейронов, построенных на использовании классических статистических критериях прошлого века, построенных для проверки гипотезы равномерности или нормальности малых выборок в 16 опытов [2, 7, 8].

Замена пяти классических статистических критериев XX века эквивалентными им бинарными искусственными нейронами

Для примера возьмем критерий Гири, созданный в 1935 г. [9]. Программная реализация на языке MathCAD формулы вычисления данных по этому критерию приведена в левой части рис. 1.

В правой части рисунка приведены результаты численного эксперимента при воздействии на критерий нормальными и равномерными входными данными малой выборки в 16 опытов.

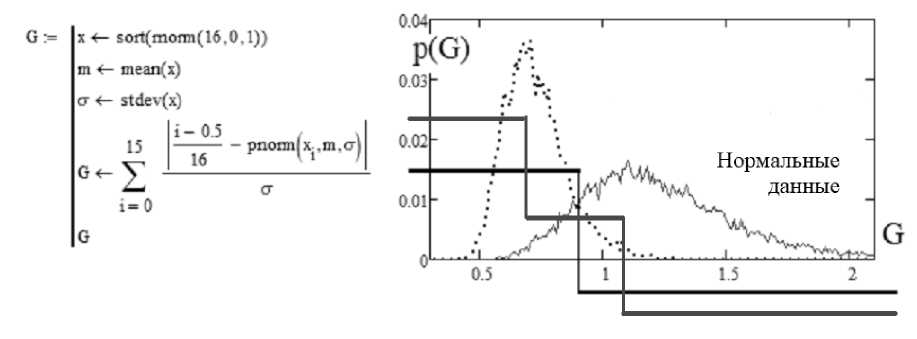
Рис. 1. Критерий Гири (1935 г.) [9], точками отображено распределение данных на выходе сумматора критерия при равномерных входных данных

Очевидно, что данные на выходе сумматора критерия Гири могут быть подвергнуты бинарному квантованию по порогу k=0.81. Отображенный на рис. 1 бинарный квантователь дает состояние «0» при воздействии нормально распределенными данными и состояние «1» при воздействии на искусственный нейрон Гири равномерно распределенными входными данными.

При таком значении порога квантователя ошибки первого и второго рода искус- ственного нейрона Гири оказываются сопоставимы и составляют Р1≈Р2≈РЕЕ≈0.119. То есть, использование только этого нейрона дает решение с доверительной вероятностью 0.88 на выборках в 16 опытов, что недостаточно для практики.

В связи с этим мы можем дополнительно применить критерий Девида–Хартли– Пирсона [10], данные по которому приведены на рис. 2.

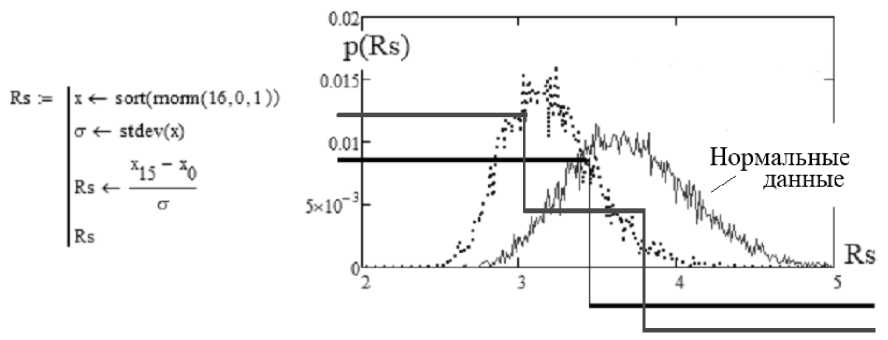
Рис. 2. Нейрон Девида-Хартли-Пирсона, эквивалентный статистическому критерию нормированного размаха (1954 г.) [10]

Из программной реализации этого нейрона (см. левую часть рис. 2) видно, что он вычисляет размах данных, нормированный их стандартным отклонением. В этом отношении приоритет в создании этого типа критериев может оказаться у Херста, использовавшего нормированный размах – R/σ при вычислении своего фрактального показателя [11] уже в начале 20-х годов XX в. В это время англичанин Херст служил в Египте и занимался проблемой статистического предсказания размеров разливов реки Нил. Однако Херст статистически не исследовал фрагмент своего критерия (нормированный размах) в контексте его применения для проверки гипотезы нормальности.

Квантователь нейрона нормированного размаха выполняет сравнение с порогом k=3.41. При таком значении порога квантователя ошибки первого и второго рода Rs нейрона оказываются сопоставимы Р1≈Р2≈РЕЕ≈0.232. То есть, этот бинарный искусственный нейрон работает примерно в два разу хуже, чем предыдущий. Его самостоятельное использование нежелательно, так как обеспечивает доверительную вероятность -0.768.

Следующим рассмотрим критерий Шапиро–Уилка (1965 г.) [12]. Данные по этому критерию отображены на рис. 3.

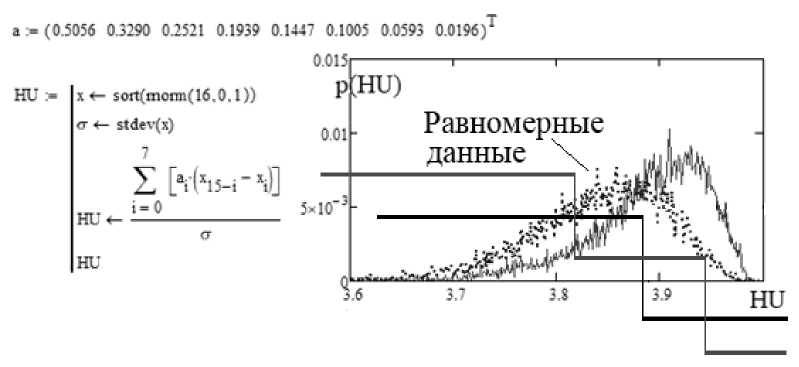
Рис. 3. Нейрон, эквивалентный статистическому критерию Шапиро-Уилка (1965 г.) [12]

Квантователь нейрона HU выполняет сравнение с порогом k=3.81. При таком значении порога квантователя ошибки первого и второго рода Rs нейрона оказываются сопоставимы Р1≈Р2≈РЕЕ≈0.341. То есть, этот бинарный искусственный нейрон работает примерно в три раза хуже, чем нейрон Гири. Его самостоятельное использование нежелатель- но, так как обеспечивает доверительную вероятность - 0.649.

Существенно более высокую достоверность принимаемого одиночно решения обеспечивает критерий Раньи [1, 13] или критерий максимального отклонения данных от центра малой выборки. Состояния этого критерия отображены на рис. 4.

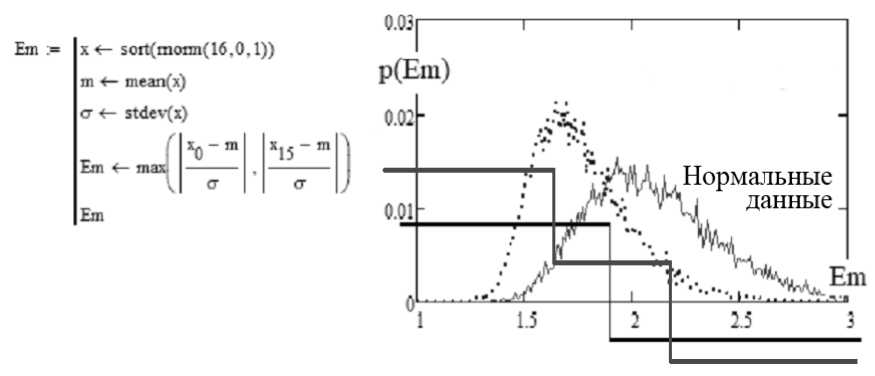
Рис. 4. Критерий максимального отклонения точек от центра (1965 г.) [13]

Квантователь нейрона Em выполняет  Р1≈Р2≈РЕЕ≈0.265, что не позволяет использо- сравнение с порогом k=1.8, обеспечивая вать его самостоятельно.

ошибки первого и второго рода

Самым мощным, из всех рассматриваемых, является критерий Али–Черго–Ревиса (1992 г.) [14].

Статистические данные о выходных состояниях его сумматора приведены на рис. 5.

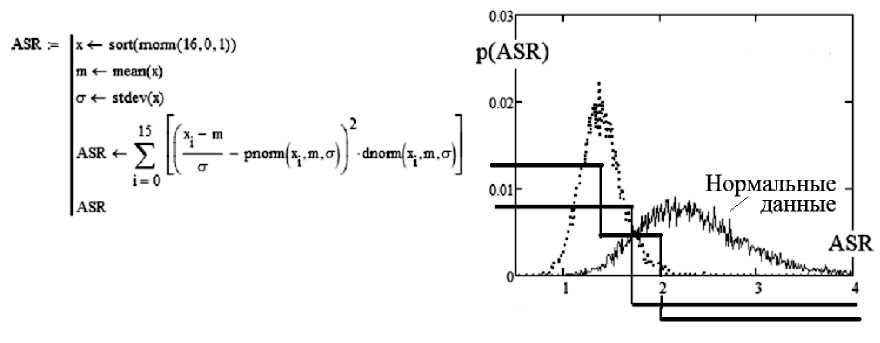
Рис. 5. Критерий Али–Черго–Ревиса (1992 г. ) [14]

Квантователь нейрона ASR выполняет сравнение с порогом k=1.64, обеспечивая ошибки первого и второго рода Р 1 ≈ Р 2 ≈ Р ЕЕ ≈ 0.1, что уже позволяет его применять на практике при допустимой вероятности принятия решений 0.9.

Свертывание бинарных кодов с пятикратной избыточностью при параллельном обнаружении и исправлении ошибок

Так как мы используем однослойную сеть из пяти нейронов, то она будет давать в наилучшем случае состояние «00000», если входные данные нормальные и все пять нейронов примут решение об обнаружении нормального закона [2]. В этом случае с высокой вероятностью мы должны принять решение об обнаружении нормально распределенных данных.

В обратной ситуации, когда все нейроны дают состояние «11111», мы с высокой вероятностью обнаруживаем равномерное распределение входных данных.

Наблюдая коды с пятикратной избыточностью, мы получаем возможность свернуть их, устранив часть ошибок. Самым простым является применение кодов, построенных на подсчете числа состояний «0» в коде. Если код содержит от пяти до трех разрядов с состоянием «0», то все такие кодовые сочетания должны соответствовать обнаружению нормально распределенных данных. Примерно такую же операцию можно выполнить и для первых трех разрядов кода. В этом случае мы будем свертывать коды с трехкратной избыточностью, подсчитывая в них число разрядов «0».

Результат свертывания представлен в левой части рис. 6.

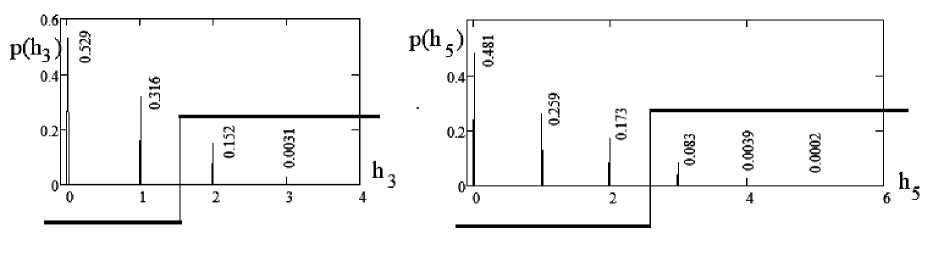
Рис. 6. Спектры амплитуд вероятности расстояний Хэмминга, возникающие при свертывании двоичных кодов с тройной избыточностью и кодов с пятикратной избыточностью

Как видно из левой части рис. 6, устранение трехкратной кодовой избыточности подсчетом состояний «0» (через вычисление расстояний Хэмминга) дает четыре амплитуды вероятности. Наибольшая амплитуда вероятности -0.529 соответствует кодовым состояниям «000».

Все иные кодовые состояния имеют существенно меньшие амплитуды вероятности.

Верные коды, имеющие три и два состояний «0», появляются с вероятностью 0.845. Ошибочные коды с одним разрядом «0» или вообще без состояний «0» отбрасываются с вероятностью 0.155.

Ситуация значительно улучшается, если по той же схеме свертывать бинарные коды с пятикратной избыточностью. Спектр амплитуд линий Хэмминга для этого случая представлен в правой части рис. 6.

Принципиально важно то, что число спектральных линий Хэмминга увеличивается. Как результат вероятность появления ошибок, которые не могут быть исправлены значительно, почти в два раза, снижается до величины 0.88.

Мы видим эффект существенного снижения вероятности появления, обнаруживаемых, но не исправляемых ошибок при росте числа спектральных линий Хэмминга.

Свертывание избыточных выходных кодов троичных искусственных нейронов при параллельном обнаружении и исправлении ошибок в них

Еще одним способом повышения числа спектральных линий Хэмминга является переход от бинарных нейронов к троичным нейронам. При этом накапливающий сумматор искусственного нейрона остается прежним. Отличие состоит только в том, что бинарный квантователь с одним порогом сравнения заменяется на троичный квантователь с двумя порогами для сравнения. В частности, для обогатителя данных критерия Гири (рис. 1) пороги сравнения составляют k 1 = 0.67, k 2 = 1.1. Для критерия нормированного размаха (рис. 2) пороги сравнения k 1 = 3.01, k 2 = 3.91. Троичный нейрон Шапиро–Уилка имеет квантователь с порогами k 1 = 3.79, k 2 = 3.95. Выходные состояния нейрона Шапиро–Уилка отображены на рис. 3.

Все перечисленные выше нейроны имеют по три выходных состояния {«1», «0», «-1»}. Если использовать совместно три троичных нейрона, то мы получаем три разряда кода с тремя возможными состояниями в каждом разряде. Как результат при свертывании избыточности кодов мы получаем шесть спектральных линий Хэмминга, как это отображено в левой части рис. 7.

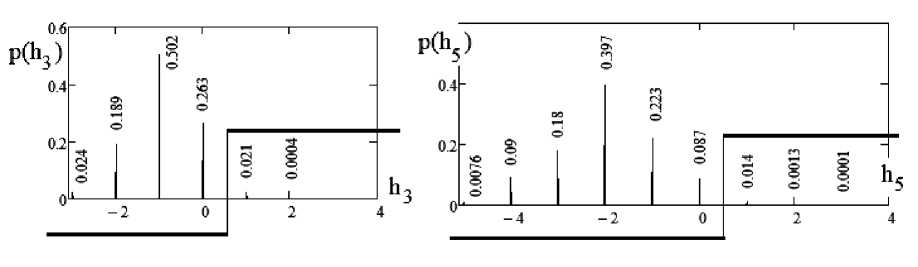
Рис. 7. Спектры амплитуд вероятности расстояний Хэмминга, возникающие при свертывании троичных кодов с тройной избыточностью и кодов с пятикратной избыточностью

Как видно из рис. 7 кодовое состояния {«-1», «-1», «-1»} возникает с вероятностью 0.024. Вероятность появления, следующего симметричного кодового состояния {«0», «0», «0»} составляет 0.263.

Весь спектр кодовых состояний от {«-1», «-1», «-1»} до {«0», «0», «0»} появляется с вероятностью 0.979, а вероятность появления обнаруживаемых, но не исправляемых ошибок -0.0214.

Очевидно, что увеличение длинны избыточного троичного кода до пяти разрядов может быть достигнуто добавлением двух дополнительных троичных нейронов. В частности, может быть добавлен нейрон Раньи, который сравнивает обогащенные данные с двумя порогами k1= 1.61, k2= 2.21. Второй нейрон Али–Черго–Ревиса выполняет сравнение с порогами k1= 1.41, k2= 2.01.

Как видно из правой части рис. 7 число спектральных линий увеличивается с 6 до 9. Это позволяет снизить вероятность появления обнаруживаемых, но не исправляемых ошибок с 0.0214 до 0.014.

Для того, чтобы спрогнозировать характеристики рассматриваемых самокорректирующихся кодовых конструкций при разной кодовой избыточности, следует воспользоваться линейной экстраполяцией в логарифмических координатах. Соответствующие результаты линейной экстраполяции отображены на рис. 8.

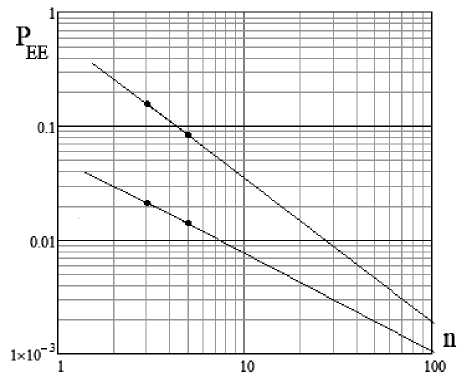
Рис. 8. Прогноз значений вероятностей оши- бок первого и второго рода для двоичных нейронов (верхняя линия) и троичных нейронов (нижняя линия)

Из рис. 8 видно, что решения, принимаемые с доверительной вероятностью 0.99, могут быть приняты только при использовании 280 бинарных искусственных нейронов. То есть в ближайшее время нужно синтезировать 280-21-24=225 новых статистических критериев. С 2012 по 2022 гг. (за 10 лет) усилиями "Пензенского государственного университета" удалось синтезировать примерно 20 новых статистических критериев [15, 16, 17, 18]. При сохранении этой тенденции 200 новых статистических критериев удастся получить примерно через 100 лет.

Ситуация меняется кардинальным образом, если мы от двоичных нейронов перейдем к использованию троичных нейронов.

В этом случае будет достаточно всего девяти троичных нейронов (нижняя линия рис. 8). Таким образом, уже существующих 65 статистических критериев проверки гипотез нормального и равномерного распределения малых выборок вполне достаточно.