Эффект усадки бетона в композитных балках

Shrinkage is time - dependent irreversible deformation which causes the reduce in volume of unloaded concrete due to loss of water. Factors with the most influence on the value of shrinkage strain are the ambient humidity, the dimensions of the element and the composition and quality of concrete.

In composite beams, due to compatibility conditions, shrinkage of concrete part of the cross - section (concrete slab) results in an unfavourable redistribution of stresses. When losing water, concrete tends to shrink, in other words deformation of shortening tends to happen. However, steel part of the cross - section prevents concrete of deforming freely. As a result of restrained deformation, tensile stresses appear in concrete slab. Due to equilibrium, compressive stresses in the steel part of cross - section must appear as well [1].

The aim of this paper is to form a simple numerical model which will sufficiently accurate represent distribution of stresses in composite beam due to shrinkage of concrete slab. Regarding that, comparison between analytical and numerical obtained solution for a different points in time is shown [1-22].

Properties of composite beam

Cross - section of the composite beam consists of the steel part - IPE 400 and the 12 cm thick concrete slab. Based on the expressions given in EC2, creep coefficients which were used to determine the effective Young's modulus of elasticity are calculated [2].

Table 1. Properties of the concrete and the steel part of cross - section

Concrete		Steel
C25/30; f ck [N/mm2]	25	S355; f y [N/mm2]	355
Young's modulus of elasticity E cm [N/mm2]	31 000	Young's modulus of elasticity E a [N/mm2]	21 000
Slab thickness h c [cm]	12	Area A a [cm2]	84,50
Effective width b ef [cm]	300	Moment of inertia I a [cm4]	23 130

Table 2. Properties of the composite beam cross - section in time "t"

Point in time t [days]	7	28	1000	∞
Creep coefficient φ	0	1,2	2,7	3,0
Effective Young's modulus of elasticity of concrete [N/mm2]	31 000	14 091	8 378	7 750
n=E a /E b	6,77	14,90	25,07	27,10
Area A i [cm2]	615,93	326,06	228,12	217,36
Moment of inertia I i [cm4]	78 918	68 347	60 817	59 640

Table 3. Properties of the headed stud anchor

Tensile strenght	f u =450 N/mm2
Young's modulus of elasticity E [N/mm2]	21 000
Diameter Ф [mm]	16 and 25
Height [mm]	100
Longitudinal spacing [cm]	14,6

Construction of Unique Buildings and Structures, 2014, №11 (26)

Analytical solution

Shrinkage is unavoidable in material such as concrete. As it was said in introduction, because the deformation of concrete is restrained it results in tensile stresses in concrete slab and compressive stresses in the steel beam. In other words, composite beam is self - stressed and no external reactions are induced at the supports. The value of these stresses depend on the stiffness of the cross - section. Another time-dependant property of concrete is creep. Creep is time - dependent increase in deformation as a result of sustained stress. The effects of creep are being taken into account through effective Young's modulus of elasticity, in other words by reducing the stiffness of the cross - section. This reduction in stiffness leads to decrease in value of stresses caused by shrinkage.

In a relatively dry ambient the expected value of shrinkage strain of unrestrained concrete slab is 0.03% of the slabs length or higher. However, in composite beam the expected value of shrinkage strain is lower because concrete slab can't deform freely [3].

In Eurocode 2, the expression for determining the value of shrinkage strain are given as a function of the relative humidity (RH), the notional size of the cross - section (h o ), the concrete strenght class and the type of the cement. The total shrinkage strain is composed of the drying shrinkage strain and the autogenous shrinkage strain: [2]

S cs =S cd +S ca ⁽¹⁾

Normal hardening cement CEM 32.5 for a concrete strength class C25/30, relative humidity RH=70% and the notional size of the cross - section h 0 =11,54 cm the values of the shrinkage strain of concrete for which solidification process began after one day (according to Eurocode 4) are given in next table:

Table 4. Values of shrinkage strain

Point in time	ε cd [10-6]	ε ca [10-6]	ε cs [10-6]
t=7 days	15,41	40,56	55,97
t=28 days	24,49	132,55	157,04
t=1000 days	37,43	357,86	395,29
t=to	37,50	375,51	413,01

After the values of the shrinkage strain have been determined, distrubution of stress along the cross -section height for selected points in time is calculated on the assumption of the full shear connection i.e. there is no slip between concrete slab and steel beam. For a given point in time, properties of idealised cross - section are calculated taking into account corresponding creep coefficient. Obtained stress distribution is shown in Figure 1.

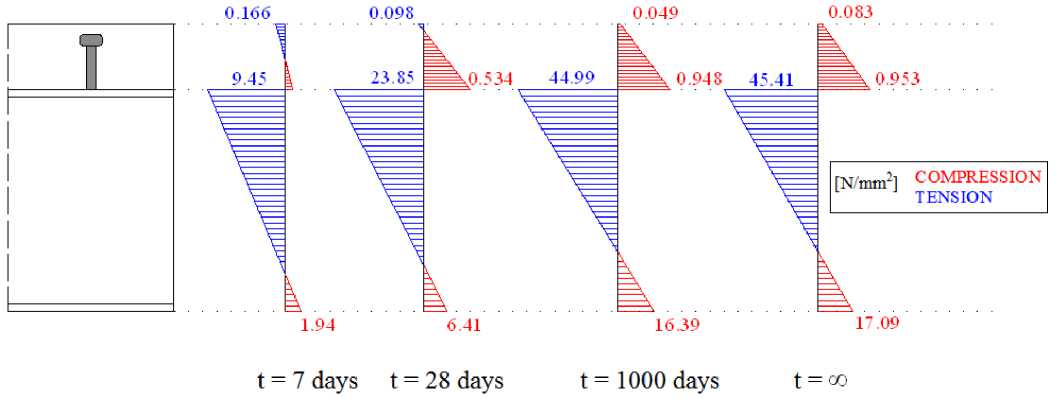
Figure 1. Distrubution of stresses σ x [N/mm²] along the cross - section height

It should be noted that these stresses are only important for serviceability limit state because they cause deflection which can be significant. [3] In ultimate limit state due to plastification, for classes of steel cross -section 1 and 2, the steel beam no longer offers resistance to concrete shrinkage. As a result, the stresses caused by shrinkage of concrete slab disappear.

Numerical model

Following elements were used for numerical model of composite beam:

• -    SHELL elements – rib and flange of steel beam,

• -    SHELL / SOLID elements – concrete slab,

• -    LINK elements – headed stud anchors.

Concrete slab can be modelled with SHELL elements whics have 4 nodes and 4 Gauss integration points or with SOLID elements which have 8 nodes and 8 Gauss integration points. [4] In general, for slabs with simple geometry and constant thickness, as in this model, it is more practical to use SHELL elements. SOLID elements can be used for slabs with complex geometry.

Along the "x" axis, the model is divided into 81 elements and in every node one LINK element which simulates headed stud anchor is associated. Calculation is conducted for linear elastic LINK elements with varying values of stiffness which depend on the diameter of the headed stud anchor. The stiffness of LINK elements for diameters Φ16 and Φ25 mm are determined on numerical model shown in 4.1. Models with finite element mesh are shown in Figures 2 and 3.

In this example because linear elastic behaviour is assumed, headed stud anchors could have been modelled with FRAME elements as well. However, LINK elements were used instead with which eventual nonlinear analysis could be conducted.

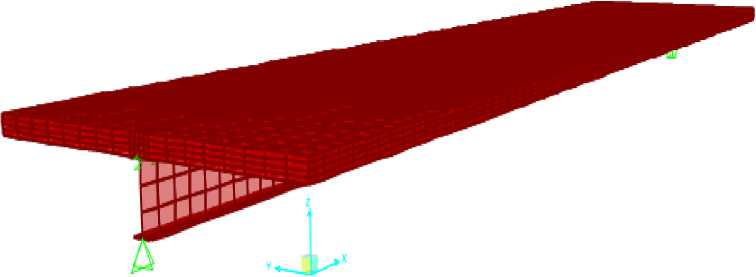
Figure 2. Numerical model – variant I (concrete slab modelled with SOLID elements)

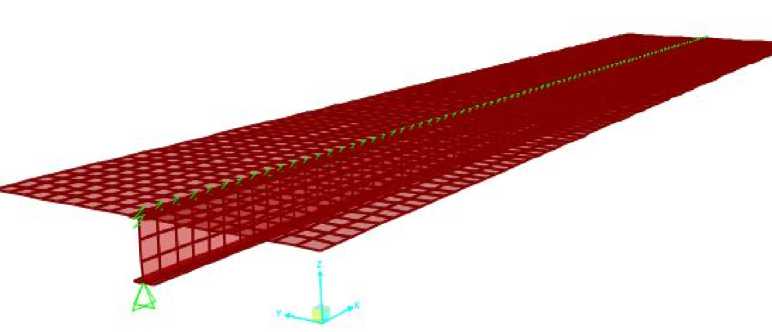
Figure 3. Numerical model – variant II (concrete slab modelled with SHELL elements)

Effects of shrinkage are simulated as a negative temperature load which is needed to cause the appropriate value of total shrinkage strain. Equivalent temperature load is shown in table 5.

Table 5. Equivalent temperature load

Point in time	Shrinkage strain ε cs [10-6]	Temperature [°C]
t=7 days	55,97	-5,60
t=28 days	157,04	-15,70
t=1000 days	395,29	-39,53
t=∞	413,01	-41,30

Stiffness of headed stud anchors

Equivalent stiffness of headed stud anchors is determined on numerical model shown in Figure 4. The length of the composite beam that is being modelled is equal to the longitudinal spacing of the headed stud anchors which is 146 mm. Concrete slab is modelled with SOLID elements while headed stud anchor is modelled with FRAME element. Finite element mesh 14x14x12 (X,Y,Z) is generated. Results are shown in table 6.

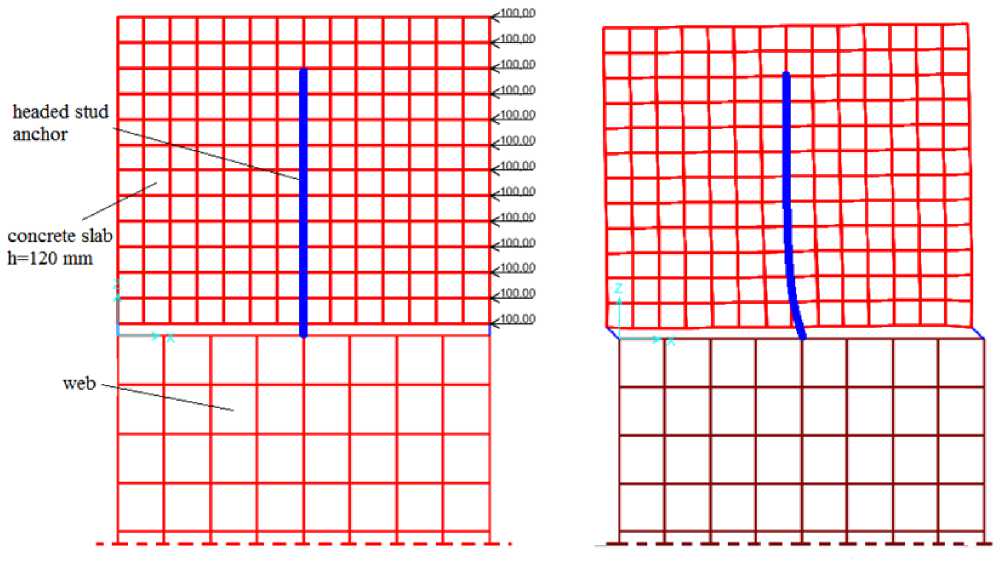
Figure 4. Numerical model for determining equivalent stiffness of headed stud anchor (left) and deformed configuration (right)

Table 6. Equivalent stiffness of headed stud anchor determined on numerical model

Headed stud anchors	Equivalent stiffness [kN/m]
Φ16mm	260 010
Φ25mm	336 500

Comparison of results

Below is given a comparison of analytical and numerical obtained stresses σ x , for headed stud anchors of different stiffness and for different points in time. The comparison is given for the top and the bottom flange of steel beam and is shown on diagrams log t – σ/σ analytical .

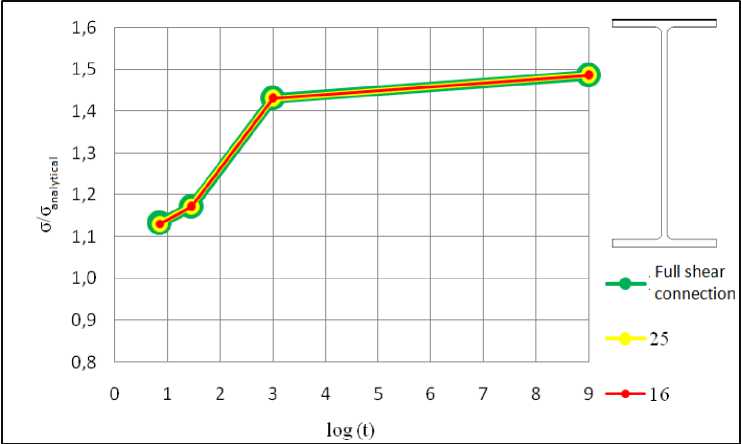
Figure 5. Comparison of numerical model with analyitical solution (top flange)

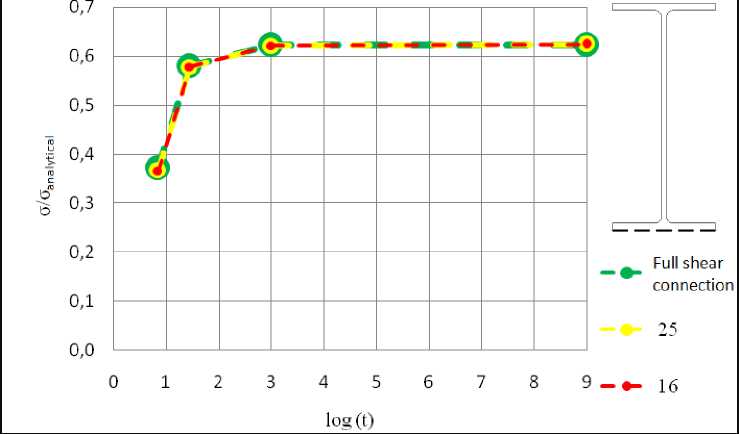
Figure 6. Comparison of numerical model with analyitical solution (bottom flange)