Эффект выбора сетки разносов при прецизионном решении обратной задачи вертикального электрозондирования

*Институт физики Земли им. О. Ю. Шмидта РАН, г. Москва, Россия; e-mail: , ORCID: 0000-0002-9934-0341

Бобачев А. А. и др. Эффект выбора сетки разносов при прецизионном решении обратной задачи вертикального электрозондирования. Вестник МГТУ. 2024. Т. 27, № 1. С. 5–23. DOI:

*Schmidt Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia; e-mail: , ORCID: 0000-0002-9934-0341

Bobachev, A. A. et al. 2024. The effect of spacing grid in the precision solution of the inverse vertical electric sounding problem. Vestnik of MSTU, 27(1), pp. 5–23. (In Russ.) DOI:

Высокая чувствительность электрического сопротивления горных пород к изменениям напряженно-деформированного состояния обусловила широкое использование электрических методов при геодинамическом мониторинге ( Бектемиров и др., 1988; Wilkinson et al., 2011; Богданов и др., 2013; Loke et al., 2014; Supper et al., 2014a, 2014б и др . ). Однако прямые измерения удельного сопротивления горных пород (УЭС) на глубине залегания возможны лишь в исключительных случаях. Измерительные установки вертикального электрозондирования (ВЭЗ) почти всегда располагаются на поверхности, а для расчета удельных сопротивлений решается обратная задача ВЭЗ ( Заборовский, 1963; Якубовский, 1980; Куфуд, 1984; Электрическое…, 1988, 1992; Электроразведка…, 1994; Бобачев и др., 2022г и др . ). Именно по такой схеме проводились измерения сопротивления на Гармском прогностическом полигоне в 1979– 1992 гг. ( Сидорин, 1990 ). Несмотря на то что этот эксперимент был выполнен более 30 лет назад, он до сих пор не имеет аналогов в мировой практике по длительности и точности непрерывных наблюдений, которые выполнялись на протяжении 12 лет ежедневно. Сейсмическая активность района ( Лукк и др., 1990 ) была настолько высокой, что за время наблюдений очаговые зоны местных землетрясений несколько раз захватывали зондируемый объем. Информативная ценность полученных данных возрастает благодаря тому, что на полигоне одновременно проводились другие непрерывные геофизические наблюдения с использованием широкого комплекса методов, что существенно расширяет интерпретационные возможности каждого метода. Вышеизложенные факты в полной мере относятся и к изучению явлений, протекающих в очаговой зоне землетрясения как в период его подготовки, так и после сейсмического события ( Сидорин, 1992 ). Таким образом, исключительное научное значение полученных данных сохраняется до настоящего времени.

Основным результатом эксперимента является набор из нескольких тысяч кривых ВЭЗ, полученных на одной стационарной многоэлектродной установке ( Дещеревский и др., 2017 ). Она включала 12 питающих и 4 приемных диполя с общим центром, расположенных на одной линии ( Дещеревский и др., 2018б, табл. 1, рис. 1). Полученную совокупность кривых ВЭЗ можно рассматривать как профиль ВЭЗ особого типа, каждый пикет которого соответствует определенной календарной дате. С формальной точки зрения, инверсия такого профиля аналогична обработке данных обычных полевых профильных зондирований методом ВЭЗ, с той разницей что любые изменения сопротивлений вдоль профиля будут характеризовать не пространственные вариации УЭС, а изменения сопротивлений во времени ( Бобачев и др., 2020а, 2020б ). Разница, однако, состоит в том, что пространственные изменения обычно имеют достаточно высокую амплитуду, в то время как амплитуда временных вариаций сопротивления быстро уменьшается с глубиной ( Сидорин, 1986; Дещеревский и др., 2004, 2018б ). При этом наибольший интерес с точки зрения мониторинга представляют вариации сопротивления нижних, самых глубоких слоев разреза ( Сидорин, 1986, 1992; Бобачев и др., 2022в, 2023 ). Это определяет особые требования к точности как измерительной установки, так и алгоритма инверсии кривых ВЭЗ.

Использовавшаяся для наблюдений цифровая станция электрического зондирования СЭЗ ( Осташевский и др., 1990, 1991; Сидорин и др., 1996 ) обеспечивала точность единичных измерений сопротивления порядка 0,01 %, однако на практике из-за неизбежных помех фактическая погрешность могла возрастать до 0,1 % ( Дещеревский и др., 2004, 2018а ). Тем не менее эти значения были выдающимися для своего времени и остаются достаточно высокими даже по сегодняшним меркам. Основная неопределенность при восстановлении значений УЭС обусловлена не погрешностями измерений, а точностью решения обратной задачи.

Как известно, обратная задача ВЭЗ является неустойчивой и некорректной. В общем случае ее решение невозможно без наложения некоторых априорных ограничений на модель геоэлектрического разреза ( Заборовский, 1963; Якубовский, 1980; Куфуд, 1984; Электрическое…, 1988, 1992; Электроразведка…, 1994 ). При использовании установки ВЭЗ модель разреза обычно упрощается до одномерной, т. е. среда рассматривается в горизонтально-слоистом приближении. При необходимости могут накладываться дополнительные ограничения (например, фиксируются число и мощность слоев) ( Колесников, 2007 ).

Изначально обратная задача ВЭЗ решалась именно в таком приближении. Однако почти сразу же выяснилось, что широко используемые в традиционной электроразведке алгоритмы инверсии данных ВЭЗ ( Заборовский, 1963; Якубовский, 1980; Куфуд, 1984; Электрическое…, 1988, 1992; Электроразведка…, 1994 ) не обеспечивают ту точность, которая необходима при мониторинге временных вариаций сопротивления ( Сидорин, 1986; Богданов и др., 2013 ). В частности, это было установлено при использовании программы IPI (Induced Polarization Interpretation) ¹ ( Bobachev, 2002 ).

Для преодоления возникших трудностей мы двигались в трех направлениях. Во-первых, наличие 12-летних рядов с сильным сезонным эффектом позволило разработать особый подход к построению базовой (среднемноголетней) модели геоэлектрического разреза. При определении количества и мощности слоев учитывались не только особенности среднемноголетней кривой ВЭЗ и значения сопротивлений, но и амплитуда сезонного хода сопротивления на разных глубинах. Именно по этой причине в верхней части разреза было выделено несколько слоев с минимальным контрастом сопротивлений, но резко отличающейся амплитудой сезонных эффектов. Это позволило наиболее точно отслеживать изменения сопротивлений во времени, включая и сезонный эффект (Дещеревский и др., 2018а, 2018б).

Во-вторых, мы учли, что при мониторинговых исследованиях наиболее интересны не абсолютные значения сопротивлений слоев, а их изменения. В частности, приповерхностные неоднородности искажают кривую ВЭЗ и увеличивают невязку подбора, однако сами по себе интереса не представляют. Это дало основания ввести в данные ВЭЗ так называемую поправку за геологический шум, в результате чего фактическая среднемноголетняя кривая ВЭЗ приблизилась к теоретической кривой ВЭЗ для построенного разреза ( Дещеревский и др., 2017 ). Подчеркнем, что корректировались только средние значения кажущегося сопротивления на отдельных разносах, а все изменения сопротивлений во времени сохранялись.

В-третьих, нами была разработана специальная прецизионная версия программы IPI, учитывающая специфику использовавшейся на ст. Хазор-Чашма установки (заглубление электродов и др.) ( Дещеревский и др., 2017 ).

В совокупности это способствовало уменьшению погрешности решения обратной задачи и невязки подбора почти на порядок по сравнению с обычно используемыми программами ( Дещеревский и др., 2018а, 2018б ). Однако анализ полученных решений (прежде всего амплитуд, фаз и других особенностей сезонных эффектов в разных слоях) позволил обоснованно предположить, что фактические погрешности рассчитанных значений УЭС в действительности значительно превышают те величины, которые можно было бы ожидать при невязках порядка 1 % и менее ( Дещеревский и др., 2018б; Бобачев и др., 2020а ).

Чтобы детально изучить причины возможных ошибок, был построен пакет синтетических профилей ВЭЗ и УЭС, моделирующих возможные сценарии сезонного хода сопротивления различных слоев. Для каждого модельного профиля сначала решалась прямая задача, затем на полученные кривые ВЭЗ накладывался дополнительный шум, аналогичный реальным шумам, после чего решалась обратная задача ВЭЗ и анализировались ошибки решения. В результате было показано, что при малых невязках подбора фактическая ошибка оценки УЭС может на один-два порядка превосходить достигнутую невязку ( Бобачев и др., 2020а ). В такой ситуации величина невязки не должна служить индикатором качества решения обратной задачи. Реальная точность ограничивается так называемым эффектом раскачки сопротивлений – особым видом эквивалентности, проявляющимся в том числе и для того типа разрезов, который характерен для ст. Хазор-Чашма ( Бобачев и др., 2020а, 2020б ).

Для подавления эффекта раскачки разработано несколько алгоритмов регуляризации обратной задачи ВЭЗ ( Бобачев и др., 2020б, 2022а ). Это позволило дополнительно уменьшить погрешность восстановления истинных значений УЭС еще в несколько раз ( Бобачев и др., 2022б, 2022в, 2022г ). Одновременно было замечено, что помимо использования регуляризации точность инверсии можно существенно увеличить при правильном выборе сетки разносов, на которой решается прямая задача.

Традиционно при инверсии ВЭЗ для расчета прямой задачи применяется логарифмическая сетка разносов, согласованная с параметрами фильтра ( Электрическое…, 1988 ). Это позволяет более чем на порядок ускорить расчеты интегрального преобразования Ханкеля, так как один и тот же спектральный потенциал используется при расчетах для нескольких разносов [см. ниже формулы (3) и (4)]. При этом фактические данные измерений (либо синтетические тестовые данные) интерполируются к используемой сетке разносов. Понятно, что такой пересчет может приводить к смещению некоторых оценок.

Поскольку начало расчетной шкалы разносов выбирается произвольно, то одна и та же фактическая сетка разносов интерполируется к расчетной шкале разными способами. В работе ( Бобачев и др., 2022а ) сравнивались результаты инверсии для двух вариантов программы, в которых расчетная сетка разносов [см. ниже формулу (4)] привязывалась к максимальному либо к минимальному разносу экспериментальной установки. Тестирование алгоритма на синтетических данных показало, что эффект сетки разносов может быть очень существенным при прецизионной инверсии. Выбор той сетки разносов, которая лучше соответствует фактическим разносам экспериментальной установки, позволяет значительно уменьшить ошибки решения и подавить раскачку на некоторых границах.

С учетом этого, в следующей версии программы IPI при расчетах использовалась фактическая (полевая) шкала разносов экспериментальной установки ВЭЗ с шестью точками на декаду (см. ниже табл. 3). Это позволило отказаться от интерполяции данных кажущегося сопротивления и выполнять минимизацию непосредственно по измеренным данным.

Основная цель настоящей работы – демонстрация влияния сетки разносов на точность восстановления истинных значений УЭС и амплитуду эффекта раскачки. С этой целью проводится сравнение решений обратной задачи в двух версиях программы IPI: IPI_2020 и IPI_2023. Программа IPI_2020 выполняет расчеты на логарифмической сетке разносов с семью точками на декаду, интерполируя экспериментальные или синтетические данные к указанной сетке, а программа IPI_2023 – на фактической сетке разносов (другие опции, добавленные в программу IPI_2023, при расчетах были отключены).

Материалы и методы

Исходные данные и методика тестирования

Поскольку основная цель работы состояла в максимально точном восстановлении динамики изменений УЭС в нижних слоях геоэлектрического разреза ст. Хазор-Чашма Гармского полигона, методика тестирования оптимизировалась конкретно под данный разрез. Для этого был построен пакет синтетических профилей УЭС, моделирующих экспериментальный разрез ( Дещеревский и др., 2018а; Бобачев и др., 2020а, 2022г ). Все модельные профили включали по 1 461 пикету, каждый из которых сопоставлялся с определенной календарной датой. Шаг между пикетами составлял 2 сут, полная длина профилей – 8 лет, что примерно соответствует реальным рядам с учетом пропущенных наблюдений.

Ранее при обработке данных многолетнего мониторинга различных природных процессов на Гармском полигоне было установлено, что большинство таких временных рядов представляют собой суперпозицию сезонной и фликкер-шумовой (ФШ) составляющих ( Дещеревский и др., 1994, 1996, 1997б, 1999б, 1999в, 2001, 2003, 2021а, 2021б; Дещеревский, 1996а, 1996б; Лукк и др., 1996 ). Данная модель в полной мере применима и в случае кажущегося сопротивления ( Дещеревский и др., 1996, 1997а; 1999а ). С учетом этого, синтетические временные ряды УЭС строились в виде суммы сезонной S 365 и фликкер-шумовой составляющих:

УЭС i ^{( j )} = S 365, i ^{( j )} + ФШ ^{( j )} ,                                                (1)

где i – это номер модели (табл. 1), а j – номер слоя. Всего было построено девять синтетических профилей УЭС, отличающихся фазой и амплитудой сезонной вариации в нижних слоях разреза.

Таблица 1. Фаза сезонной вариации S _{365, i} ^{( j )} в слоях 1–4 для моделей М1–М9 ( Бобачев и др., 2020а, 2022б ).

Значения фазы приведены в сутках относительно сезонной вариации в верхнем слое

Table 1. Phase of seasonal variation S 365, i ^{( j )} in layers 1–4 for models M1–M9 ( Bobachev et al., 2020a, 2022б ).

Phase values are given in days relative to seasonal variation in the upper layer

Модель	Слой модельного разреза
(вариант профиля)	1	2	3	4
М1	0	0	0	0
М2	0	0	=*	0
М3	0	0	0	=
М4	0	9	30	90
М5	0	9	=	90
М6	0	9	30	=
М7	0	9	213	90
М8	0	9	30	273
М9	0	9	=	=

Примечание. *Знаком "=" показаны случаи, когда задана нулевая амплитуда сезонной вариации (нет сезонных эффектов в слое).

Как видно из табл. 1, регулярная (сезонная) составляющая вариаций УЭС задавалась аналогично работам ( Бобачев и др., 2020а, 2022а, 2022б ). Однако в отличие от указанных работ, в настоящей работе уменьшена амплитуда фликкер-шумовой составляющей УЭС (табл. 2). Целесообразность такой корректировки обусловлена уточнением характеристик как экспериментальных рядов УЭС, восстановленных в ходе выполненного цикла исследований, так и шумов, присутствующих в данных кажущегося сопротивления. Из-за этого стохастические различия между моделями уменьшились, что позволяет более точно отследить влияние эффекта сетки разносов на погрешность решения и раскачку для профилей (разрезов), аналогичных разрезу Гармского полигона.

Таблица 2. Базовый геоэлектрический разрез ( Дещеревский и др., 2018а ) и амплитуда сезонной ( Бобачев и др. , 2022б ) и фликкер-шумовой составляющих синтетических рядов УЭС Table 2. Basic geoelectric section ( Deshcherevsky et al., 2018a ) and amplitude of seasonal ( Bobachev et al., 2022б ) and flicker-noise components of electrical resistivity synthetic series

Слой	Мощность	Среднее значение УЭС, Ом ⋅ м	Амплитуда сезонной компоненты УЭС, %	Отношение амплитуды ФШ-компоненты УЭС к амплитуде сезонной вариации УЭС, %
1	1,5	30,0	24	6,27
2	8,7	40,0	3,5	11,62
3	56	30,0	1,2	49,47
4	∝	250,0	2,8	16,37

Процедура тестирования воспроизводила схему, предложенную в работах ( Бобачев и др., 2020а, 2022а, 2022б ):

• 1.    По синтетическим рядам УЭС i ^{( j )} [формула (1)] рассчитывались временные ряды кажущегося сопротивления р a , ip (прямая задача ВЭЗ). Здесь i = 1, .., 9 - номер модели, а p = 1, .., 18 - номер разноса.

• 2.    Для каждого разноса p генерировался шум Noise ^{( p )} , имитирующий реальные шумы экспериментальной установки. При этом мы стремились обеспечить максимальную реалистичность шумов. С этой целью шум Noise генерировался по алгоритму Фосса ( Voss, 1985, 1991 ), причем параметр Фосса ( Дещеревский, 1997 ) подбирался так, чтобы спектральные характеристики синтетического фликкер-шума соответствовали таковым у реальных шумов ( Дещеревский, 1996а, 1996б; Дещеревский и др., 1996, 1997а, 1997б, 1999в, 2003; Бобачев и др., 2022в ). Амплитуда шума задавалась равной амплитуде несезонной компоненты вариаций р k , осредненной по нескольким ближайшим разносам. Кроме того, обеспечивалась коррелированность шумов Noise ^{( p )} на разносах с общими питающими либо приемными линиями, аналогичная таковой для реального эксперимента ( Бобачев и др., 2020а, 2022а ). Полученный шум

• 3.    На следующем этапе для полученного зашумленного профиля р * a , i(p ) решалась обратная задача ВЭЗ, оценивались и анализировались ошибки решения [см. рис. 6 из работы ( Бобачев и др., 2020а )]. Такие расчеты выполнялись для построенных рядов в целом, а также для сезонной и фликкер-шумовой составляющих ( Бобачев и др., 2020б, 2022б ), однако для экономии места в работе показаны только результаты для совокупных рядов.

добавлялся к рядам р a , i(p ) :

р * a ,   p ) = р a, i^(p ) + Noise^0, ) .

Подробнее методика построения модельных рядов р a , i(p ) с наложенным фликкер-шумом описана в работе ( Бобачев и др., 2020а ) (см. рис. 5 из указанной работы), однако для настоящего исследования был сгенерирован новый набор шумов, а их амплитуда немного увеличена по сравнению с процитированной работой.

Инверсия проводилась в двух вариантах: в программе IPI_2020, использующей логарифмическую сетку разносов, и в программе IPI_2023, использующей фактическую сетку разносов. Поскольку целью работы была оценка эффекта сетки разносов, регуляризация, в отличие от работ ( Бобачев и др., 2022а, 2022б, 2022в, 2022г, 2023 ), не использовалась.

Алгоритм инверсии на логарифмической и фактической сетках разносов

Для решения прямой задачи ВЭЗ выполняется численный расчет интеграла Ханкеля p_k ( r ) = Pi r 2 J_o R ( m ) mJ ( mr ) dm,

где r – разнос установки ВЭЗ; J 1 – функция Бесселя первого порядка; R ( m ) называется кернел-функцией и является электрическим полем в спектральной области; m – обобщенная пространственная частота.

Вычисление этого интеграла осложняется наличием осциллирующей и слабо затухающей функции J 1 , бесконечным пределом интегрирования и необходимостью вычисления кернел-функции при большом числе различных значений параметра m .

В настоящее время для расчета кривых электрических зондирований чаще всего применяется метод линейной фильтрации ( Электроразведка…, 1994 ). Исходный интеграл Ханкеля заменой переменных преобразуется в интеграл свертки, который после дискретизации приводится к виду линейного фильтра, позволяющего вычислять кажущееся сопротивление ρ _k :

N pk (r )=Pi E R(mk) Gk, k = 1

где m_k – пространственная частота; G_k – коэффициенты фильтра; N – длина фильтра.

Пространственные частоты зависят от разноса r и растут в геометрической прогрессии. Шаг прогрессии зависит от параметров фильтров и примерно равен 7/10 « 1,39 . Число коэффициентов фильтра N ~ 10–20. Таким образом, расчет одного разноса требует более 10 расчетов кернел-функции. Если использовать сетку разносов с геометрическим шагом, совпадающим с параметром фильтра, то число расчетов кернел-функции сокращается на порядок, так как значения пространственной частоты m_k будут повторяться на разных разносах.

Таблица 3. Фактическая (полевая) сетка разносов установки ВЭЗ на ст. Хазор-Чашма и стандартная вычислительная сетка с семью ступенями на декаду

Table 3. Actual (field) spacing grid of the vertical electrical sounding (VES) installation at Khazor-Chashma station and a standard computational grid with seven steps per a decade

Факт.	3	4,5	6	9	15	25	40	65	100	150	225	325	–	–	–
Станд.	3,0	4,17	5,79	8,05	11,18	15,54	21,59	30,0	41,68	57,92	80,48	111,8	155,4	215,9	300,0

Кривая ВЭЗ всегда достаточно гладкая (углы наклона кривой ВЭЗ не превышают 45 градусов), поэтому пересчет полевой кривой ВЭЗ на новую сетку разносов обычно никак не сказывается на результатах расчета. Особенно если учесть, что типичная точность измерений методом ВЭЗ равна 2–5 %.

Как показано ниже, при прецизионной инверсии подобные манипуляции с данными недопустимы, так как возникающие при этом ошибки уже нельзя считать пренебрежимо малыми. С учетом этого, мы отказались от работы с фиксированной сеткой разносов (табл. 3, строка "Станд.") и перешли к вычислениям на фактической сетке (табл. 3, строка "Факт."), что немедленно отразилось на результатах инверсии (рис. 1). Фактически из процедуры расчетов был полностью исключен этап интерполяции данных к стандартной сетке разносов, привносивший в вычисления дополнительный шум. "Платой" за такое повышение точности инверсии является увеличение времени счета.

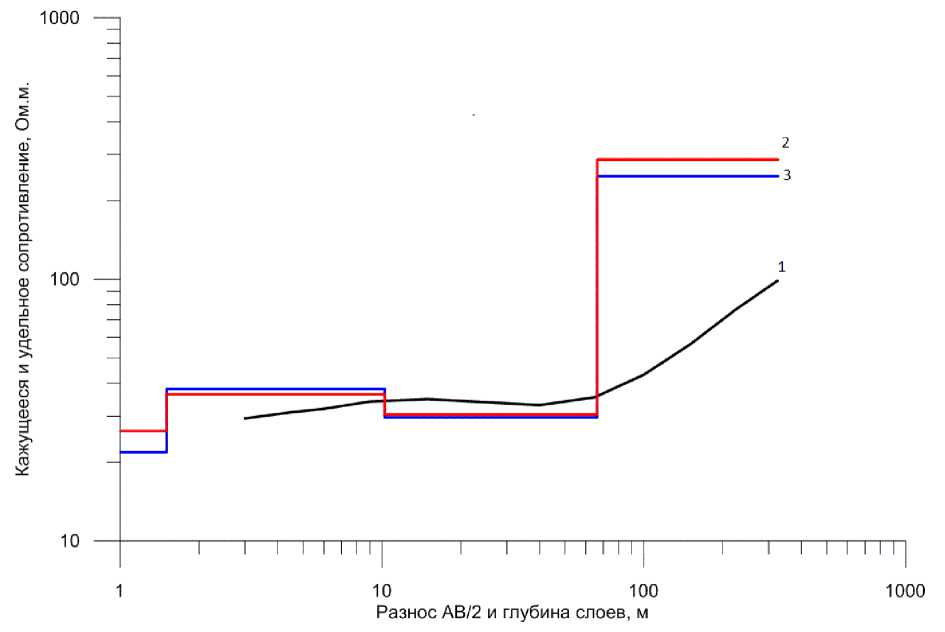
Рис. 1. Пример полевой кривой ВЭЗ (кривая 1)

и две эквивалентные модели, полученные при инверсии по различным сеткам разносов: логарифмическая (кривая 2, красная) и фактическая (кривая 3, синяя)

Fig. 1. An example of the typical VES curve (curve 1) and two equivalent variants of 1D inversion:

standard spacing grid (red) and field data spacing (blue). All thicknesses were fixed before inversion

Результаты и обсуждение

Сравнение результатов для синтетических данных

Примеры восстановленных кривых УЭС для модели М6 приведены на рис. 2. На каждом графике показана исходная (модельная) кривая УЭС, а также кривые УЭС, рассчитанные двумя способами: 1) на логарифмической сетке разносов и 2) на фактических разносах.

Как видно из рис. 2, расчеты в программе IPI_2020, использующей логарифмическую сетку разносов, привели к существенному смещению значений УЭС во всех четырех слоях. Кривая (2) смещена относительно истинных значений УЭС (кривая 1) намного сильнее, чем кривая (3), рассчитанная на фактической сетке разносов в программе IPI_2023.

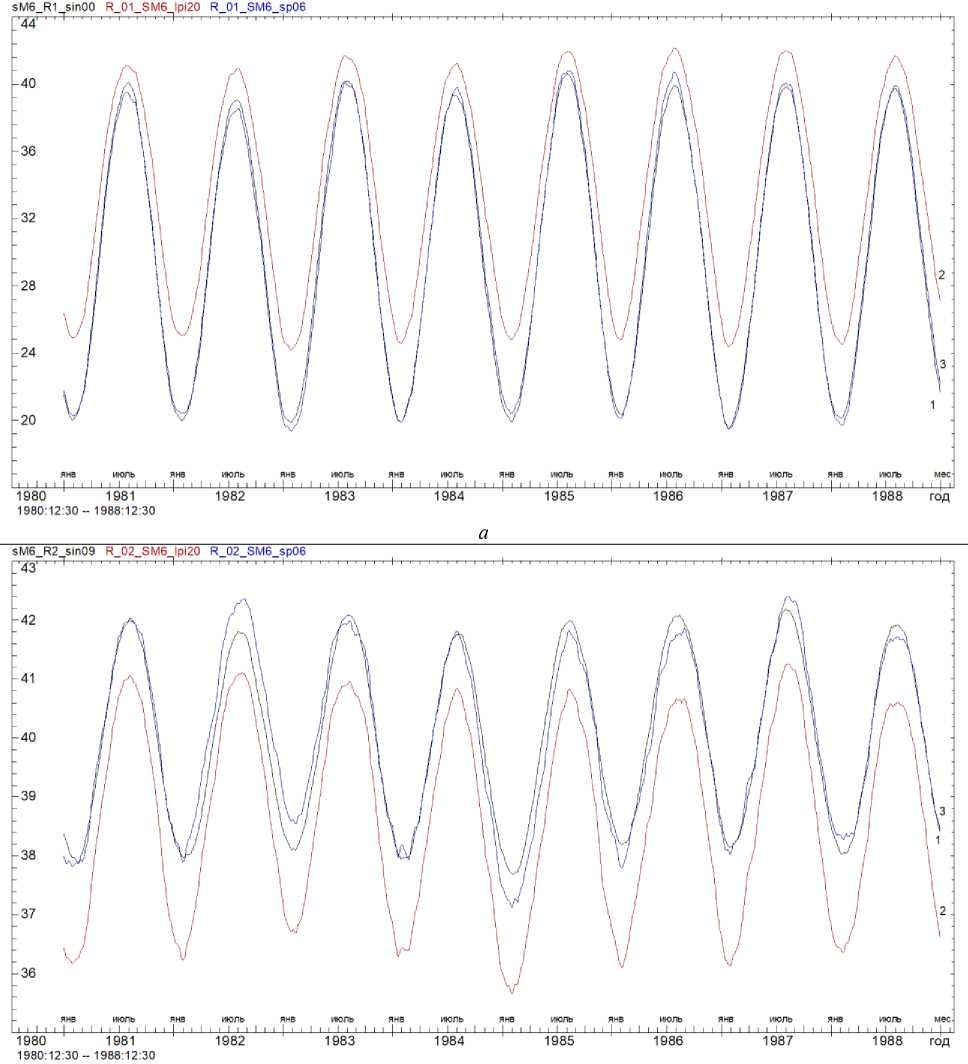
б

Рис. 2. Модельные (синтетические) вариации УЭС (кривая 1) и результат инверсии в программах IPI_2020 (кривая 2) и IPI_2023 (кривая 3) для модели М6: а – слой 1; б – слой 2

Fig. 2. Model (synthetic) variations of VES (curve 1) and the result of inversion in the programs IPI_2020 (curve 2) and IPI_2023 (curve 3) for the model M6: а – layer 1; б – layer 2

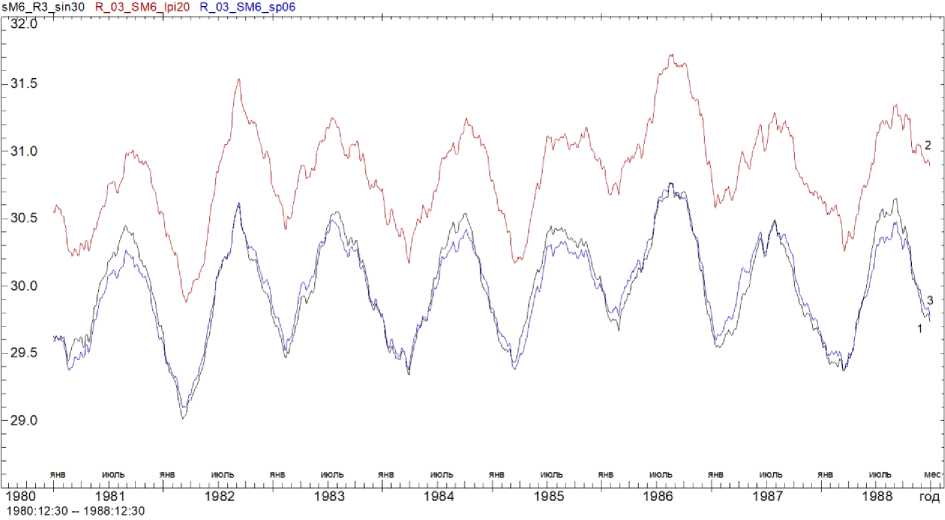
в

г

Рис. 2 (продолжение). Модельные (синтетические) вариации УЭС (кривая 1) и результат инверсии в программах IPI_2020 (кривая 2) и IPI_2023 (кривая 3) для модели М6: в – слой 3; г – слой 4

Fig. 2 (continued). Model (synthetic) variations of VES (curve 1) and the result of inversion in the programs IPI_2020 (curve 2) and IPI_2023 (curve 3) for the model M6: в – layer 3; г – layer 4

Также стоит обратить внимание на рис. 2, г, где показана исходная и восстановленные кривые вариаций УЭС в слое 4. Сезонный ход УЭС в этом слое в модели М6 был задан константой (табл. 1), что показано на рис. 2, г (кривая 1 не имеет регулярной периодической составляющей и представлена фликкер-шумом). Однако несмотря на нулевую амплитуду сезонного хода модельной кривой УЭС, на кривой 2 очевиден мощный сезонный эффект, согласованный с сезонным ходом УЭС в слое 3. При этом амплитуда сезонной вариации в слое 3 занижена по сравнению с истинной (рис. 2, в), а в слое 4 – резко завышена, что приводит к значительной антикорреляции между ошибками решений (табл. 4). Именно этот эффект называется раскачкой сопротивлений (Бобачев и др., 2020а, 2020б). При расчетах на фактической сетке разносов (рис. 2, г, кривая 3) амплитуда раскачки значительно уменьшается, хотя высокая антикорреляция между ошибками решений по-прежнему сохраняется. Несмотря на уменьшение абсолютной величины ошибок в табл. 5 по сравнению с табл. 4, коэффициент корреляции между ошибками решения (который мы рассматриваем как один из основных индикаторов наличия раскачки) почти не уменьшается.

В более формальном виде сводка результатов для девяти моделей приведена в табл. 4 и 5. В каждой строке таблиц показаны результаты инверсии для одной из моделей М1–М9 (табл. 1). В табл. 6 показано отношение ошибок для двух вариантов инверсии.

Заметим, что в отличие от работы ( Бобачев и др., 2020а ) (см. табл. 2–5 из указанной работы) различия между моделями в настоящей работе значительно меньше, что обусловлено изменением характеристик фликкер-шумовой компоненты УЭС синтетических профилей, а также наложенного шума линий. Несмотря на существенное изменение тестовых данных, общие закономерности сохраняются.

Таблица 4. Невязка подбора, средний и максимальный модуль ошибки оценивания УЭС для каждой из моделей 1–9, %. Коэффициент корреляции между ошибками решения (со знаком) в слоях 1 и 2, 2 и 3, 3 и 4 (расчет на логарифмической сетке разносов)

Table 4. Fitting discrepancy, average and maximum modulus of error in resistivity estimation for each of the models 1–9, %. Correlation coefficient between solution errors (signed) in layers 1 and 2, 2 and 3, 3 and 4 (calculation on a logarithmic spacing grid)

Модель	Невязка	R 1		R 2		R 3		R 4		Корреляция ошибок
		Макс.	Сред.	Макс.	Сред.	Макс.	Сред.	Макс.	Сред.	r 12	r 23	R 34
1	0,86	11,92	6,14	2,14	0,78	1,47	0,44	6,78	1,95	–0,60	–0,13	–0,75
2	0,86	11,86	6,10	2,08	0,75	1,49	0,45	7,36	2,19	–0,57	–0,12	–0,74
3	0,86	11,92	6,15	2,17	0,78	1,50	0,45	5,79	1,53	–0,60	–0,15	–0,77
4	0,86	11,97	6,17	2,14	0,78	1,49	0,46	5,92	1,59	–0,60	–0,14	–0,75
5	0,86	11,92	6,13	2,08	0,75	1,51	0,47	6,45	1,80	–0,58	–0,14	–0,74
6	0,86	11,97	6,17	2,14	0,78	1,51	0,46	5,82	1,58	–0,60	–0,15	–0,77
7	0,86	11,86	6,10	2,04	0,73	1,58	0,47	7,01	2,04	–0,56	–0,14	–0,73
8	0,86	11,97	6,17	2,14	0,78	1,52	0,46	6,09	1,74	–0,60	–0,15	–0,72
9	0,86	11,92	6,13	2,08	0,75	1,52	0,46	6,36	1,75	–0,58	–0,14	–0,78
Сред.	0,86	11,92	6,14	2,11	0,76	1,51	0,46	6,40	1,80	–0,59	–0,14	–0,75

Таблица 5. Невязка подбора, средний и максимальный модуль ошибки оценивания УЭС для каждой из моделей 1–9, %. Коэффициент корреляции между ошибками решения (со знаком) в слоях 1 и 2, 2 и 3, 3 и 4 (расчет на фактической сетке разносов)

Table 5. Fitting discrepancy, average and maximum modulus of error in resistivity estimation for each of the models 1–9, %. Correlation coefficient between solution errors (signed) in layers 1 and 2, 2 and 3, 3 and 4 (calculation on the actual spacing grid)

Модель	Невязка	R 1		R 2		R 3		R 4		Корреляция ошибок
		Макс.	Сред.	Макс.	Сред.	Макс.	Сред.	Макс.	Сред.	r 12	r 23	R 34
1	0,35	4,35	1,25	2,09	0,62	0,99	0,29	3,16	0,75	–0,31	0,21	–0,74
2	0,35	4,36	1,25	2,09	0,62	0,99	0,29	3,12	0,75	–0,31	0,21	–0,73
3	0,35	4,35	1,25	2,09	0,62	0,99	0,29	3,22	0,75	–0,31	0,21	–0,74
4	0,35	4,37	1,25	2,08	0,62	1,02	0,29	3,26	0,75	–0,31	0,21	–0,74
5	0,35	4,38	1,25	2,07	0,62	1,00	0,29	3,25	0,75	–0,31	0,21	–0,74
6	0,35	4,37	1,25	2,08	0,62	1,01	0,29	3,18	0,75	–0,31	0,21	–0,74
7	0,35	4,39	1,25	2,07	0,62	1,00	0,29	3,23	0,75	–0,31	0,21	–0,74
8	0,35	4,37	1,25	2,09	0,62	1,00	0,29	3,12	0,75	–0,31	0,21	–0,74
9	0,35	4,38	1,25	2,08	0,62	0,99	0,29	3,17	0,75	–0,31	0,21	–0,74
Сред.	0,35	4,37	1,25	2,08	0,62	1,00	0,29	3,19	0,75	–0,31	0,21	–0,74

Таблица 6. Отношение невязок подбора, среднего и максимального модуля ошибки оценивания УЭС для каждой из моделей 1–9 при расчетах на фактической и логарифмической сетках разносов Table 6. The ratio of the fitting residuals, the average and maximum modulus of error in resistivity estimation for each of models 1–9 when calculating on actual and logarithmic spacing grids

Модель	Невязка	Ошибка R 1		Ошибка R 2		Ошибка R 3		Ошибка R 4
		Макс.	Сред.	Макс.	Сред.	Макс.	Сред.	Макс.	Сред.
1	0,40	0,37	0,20	0,98	0,80	0,68	0,66	0,47	0,38
2	0,40	0,37	0,21	1,00	0,83	0,67	0,65	0,42	0,34
3	0,40	0,37	0,20	0,96	0,79	0,66	0,64	0,56	0,49
4	0,40	0,36	0,20	0,97	0,80	0,68	0,64	0,55	0,47
5	0,40	0,37	0,20	1,00	0,82	0,66	0,63	0,50	0,42
6	0,40	0,37	0,20	0,97	0,80	0,67	0,64	0,55	0,47
7	0,40	0,37	0,21	1,02	0,85	0,64	0,62	0,46	0,37
8	0,40	0,37	0,20	0,98	0,79	0,65	0,64	0,51	0,43
9	0,40	0,37	0,20	1,00	0,82	0,65	0,63	0,50	0,43
Сред.	0,40	0,37	0,20	0,99	0,81	0,66	0,64	0,50	0,42

При сравнении табл. 4 и 5 установлено, что переход к фактической сетке разносов позволяет резко уменьшить ошибки восстановления УЭС, однако величина эффекта отличается для разных слоев разреза. Отношение ошибок приведено в табл. 6. Наибольший эффект заметен в верхнем слое: после перехода на фактическую сетку (табл. 3) максимальная ошибка в слое 1 уменьшилась в 2,5 раза, а средняя по профилю – в 5 раз. Для второго слоя эффект значительно меньше: максимальная по профилю ошибка не изменилась, а средняя уменьшилась на 20 %. Сопротивление третьего слоя определяется наиболее точно; переход к фактической сетке разносов позволяет уменьшить ошибки примерно на треть. В нижнем четвертом слое разреза максимальная ошибка уменьшилась вдвое, а средняя по профилю – в 2,5 раза.

Ошибки для разных моделей почти одинаковы, что наиболее заметно при расчетах на фактической сетке разносов (табл. 5) и обусловлено тем, что наложенный на кривые кажущегося сопротивления фликкер-шум (формула 2) был одинаков для всех моделей М1–М9 (табл. 4). (Шум на разных линиях, разумеется, отличался.) Это было сделано для того, чтобы наиболее точно отследить эффекты, зависящие от модели. Одна из задач тестирования состояла в выборе наиболее адекватной модели сезонных эффектов для экспериментального разреза ( Бобачев и др., 2022б ); использование разных реализаций шума для разных моделей затруднило бы решение этой задачи.

Помимо уменьшения абсолютной величины ошибок (в относительных единицах), после перехода на фактическую сетку разносов значительно улучшилась структура ошибок. При решении обратной задачи на логарифмической сетке разносов высокоамплитудная раскачка наблюдается на границе слоев 1 и 2 (коэффициент корреляции ошибок –0,59, см. табл. 4). Аналогичные результаты были получены в работах ( Бобачев и др. , 2020а, 2020б ), где использовались немного отличающиеся синтетические профили. По-видимому, раскачка на границе слоев 1 и 2 возникает прежде всего из-за смещения сопротивления верхнего слоя, которое определяется не очень надежно, а интерполяция данных к логарифмической сетке разносов данный эффект (раскачку) усугубляет. В этой связи стоит заметить, что при использовании моделей с большим числом слоев эффект раскачки многократно усиливается, что было показано в работах ( Дещеревский и др., 2018б; Бобачев и др., 2020а ).

На границе слоев 2 и 3 эффект раскачки был умеренным при инверсии на логарифмической шкале (табл. 4) и исчез после перехода к фактической шкале разносов (табл. 5). Очевидно, это связано с хорошей проявленностью данных слоев сразу на нескольких разносах и достаточно малой ошибкой восстановления в них УЭС.

Вместе с тем раскачка на границе слоев 3 и 4 была очень высокой при расчетах на логарифмической сетке, и она практически не уменьшилась при переходе к фактической сетке разносов. Таким образом, эффект раскачки не обязательно связан с интерполяцией данных к логарифмической сетке разносов. Для борьбы с этим эффектом необходимо использовать регуляризацию алгоритма инверсии.

Сравнение результатов для экспериментального профиля

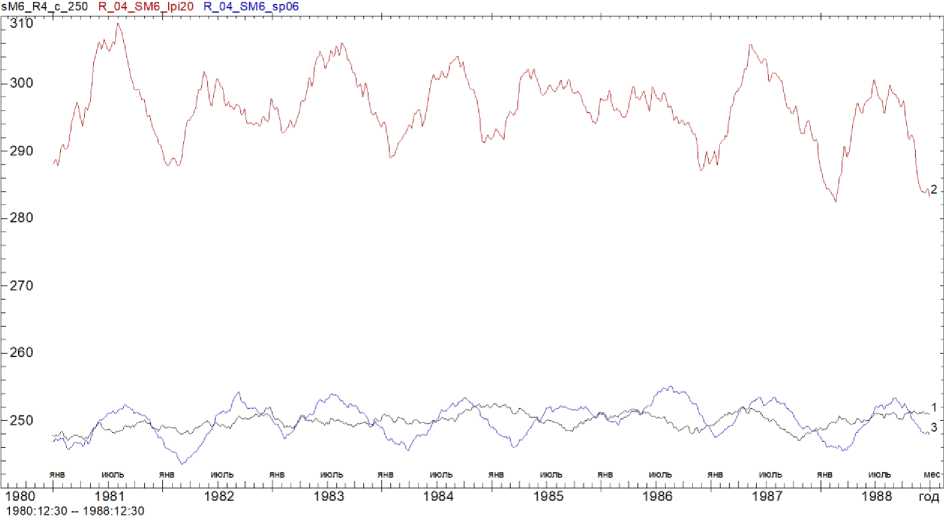
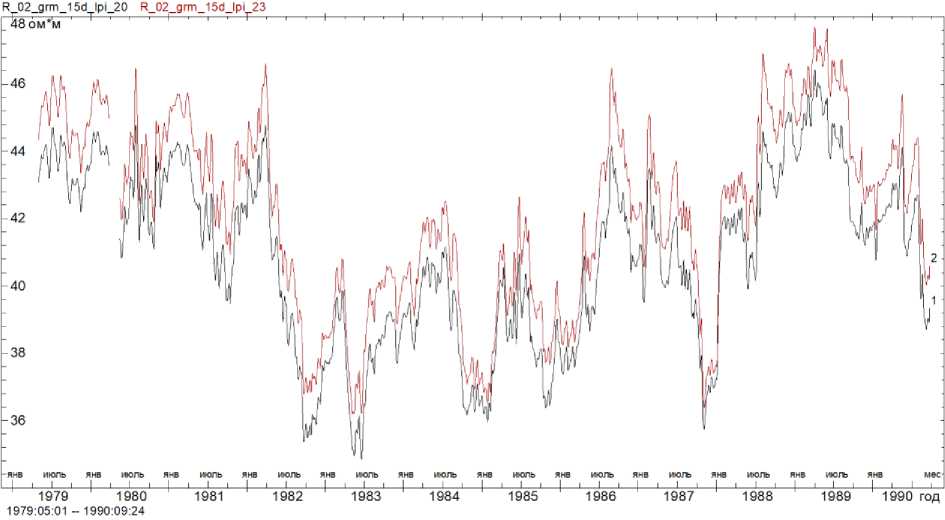
Сравнение рис. 2 и 3 показывает, что при обработке экспериментального профиля два варианта решения также характеризуются большим смещением кривых УЭС друг относительно друга. Выше при анализе синтетических данных было однозначно показано, что это смещение характерно именно для логарифмической сетки разносов (рис. 2). При расчетах на фактической сетке разносов величина смещения кратно меньше (кривые 1 и 3 лежат гораздо ближе друг к другу, чем кривые 1 и 2). С учетом этого, можно ожидать, что и для экспериментального профиля истинные значения УЭС гораздо более близки к тем значениям, которые рассчитаны в программе IPI_2023.

Оценки амплитуды смещения дают для слоев 1–4 значения, указанные в табл. 7. Как видно из таблицы, амплитуда смещения достаточно велика даже для слоев 2 и 3, УЭС которых, согласно результатам численных тестов, восстанавливается довольно надежно (табл. 4–6). В слоях 1 и 4 величина смещения достигает гигантских значений (10 и 20 %). И хотя при анализе временных вариаций постоянное смещение не является большой проблемой (так как основная цель мониторинга – контроль изменений УЭС), столь значительные погрешности говорят об очевидных проблемах с точностью инверсии при использовании логарифмической сетки разносов.

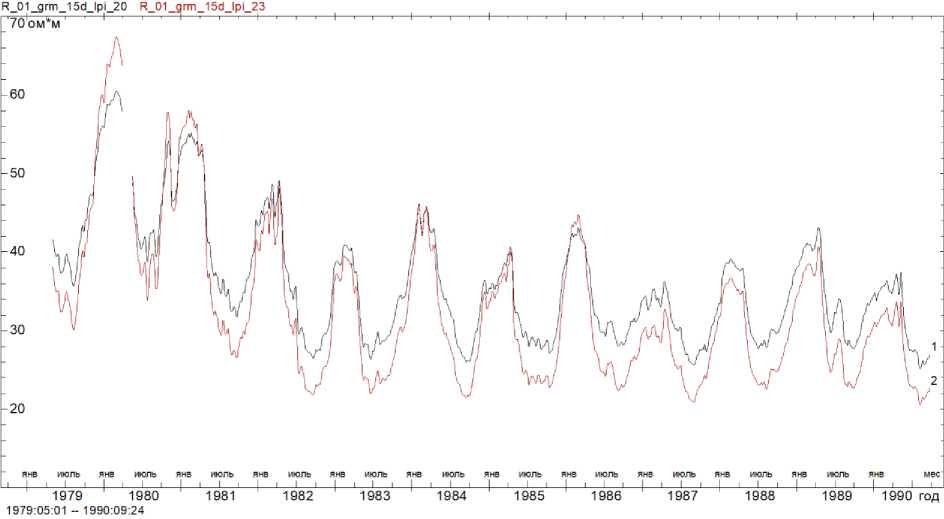
а

б

Рис. 3. Кривые УЭС для экспериментального профиля, сглаженного скользящим окном шириной 15 сут с гауссовым ядром ( Дещеревский и др. , 2016а, 2016б, 2016в ), рассчитанные в программах IPI_2020 (кривая 1) и IPI_2023 (кривая 2): а – слой 1; б – слой 2 Fig. 3. Resistance curves for an experimental profile smoothed by a sliding window 15 days wide with a Gaussian core ( Deshcherevskii et al. , 2016а, 2016б, 2016в ) calculated in programs IPI_2020 (curve 1) and IPI_2023 (curve 2): а – layer 1; б – layer

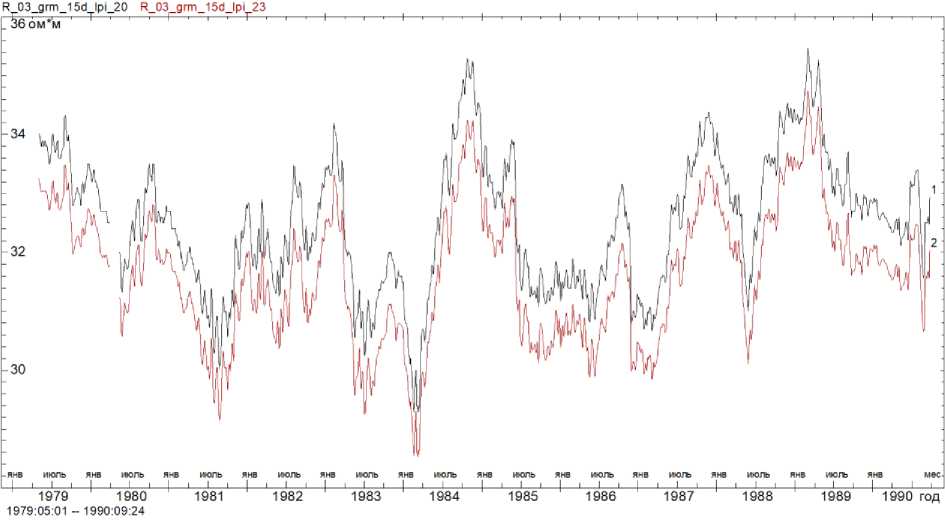
в

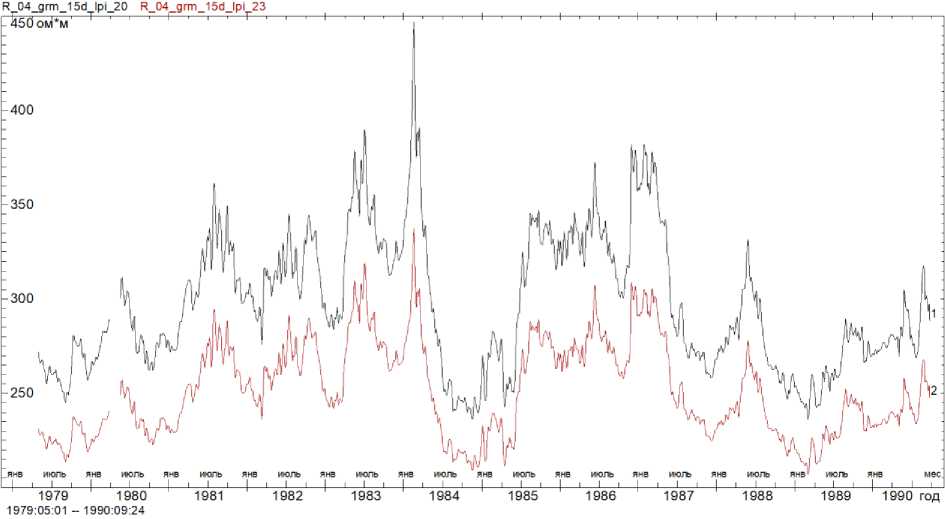
Рис. 3(продолжение). Кривые УЭС для экспериментального профиля, сглаженного скользящим окном шириной 15 сут с гауссовым ядром ( Дещеревский и др. , 2016а, 2016б, 2016в ), рассчитанные в программах IPI_2020 (кривая 1) и IPI_2023 (кривая 2): в – слой 3; г – слой 4 Fig. 3(continued). Resistance curves for an experimental profile smoothed by a sliding window 15 days wide with a Gaussian core ( Deshcherevskii et al. , 2016а, 2016б, 2016в ) calculated in programs IPI_2020 (curve 1) and IPI_2023 (curve 2):

в – layer 3; г – layer 4

Таблица 7. Смещение среднего значения УЭС при переходе на фактическую сетку разносов. Показана величина смещения при обработке профилей ВЭЗ, сглаженных 3- и 15-суточным скользящим окном с гауссовым ядром ( Дещеревский и др. , 2016а, 2016б, 2016в )

Table 7. Shift of the average resistivity value when switching to the actual spacing grid. The magnitude of the displacement when processing VES profiles smoothed by the 3- and 15-day sliding window with a Gaussian kernel is shown ( Deshcherevskii et al. , 2016а, 2016б, 2016в )

Слой	Смещение при сглаживании окном 3 сут, %	Смещение при сглаживании окном 15 сут, %
1	–9,83	–9,81
2	3,21	3,20
3	–2,76	–2,75
4	–18,28	–18,26

Из позитивных моментов можно отметить тот факт, что относительно короткопериодные вариации УЭС, рассчитанные двумя способами, достаточно хорошо согласуются между собой (рис. 3). Это свидетельствует о том, что ошибки восстановления изменений УЭС, вероятно, значительно меньше, чем ошибки восстановления среднемноголетних значений (приведенные в табл. 7 цифры можно рассматривать как верхнюю оценку этих ошибок). А учитывая, что разность между двумя решениями, согласно рис. 2 и табл. 4, 5, преимущественно обусловлена погрешностями решения в IPI_2020, можно предположить, что ошибки решения обратной задачи для экспериментального профиля в IPI_2023 должны быть кратно меньше, чем разница между двумя вариантами инверсии (в двух вариантах программы). Более детальное обсуждение величины этих ошибок выходит за рамки данной работы. [подробнее см. ( Бобачев и др., 2022б, 2022г )]. Следует отметить, что при использовании улучшенных алгоритмов инверсии, реализованных в программе IPI_2023, данные ошибки должны еще немного уменьшиться.

Анализ рис. 3 показывает наличие сильных противофазных вариаций УЭС в слоях 3 и 4. Согласно результатам, представленным в работах ( Бобачев и др., 2020а, 2022а, 2022б ), это может косвенно свидетельствовать о наличии эффекта раскачки сопротивлений (в отличие от тестов на синтетических данных, для экспериментального профиля прямая проверка наличия раскачки путем анализа ошибок решения невозможна). Обсуждение методов борьбы с этим эффектом не входит в задачи настоящей работы [см. ( Бобачев и др., 2020б, 2022а, 2022б, 2022в, 2022г )].

Заключение

Мониторинг геодинамических процессов с использованием электрометрических методов предполагает, что целевой физической характеристикой являются вариации удельного электрического сопротивления горных пород на различных глубинах. Однако на практике многие используемые методы, включая и метод вертикального электрического зондирования, непосредственно измеряют кажущееся сопротивление. В этом случае обязательным элементом интерпретации является переход от кажущихся сопротивлений к удельным. В частности, при использовании метода ВЭЗ с этой целью решается обратная задача ВЭЗ.

В конце XX в. авторами настоящей работы был проведен уникальный эксперимент по мониторингу вариаций сопротивления верхних слоев земной коры методом ВЭЗ в высокосейсмичном районе Памира с преобладанием мелкофокусных землетрясений. На полигоне функционировала плотная сеть стационарных сейсмических станций, которые окружали пункт зондирования со всех сторон, располагаясь на расстоянии от 15 до 50 км. Высочайший для своего времени методический уровень сейсмических наблюдений позволил оценивать координаты и особенно глубину гипоцентров землетрясений с недостижимой ранее точностью ( Лукк и др., 1973; Гармский…, 1990, Автоматизированная…, 1991; Попандопуло, 1991 ). В частности, было установлено, что за время эксперимента в непосредственной близости от зондируемого объема произошло несколько местных землетрясений, причем в двух случаях очаг непосредственно захватил зондируемый объем. Второй особенностью этого эксперимента было широкое комплексирование методов мониторинга ( Гармский…, 1990, Автоматизированная…, 1991 ), что резко расширяет возможности физической интерпретации результатов, полученных каждым методом, но и накладывает особые требования на точность выполняемых измерений.

Непрерывные (ежедневные) зондирования методом ВЭЗ продолжались более 10 лет. Для наблюдений использовалась специально разработанная аппаратура. Благодаря накоплению сигнала, точность измерений кажущегося сопротивления в полевых условиях достигала 0,01 % ( Осташевский и др., 1990, 1991; Сидорин и др., 1996 ). С учетом различных помех и шумов, реальная погрешность измерений была близка к 0,1 % ( Дещеревский и др., 2004, 2018а ). Предполагалось, что это позволит обнаружить изменения напряженно-деформированного состояния геосреды во время подготовки и реализации близких сильных землетрясений, а также исследовать процесс релаксации геосреды после сейсмического события ( Сидорин, 1986, 1992 ).

Однако анализ полученных данных ограничивался кажущимися сопротивлениями из-за непозволительно низкой точности доступных программ инверсии кривых ВЭЗ. Она вполне достаточна для решения геолого-структурных задач, но для эффективного мониторинга вариаций УЭС в нижних слоях разреза погрешность необходимо уменьшить примерно на два порядка ( Дещеревский и др., 1997а, 2004 ).

Авторами были предприняты значительные усилия для решения этой задачи. Был подобран оптимальный вариант геоэлектрического разреза для пункта зондирований, позволяющий наиболее точно отслеживать вариации УЭС с учетом сезонных эффектов, а в данных был устранен так называемый "геологический шум" ( Дещеревский и др., 2017, 2018а, 2018б ). Также была разработана прецизионная версия программы IPI, в которой учитывались специфические особенности измерительной установки. Тем не менее последующий анализ восстановленных в новой программе сезонных вариаций УЭС показал, что они не удовлетворяют критериям правдоподобности ( Дещеревский и др., 2018б; Бобачев и др., 2020а ).

Причины этого были установлены после проведения большой серии численных экспериментов на синтетических данных. Эксперименты подтвердили, что первоначальное решение действительно содержит значительные ошибки, возникающие из-за особого вида эквивалентности по сопротивлениям, – эффекта раскачки сопротивлений ( Бобачев и др., 2020а ).

По результатам тестирования в программу IPI был внесен ряд усовершенствований и улучшений, направленных как на регуляризацию обратной задачи ( Бобачев и др., 2020б, 2022а ), так и на оптимизацию других вычислительных процедур. В настоящей работе рассмотрен один из аспектов данной модернизации, связанный с внедрением расчетов на фактической (вместо логарифмической) сетке разносов. Анализ результатов инверсии синтетических профилей показал, что для рассматриваемого разреза (установки) это позволяет многократно уменьшить погрешность восстановления первого (верхнего) и также, что более важно, четвертого (нижнего) слоя разреза. Одновременно переход к расчетам на фактической сетке разносов полностью подавил раскачку сопротивлений на границе слоев 1 и 2, благодаря чему появилась возможность отказаться от использования регуляризирующей поправки к функционалу невязки на границе слоев 1 и 2 и уменьшить вес указанной поправки на границе слоев 3 и 4. Последнее обстоятельство является особенно важным, поскольку регуляризация не является "бесплатной" и приводит к смещению некоторых параметров восстановленного разреза ( Бобачев и др., 2022а, 2022б, 2022г ).

Недостаток расчетов на фактической сетке разносов заключается в определенном увеличении времени счета. Этот рост может стать довольно заметным при обработке многослойных профилей ВЭЗ, содержащих большое число пикетов, так как в процессе подбора прямую задачу приходится решать многократно на каждом пикете. Однако быстрый рост вычислительных мощностей в настоящее время позволяет во многих случаях снять это ограничение и делает нецелесообразным пересчет фактических данных на логарифмическую сетку разносов.

В целом полученные результаты показывают, что пересчет данных на логарифмическую шкалу разносов может приводить к существенному смещению параметров для некоторых разрезов. Ошибки могут возрастать в том случае, если разрез содержит один или несколько слоев небольшой мощности (либо это крайние слои разреза), которые имеют максимальную (по сравнению с другими слоями) проявленность лишь на одном разносе. В такой ситуации интерполяция данных к другому разносу может приводить не только к смещению параметров решения, но и к резкому росту раскачки сопротивлений. И наоборот, для тех слоев разреза, влияние которых доминирует сразу на нескольких разносах, пересчет сетки разносов вряд ли будет критичным.

Полученные в настоящей работе результаты вносят важный вклад в методические основы интерпретации данных прецизионных режимных ВЭЗ, в том числе выполненных на Гармском полигоне; их физической интерпретации будет посвящена отдельная публикация.

Работа выполнена в рамках государственного задания Института физики Земли им. О. Ю. Шмидта РАН.