Эффективная конечно-элементная модель для расчета индентирования сэндвич-панели
Автор: Абдрахимов Руслан Рамильевич, Долганина Наталья Юрьевна, Широков Александр Бежанович
Рубрика: Расчет и конструирование
Статья в выпуске: 4 т.15, 2015 года.
Бесплатный доступ
Разработана вычислительно-эффективная малопараметрическая конечно-элементная модель композитного материала для прогнозирования прочности и поглощенной энергии при низкоскоростном ударе. Объект исследования - трехслойная сэндвич-панель, представляющая собой два слоя хаотически армированного стеклопластика, между которыми расположен ячеистый заполнитель марки Divinycell ™P100. Механические характеристики стеклопластиковой обшивки для расчетной модели были определены из экспериментов на растяжение, изгиб и срез. В расчетах ячеистый заполнитель был представлен в виде сплошной нелинейной гиперупругой модели материала OgdenFoam (первого порядка), что позволило существенно сократить вычислительные затраты. Константы данной модели были определены из соответствующих кривых при одноосном и двухосном растяжении/сжатии, чистом сдвиге, а также трехосном растяжении/сжатии для оценки изменения объема. Поскольку проведение подобных экспериментов затруднительно, необходимые диаграммы деформирования были получены из расчета элементарной ячейки Кельвина (тетракаидодекаэдр), подходящей для описания регулярной структуры заполнителя. Ячейка Кельвина является повторяемой формой, заполняющей пространство без пустот при минимальном отношении площади поверхности к объему. Результаты расчетов локального деформирования трехслойной сэндвич-панели с использованием модели гиперупругого материала OgdenFoam вполне удовлетворительно отразили наблюдаемую в экспериментах нелинейность диаграмм (зону перелома) и показывают полную энергетическую эквивалентность вплоть до разрушения обшивки путем среза. Таким образом, разработанная конечно-элементная модель может быть использована для прогнозирования прочности и оценки предельной энергии низкоскоростного удара.
Сэндвич-панель, индентирование, гиперупругость, ячейка кельвина
Короткий адрес: https://sciup.org/147151703
IDR: 147151703 | УДК: 539.422.5 | DOI: 10.14529/engin150403
Текст научной статьи Эффективная конечно-элементная модель для расчета индентирования сэндвич-панели
Ведение. Трехслойные панели (сэндвич-панели) широко используются в аэрокосмической индустрии и транспортном машиностроении благодаря тому, что среди несущих оболочечных элементов они обладают одним из лучших сочетаний удельной прочности, жёсткости, простоты изготовления и ремонта [1–2].
Наряду с преимуществами у сэндвич-панелей имеются и недостатки: чувствительность к низкоскоростному ударному нагружению, которому они нередко подвергаются в процессе эксплуатации. Повреждения, полученные в результате низкоскоростного удара, могут существенно снизить остаточную жесткость и прочность панели [3].
Наиболее подробно в литературе представлены конструкции с сотовым заполнителем из алюминия или изотропного пластика [4–9]. В последнее время все большее внимание уделяется пористым заполнителям с замкнутыми ячейками (пенам) [10–15]. Также проводятся исследования заполнителей, формируемых при помощи элементов цилиндрической формы, например, волокон с ориентацией, близкой к трансверсальной [16–18]. Возросший интерес к пенозаполните-лям объясняется тем, что помимо обеспечения требуемых механических характеристик они позволяют придать панели свойства тепло- и звукоизоляции.
В качестве обшивок рассматриваются слоистые пакеты из однонаправленных стекло- и углепластиков [4, 7, 11], и тканевые пакеты [5, 6, 8–10, 12, 13]. Больший интерес к тканевым материалам вызван их лучшей сбалансированностью по механическим характеристикам в слое и повышенной межслойной прочностью [13].
Методы расчета низкоскоростного удара можно разделить на две группы: аналитические и конечно-элементные (КЭ). Аналитические модели в большинстве случаев применимы для расче- та упругой работы сэндвич-панели и перестают быть адекватными после возникновения пластических деформаций или повреждений.
Конечно-элементные методы расчета [4, 7–9, 12, 13, 19] являются более точны м и, имеют возможность учета всех наблюдаемых механизмов накопления повреждений и разруш е ния материалов панелей.
На сегодняшний день не существует общеприн я тых математических моделей композитных материалов, используемых в конечно–элементных расчетах на низкоскоростной удар сэндвич-панелей. Разработанные исследователями модели требуют значительного объема пре д варительных испытаний, необходимых для идентификации параметров, верификации алгоритмов расчета накопления повреждений и деградации механически х свойств материала при ударе, а т акже требовательны к производительности компьютеров.
Таким образом, конечно-элементные методы расчета являются перспек т ивным направлением в области оценки прочности сэндвич-панелей при н изкоскоростном ударе, однако высокая вычислительная трудоемкость затрудняет их применение при инженерном пр о ектировании.
Целью данной работы является разработка эффективной малопара м етрической конечноэлементной модели для расчёта локального индентирования сэндвич-пане л и с учетом особенностей используемых материалов.
Экспериментальная часть. Объектом исследования является трехслойная сэндвич-панель (рис. 1), состоящая из двух слоев хаотически-армированного стеклопластика (ХАСП), между которыми расположен ячеистый заполнитель марки DivinycellP100. Заполнитель разделен на элементы размерами 29 ×29 ×40 мм, с незаполненными зазорами шириной 1 мм между ними, благодаря чему возможно использование данного материала для размещения н а поверхностях, обладающих кривизной. Образцы сэндвич-панелей были изготовлены на базе НОЦ «Ко м позитные материалы и конструкции» ФГБОУ ВПО «ЮУрГУ».

Рис. 1. Схема испытания сэндвич-панели с заполнителем, имеющим зазоры
Испытания на индентирование проведены на универсальной испытательной машине INSTRON 5882. В поверхность сэндвич-панели вдавливали цилиндрические инденторы, диаметром 23 и 16 мм, со скоростью 5 мм/мин. Разрушение сэндвич-панели происходило путем среза стеклопластиковой обшивки (рис. 2), которому предшествовали сжатие заполнителя.
Для определения механических свойств стеклопластиковой обшивки для расчетной модели сэндвич-панели были проведены испытания на растяжение, изгиб и срез.
Модуль упругости определен из испытания на изгиб по ГОСТ 25.604–82, на 5 образцах.
Предел прочности и коэффициент Пуассона о п ределены из испытаний на растяжение по ГОСТ 25.601–80, на 5 образцах.
В результате проведённых испытаний свойства стеклопластиковой обшивки в плоскости (плоскости изотропии) равны: коэффициент Пуассона μ = 0,25; модуль упругости Е = 11,2 ГПа; предел прочности на растяжение σ Т = 195 ± 10 МПа. Трансверсальные константы упругости слабо влияют на локальную жесткость сэндвич-панелей, поэтому в данной работе не исследовались. Из трансверсальных характеристик прочности в данном случае важнейшей является прочность на срез. Испытания на срез проведены на пяти образцах исследуемого стеклопластика размерами 50 × 50 × 3 мм с использованием опоры в виде кольца внутренним диаметром 16 мм и нагружающим элементом в виде втулки с наружным диаметром 15 мм. Полученное разрушающее напряжение среза равно 42 ± 4 МПа. Это значение ниже используется для определения предельной расчётной нагрузки при локальном деформировании сэндвич-панелей.
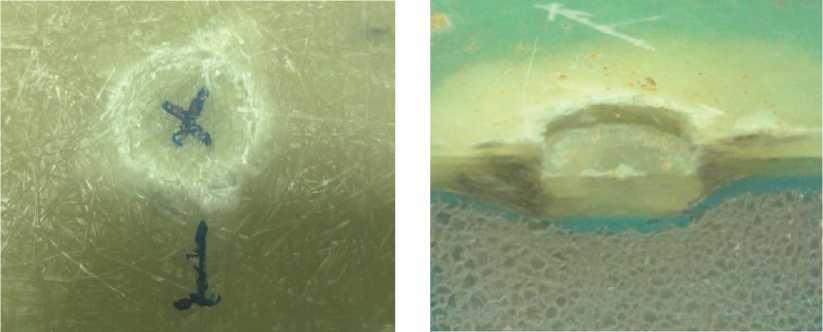
Рис. 2. Разрушение обшивки сэндвич-панели
Заполнитель Divincell P100 во время испытаний на сжатие показал пластичность, объемную сжимаемость, которые можно описать при однократном нагружении моделью гиперупругого материала с участками упругости, «размягчения» и упрочнения, для расчета которых в КЭ пакетах применяются известные модели Муни-Ривлина, Огдена и др. Параметры таких моделей определяются при помощи кривых деформирования пеноматериалов при одноосном и двухосном рас-тяжении/сжатии, сдвиге и трехосном сжатии для оценки изменения объема, которые сложно получить экспериментальным путем, в связи с чем они будут определены расчетным путем ниже.
Расчетная часть. Геометрически модель локального деформирования представляет собой трехслойную сэндвич-панель, изображенную на рис. 1, с учетом особенностей макроструктуры заполнителя и наличия в нем незаполненных зазоров шириной 1 мм. Механические характеристики материала стеклопластиковой обшивки, используемые в расчете, были определены ранее из испытаний на растяжение, изгиб и срез.
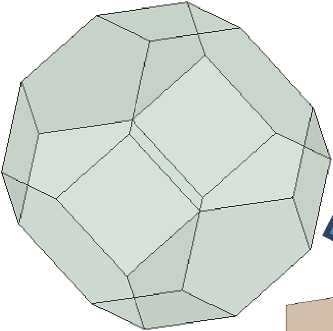
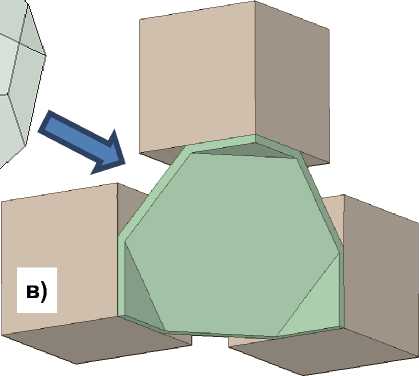
Диаграммы деформирования заполнителя (для вычисления констант гиперупругой модели) были определены из расчета элементарной ячейки микроструктуры при одно-, двух- и трехосных испытаниях. В качестве расчетной трехмерной модели микроструктуры была выбрана форма Кельвина [20] (тетракаидодекаэдр, рис. 3, б) с постоянной толщиной стенок. Важно отметить, что пены с малой пористостью имеют сферические поры, а с увеличением кратности (или коэффициента снижения плотности) форма пор стремится к тетракаидодекаэдру. Данная форма отвечает двум критериям: пространство заполняется повторяемой формой без зазоров и соотношение площади поверхности ячейки к объему минимально (это важно с точки зрения термодинамических соображений).
Параметры ячейки (средний диаметр и толщина) определены при помощи анализа микрофотографий поверхности заполнителя (рис. 3, а), который имеет структуру, состоящую из закрытых тонкостенных ячеек. Средний диаметр ячейки равен 0,953 мм, толщина стенки равна 20,2 мкм (определена из условия соответствия экспериментально измеренной плотности заполнителя ρ з = 110 кг/м 3 и известной плотности исходного материала – полиэтилентерефталата, ρ п = 1400 кг/м 3 ).

Рис. 3. Моделирование ячеистой структуры заполнителя: а – поверхность заполнителя DivinycellP100; б – ячейка Кельвина; в – расчётная модель ячейки
б)
в)
Для данной ячейки методом КЭ проведены расчеты случаев одноосного и двухосного растя-жения/сжатия, чистого сдвига и трехосного растя ж ения/сжатия. Материал ячейки – полиэти-лентерефталат, заданный в виде упругопластического материала: модуль упругости Е = 3 ГПа, коэффициент Пуассона µ = 0,4, предел текучести σ т = 55 МПа [21]. Для упрощения расчета, ввиду симметричности формы, была использована 1/8 часть ячейки (рис. 3, в), выполненной объемными элементами типа Solid (два элемента по толщи н е). На трех плоских гранях ячейки располагались вспомогательные жесткие кубические элементы, с контактом типа NoSeparation. Этот тип контакта обеспечивает одинаковость нормальных перемещений во всех точках контактной поверхности и отсутствие ограничений на перемещения в плоскости контакта. На отсеченных гранях расчетной модели были заданы условия зеркальн о й симметрии.
Были проведены расчеты деформирования модели для случаев одноосного и двух о сного рас-тяжения/сжатия, чистого сдвига и трехосного растя ж ения/сжатия для оценки изменен и я объема. Нагружение модели было кинематическим с автом а тическим определением реакций опор для последующего вычисления осредненных напряжени й (рис. 4).
Расчетные диаграммы деформирования были использованы для определения пара м етров модели гиперупругого материала Ogdenfoam (первого порядка): ^ = 0,917 МПа; a t = 43,2; P i = 0 (см. рис. 4).
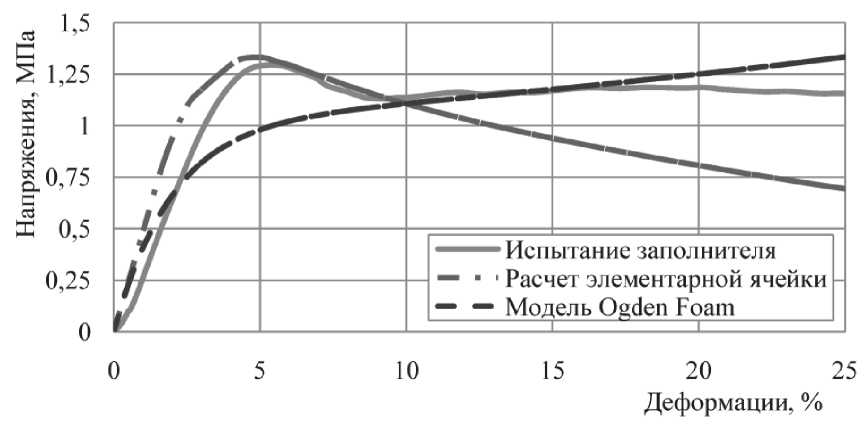
Рис. 4. Диаграммы деформирования при одноосном сжатии
Результаты расчета сэндвич-панели с использованием данной модели заполнител я представлены на рис. 5, 6 (серым цветом обозначена область разброса экспериментальных данных; осред-ненная диаграмма «нагрузка – перемещение» – п р ерывистой линией; результаты расчета – сплошной линией). В расчете контакт между сэндвич-панелью и индентором был задан в виде
Frictional (коэффициент трения 0,2), нагружение кинематическое, с опред е лением реакций на инденторе.
В качестве критерия остановки расчетов деформирования сэндвич-панели использовалось достижение напряжениями среза стеклопластиковой обшивки величины 4 2 МПа, полученной выше экспериментально.
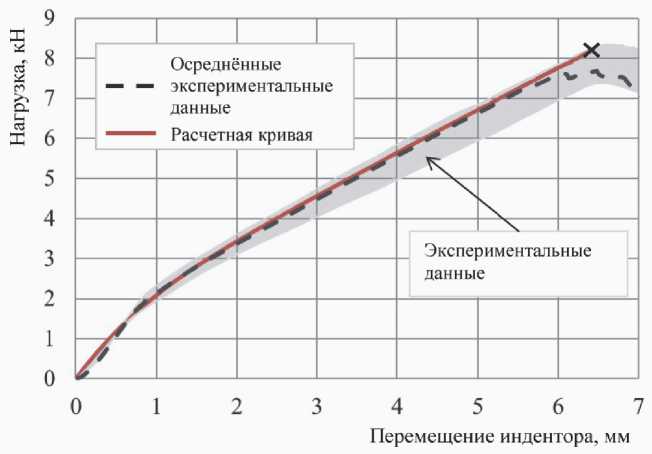
Рис. 5. Диаграмма «нагрузка – перемещение» при индентировании сэндвич-панели индентором, диаметром 23 мм
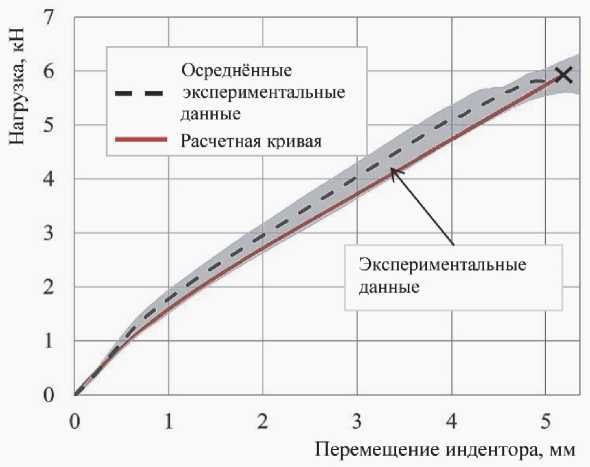
Рис. 6. Диаграмма «нагрузка – перемещение» при индентировании сэндвич-панели индентором, диаметром 16 мм
Следует отметить, что модель гиперупругого мат е риала типа OgdenFoa m вполне удовлетворительно отразила наблюдаемую в экспериментах нелинейность диаграмм контактного деформирования (зону перелома) и обеспечила полную энергетическую эквивалентность вплоть до разрушения обшивки путем среза.
Заключение. Разработана эффективная малопараметрическая конечно-элементная модель трехслойной сэндвич-панели, служащая для прогнозирования прочности и оценки предельной энергии низкоскоростного удара. Необходимые механические свойства обшивки панели были определены экспериментальным путем, а свойства ячеистого заполнителя – из расчета упрощенного представления структуры заполнителя в виде ячейки Кельвина. Полученные диаграммы деформирования ячейки были использованы для определения констант гиперупругой модели первого порядка типа OgdenFoam. Разработанная расчетная модель трехслойной сэндвич-панели показывает удовлетворительное соответствие с полученными экспериментально кривыми локального деформирования и может быть использована при оценке предельной энергии низкоскоростного удара по сэндвич-конструкциям транспортных средств.
Работа выполнялась при финансовой поддержке Минобрнауки РФ в рамках проекта «Создание высокотехнологичного производства модельного ряда инновационных энергосберегающих трамвайных вагонов модульной конструкции для развития городских пассажирских транспортных систем» по договору № 02.G25.31.0108 от 14.08.2014 г.
Список литературы Эффективная конечно-элементная модель для расчета индентирования сэндвич-панели
- Zenkert D. The Handbook of Sandwich Construction. 2nd Ed. EMAS Press, 1997. 442 р.
- Расчет трехслойных конструкций: справ./под ред. В.Н. Кобелева. М.: Машиностроение, 1984. 300 с.
- Abrate S. Impact on Composite Structures. Cambridge, Cambridge University Press, 1998. 290 p. DOI: DOI: 10.1017/CBO9780511574504
- Meo M., Morris A.J., Vignjevic R., Marengo G. Numerical Simulations of Low-Velocity Impact on an Aircraft Sandwich Panel. Composite Structures, 2003, vol. 62, p. 353-360. DOI: DOI: 10.1016/j.compstruct.2003.09.035
- Fatt M.S.H., Park K.S. Dynamic Model for Low-Velocity Impact Damage of Composite Panel. Part A: Deformation. Composite Structures, 2001, vol. 52, p. 335-351. DOI: DOI: 10.1016/S0263-8223(01)00026-5
- Fatt M.S.H., Park K.S. Dynamic Model for low-Velocity Impact Damage of Composite Panel. Part B: Damage Initation. Composite Structures, 2001, vol. 52, p. 353-364. DOI: DOI: 10.1016/S0263-8223(01)00045-9
- Shengqing Z., Boay C.G. Damage and Failure Mode Maps of Composite Sandwich Panel Subjected to Quasi-Static Indentation and Low Velocity Impact. Composite Structures, 2013, vol. 101, p. 204-214. DOI: DOI: 10.1016/j.compstruct.2013.02.010
- Ivañez I., Sanchez-Saez S. Numerical Modelling of the Low-Velocity Impact Response of Composite Sandwich Beams with Honeycomb Core. Composite Structures, 2013, vol. 106, p. 716-723. DOI: DOI: 10.1016/j.compstruct.2013.07.025
- Ivañez I., Barbero E., Sanchez-Saez S. Analytical Study of the Low-Velocity Impact Response of Composite Sandwich Beams. Composite Structures, 2014, vol. 111, p. 459-467. DOI: DOI: 10.1016/j.compstruct.2014.01.028
- Shin K.B., Lee J.Y., Cho S.H. An Experimental Study of Low-Velocity Impact Responses of Sandwich Panels for Korean Low Floor Bus. Composite Structures, 2008, vol. 84, p. 228-240. DOI: DOI: 10.1016/j.compstruct.2007.08.002
- Feng D., Aymerich F. Damage Prediction in Composite Sandwich Panels Subjected to Low-Velocity Impact. Composites. Part A, 2013, vol. 52, p. 12-22. DOI: DOI: 10.1016/j.compositesa.2013.04.010
- Zhou J., Hassan M.Z., Guan Z., Wesley J., Cantwell J. The Low Velocity Impact Response of Foam-Based Sandwich Panels. Composites Science and Technology, 2012, vol. 72, p. 1781-1790. DOI: DOI: 10.1016/j.compscitech.2012.07.006
- Wang J., Waas A.M., Wang H. Experimental and Numerical Study on the Low-Velocity Impact Behavior of Foam-Core Sandwich Panels. Composite Structures, 2013, vol. 96, p. 298-311. DOI: DOI: 10.1016/j.compstruct.2012.09.002
- Rajaneesh A., Sridhar I., Rajendran S. Relative Performance of Metal and Polymeric Foam Sandwich Plates under Low Velocity Impact. International Journal of Impact Engineering, 2014, vol. 65, p. 126-136. DOI: DOI: 10.1016/j.ijimpeng.2013.11.012
- Schubel P.M., Luo J.-J., Daniel I.M. Low Velocity Impact Behavior of Composite Sandwich Panels. Composites. Part A, 2005, vol. 36, p. 1389-1396. DOI: DOI: 10.1016/j.compositesa.2004.11.014
- Zhou D.W., Stronge W.J. Low Velocity Impact Denting of HSSA Lightweight Sandwich Panel. International Journal of Mechanical Sciences, 2006, vol. 48, p. 1031-1045. DOI: DOI: 10.1016/j.ijmecsci.2006.05.011
- Zhang G., Wang B., Ma L., Xiong J., Yang J., Wu L. The Residual Compressive Strength of Impact-Damaged Sandwich Structures with Pyramidal Truss Cores. Composite Structures, 2013, vol. 105, p. 188-198. DOI: DOI: 10.1016/j.compstruct.2013.05.016
- Hosur M.V., Abdullah M., Jeelani S. Manufacturing and Low-Velocity Impact Characterization of Foam Filled 3-D Integrated Core Sandwich Composites with Hybrid Face Sheets. Composite Structures, 2005, vol. 69, p. 167-181. DOI: DOI: 10.1016/j.compstruct.2004.06.008
- Klaus M., Reimerdes H.-G., Gupta N.K. Experimental and Numerical Investigations of Residual Strength after Impact of Sandwich Panels. International Journal of Impact Engineering, 2012, vol. 44, p. 50-58. DOI: DOI: 10.1016/j.ijimpeng.2012.01.001
- Thomson W. (Lord Kelvin) On the Division of Space with Minimum Partitional Area. Philosophical Magazine, 1887, vol. 24, iss. 151, p. 503-514. DOI: DOI: 10.1080/14786448708628135
- Калинчев Э.Л., Саковцева М.Б. Свойства и переработка термопластов: справ. пособие. Л.: Химия, 1983. 288 с.


