Эффективное управление взаимодействием членов спортивного коллектива с использованием идей искусственного интеллекта

Введение. Управление взаимодействием членов спортивного коллектива во время соревнования является главным условием для выигрыша команды, а следовательно, основным компонентом в комплексной системе подготовки высококлассных спортивных команд в игровых видах спорта. Решение этой задачи предполагает изучение истоков и механизмов формирования внутригрупповых, коллективных феноменов (чувств, установок, традиций и т. п.), а также разработку педагогических методов управления с целью создания благоприятного климата в спортивных командах и выявление социально-психоло- гических мотивов поведения и деятельности самих спортсменов [10, 16, 18].

Члены спортивного коллектива (команды) по-разному воспринимают реальную действительность, а иногда совсем неадекватно отвечают на реакции, например, на рекомендации тренера, находясь под влиянием разного рода зависимостей (эмоциональной неустойчивости, неуверенности в себе, повышенной склонности к риску, агрессивности, сензитивности, физической переутомляемо-сти, неприязни товарища по команде и т. п.) [2, 13, 16]. В условиях постоянной смены спортивной информации, большого количест- ва обрабатываемых данных (факторов и причин) руководителю коллектива очень сложно принимать верные решения. Задача правильного выбора альтернатив в таких условиях, как правило, должна сводиться к сужению их исходного множества с учетом их значимости, и тогда лицо принимающее решение (ЛПР – тренер, менеджер) получает наивысшую ожидаемую ценность своего выбора [11, 15, 18].

Под принятием спортивного решения понимается процесс выбора оптимальных альтернатив в спортивной практике с целью достижения наилучшего обучающего, воспитательного или управляющего спортивного результата (эффекта).

В работах российских ученых рассматривались вопросы теории принятия управленческих решений [9, 11]; вопросам выбора альтернатив посвятили свои научные труды зарубежные авторы Шину С. Аенгара [17] и Марк Р. Леппер [20]. Наибольший пласт научных работ посвящен психологическим особенностям принятия управленческих решений [3, 9, 18, 19] в спортивных коллективах, хотя сама проблема «механизма» выбора альтернатив все еще недостаточно изучена как в теоретическом, так и в практическом аспектах. Без внимания исследователей остались такие важные вопросы, как использование эффективных математических методов в принятии управленческих решений, основанных на идеях искусственного интеллекта.

Научное обоснование. Современный этап развития теории принятия управленческих спортивных решений чаще всего связан с неопределенностью психологической составляющей ЛПР. Дело в том, что у тренера, принимающего ответственное решение, идет борьба между самооценкой и самоконтролем. Неадекватная самооценка проявляется в противоборстве между двумя основными тенденциями: повышением уровня притязаний (то есть он, как и все здравомыслящие люди, желает иметь максимальный успех) и снижением уровня притязаний (тренер старается избежать неудачи). Психологический фактор ответственности вступает в «игру», а точнее в борьбу с желанием наибольшей эффективности (победы), при условии непредсказуемости результата выбора управленческого решения, особенно тогда, когда на кону стоят очень большие ставки (финал соревнований на крупном (престижном) международном турнире, спартакиаде, чемпионате, олимпиаде) [3]. Но при этом часто недооцениваются чисто прагматические способы и конструктивные методики в принятии эффективных управленческих спортивных решений [7, 14, 16]. Тем более когда они основаны на серьезной математической базе – использовании компьютерных систем искусственного интеллекта.

Отсылаем читателя к нашим работам в области практического использования интеллектуальных систем в вопросах принятия дидактических решений [4, 5] и уделим основное внимание лишь теоретической реализации методики принятия управленческих решений на основе алгоритмов искусственного интеллекта. Покажем «механизм» нахождения эффективного взаимодействия членов спортивного коллектива. Для примера возьмем волейбольную команду, состоящую из 6 человек. Тренер ставит определенную задачу этому спортивному коллективу, но при этом предполагает, что какие-то части могут выполняться отдельно каждым игроком, а в целом решается единая коллективная проблема. В зависимости от того, как игроки взаимодействуют друг с другом, зависит их общий результат всей игры.

Предположим, что предварительно был проведен педагогический эксперимент и было выяснено, как игроки работают (взаимодействуют) в парах, то есть друг с другом по два человека (рис. 1, см. таблицу).

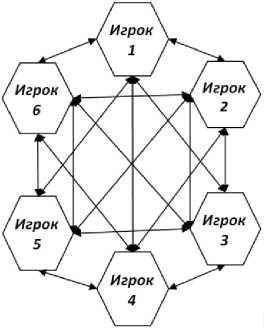
Рис. 1. Взаимодействие игроков в волейбольной команде

Fig. 1. Interaction of players in a volleyball team

Для нахождения подобных результатов эксперимента (коэффициентов взаимосвязи игроков) отсылаем читателя к многочисленным работам по психолого-педагогическим и индивидуально-спортивным измерениям, например [1, 6, 12, 21].

Из таблицы видно, что если поставить в паре первого игрока со вторым, то их общая игровая эффективность будет равна 2, а если первого с четвертым, которые между собой не ладят (например, они совместно долго не тренировались или вообще не подходят друг другу по каким-то иным параметрам: рост, вес, уровень мастерства, психологическая несовместимость и т. д.), то их общая эффективность будет равна –4.

Результаты предварительного педагогического эксперимента по взаимодействию игроков волейбольной команды Results of pre-pedagogical experiment on the interaction of volleyball team players

Игрок Player	1	2	3	4	5	б
1	0	2	-1	-4	5	1
2	2	0	6	3	-1	0
3	-1	6	0	1	0	-1
4	-4	3	1	О	4	-4
5	5	-1	0	4	0	-2
6	1	0	-1	-4	-2	0

Мы знаем, как игроки работают в парах, но наша задача состоит в том, чтобы определить, какова их общая (командная) наилучшая продуктивность. Для этого существует несколько способов, простейший из которых – это перебор всех вариантов, например, выясним коэффициент взаимодействия трех игроков: F{(4, 5, 6)} = 4 - 4 - 2 = -2.

Первое значение (4) берется из таблицы как взаимодействие четвертого игрока с пятым, второе (–4) – как взаимодействие четвертого с шестым, а третье (–2) – пятого игрока с шестым. Вместе получается, что эффективность такого варианта равна –2. Или другие варианты: F{(1,4, б)} = —4 + 1 — 4 = -7; F{(2, 3,4)} = 6 + 3 + 1 = 10.

А каким образом, зная такую матрицу эффективности попарного взаимодействия волейболистов, можно найти наилучшую пару игроков?

Для решения можно пойти самым простым путем – перебрать все варианты. Таких вариантов будет 26 – 1 = 63. Решить эту задачу можно вручную, но для этого понадобится некоторое время. Но если в команде большое число игроков, например в футболе их 11, тогда число вариантов перебора возрастает до 211 – 1 = 2047. При этом мы учли лишь взаимодействия игроков одной команды, но в реальной спортивной практике тренер обязан учесть и взаимосвязи с «привязанными» («приставленными») игроками команды соперника. Так, для той же футбольной команды максимальное число вариантов перебора становится равным 222 – 1 = 4194303. Вручную выполнить такие вычисления уже невозможно. Здесь на помощь должен прийти компьютер.

Практические рекомендации по осмыслению. В реальной спортивной практике игроки ведут себя не всегда правильно (идеально), и в этом прелесть и зрелищность настоящего спорта. Поэтому алгоритм решения таких задач необходимо искать в природных алгоритмах, они ведь тоже сродни алгоритмам поведения человека в спортивной ситуации. Ведь все живые существа совершают ошибки.

Воспользуемся « генетическим алгоритмом », который широко применяется в системах искусственного интеллекта и который является одним из ведущих методологических оснований для реализации в компьютерных интеллектуальных системах. Впервые мысли о его реализации были высказаны Чарльзом Робертом Дарвином относительно процессов эволюции в виде двух основополагающих положений: 1) во время рождения новых поколений происходят мутации, то есть изменения в геноме животного; 2) продолжают род те существа, которые наиболее приспособлены к окружающей среде.

Теперь снова рассмотрим ту же задачу о волейболистах, но уже с биологической точки зрения эволюции Ч. Дарвина. Предположим, что точное решение нам не требуется, а необходимо найти более или менее приемлемое ( хорошее ) решение.

Любой группе из шести игроков-волейболистов сопоставим некий код длиною 6 символов (у волейболистов 6 человек в команде). Код состоит из 0 и 1 (вспомните X и Y хромосомы в биологии): 0 – элемент не входит в группу; 1 – элемент входит в группу. Например, группа (1, 3, 6) = 101001. Почему такой код? А потому, что единица есть в этой группе,

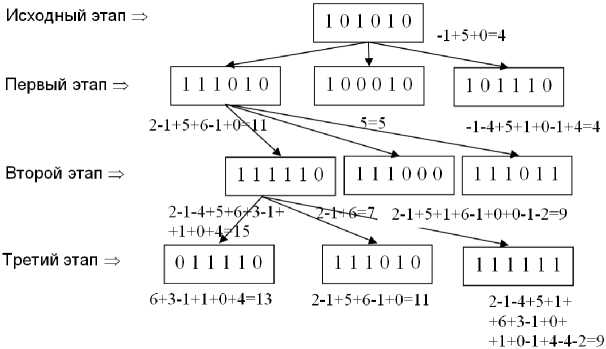
Рис. 2. Три этапа мутаций генного кода популяций

Fig. 2. Three stages of the mutations of a populations’ genetic code

поэтому выставляем код 1, двойки (точнее второго элемента) – в ней нет (ставим код 0), тройка в группе есть – поэтому ставим код 1, четверки в группе нет – ставим код 0, пятерки в группе снова нет – ставим код 0 и шестерка в группе есть – ставим код 1. Для ясности приведем коды еще двух других групп: (2, 4, 5) = 010110 и (2, 3, 5, 6) = 011011. Понятно, что каждой группе можно сопоставить некий код, и наоборот, каждому коду можно сопоставить некую группу. Это взаимно однозначное соответствие.

Этот код – это и есть генный код (биологи называют его геном) некоторого живого существа (популяции). Теперь нашу задачу переформулируем с точки зрения биологии: «Если каждому коду соответствует некая группа, то каждой группе соответствует некая эффективность: F{(101001)} = F{(1,3,6)} = = -1 + 1 - 1 = -1».

Такая эффективность будет выполняться настолько, насколько живое существо приспосабливается к окружающей среде. Чем выше код, тем лучше оно живет в окружающем мире. Найдем такой код.

Будем действовать так, как это происходит в самой природе. Пусть у нас есть некая исходная популяция, у которой код равен 101010. Для нее посчитаем эффективность существования (см. таблицу): F{(101010)} = = F{(1,3,5)} = -1 + 5+ 0 = 4.

Предположим, что у этой популяции возникла мутация, и при этом возникло три новых популяции. Напомним, что мутация – это случайное изменение кода с 0 на 1 (и наоборот). Например, поменяем вторую позицию (это 0), третью (1) и четвертую позицию

(тоже 0) на противоположное. Затем для каждой новой популяции посчитаем эффективность (рис. 2, первый этап).

Из рис. 2 видно, что для третьей мутации получилось самое большое число – 11. Оно больше, чем у исходной популяции (см. рис. 2, исходный этап). Именно эта ветвь эволюции на первом этапе является лучшей. Как раз по ней и пойдет развитие.

Теперь уже от нее (от первой мутации) на первом этапе, назовем ее первой популяцией, получаем новое разветвление (три новые мутации) второго этапа. Получается, что для этого периода развития первая (левая) мутация – самая лучшая, ее эффективность равна 15. Именно от этой популяции и пойдет следующее развитие.

Наконец, получим от нее третий этап трех мутаций.

Посчитаем эффективность вновь полученных популяций, они соответственно равны: 13, 11 и 9. Если сравнить их результаты с предыдущим (вторым) этапом, то можно сделать заключение, что все они имеют меньшее значение (13, 11, 9 < 15), следовательно, наилучшее решение было получено на втором этапе мутации генного кода живого существа. Дальше нет необходимости продолжать вычисления. Оптимальный (то есть наилучший в данных условиях) – это геном с кодом 111110, при котором для данных табличных значений наиболее подходящим будет вариант, когда стабильно хорошо взаимодействуют игроки: 1-й со 2-м, 1-й с 3-м, 1-й с 4-м, 1-й с 5-м, также 2-й с 3-м, 2-й с 4-м, 2-й с 5-м, а также 3-й с 4-м, 3-й с 5-м, и наконец, 4-й с 5-м игроком. Из этого видно, что игрок под номером 6 вообще не вписывается в коллективную игру команды.

Напомним, что такой алгоритм решения наверняка дал нам не самое идеальное (наилучшее) решение эффективности, но все же оно более-менее хорошее. Назовем его оптимальным с учетом небольшого числа переборов вариантов.

Результаты и обсуждение. Именно такие алгоритмы искусственного интеллекта и используются в поиске эффективных вариантов взаимодействия членов спортивного коллектива. Понятно, что они реализуются в виде программного кода в компьютерных интеллектуальных системах. В качестве примера можно привести программу STATІSTІCA Neural Networks (производитель StatSoft).

Заключение. Используя интеллектуальные системы, можно достаточно точно и объективно выполнять расчеты в управлении игроками спортивной команды, без ошибок принимать как промежуточные, так и окончательные решения по взаимодействию не только членов своего спортивного коллектива, но и игроков команды соперника, что в итоге приводит к высоким спортивным результатам. Таким способом тренер (преподаватель физкультуры) гарантированно может прогнозировать результаты спортивных достижений в игровых видах спорта. Управление взаимодействием игроков команды является просчитанной гарантией победы в соревнованиях (турнирах). Модель, основанная на компьютерной системе искусственного интеллекта, дает возможность тренеру и спортивному менеджеру продуктивно управлять индивидуальными особенностями разноплановых игроков команды. Это позволяет избежать субъективизма не только на стадии тренировок, но и на этапе ответственных выступлений. Интеграция спортивных и информационных технологий является велением времени и сейчас невозможно провести четкой грани, с одной стороны, между достижениями в сфере спортивного менеджмента, и с другой – между успехами в области математики и компьютерных технологий в принятии эффективных управленческих спортивных решений.