Эффективность устранения аварий в системе ЖКХ в условиях неопределенности

Конечной целью функционирования системы жизнеобеспечения является бесперебойное и постоянное воссоздание естественной среды обитания человека, куда можно отнести, во-первых, поддержание биоэнергетического потенциала за счет производства предметов потребления и продуктов питания, создания комфортных условий труда, транспортного обеспечения и т.п., и, во-вторых, обеспечение в жилых и производственных помещениях холодного, горячего водоснабжения, водоотведения, отопления, вентиляции и освещения, что, в свою очередь производит и поставляет сектор коммунальной энергетики. При этом функционирование всех ее составляющих звеньев, относится к группе элементов локальной монополии, в отличие от объектов большой энергетики, объектов Газпрома и Российских железных дорог, относящихся к естественной монополии. Таким образом коммунальная энергетика оперирует энергоносителями некоторого среднего потенциала, а именно [4]: температуры энергоносителей составляют 350 градусов по Цельсию, давление – порядка 3 мегапаскалей, а мощность, например, электроснабжения достигает 35 киловатт.

Благодаря отрицательным тенденциям, сложившимся в последнее время в области коммунальной энергетики, развивается производственная безответственность и снижение общего качества работы всей системы в целом, при этом возникают так называемые «веерные» отключения от энергоснабжения целых микрорайонов, что серьезно вредит всем сторонам этой системы. Еще одна беда всего жилищнокоммунального хозяйства (ЖКХ) – это очень большая изношенность производственного фонда. Согласно официальной статистике 2012 г. более 70% основных фондов ЖКХ выработали свой ресурс.

Аварии в коммунальных системах жизнеобеспечения в основном происходят в городах и крупных населенных пунктах, причем помимо материальных потерь они наносят серьезный моральный ущерб населению. Можно выделить четыре группы аварий:

• -    на канализационных системах;

• -    на тепловых сетях;

• -    в системах водоснабжения;

• -    на коммунальных газопроводах.

При проектировании специализированной базы аварийно-спасательной службы ЖКХ требуется определить численность и состав аварийно-спасательных бригад для ликвидаций последствий возникающих аварий в системах жизнеобеспечения. Подобная проблема требует принятия оптимального решения в условиях неопределенности.

Условиями неопределённости считается ситуация, когда результаты принимаемых решений неизвестны. Различают два основных вида неопределённостей: [2] стохастическая (вероятностная) – когда имеется информация о распределении вероятности на множестве результатов и априорная – когда отсутствует информация о возможных результатах, либо когда события происходят от случая к случаю, и в то же время они никакую статистическую устойчивость не обнаруживают. Задача обоснования решений в условиях стохастической неопределённости, за исключением априорной, сводится к выбору из исходного множества альтернатив – элементов решения Х какого-то элемента х.

Обоснование же решений в условиях априорной неопределённости при явном недостатке информации для линейных непрерывных систем основывается на методе Ляпунова, методе гиперустойчивости или градиентном методе с использованием функций чувствительности; для объектов с нелинейными параметрами используются методы [3] скоростного градиента, методы теории бинарных систем, методы теории систем с разрывным управлением или итеративными процедурами синтеза, что выходит за рамки Настоящей статьи.

Для определения наиболее предпочтительного варианта решения проблемы поддержания безаварийного функционирования коммунальной системы жизнеобеспечения, предположим, в части холодного и горячего водоснабжения, в условиях стохастической неопределенности вводится некий единственный критерий эффективности W , исходя из требуемого целеполагания.

В общем случае показатель эффективности W , как случайная величина, будет определяться как:

W = W ( a , e , x ) , (1)

где: а – некоторая совокупность заданных, заранее известных факторов; е – некоторая совокупность неизвестных (случайных) факторов; х – конкретный выбранный элемент решения.

Необходимо отметить, что добиться создания строго детерминированной задачи можно было бы лишь в исключительных случаях, когда влияние случайного фактора е не существенно, т.е. отклонения неких параметров от их среднего значения незначительны, и его значение можно было бы заменить его математическим ожиданием (МО). Однако в нашем случае фактор е является существенно случайным.

Можно воспользоваться так называемым приемом – оптимизацией в среднем, рассматривая в качестве показателя эффективности на саму случайную величину W , а ее МО – , которое можно было бы максимизировать или минимизировать. Разумеется, что и при таком подходе неопределенность сохраняется, поскольку в процессе ликвидации аварий могут возникнуть непредвиденные ситуации и в самой аварийно-спасательной базе, предназначенной для этих целей.

Тогда можно ввести некоторое стохастическое ограничение [1], например, время ожидания вызова ремонтной бригады W будет меньше некоторого значения W 0 . Таким образом можно из всего множества Х необходимо изъять все элементы х с вероятностью, скажем, меньше 0,99.

На практике при оценке эффективности устранения аварий в системах коммунального жизнеобеспечения приходится иметь дело со случайными процессами, которые могут характеризоваться дискретными состояниями. Подобные процессы удобно рассматривать, используя схему, называемую графом состояний, а при помощи стрелок указывать возможные переходы между ними.

Рассмотрим гипотетический пример из двух объектов (систем горячего и холодного водоснабжения), которые могут находиться в двух дискретных состояниях: система работоспособна – «1» и система в состоянии выхода из строя – «0». На рисунке 1 приводится размеченный граф состояний систем горячего и холодного водоснабжения. Рассматриваемая система имеет 4 состояния:

• S 1    – >  работают 2 системы (холодного и горячего водоснабжения);

• S 2    – >  работает система холодного водоснабжения, система горячего водоснабжения ремонтируется;

• S 3    – >  работает система горячего водоснабжения, система холодного водоснабжения ремонтируется;

• S 4    – >  ремонтируются 2 системы (холодного и горячего водоснабжения).

Переходы S 1 – > S 2 , S 1 – > S 3 , S 2 – > S 4 , S 3 – > S 4 совершаются в результате происходящих аварийных отказов, как системы холодного, так и горячего водоснабжения, которые по существу представляют собой поток однородных событий, которые следуют друг за другом. Причем, как только в системе появляется событие, так сразу же совершается переход из одного состояния в другое. Обратные переходы являются следствием ремонтных работ. Отказы в системах холодного и горячего водоснабжения происходят в непредсказуемые моменты времени. Случайны также моменты времени, соответствующие окончанию ремонтов. Очевидно, что и переходы объектов из одного состояния в другое, также являются случайными процессами. Заметим, что на рисунке 1 не показаны переходы S 1 – > S 4 и S 4 – > S 1, поскольку первый переход отвечает одновременному отказу обоих устройств, а второй – одновременному окончанию ремонта обоих устройств, т.к. можно предположить, что вероятности таких совпадений = 0.

Исходя из того предположения, что вероятность перехода Si – > Sj в некоторый выбранный промежуток времени от t до t + ∆ t должна равняться вероятности появления события в потоке в этот же промежуток времени. Эту вероятность можно обозначить через Р ij ( t, ∆ t ). В пределе при ∆ t –> 0 переходим к плотности вероятности перехода в момент t :

Pi ( t , A t )

Lj(t ) = lim A t ^ 0 ^jAT" ’ ⁽²⁾

которая также называется интенсивностью потока событий, зависящая в общем случае от времени.

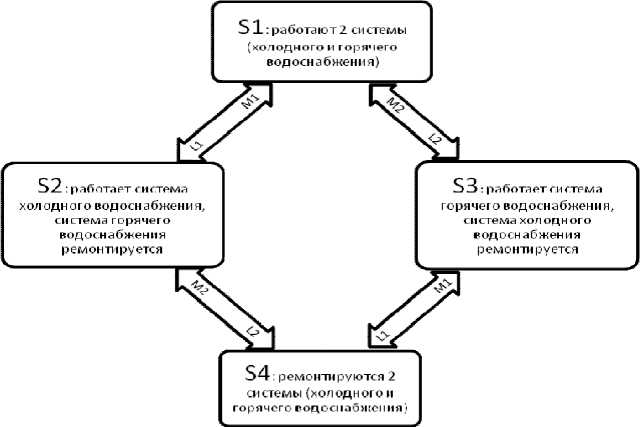
Рисунок 1. Размеченный граф состояний систем горячего и холодного водоснабжения

В дальнейшем для оценки эффективности устранения аварий в нашем примере коммунальной системы жизнеобеспечения целесообразно использовать уравнение Колмогорова для стационарного режима [5], когда вероятности не зависят от времени. С этой целью вводятся следующие обозначения, а именно: L 1 – интенсивность потока отказов системы горячего водоснабжения; L 2 – интенсивность потока отказов системы холодного водоснабжения;

M 1 – интенсивность окончания ремонтов системы горячего водоснабжения; M 2 – интенсивность окончания ремонтов системы холодного водоснабжения.

Пусть имеется N >>  1 систем коммунального жизнеобеспечения, подобных описываемой с помощью размеченного графа состояний, изображенного на рисунке 1. Число систем, находящихся в состоянии Si , равно Np i . Из состояния S 1 возможны переходы в состояние S 2 и S 3 с суммарной вероятностью L 1 + L 2, отнесенной к единице времени. Тогда число уходов из состояния S 1 в единицу времени в рассматриваемой коллекции систем равно Np i (L 1 + L 2 ). Приходы в состояние S 1 совершаются из S 2 и S 3, а их число в единицу времени равно Np 2 M 1 + Np 3 M 2. Поскольку рассматривается стационарный режим, то число уходов и приходов для каждого состояния должны быть сбалансированы. Следовательно,

Np i (L 1 + L 2 ) = Np ₂ M 1 + Np 3 M 2 . (3)

Рассматривая баланс уходов и приходов для каждого из четырех состояний и сокращая в уравнениях общий множитель N, получаем следующие уравнения относительно вероятностей р 1 , р 2 , р 3 , р 4 :

• -для состояния S 1:

( L1 + L 2) p ₁ = M 1 p ₂ + M 2 p 3 ; (4.1)

для состояния S 2:

( L 2 + M1 ) p ₂ = L 1 p 1 + M 2 p ₄; (4.2)

для состояния S 3:

• ( L 1 + M 2) p ₃ = L 2 p 1 + M 1 p ₄;   (4.3)

для состояния S 4:

• ( M 1 + M 2) p ₄ = L 2 p ₂ + L1 p ₃ .  (4.4)

Нетрудно убедиться, что уравнение (4.4) может быть получено сложением уравнений (4.1) + (4.2) + (4.3). Вместо уравнения (4.1) воспользуемся уравнением (5):

• p 1 + p 2 + p 3 + p 4 = ¹ ,         ⁽⁵⁾

которое означает, что выбранная в качестве примера коммунальная система жизнеобеспечения с вероятностью = 1 (т.е. достоверно) находится в каком-либо из 4-х состояний Si .

В таком случае размеченный граф состояний, приведенный на рисунке 1, может быть представлен в виде системы уравнений Колмогорова, а именно:

• ( L 1 + L 2) p 1 = M 1 p ₂ + M 2 p ₃ ;

• ( L 2 + M 1) p ₂ = L 1 p 1 + M 2 p 4 ;

• ( L 1 + M 2) p ₃ = L 2 p 1 + M 1 p 4 ;

• p 1 ⁺ p 2 ⁺ p 3 ⁺ p 4 = ^1.

Для оценки эффективности устранения аварий в рассматриваемой коммунальной системе жизнеобеспечения (КСЖ) предположим, что состав аварийно-спасательной бригады, осуществляющей ремонт системы холодного водоснабжения (АСБ-2) оснащена более совершенным оборудованием и имеет производительность вдвое большую, нежели аварийно-

^    (6)

спасательная бригада, осуществляющая ремонт системы горячего водоснабжения – АСБ-1. Предполагается, что круглосуточная бесперебойная подача горячей воды потребителю в течение одного календарного месяца приносит КСЖ прибыль а 1 = 50 тысяч рублей, а круглосуточная бесперебойная подача холодной воды приносит прибыль а 2 = 100 тысяч рублей. Штрафные санкции е , предположим, начисляются только в случае одновременного ремонта обеих систем водоснабжения в зависимости от времени недопоставки обоих видов водоснабжения. В рассматриваемом случае отказы системы холодного водоснабжения происходят в среднем вдвое чаще, чем системы горячего водоснабжения, т.е. L 11 = 1, а L 12 = 2. Интенсивность потока окончания ремонтов принимается: М 11 = 2, а М 12 = 3. Используя заданные интенсивности потоков отказов и потоков окончания ремонтов, переписываются уравнения (6) в виде:

• 3 P i = 2 p 2 + 3 p 3 ;

• ⁴ P 2 = P i ^{+ 3} P 4 ;

• ⁴ P 3 = ² P i ^{+ 2} P 4 ;

P i ⁺ P 2 ⁺ P 3 ⁺ P 4 = i

Решением этой системы уравнений являются следующие значения вероятностей: р 1 = 0,4; р 2 = 0,2; р 3 = 0,27; р 4 = 0,13. Это означает, что в среднем 40 % времени обе системы холодного и горячего водоснабжения работают одновременно (состояние S 1 на рисунке 1), 20 % времени работает только система горячего водоснабжения, а система холодного водоснабжения в это время ремонтируется (состояние S 2), 27 % времени работает только система холодного водоснабжения, а система горячего водоснабжения ремонтируется (состояние S 3), 13 % времени обе системы водоснабжения одновременно находятся в состоянии ремонта (состояние S 4).

Экономический эффект, приносящий от функционирования АСБ-1 и АСБ-2 в течение одного календарного месяца составляют: а 1 =а 11 +а 12 = (50+100)^.0,4+ 50^.0,2+ 100^.0,27 =97,0 тысяч рублей.

Штрафные санкции в этом случае составляют: е 1 =150^.0,13= 19,5 тысяч рублей.

В итоге эффективность W 1 составит: W 1 = а 1 - е 1 =77,5 тысяч рублей.

Теперь предположим, что интенсивность потока окончания ремонтов для системы холодного водоснабжения увеличилась вдвое, т.е. М21 =4, а остальные интенсивности остаются прежними: М22 =3, L21 = 1, а L22 = 2. В таком случае система уравнений (6) принимает следующий вид:

• ³ P i = ⁴ P 2 ^{+ 3} P 3 ;

• ⁶ P 2 = P i ^{+ 3} P 4 ;

• ⁴ P 3 = ² P i ^{+ 4} P 4 ;

  
  

P i ⁺ P 2 ⁺ P 3 ⁺ P 4 = ⁱJ

Решением этой системы уравнений (8) являются следующие значения вероятностей:

р 1 = 0,48; р 2 = 0,12; р 3 = 0,32; р 4 = 0,08.

Тогда с учетом полученных вероятностей АСБ-1 и АСБ-2 приносит следующую прибыль в течение одного календарного месяца: а2=а21+а22 =(50+100) .0,48+ 50.0,12+ 100.0,32 =110,0 тысяч рублей.

Штрафные санкции в этом случае составляют: е 2=150^.0,08 = 12,0 тысяч рублей. В итоге эффективность W 2 составит: W 2 = а 2 -е 2=98,0 тысяч рублей.

Таким образом, при увеличении интенсивности потока окончания ремонтов, эффективность процесса устранения увеличивается.

Выводы: случайные процессы в системах с дискретным состоянием, в качестве которых можно выбрать системы жизнеобеспечения, осуществляющие бесперебойное и постоянное воссоздание естественной среды обитания человека, могут быть рассмотрены с помощью размеченных графов состояний. Количественная оценка поведения этих систем при выборе требуемых параметров в условиях неопределенности достаточно просто описывается и решается с помощью уравнения Колмогорова для стационарного режима, что и показано при сравнении двух выполненных гипотетических расчетах.