Эффективные численные методы решения задачи PageRank для дважды разреженных матриц

в разных вариантах: минимизация квадратичной формы || Ах — 6 || 2 и минимизация бесконечной нормы || Ах — 6 || ^ на единичном симплексе. Здесь А = Р ^т — I, I — единичная матрица. К аналогичным задачам приводят задачи анализа данных (Ridge regression, LASSO [7]), задачи восстановления матрицы корреспонденций по замерам трафика на линках в компьютерных сетях [8] и многие другие задачи. Особенностью постановок этих задач, так же как и в случае задачи PageRank, являются колоссальные размеры.

В данной статье планируется сосредоточиться на изучении роли разреженности матрицы А, на использовании рандомизированных подходов и на специфике множества, на котором происходит оптимизация. Симплекс является (в некотором смысле) наилучшим возможным множеством, которое может порождать (независимо от разреженности матрицы А) разреженность решения (см., например, п. 3.3 С. Бубек, 2014 [9], это тесно связано с l1-оптимизацией [10]).

Все, о чем здесь написано, хорошо известно на таком уровне грубости. Детально поясним, в чем заключаются отличия развиваемых в статье подходов от известных подходов. Прежде всего мы вводим специальный класс дважды разреженных матриц (одновременно разреженных и по строкам и по столбцам). ¹ Такие матрицы, например, возникают в методе конечных элементов и в более общем контексте при изучении разностных схем. ² Если считать, что матрица А имеет размеры п х п, а число элементов в каждой строке и столбце не больше чем s ^ п, то число ненулевых элементов в матрице может быть sn. Кажется, что это произведение точно должно возникать в оценках общей сложности (числа арифметических операций типа умножения или сложения двух чисел типа double) решения задачи (с определенной фиксированной точностью). Оказывается, что для первой постановки (минимизация квадратичной формы на симплексе) сложность может быть сделана пропорциональна s ² ln(2 + п/s ² ) (разделы 2 и 3), а для второй (минимизация бесконечной нормы) и того меньше — s lnn (раздел 4).

Первая задача может решаться обычным прямым градиентным методом с 1-нормой в прямом пространстве [11], [12] — нетривиальным тут является в том числе организация работы с памятью. В частности, требуется хранение градиента в массиве, обновление элементов которого и вычисления максимального/минимального элемента должно осуществляться за время, не зависящие от размера массива (то есть от п). Тут оказываются полезными фибоначчиевы и бродалевские кучи [13]. Основная идея — не рассчитывать на каждом шаге градиент функции заново А^т Ах к +1 , а пересчитывать его, учитывая, что х к +1 = х к + е к , где вектор е к состоит в основном из нулей:

А^тАх _{к +1} = А^тАх _к + А^тАе _к .

Детали будут изложены в разделе 2. Аналогичную оценку общей сложности планируется получить методом условного градиента Франка–Вульфа [14], большой интерес к которому появился в последние несколько лет в основном в связи с задачами BigData (М. Ягги [15], Аршуи–Юдицкий–Немировский [16], Ю.Е. Нестеров [17]). Аккуратный анализ работы этого метода также при правильной организации работы с памятью позволяет (аналогично предыдущему подходу) находить такой х, что || Ах — Ь || 2 6 Е за число арифметических операций

О

( п +

s ² ln(2 + п/s ² )

Е2

'

причем оценка оказывается вполне практической. Этому будет посвящен раздел 3.

Вторая задача (минимизации || Ах — 6 || ^ на единичном симплексе) с помощью техники Юдицкого–Немировского, 2012 (см. п. 6.5.2.3 [18]) может быть переписана как седловая задача на произведение двух симплексов. Если применять рандомизированный метод зеркального спуска (основная идея которого заключается в вычислении вместо градиента Ах стохастического градиента, рассчитываемого по следующему правилу: с вероятностью х і он равен первому столбцу матрицы А, с вероятностью Х 2 - второму и т.д.), то для того, чтобы обеспечить с вероятностью >  1 — ст неравенство || Ах — 6 || ^ 6 Е достаточно выполнить

О(п 1п( п/ст ) /е ² )

арифметических операций. К сожалению, этот подход не позволяет в полном объеме учесть разреженность матрицы А. В статье предлагается другой путь, восходящий к работе Григориадиса–Хачияна, 1995 [19] (см. также [20]). В основе этого подхода лежит рандомизация не при вычислении градиента, а при последующем проектировании (согласно XL-расстоянию, что отвечает экспоненциальному взвешиванию) градиента на симплекс. Предлагается вместо честной проекции на симплекс случайно выбирать одну из вершин симплекса (разреженный объект!) так, чтобы математическое ожидание проекции равнялось бы настоящей проекции [20]. В работе планируется показать, что это можно эффективно делать, используя специальные двоичные деревья пересчета компонент градиента [6]. В результате планируется получить следующую оценку для дважды разреженных матриц:

О(п + s Inn 1п( п/ст ) /е ² ) .

Напомним, что при этом число ненулевых элементов в матрице А может быть sn. Возникает много вопросов относительно того, насколько все это практично. К сожалению, на данный момент наши теоретические оценки говорят о том, что константа в О() может иметь порядок 10 2 . Подробнее об этом будет написано в разделе 4.

В данной статье при специальных предположениях относительно матрицы PageRank Р (дважды разреженная) мы предлагаем методы, которые работают по наилучшим известным сейчас оценкам для задачи PageRank в условиях отсутствия контроля спектральной щели матрицы PageRank [6]. А именно, полученная в статье оценка (см. разделы 2, 3)

О ^п +

s ² 1п(2 + n/s ² )

Е2

)

сложности поиска такого х, что || Ах — Ь || 2 6 Е, является на данный момент наилучшей при s ^ ^п для данного класса задач. Быстрее может работать только метод MCMC (для матрицы с одинаковыми по строкам внедиагональными элементами)

О (1п п 1п(п/ст) / ( ое ² ))

требующий, чтобы спектральная щель а была достаточно большой [6].

Приведенные в статье подходы применимы не только к квадратным матрицам А и не только к задаче PageRank. В частности, можно обобщать приведенные в статье подходы на композитные постановки [21]. Тем не менее свойство двойной разреженности матрицы А является существенным. Если это свойство не выполняется и имеет место, скажем, только разреженность в среднем по столбцам, то приведенные в статье подходы могут быть доминируемы рандомизированными покомпонентными спусками. Если матрица А сильно вытянута по числу строк (такого рода постановки характерны для задач анализа данных), то покомпонентные методы применяются к двойственной задаче [22], [23], если по числу столбцов (такого рода постановки характерны для задач поиска равновесных конфигураций в больших транспортных/компьютерных сетях), то покомпонентные методы применяются к прямой задаче [24], [25]. Подчеркнем, что при условии двойной разреженности А с s ^ ^п нам неизвестны более эффективные (чем приведенные в данной статье) способы решения описанных задач. В частности, это относится и к упомянутым выше покомпонентным спускам.

В заключительном пятом разделе работы приводятся результаты численных экспериментов.

• 2.    Прямой градиентный метод в 1-норме

Задача поиска вектора PageRank может быть сведена к следующей задаче выпуклой оптимизации [12] (далее для определенности будем полагать 7 = 1, в действительности, по этому параметру требуется прогонка)

1Ъ

/^{( х )} = У^{| Ах||} 2 + ⁷ ^2(- ж ^г ) + ^ min .

^{2         2} ~ =1         vM=1

где А = Р ^Т — I , I — единичная матрица, е = (1,..., 1) ^Т ,

₌ / 1. V >  ⁰

^{( V ) +}     10, V < 0

При этом мы считаем, что в каждом столбце и каждой строке матрицы Р не более s ^ ^п элементов отлично от нуля (Р — разрежена). Эту задачу предлагается решать обычным градиентным методом, но не в евклидовой норме, а в 1-норме (см., например, [11]):

х к +1 = х к + arg min ^ : ( ^,е ) =0

{

/ (х к ) + (V / (х к ).Һ )

+ L || Һ || 1 },

где L = max ||А^||2 + 1 6 3 ( А^ — г-й столбец матрицы А). Точку старта хо итераци-і=1,...,п онного процесса выберем в одной из вершин симплекса.

Для достижения точности е ² по функции потребуется сделать

O(LR²/e² ) = О(1/е²)

итераций [11]. Не сложно проверить, что пересчет градиента на каждой итерации заключается в умножении АТАҺ, что может быть сделано за O(s2). Связано это с тем, что вектор Һ всегда имеет только две компоненты max д/ (хк )/дхі — min д/(хк )/дхі) и — ( max д/(хк )/дхі — min д/ (хк )/дхі)

8 \ і=1,...,п                      і=1,...,п                  )         8 \ і=1,...,п                      і=1,...,п                  у отличные от нуля (такая разреженность получилась благодаря выбору 1-нормы), причем эти компоненты определяются соответственно как arg min д/ (хк )/дхі и arg max д/(хк )/дхг. і=1,...,п                        і=1,...,п

Это можно пересчитывать (при использовании кучи для поддержания максимальной и минимальной компоненты градиента) за О (s2 ln(2 + п/s2)). Указанная оценка достигается следующим образом: группа из п координат разбивается на s2 +1 непересекающихся групп по не более чем п/s2 в каждой. Операция обновления компоненты градиента осуществляется в соответствующей ей группе (за время О (ln(2 + п/s2)) с помощью бинарной кучи [13]). Выбор минимальной компоненты градиента осуществляется просмотром не более чем s2 +1 вершин кучи (в вершине кучи расположен минимальный элемент). Аналогичным образом поддерживается набор куч с максимальным элементом в корне для поиска максимальной компоненты градиента. Важно отметить, что логарифмический фактор указанного вида не улучшаем. Последнее следует из неулучшаемости оценки скорости сортировки О(п 1пп), основанной на попарном сравнении элементов. Таким образом, с учетом препроцессинга и стоимости первой итерации О(п) общая трудоемкость предложенного метода будет

О Qi +

s ² 1n(2 + n/s ² )

Е2

'

что заметно лучше многих известных методов [6].

Некоторая проблема состоит в том, что в решении могут быть маленькие отрицательные компоненты, и требуется прогонка по 7. Также для того, чтобы сполна использовать разреженность, требуется либо «структура разреженности» (скажем, заранее известно, что матрица А имеет отличные от нуля элементы только в s/2 окрестности диагонали), либо препроцессинг. В нашем случае (впрочем, это относится и к последующим разделам) препроцессинг заключается в представлении матрицы по строкам в виде списка смежности: в каждой строке отличный от нуля элемент хранит ссылку на следующий отличный от нуля элемент, аналогичное представление матрицы делается и по столбцам. Заметим, что препроцессинг помогает ускорять решения задач не только в связи с более полным учетом разреженности постановки, но и, например, в связи с более эффективной организацией рандомизации [6].

Обратим внимание на то, что число элементов в матрице Р , отличных от нуля, даже при наложенном условии разреженности (по строкам и столбцам) все равно может быть достаточно большим sn. Удивляет то, что в оценке общей трудоемкости этот размер фактически никак не присутствует. Это в перспективе (при правильной организации работы с памятью) позволяет решать задачи колоссальных размеров. Более того, даже в случае небольшого числа не разреженных ограничений вида

( a, ж ) = b i , г = 1, ...,т = О(1)

можно «раздуть» пространство (не более чем в два раза), в котором происходит оптимизация (во многих методах, которые учитывают разреженность, это число входит подобно рассмотренному примеру, так что такое раздутие не приведет к серьезным затратам), и переписать эту систему в виде Аж = b, где матрица будет иметь размеры О(п) х О(п), но число отличных от нуля элементов в каждой строке и столбце будет О(1). Таким образом, допускается небольшое число «плотных» ограничений.

В заключение заметим, что после переформулировки исходной задачи мы ушли от оптимизации на симплексе и стали оптимизировать на гиперплоскости, содержащей симплекс. Проблема тут возникает из-за того, что нужно оценить l1-размер множества Лебега функции J (ж) для уровня J (ж о ), где ж о € 5 _П (1) — точка старта (см. [11]), 5 „ (1) — единичный симплекс в R ” . Можно показать, что это приводит к уже использованной нами выше оценке R = О(1). Но, к сожалению, точного значения R мы не знаем. Как следствие, при практической реализации метода мы не можем просто сделать предписанное число итераций и остановиться. Однако выход есть. В данной задаче мы знаем оптимальное значение: J * = 0. Сделав N = 1 /е ² итераций, можно за О(sn) арифметических операций проверить, выполняется ли условие J (ж ү ) 6 Е ² /2 или нет. Если нет, то N = 3N, и продолжаем итерационный процесс (брать ли число 3 или какое-то другое > 1, можно определить исходя из того, как соотносятся sn и s ² /e ² , чем больше второе первого, тем меньше надо брать это число). Минус тут в том, что тогда оценка получится

О (т + п2 + s), а не

О („ +    ■         •■) , как хотелось бы. С другой стороны, избавляться совсем от sn в данном случае и не обязательно, поскольку в следующем разделе предлагается метод, где этих проблем нет.

• 3.    Метод условного градиента Франка–Вульфа

Перепишем задачу поиска вектора PageRank следующим образом

/^{( х )} = 1 ^||Ах|| 2 ■ min 2             xgs „ (1)

Для решения этой задачи будем использовать метод условного градиента Франка–Вульфа [14] – [17]. Напомним, в чем состоит метод.

Выберем одну из вершин симплекса и возьмем точку старта Х 1 в этой вершине. Далее по индукции, шаг которой имеет следующий вид. Решаем задачу

(V/(хк то/   ■ min yes„(i)

Обозначим решение этой задачи через

У к = (0,..., 0,1, 0,..., 0), где 1 стоит на позиции

і к = arg min д/ (ж к )/дх ^г . г =1 ,...,п

Положим

Х к +1 = (1 - 7 к )х к + 7 к У к , 7 к = ГГГ, к = 1, 2,... к + 1

Имеет место следующая оценка [14] – [17]

/ (X N ) = / ( xn ) - / * 6

2L _P R ² N + 1 ,

где

R 2 6   max || у — х || 2 , Ly 6 max (h, A^TAh') = max || Ah || 2 , 1 6 p 6 to.

^P     _Ж ,у е 5 _п (1)"^У "^p ’ ^P || h || _p 6? ,               PIU1      "² ,

С учетом того, что оптимизация происходит на симплексе, мы выберем p = 1. Не сложно показать, что этот выбор оптимален. В результате получим, что Ri =4,

L ₁ = max || A^ || 2 6 2.

г =1 ,...,п

Таким образом, чтобы / ( xn ) 6 £ 2 /2 достаточно сделать N = 32 е ^{- 2} итераций. В действительности, число 32 можно почти на порядок уменьшить немного более тонкими рассуждениями (детали мы вынуждены здесь опустить).

Сделав дополнительные вычисления стоимостью О(п), можно так организовать процедуру пересчета V/(хк) и вычисления arg min д/(хк )/дхг, что каждая итерация будет иметь г=1,...,п сложность О (s2 ln(2 + n/s2)). Для этого вводим к-1

Р к = П(1 — 7 г ), - к = Х к /Р к , 7 к = 7 к /Р к +1 .

г =1

Тогда итерационный процесс можно переписать следующим образом:

^ к +1 — ^ к ^{+ 7} к ^у к .

Пересчитывать АтAzk+1 при известном значении Ат Azk можно за О (s2 ln(2 + n/s2)). Далее, задачу гк+i = argmin df (хк+і)/дхг г=1,...,п можно переписать как гк+і = argmin(ATAzk+1)г.

i =1 ,...,n

Поиск i _k +i можно также осуществить за O(s² ln(2 + n/s ² )). Определив в конечном итоге z n , мы можем определить xn , затратив дополнительно не более

О(п + ln N ) = O(n)

арифметических операций. Таким образом, итоговая оценка сложности описанного метода будет

О ^n +

s ² ln(2 + n/s ² ) E ²

.

Стоит отметить, что функционал, выбранный в этом примере, обеспечивает намного лучшую оценку || Ах || 2 6 E по сравнению с функционалом из раздела 4, который обеспечивает лишь || Ах || ^ 6 E. Наилучшая (в разреженном случае без условий на спектральную щель матрицы Р [6]) из известных нам на данный момент оценок

O(n + s lnn ln(n/^)/s ² )

(см. раздел 4) для || Ах || ^ может быть улучшена приведенной в этом разделе оценкой, поскольку || Ах || 2 может быть (и так часто бывает) в ~ Пр раз больше || Ах || ^ , а s ^ Vn.

• 4.    Седловое представление задачи PageRank и рандомизированный зеркальный спуск в форме Григориадиаса–Хачияна

Перепишем задачу поиска вектора PageRank следующим образом:

^{f ( х )} = ^Ах _х ^ min x e s „ (i)

Следуя [18], эту задачу можно переписать седловым образом:

min max ( Ах, у ) . x e ^s „ ⁽¹⁾ || y || i 6 i

В свою очередь последнюю задачу можно переписать как min max (Ах,Аш\, $GS„(i) weS2„(i)

где

J = [I n , - I n \.

В итоге задачу можно переписать, с сохранением свойства разреженности, как min max (ш,Ах).

x G S „ (1) w G S 2 „ (1)

Следуя [20], опишем эффективный и интерпретируемый способ решения этой задачи. Пусть есть два игрока А и Б. Задана матрица (антагонистической) игры А = ||а.у||, где |aij| 6 1, atj — выигрыш игрока А (проигрыш игрока Б) в случае, когда игрок А выбрал стратегию г, а игрок Б - стратегию j. Отождествим себя с игроком Б. И предположим, что игра повторяется N ^ 1 раз (это число может быть заранее неизвестно [20], однако для простоты изложения будем считать это число известным). Введем функцию потерь (игрока Б) на шаге к:

fk(ж) = <шк,Аж), ж € Sn(1), где wk € ^2п(1) — вектор (вообще говоря, зависящий от всей истории игры до текущего момента включительно, в частности, как-то зависящий и от текущей стратегии (не хода) игрока Б, заданной распределением вероятностей (результат текущего разыгрывания (ход Б) игроку А неизвестен)) со всеми компонентами, равными 0, кроме одной компоненты, соответствующей ходу А на шаге к, равной 1. Хотя функция fk(ж) определена на единичном симплексе, по «правилам игры» вектор ж/г имеет ровно одну единичную компоненту, соответствующую ходу Б на шаге к, остальные компоненты равны нулю. Обозначим цену игры (в нашем случае С = 0)

С = max min (ш,Аж~) = min max (ш,Аж'¹) (теорема фон Неймана о минимаксе). wgS 2 „ (i) $ e s „ (i) $ e s „ (i) wgS 2 „ (i)

Пару векторов (ш,ж), доставляющих решение этой минимаксной задачe (т.е. седловую точку), назовем равновесием Нэша. По определению (это неравенство восходит к Ханнану [26])

1 N min — > fk(ж) 6 С.

$gs„(i) N k=1

Тогда, если мы (игрок Б) будем придерживаться следующей рандомизированной стратегии (см., например, [6], [19], [20]), выбирая { ж ^/г} :

• 1)    р ¹ = (п ¹ ,..., п ¹ ).

• 2)    Независимо разыгрываем случайную величину j(k) такую, что Р(j (к) = j) = p k .

• 3)    Полагаем ж^ = 1, .Р = 0, j = j(k).

• 4)    Пересчитываем

  k +1 ^рз

  
  

k (   /2ЫП ~          ,

.,п,

Рз exP                 • Qi(k)3), 3 = 1, где г(к) — номер стратегии, которую выбрал игрок А на шаге к;3

то с вероятностью >  1 — а

1 ^N                 1 ^N          Р>

N Е fk ж)—^ N £Л (ж) 6 VN — +2V2in(a-1)), т.е. с вероятностью > 1 — а наши (игрока Б) потери ограничены:

N У f _k( х ^к ) 6 С + Д <^V^ + 2^21n(a ^{- 1} )\ ^V к=1                 ^v \                        /

Самый плохой для нас случай (с точки зрения такой оценки) — это когда игрок А тоже действует (выбирая {ш ^к } ) согласно аналогичной стратегии (только игрок А решает задачу максимизации). ⁴ Если и А и Б будут придерживаться таких стратегий, то они сойдутся к равновесию Нэша (седловой точке), причем довольно быстро [20]: с вероятностью 1 — ст:

0 6 || Аx ^N || ^ = max ( w,Ax ⁿ ) — max min (ш,Ах^х) 6 max (w,Ax ^N ) — min (w ^N ,Ах) 6 w e S a n (i)              w e S 2 n (i) $gs „ (i)             w e S 2 n (1)              ^ e s „ (1)

• 1    vi

• 6 max (ш, Axn) — — У(шк, Ахк) + — У Шк, Ахк) — min (wN, Ах) 6 weS2™(1) ,     ' N ^ 1     ' N У,х        '   $Gs„(1)X ,   7

к=1к

6 VN(Vln(2n) + 2 ^ 21п(2 /ст ) ) + -^N(V^ + 2^2Ы(2/ст)) 6

6 2Д(^ln(2n) + 2^2ln(2/^)), где

1 N1 xN = 1 ухк, шN = 1 ушк. NN к=1

Таким образом, чтобы с вероятностью >  1 —ст иметь || АX ^N || ^ 6 е, достаточно сделать

_N = _i6ln(2n)+81n(2/ ^CT ) е ²

итераций;

О^п +

s 1nn(1nn + 1п( ст ¹ ))

е ²

)

— общее число арифметических операций,

где число s ^ ^п — ограничивает сверху число ненулевых элементов в строках и столбцах матрицы Р .

Нетривиальным местом здесь является оценка сложности одной итерации O(s 1nn). Получается эта оценка исходя из оценки наиболее тяжелых действий шаг 2 и 4. Сложность тут в том, что чтобы сгенерировать распределение дискретной случайной величины, принимающей п различных значений (в общем случае) требуется О(п) арифметических операций — для первого генерирования (приготовления памяти). Последующие генерирования могут быть сделаны эффективнее — за O(lnn). Однако в нашем случае есть специфика, заключающаяся в том, что при переходе на следующий шаг s вероятностей в распределении могли как-то поменяться. Если не нормировать распределение вероятностей, то можно считать, что остальные вероятности остались неизменными. Оказывается, что такая специфика позволяет вместо оценки О(п) получить оценку O(s 1n п).

Замечание. Опишем точнее эту процедуру. У нас есть сбалансированное двоичное дерево высоты O(1og 2 п) с п листом (дабы не вдаваться в технические детали, считаем, что число п — есть степень двойки, понятно, что это не так, но можно взять, скажем, наименьшее натуральное т такое, что 2 ^т > п, и рассматривать дерево с 2 ^т листом) и с О(п)

., 2м,

общим числом вершин. Каждая вершина дерева (отличная от листа) имеет неотрицательный вес, равный сумме весов двух ее потомков. Первоначальная процедура приготовления дерева, отвечающая одинаковым весам листьев, потребует О(п) операций. Но сделать это придется всего один раз. Процедура генерирования дискретной случайной величины с распределением, с точностью до нормирующего множителя, соответствующим весам листьев, может быть осуществлена с помощью случайного блуждания из корня дерева к одному из листьев. Отметим, что поскольку дерево двоичное, то прохождение каждой его вершины при случайном блуждании, из которой идут два ребра в вершины с весами а > 0 и b >  0, осуществляется путем подбрасывания монетки («приготовленной» так, что вероятность пойти в вершину с весом а — есть а/(а + b)). Понятно, что для осуществления этой процедуры нет необходимости в дополнительном условии нормировки: а + b = 1. Если вес какого-то листа алгоритму необходимо поменять по ходу работы, то придется должным образом поменять дополнительно веса тех и только тех вершин, которые лежат на пути из корня к этому листу. Это необходимо делать, чтобы поддерживать свойство: каждая вершина дерева (отличная от листа) имеет вес, равный сумме весов двух ее потомков.

Итак, выше в этом разделе была описана процедура генерирования последовательности х ^к со сложностью

О(п + 8 ln П ln(n/u)/E2), на основе которой можно построить такой частотный вектор:

1 N = і?      , к=1

компоненты — частоты, с которыми мы использовали соответствующие стратегии, что || Аж ^ || ^ 6 Е с вероятностью >  1 — ст.

• 5.    Программная реализация

• 5.1.    Хранение разреженной матрицы

• 5.2.    Поиск минимального/максимального компонента градиента

Рассматриваемые в работе методы реализованы авторами в рамках единой программной системы на языке C++. Работоспособность и корректность реализации проверена с использованием компиляторов GCC (GNU Compiler Collection, версии: 4.8.4, 4.9.3, 5.2.1), clang (C language family frontend for LLVM, версии: 3.4.2, 3.5.2, 3.6.1, 3.7.0), icc (Intel C Compiler, версия 15.0.3) на операционных системах GNU/Linux, Microsoft Windows и Mac OS X.

Для удобства введем следующие обозначения рассматриваемых в работе методов: NL1 — метод из раздела 2, FW — метод из раздела 3 и GK — метод из раздела 4.

Для хранения данных разреженной матрицы А используется широко распространенный формат CSR (Compressed Sparse Row), позволяющий работать с матрицами произвольной структуры. Поскольку для рассматриваемых методов существует необходимость обращения к элементам как матрицы А (вычисление функции), так и матрицы А^т (вычисление градиента), в текущей программной реализации осуществляется хранение в памяти обеих матриц. Это, естественно, влечет за собой удвоение объема потребляемой оперативной памяти, но радикальным образом улучшает быстродействие соответствующих вычислительных процедур.

Методы NL1 и FW требуют наличия информации о минимальной/максимальной компоненте градиента — номере (индексе) соответствующей переменной. Поскольку идеология методов подразумевает выполнение большого числа «легких» итераций, поиск таких компонент должен быть эффективно реализован. С учетом того, что все рассматриваемые методы учитывают разреженность решаемой задачи и в итоге производят модификацию конечного (и весьма небольшого относительно п) числа компонент градиента, в текущей реализации применяется подход, предложенный в работе [4]. Основной его идеей является построение бинарного дерева, реализующего вычисление требуемой функции от п переменных (в нашем случае — min/max), и механизм быстрого обновления (за O(lnп)) вычисленного ранее значения в случае изменения одной переменной (вместо «полного» поиска за О(п)).

Реализация таких деревьев выполнена в виде шаблонных классов C++, что позволяет задавать требуемую функцию – обработчик данных на этапе компиляции и обеспечивает максимальное быстродействие при вызове этой функции относительно других вариантов реализации: функторов (std::function + lambda), указателей на функцию или применение виртуального метода.

Длина обрабатываемого деревом вектора в общем случае не равна степени двойки, поэтому реализованные классы деревьев создают при необходимости дополнительные узлы на соответствующих уровнях и при обработке данных учитывают это обстоятельство, напрямую «проталкивая» данные таких «некратных» узлов на вышестоящий уровень для последующей обработки.

Поскольку используемые в работе деревья должны реализовывать не только поиск ми-нимального/максимального значений градиента, но и соответствующего им индекса, то в каждом узле такого дерева хранятся и обрабатываются пары «индекс–значение». Такой подход увеличивает объем памяти, занимаемый деревом, но существенным образом улучшает его быстродействие, поскольку исключается необходимость обращения в общем случае к случайным элементам вектора градиента, что весьма затратно с точки зрения работы кэша современных процессоров. Такое «совместное» хранение пар «индекс–значение» существенно улучшает «локальность» данных для процессора при обработке узлов.

Также для рассматриваемых деревьев реализован механизм отсечений — если получаемый функцией-обработчиком результат от данных с «дочерних» узлов не меняет содержимое текущего узла, то, очевидно, дальнейшее «продвижение» на вышестоящие уровни не имеет смысла и будет бесполезной тратой времени и вычислительных ресурсов. Применение этого механизма на практике показало его полную оправданность — например, при решении методом FW задачи web-Google (см. ниже) с числом переменных п = 875 713, полная высота дерева поиска минимального компонента градиента равна 20 (2 19 < п < 2 ²⁰ ), а средняя «высота работы» алгоритма обновления этого дерева при наличии механизма отсечений — 5.

• 5.3.    Генерация дискретной случайной величины с требуемой вероятностью

• 5.4.    Вычисление значения функции

Для работы метода GK требуется наличие генератора дискретной случайной величины с требуемой вероятностью (алгоритм такой генерации подробно изложен в разделе 4). Реализация требуемого дискретного генератора выполнена с использованием вычислительных деревьев, описанных в разделе 5.2. Отличие в реализации состоит в том, что дерево для рассматриваемого генератора реализует функцию суммирования вероятностей и работает не с парами «индекс–значение», а напрямую со значениями (вероятностями). Также выполнена оптимизация алгоритма генерации — достаточно всего лишь одного подбрасывания монетки для поиска нужного листа (переменной): генерируем случайную величину 0 6 г 6 р , где р — значение вероятности в корневом узле; начиная с корневого узла, проверяем условие г 6 р _а , где р _а — значение вероятности в «дочернем» узле а; если условие выполняется — переходим на узел а, в противном случае вычисляем г = г — р _а и переходим на «дочерний» узел Ь; процедуру выполняем до тех пор, пока не достигнем требуемый нам лист (переменную).

Наличие значения функции в текущей точке для рассматриваемых методов, вообще говоря, не требуется. Но данная информация может быть полезна в качестве критерия останова, для построения графика сходимости метода и т.п. Для вычисления (обновления) значения функции можно применить подход с использованием деревьев из раздела 5.2, реализующих операцию суммирования, но это влечет за собой дополнительные вычислительные расходы (O(lnп) на каждое обновление). Поэтому в текущей реализации для методов NL1 и FW используется прямое обновление суммы:

п

/ к = У? b ² , где 6 = ^Аж к • i =1

Рассматриваемые методы в процессе своей работы производят изменение отдельных элементов вектора ж к на некоторую величину Аж, что влечет за собой изменение s элементов вектора 6:

Ab i = A tj • Аж- j .

Зная эту величину мы можем обновить значение оптимизируемой функции:

/ + = / к + 2b i Ab i - (Ab i ) ² .

Для метода FW требуется сделать уточнение. Нетривиальным моментом, позволившим существенно увеличить скорость его работы, стало избавление от линейной (за О(п)) операции масштабирования вектора жк на каждой итерации (см. раздел 3). Рассмотрим этот подход более подробно. Пусть жі — стартовая точка, тогда

Ж 2 = (1 - 7 і )ж і + 7 1 У 1 = У 1 — т.к. 7 1 = 1,

Жз = (1 - 72^2 + 72У2 = (1 - 72)(ж2 + 2 2У2), ж4 = (1 - 73)ж3 + 73У3 = (1 - 72)(1 - 7з) (ж2 +  '22У2 + (1-72Х1-73)Уз) ,

̂︀ жк+1   Рк

̂︀

к

(^ж 2 ⁺ Е 7іу/) = /Зк ^У 1 ⁺ Е ⁷ i у/)

̂︀

̂︀

З к ^ж к ,

где / к = П (1 - 7 т ), 7 к = 7 к (Р к .

т =2

Вполне очевидно, что мы можем (разреженно) обновлять содержимое вектора ж к

ука-

занным образом на каждой итерации. Актуальным становится вопрос такого учета коэффициента /к, который не нарушает разреженность и позволяет осуществлять вычисление (пересчет) функции/градиента на каждой итерации алгоритма. Считаем, что у нас уже есть вычисленное значение функции/градиента (рассматриваем задачу ||Аж||2) в некото- рой точке, тогда

• 1)    В случае изменения (путем умножения на некоторое а) коэффициента /3, значение функции пересчитывается как

  / ⁺ = « ² /.

Значение компонент градиента, соответственно, должно быть масштабировано на а, но, т.к. метод не требует собственно значений компонент, а только индекс минимального элемента, эту процедуру можно опустить. Если же требуется значение нормы градиента (например, в качестве одного из критерия остановки), то она пересчитывается очевидным образом:

Н^а 9Н2 = ^аН 9Н2.

• 2)    В случае изменения какой-либо компоненты вектора X (без изменения значения 3) на некоторое Аж ^ производится обновление s элементов вектора b = Аж на величину

• 6.    Численные эксперименты

Ab _j = А^ • Ax j = А ^ • Ax j .

Для каждого такого Abj обновляется значение функции f + = f + 32(2bjAbj - (Abj)2)

и s компонент градиента д

Ag _k = А ^ • Ab j = А к • Ab j .

Таким образом, в процессе работы метода непосредственное умножение X на коэффициент 3 (что требует О(п) операций) не производится, эта операция осуществляется только в конце, когда необходимо вернуть «истинное» значение оптимизируемых переменных ж * = 3n • Xn . Применение описанного подхода позволило существенным образом увеличить быстродействие реализованного алгоритма.

Проведенные вычислительные эксперименты показали, что представленные схемы прямого обновления суммы (вместо применения деревьев) не ведут к каким-либо значительным накоплениям ошибок округления. После завершения процедуры минимизации для проверки производилось «честное» вычисление f (ж * ).

Приводимые в работе результаты численных экспериментов получены на вычислительной системе, имеющей следующие характеристики:

• •    ubuntu server 14.04, x86_64,

• •    Intel Core i5-2500K, 16 Гб ОЗУ,

• •    используемый компилятор — gcc-5.2.1,

параметры сборки: -std=c++11 -O2 -mcmodel=small -DNDEBUG .

Поведение рассматриваемых методов исследовалось на задачах PageRank различной размерности с матрицами 3-х типов:

• 1)    диагональная, с задаваемым числом диагоналей: п д = 1,3,5,... Каждая стро-ка/столбец матрицы содержит (п д — 1)/2 + 1 6 s 6 п д ненулевых элементов;

• 2)    со случайно генерируемой структурой. Каждая строка/столбец матрицы содержит ровно s ненулевых элементов;

• 3)    построенная из web-графов, загруженных с сайта Стэнфордского университета [27]. Строки/столбцы матрицы А содержат произвольное число ненулевых элементов (см. табл. 1).

Для всех проводимых экспериментов задавалось значение е = 10 - 4 . Для методов NL1 и FW в качестве стартовой точки выбрана первая вершина единичного симплекса ж о = (1, 0,..., 0), критерий остановки — f (ж _к ) = 1/2 || Аж ^ || 2 6 е ² /2. Метод GK останавливался по достижению требуемого числа итераций (А), после завершения алгоритма производилась проверка || Aх ^N || ^ 6 е.

Указанное в результатах время отражает только работу метода оптимизации, т.е. не включает в себя загрузку/генерацию А/А^т , инициализацию деревьев, первоначальное «полное» вычисление функции/градиента и т.п.

Таблица1

Характеристики матрицы А для задач с web-графами

web-graph			Число ненулевых элементов
			в строке		в столбце		среднее
			мин.	макс.	мин.	макс.
Stanford,	п	= 281903	2	38607	1	256	9.2
NotreDame,	п	= 325729	2	10722	1	3445	5.51
BerkStan,	п	= 685230	1	84209	1	250	12.09
Google,	п	= 875713	1	6327	1	457	6.83

Проведенные вычислительные эксперименты позволили сделать следующие выводы:

• 1)    К сожалению, реализация метода GK показала неудовлетворительные результаты — авторам так и не удалось достичь стабильного выполнения условия || Аж ^ || ^ 6 е. Поиск причин подобного поведения привел к интересным наблюдениям. Добавление вычисления функции на итерациях (что изначально не требуется и существенно снижает быстродействие) показало, что метод довольно быстро спускается в точку, которая в ряде случаев удовлетворяет требуемому условию, но после этого значение функции начинает расти и метод приходит в точку x ^N , где требуемое условие нарушено. Попытки разобраться с причиной такого поведения выявили, что в процессе оптимизации ряд компонент векторов р г и p j принимают очень большие значения, вплоть до машинной бесконечности в случае выполнения достаточно большого числа итераций. Очевидно, что такие значения вероятностей приводят к тому, что генератор псевдослучайных чисел просто не может “попасть” в остальные “маленькие” компоненты, которые в итоге оказываются исключены из процесса оптимизации, а метод оперирует переменными только из весьма небольшого множества. Выполнение периодического перемасштабирования векторов р г и p j (так, чтобы сумма их компонент стала равна 1) не изменили наблюдаемое поведение. Так же было замечено, что рассматриваемый эффект несколько ослабевает с увеличением значения N , но не исчезает полностью, а лишь сдвигается во времени — см. рис. 1.

f(x)

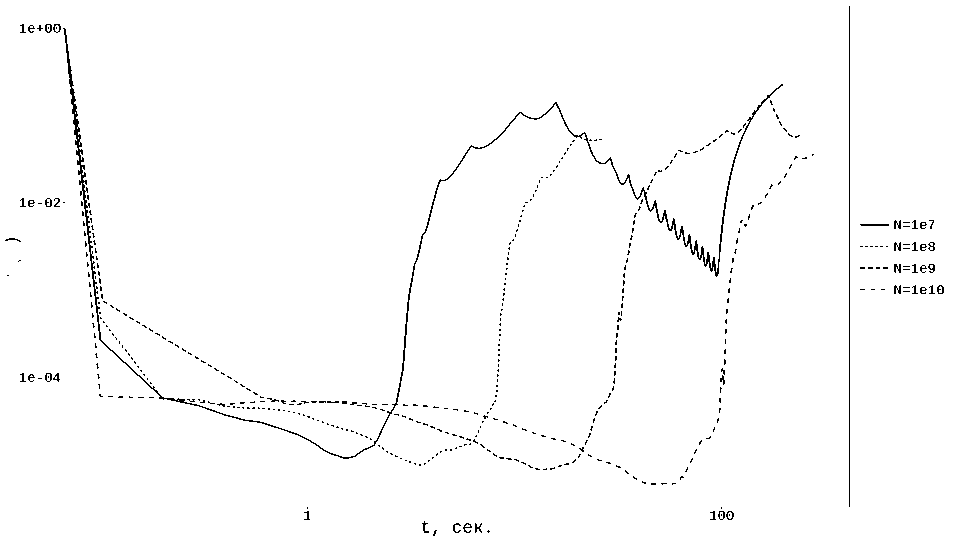
Рис. 1. Поведение метода GK при различном значении N, А — случайная, п = 10 2 , s = 3

Разумным объяснением этому неприятному факту, на наш взгляд, может быть машинная арифметика, вносящая свой вклад в виде накопления погрешностей, а также «неидеальная» (с точки зрения математики) работа генератора псевдослучайных чисел (хотя в реализации используется хорошо проверенный на практике генератор MersenneTwister). Мы вынуждены констатировать, что хорошие теоретические оценки для метода GK пока дали весьма посредственные практические результаты.

• 2)    Быстродействие методов на задачах с диагональной матрицей А (см. табл. 2, рис. 2) существенно выше (особенно это касается метода FW), чем в случае постановок со случайной А (см. табл. 3, рис. 3). Это связано с тем, что кэш центрального процессора при работе с диагональной матрицей работает в существенно более «комфортных» условиях, поскольку производятся последовательные операции чтения/записи смежных элементов векторов ж и b = Аж. Операции обновления деревьев поиска ми-нимального/максимального компонент градиента также осуществляются в смежных компонентах. Структура диагональных матриц такова, что обработав одну строку матрицы, мы получаем в кэше такой набор компонент векторов ж и b, что обработка следующей строки почти не потребует обращения к ячейкам оперативной памяти, причем этот эффект практически не зависит от размерности задачи (при фиксированном пд). Это хорошо видно на примере постановок с s = 3 — при росте размерности задачи на 5 порядков имеем рост времени работы алгоритма не более чем на 50%.

103 529.240 5216119 1.552 46447 104 535.348 5216119 1.045 29991 105 537.419 5216119 1.741 49235 106 549.782 5216119 1.758 49235 107 552.271 5216119 1.789 49235 пд = 101; 51 6 s 6 101

10⁴

1935.198

5175085

6.464

49925

10⁵

1962.307

5175085

9.097

68646

10⁶

1940.331

5175085

9.134

68646

Таблица2

Время (с) решения задачи PageRank, А — диагональная

п метод NL1 метод FW время итерации время итерации пд = 3; 2 6 s 6 3 102 4.089 3948632 0.007 14142 103 4.221 3950392 0.008 14142 104 4.575 3950392 0.009 14142 105 4.814 3950392 0.010 14142 106 5.143 3950392 0.010 14142 107 5.566 3950392 0.010 14142 108 6.021 3950392 0.010 14142 пд = 11; 6 6 s 6 11 102 14.655 2100964 0.041 14749 103 37.796 5101072 0.041 16956 104 39.170 5101072 0.062 19995 105 39.897 5101072 0.064 24495 106 41.004 5101072 0.065 24495 107 43.917 5101072 0.068 24495 пд = 51; 26 6 s 6 51

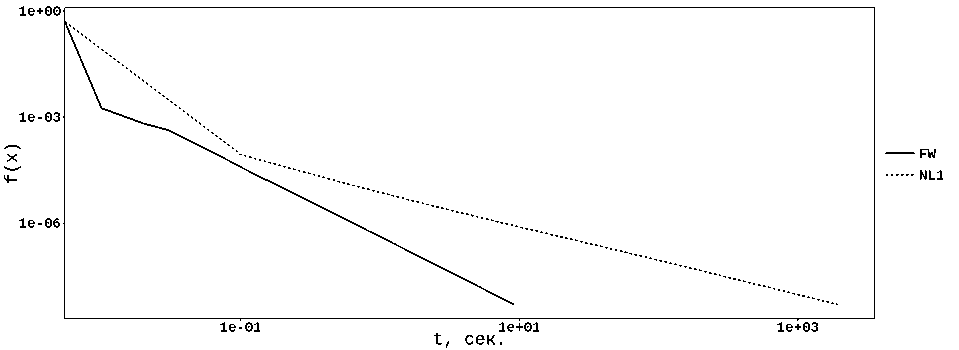
Рис. 2. Решение задачи PageRank, Л — диагональная, п = 10 6 , п ^ = 101

Для матриц со случайной структурой начинаются «хаотичные» запросы к ячейкам памяти, что резко снижает эффективность работы кеша, которая в общем случае падает при увеличении п, поскольку растет размер обрабатываемых векторов ж и Ь, которые кэшируются при таких «хаотичных» запросах всё хуже и хуже.

Таблица3

Время (с) решения задачи PageRank, Л — случайная

п	метод NL1		метод FW
	время	итерации	время	итерации
s = 3
10 2	0.003	1999	0.023	39734
10 3	0.031	17748	0.118	190601
10 4	0.233	141739	0.414	632954
10 5	2.374	840617	2.107	2009854
10 6	16.171	4020388	9.355	6203826
10 7	56.694	11669495	32.442	17916520
10 8	173.070	19988053	121.258	43390838
s = 11

102 0.013 590 0.173 44706 103 0.072 5106 0.593 142109 104 0.568 40029 2.123 450873 105 6.342 299382 10.374 1482735 106 78.383 2025423 60.715 4753809 107 503.385 11272158 219.988 14693667 s = 51 103 0.891 3851 11.681 162015 104 8.383 31372 42.824 510444 105 77.137 241191 164.751 1621686 106 1300.194 1683845 1152.805 5082774 107 11250.461 10627974 5432.107 17479622 s = 101

10 4	29.540	29127	168.124	529685
10 5	304.419	225146	650.878	1696708
10 6	4692.729	1607834	4619.220	5267738

f(x)

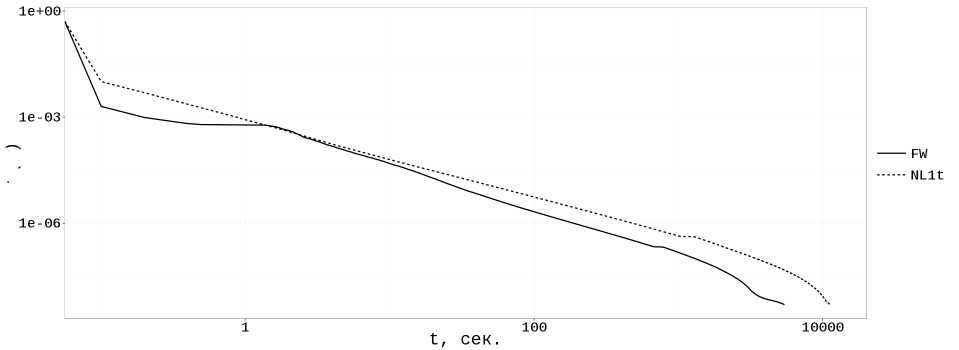
Рис. 3. Решение задачи PageRank, Л — случайная матрица, п = 10 7 , s = 51

• 3)    Весьма неожиданным эффектом стало быстродействие метода FW для задач с web-графами (см. табл. 4, рис. 4 и 5). Проведенные эксперименты показали, что число итераций, потребовавшихся для получения решения с требуемой точностью, для всех таких постановок оказалось меньше , чем размерность задачи.

Метод NL1 на 2-х задачах этого типа, к сожалению, показал весьма посредственные результаты, что, на наш взгляд, связано с тем, что он модифицирует 2 переменных за итерацию (в отличие от метода FW), причем выбирает эти переменные таким образом, что регулярно попадает на ««неудачные» строки/столбцы матрицы Л. Поясним этот момент более подробно. В табл. 1 приведены характеристики разреженности матрицы Л, где отражено, что существуют ««длинные» строки/столбцы (с большим s), выбор которых на итерации влечет за собой существенный объем вычислений. Метод NL1 в процессе работы регулярным образом выбирает эти «длинные» строки/столбцы, что дает очень высокую стоимость соответствующей итерации. Обозначим s _T — число ненулевых элементов в текущей (обрабатываемой методом) строке матрицы Л, s _c — в текущем столбце. Очевидно, что чем меньше эти значения, тем «легче» итерация и выше быстродействие метода. В табл. 5 показаны величины этих параметров, которые показывают, что для задачи web-BerkStan средняя стоимость итерации (оценивается по значению s _T • s _c , т.е. числу обрабатываемых за итерацию элементов матрицы Л) для метода NL1 оказалась на порядок выше, чем у метода FW. При этом для задачи web-Stanford метод NL1 показывает намного более удачный выбор строк/столбцов, показывая результаты, вполне сопоставимые с методом FW. Заметим также, что при решении подобных постановок с «реальной» структурой матрицы Л, отдельные итерации рассматриваемых методов (максимальное значение s _T -s _c в табл. 5) по стоимости могут быть сопоставимы с полным вычислением функции/градиента.

Таблица4

Время (с) решения задачи PageRank для web-графов

web-граф	п	метод NL1		метод FW
		время	итерации	время	итерации
Stanford	281903	0.145	93152	0.008	14142
NotreDame	325729	700.810	3816436	0.526	38014
BerkStan	685230	38161.847	12315700	0.536	19990
Google	875713	113.643	1083996	0.278	37313

Таблица5

Стоимость итерации для задач c web-графами

	Stanford		BerkStan
	NL1	FW	NL1	FW
мин.	1.0	1.0	1.0	1.0
s r макс.	34.0	4.0	84209.0	84209.0
среднее	3.9	3.9	2278.4	148.6
мин.	2.0	2.0	1.0	1.0
s c макс.	37.0	3.0	244.0	83.0
среднее	2.9	2.8	15.7	6.2
мин.	3.0	3.0	2.0	2.0
s r • s c макс.	1258.0	12.0	15494456.0	6989347.0
среднее	11.7	11.3	84304.3	7507.5

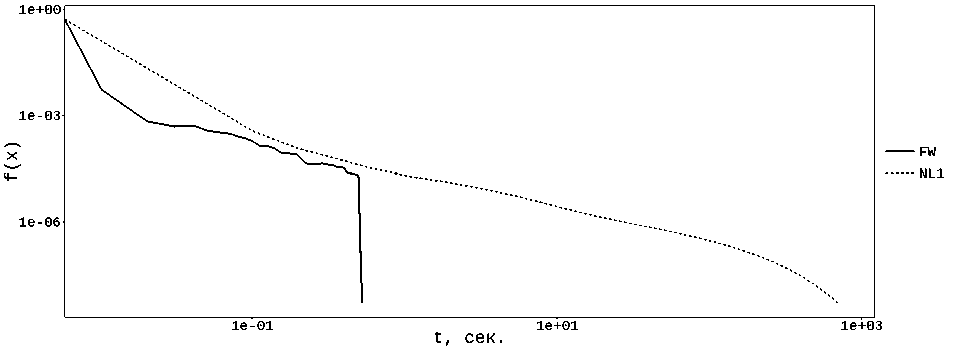
Рис. 4. Решение задачи web-NotreDame

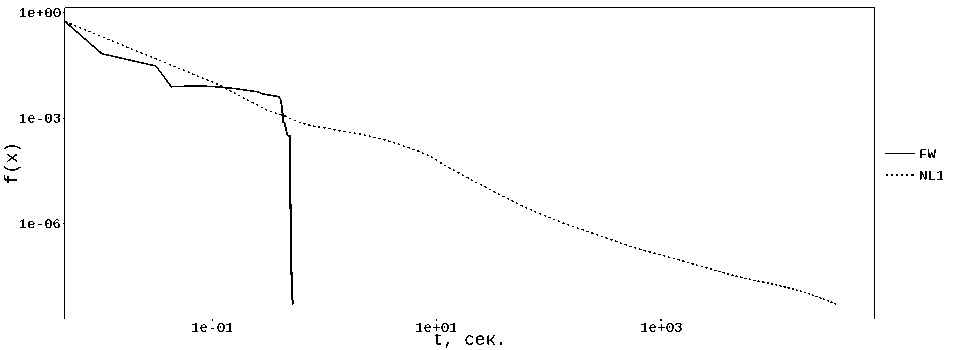
Рис. 5. Решение задачи web-BerkStan

• 7. Заключение

  Данная статья представляет собой запись доклада А.В. Гасникова на Традиционной математической школе Б.Т. Поляка в июне 2015 года. Метод из раздела 2 был предложен Ю.Е. Нестеровым в ноябре 2014 года. Этот метод впоследствии дорабатывался А.В. Гасниковым, А.С. Аникиным, А.Ю. Горновым, Д.И. Камзоловым и

  Ю.В. Максимовым. Подход из раздела 3 был предложен в апреле 2015 А.В. Гасниковым и А.Ю. Горновым. Подход дорабатывался Ю.В. Максимовым. Поход из раздела 4 был предложен А.В. Гасниковым в 2012 году (по-видимому, в это время и был введен класс дважды разреженных матриц в задачах huge-scale оптимизации, при попытке перенести результаты Григориадиса–Хачияна [19] на разреженный случай). Подход дорабатывался А.С. Аникиным. Численные эксперименты проводились А.С. Аникиным и Д.И. Камзоловым.

Исследование авторов в части 4 выполнено в ИППИ РАН за счет гранта Российского научного фонда (проект 14-50-00150), исследование в части 3 выполнено при поддержке гранта РФФИ 15-31-20571-мол_а_вед, исследование в части 2 – при поддержке гранта РФФИ 14-01-00722-а.