Эффективные жесткости гофрированной пластины

Целью данной работы является численная реализация методики осреднения [1] в приложении к задаче изгиба упругих гофрированных пластин, периодических в плане. Использование метода осреднения позволяет вычислить не только эффективные жесткости гофрированной пластины, но и все характеристики напряженно-деформированного состояния благодаря сочетанию решения локальных задач — задач для ячеек периодичности, с решением глобальной задачи для осредненной плоской пластины.

Историю развития асимптотического анализа деформирования неоднородных линейно упругих пластин можно проследить по работам [2–7]. Применение асимптотического метода к задаче изгиба плоской слоистой пластины приводит в первом приближении к уравнениям классической теории слоистых пластин [8], а в случае однородной пластины — к уравнениям теории тонких оболочек Кирхгоффа–Лява. Методика осреднения, совмещенная с линеаризацией, получила распространение на случай нелинейных определяющих соотношений [9].

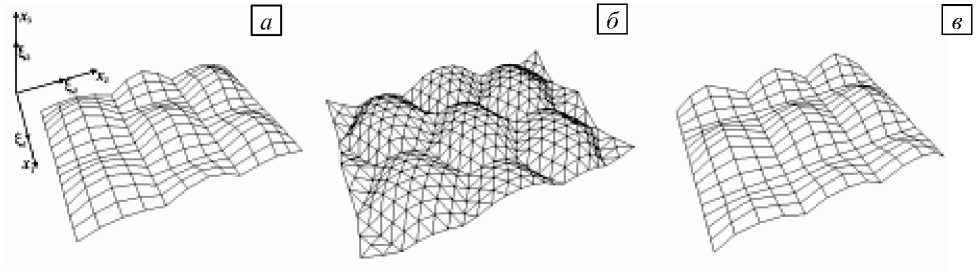
Рис. 1. Периодические в плане пластины: со смещенной четырехугольной ячейкой ( а) , сотовая ( б) , с четырехугольной ячейкой ( в)

Вообще говоря, в гофрированных пластинах периодичность касается не только формы, но и свойств, однако далее в настоящей работе материал рассматриваемых пластин (Рис. 1) полагается однородным. Прежде всего для таких пластин встает вопрос определения эффективных жесткостей. Частично подобная проблема решалась численно и экспериментально в [10] для пластины с шестиугольной ячейкой периодичности. Численное решение получалось путем конечно-элементного моделирования всей пластины, состоящей из большого числа ячеек периодичности. Следует учесть, что у гофрированной пластины жесткости растяжения, изгиба и взаимного влияния различаются на порядки, и, чтобы меньшие из них вычислялись с приемлемой точностью, требуется достаточно мелкая конечно-элементная сетка. Метод осреднения является двухсеточным и позволяет решать как локальную задачу на ячейке периодичности, так и осредненную глобальную задачу для всей пластины, обеспечивая одинаковую точность их решения. Поскольку в методе осреднения для вычисления всех жесткостей периодической пластины достаточно осуществить процедуру расчета только для одной ячейки, использование мелкой сетки не приводит к чрезмерным вычислительным затратам.

Существуют два подхода к осреднению для тонкой упругой гофрированной пластины, периодической в плане. Во-первых, осреднение может применяться к уравнениям трехмерной теории упругости, во-вторых, — к уравнениям теории оболочек. Возможна также комбинация этих подходов. Далее рассматривается только первый подход.

Необходимо отметить, что методика осреднения, применяемая к пластинам, отличается от методики для трехмерной или двухмерной периодической среды [11]. Отличительная особенность заключается в том, что в случае пластин необходимо выполнять граничные условия на лицевых поверхностях пластины.

Формально видоизменение метода осреднения для пластины состоит в том, что перемещения u_i представляются как функции двух медленных координат x ₁, x ₂ в проекции пластины и трех быстрых координат 5 1 , 5 2 , 5 3 в переделах ячейки периодичности; связь между координатами задается соотношениями 5 i = x, £ ■, где £ — некоторый малый параметр: u = u i ( x 1 , x 2 , 5 1 , 5 2 , 5 3 ) , i = 1,2,3. Малый параметр £ связан с размером неоднородности формы пластины (Рис. 2), то есть £ = l(L, где l — характерная длина ячейки периодичности, а L –– характерный размер самой пластины.

Перемещения записываются как u i = u e + u^b b , где u ® — перемещения, связанные c продольными деформациями в отсчетной плоскости пластины, а u_i ^b — перемещения, вызванные изгибом, и представляются в виде рядов:

ui = v ( x 1 , x 2 ^{) +} ^ ^£ N iPQ 0 ... Q m - i ( ⁵ 1 ’ ⁵ 2 ’ ⁵ 3 ) v P , Q o ... Q m _ , ( x 1 , x 2 ) ,

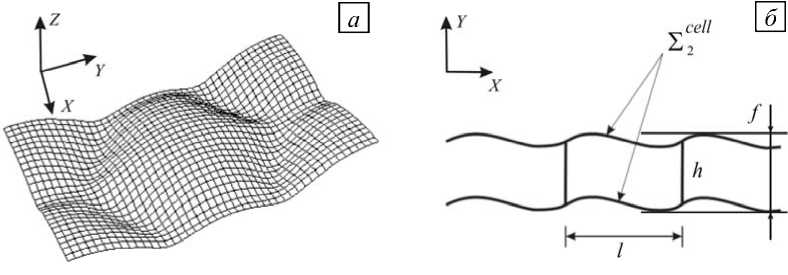
Рис. 2. Ячейка периодичности сотовой пластины: общий вид с нанесенной мелкой сеткой ( а ) и план в плоскости XZ ( б); S 2 ell - суммарная верхняя и нижняя поверхности ячейки, l - длина ячейки

ul     £^3 w, I ( x1’ x2 ) + ^£ N lPQo... Qm-2 (^1’^2 ’^3 ) w, PQo... Qm-2 ( x1’ x 2 X m=2

u 3 = w ⁽ x l ’ x 2 ^{) +} ^ ^{£ N} 3 PQ 0 ... Q m - 2 ⁽^ 1 ’^ 2 ’^ 3 ) w.PQ 0 ... Q m 2 ^{( X} 1 ’ ^X 2 ^

m = 2

первые члены которых аналогичны перемещениям, возникающим в однородной плоской пластине: v1, v2 — медленно меняющиеся перемещения в отсчетной плоскости, v3 = 0, w — прогиб, Ne    –– локальные функции, соответствующие состоянию растяжения в iPQ0...m плоскости пластины, NibPQ ...Q –– локальные функции изгиба. Здесь и далее используются обозначения, принятые в работе [5]; буквенные индексы P,Q0,...,Qm,I пробегают значения 1, 2, а индексы i,j,k,l — значения 1, 2, 3; в зависимости от контекста символом «,» обозначается частная производная по xI, где l = 1,2, или по £i, где i = 1,2,3 .

Формулы (1), (2) позволяют выразить напряжения в виде:

° у   PjPQ0 vP, Qo +^£ PjPQo... QmvP, Qo... Qm ’ m =1

e iPQo      iJPQo + jkiN kPQo ’ l , ee

^QjPQ o =-^ 3 ^CiJPQ o ⁺ C jkl N kPQ o ’ l ^

bb

где C_ijkl –– упругие модули пластины. При учете первых четырех слагаемых в

приближении ( m = 3) однородные уравнения равновесия выглядят следующим образом:

° iJ , J   _£ P iJPQo, J v P , Q o

iQPQ o ⁺ P JPQ o Q , J ) v P , Q o Q ^{+ Q}iJPQ o , J w PQ o ^+£ ( ^Qi Q PQ o ^{+ Q}iJPQ o Q 1 , J ) w , PQ o Q 1 ⁺

+£( P ee PQ + PjPQQQ jVpqqq +£ ²( Q ee pq + Qupqqq ^pqqq = o. iQ ₂ Q ₁ PQ ₀      ijPQ ₀ Q ₁ Q ₂, j P , Q ₀ Q ₁ Q ₂           iQ ₂ Q ₁ PQ ₀       ijPQ ₀ Q ₁ Q ₂, j , PQ ₀ Q ₁ Q ₂

В первом приближении локальные задачи (задачи на ячейке периодичности V ^cell ) строятся таким образом, чтобы обнулялись коэффициенты при производных v_P , _Q и w , _PQ

(поскольку в первом приближении остается только производная по переменной с индексом Q ₀ , то далее индекс «0» опускается). Эти задачи формулируются следующим образом:

P PQ , j = 0, Q ijPQ , j = 0,     ”e V ,

PjPQnj = 0,   QyPQnj = 0,    ” e ST, где n — вектор внешней нормали к поверхности ячейки, S2e11 — верхняя и нижняя поверхности ячейки. Вся же граница Sce11 состоит из двух частей: Sce11 = S2e11 + Sa^, причем S2e11 = Stop + Sbot есть сумма верхней и нижней лицевых поверхностей, как показано на рисунке 2. На боковых поверхностях ячейки периодичности S C^ral ( ”I = ± 1/ /2, I = 1, 2) ставятся условия периодичности, имеющие вид:

N ^e

^iPQ ” а = 1 а /2

e

N iPQ а„=- 1 а /2 ,

e

C ijk1 N kPQ , 1 n j а_а= 1 а /2

e

C y^ N kPQ , 1 n j а^- 1 а /2 ,

b

N ^iPQ ” „ = 1 а /2

b

N ^iPQ ” „ =- 1 а /2 ,

jjki N kPQ , n а_а= 1 а /2

b

C ijk N kPQ , n §_а=_ 1 а /2 ^.

Проекция ячейки периодичности на отсчетную плоскость есть прямоугольник со сторонами 1 1 , 1 ₂. Его площадь S ^ce11 в переменных х 1 , x ₂ равна 1 1 1 ₂ или а ² 1 ^ а 1 ₂ ^а , где 1 1 ^а и 1 2” — стороны ячейки периодичности в переменных ^ i , а ₂ • Индексы P и Q в локальных краевых задачах (6), (7) –– свободные параметры, принимающие значения 1, 2.

Для вычисления всех локальных функций N_i ^e _PQ и N_i ^b _PQ требуется решить 6 локальных задач с краевыми условиями свободной границы (6) на верхней и нижней поверхностях и условиями периодичности (7) на боковой поверхности. Условия периодичности являются следствием периодичности структуры и означают, что перемещения, напряжения и деформации представляются в виде медленно изменяющихся составляющих, на которые наложены быстро меняющиеся периодические флуктуации. Может показаться, что периодичность структуры является необходимым условием для применения метода осреднения. В действительности это не совсем так, однако периодичность вносит в процесс вычислений существенное упрощение. Поскольку все ячейки одинаковы, то достаточно решить локальную задачу только на одной ячейке. Если локальная задача зависит от медленных координат как от параметров, то она решается независимо для каждой ячейки. Такая ситуация возникает, например, в нелинейных задачах [9].

Краевые задачи (6), (7) можно решить несколькими способами. Выбор способа зависит от толщины листа h , из которого получена гофрированная пластина. Отношение толщины h к длине ячейки периодичности 1 есть второй (наряду с а ) малый параметр задачи в = h/1 . Если в ~ 1, то задачи на ячейке периодичности являются трехмерными и для их решения следует применять МКЭ с трехмерными элементами. Если в <<  1, то ячейка периодичности представляет собой тонкое тело и для решения локальных задач можно применять МКЭ с оболочечными конечными элементами.

Разрешающее уравнение теории периодических в плане пластин получается из уравнений равновесия усилий и моментов так же, как в теории пластин с плоскими поверхностями. Эти уравнения для произвольной периодической в плане пластины следуют из трехмерных уравнений равновесия [1], если используется определение усилий и моментов, данное в [5]. Исходя из идеи двух масштабов, упругие уравнения равновесия для пластины можно записать в следующем виде:

° IJ , x J ⁺ ( V ⁸ ) ° Ij_Aj = ⁰,      ° 3 J , x J ⁺ ( V ⁸ ) °3^ = ⁰

( I , J = 1,2; i , j = 1,2,3 ) .

Интегрирование соотношений (8) по ячейке

периодичности с учетом того, что

° ij = ° ij ( X 1 , x 2 , , 1 , , 2 , , 3 ) , дает следующее уравнение: -1^ ^T ,

cell

cell

^8T , T o

T c^dl = l p 1 2 . Переход к записи в усилиях

N f ° dV = J- f ° dV ,

IJ     у cell J IJ , у cell J IJ ’

T , ^ceil                T      v cell

T cell _ i 1 1 2 _ _£ ² T c^el1 приводит уравнения равновесия к виду: N_IJ J

+ ^ J S i ( x . С ) d ^Т    0.

^Т , T o

Аналогично (см. [1]) получаются выражения для моментов и перерезывающих сил:

M u = J . J ^x 3 ° iJ^dV ,

^T     v“¹¹

+, =     j °.₃ dV . Остальные уравнения равновесия имеют

Т cell V e

вид [1]: M_IJJ + Q_I = 0, Q_II + p ( x ) = 0 (в данной работе p отвечает значение 8 ³ p из

„ п                    е    (Sj, I = 1, 2         _ статьи [1]). Здесь Si = {S, i = 1 2 3 — поверхностные силы.

При рассмотрении задачи поперечного изгиба пластины предполагается, что J S_I d Т , = 0 . Например, этот интеграл равен нулю, если пластина нагружена давлением. Т₆ '° ^Р

В более общем случае можно обозначить f ( x ) = —^ S_I ( x , С ) dV, .

ТГ    '

получаются 5 уравнений равновесия:

В итоге

N

M

Qu + Р ( x ) = ⁰

В первом приближении напряжения записываются в виде

° ij    P ijPQ v P , Q ^{+ 8 Q}ijPQ w, PQ •

Интегрирование (10) с учетом предыдущих выражений усилий и моментов дает определяющие соотношения для осредненной пластины:

N = Д         R ⁽¹⁾

¹ ' IJ   iJp+P e f'P Q +    i.Q' O ^к PQ ,

М = В ⁽²⁾ е + D к

1V1 ij ui.+e>pQ>+ + IjPqpq к pq , где epn = vp,.; кРГ1 =-w,РГ). При этом жесткости на растяжение A,,p,, на изгиб Dnpn и

PQ     P,Q    PQ        PQ 1                                1                   IJPQ                   IJPQ жесткости взаимного влияния BJPq , ВЦрq (ВЦрq = BpQIJ) вычисляются по формулам:

A IJPQ   cel Cell J ^PIJPQ^dV't, ,

^T , V ^cel l

В ⁽²⁾ = ⁸ f E P dV,

B IJPQ   celdl J ^ 3 ^PIJPQ dV ,

^T , V , cell

в ⁽¹⁾ =—

IJPQ v ce

D = Р

IJPQ ce

>. dV ,

-IJPQ dV .

Эти жесткости входят в систему связанных осредненных уравнений равновесия, следующую из (9), (11):

A lJKL v K , LJ B LJKL w, KLJ + ^fl ( x ) ⁰, - ^BJL v K , LlJ + D 1JKL w , KLlJ = P ( x ) .

Поскольку жесткости AlJKL имеют порядок 8, изгибные жесткости — порядок 83, а смешанные — 82, то при асимптотическом анализе целесообразно считать, что p (x) = O(83), а fl = O(82). Тогда можно ввести новые силы, так что p = 83p , f = 82fI, и система (13) примет вид:

A lJKL v K , LJ - ^BlJKL w, KLJ +^ ^f1 = ⁰, - B ljKL v K , LlJ ⁺ DU KIL w , KLlJ = ⁸ p .

При этом v_l = O ( 8 ) , а w = O ( 1 ) . Таким образом, для вычисления жесткостей (12) необходимо решить локальные задачи (6), (7).

Вычисление жесткостей важно для анализа деформируемости гофрированной пластины и, следовательно, эффективности ее применения в различных технических изделиях, например, в барабанах стиральных машин или в качестве элементов кузовов автомобилей.

Далее приводится сравнение жесткостей трех пластин: пластины со смещенными четырехугольными ячейками (Рис. 1, а); пластины с шестиугольными ячейками (сотовой) (Рис. 1, б); пластины, составленной из четырехугольных ячеек (Рис. 1, в). Используемая в работе сотовая пластина (Рис. 1, б) является реальной, изготовленной по специальной технологии, при которой два из шести ребер соты оказываются выпуклыми верх, в то время как оставшиеся четыре ребра выпуклы вниз (они выделены на рисунке 3 жирным линиями). Пластина утрачивает симметрию при любом повороте осей X и Y на 60º. Поэтому эффективные жесткости не изотропны, хотя отклонения ячеек от правильной шестиугольной формы невелики. Для гофрированных пластин небольшое изменение формы приводит к существенным изменениям жесткостей. Две другие пластины (Рис. 1, а, в) являются модельными.

Численное решение задач (6), (7) осуществлено методом конечных элементов (МКЭ), реализованным в виде программы на языке Фортран. Использованы трехмерные изопараметрические элементы с трилинейными функциями формы, называемые элементами Brick [12]. В цель данной статьи не входит детальное описание всех аспектов численной реализации решения, но на тех, которые представляют интерес, следует остановиться.

Решение линейных краевых задач с помощью МКЭ в настоящее время является рутинной процедурой, однако ряд причин, присущих конкретной задаче, может изменить это положение. Так в задачах (6), (7) усложняющими факторами служат малая толщина пластины и наличие периодических условий. Для того чтобы малое значение толщины не приводило к неверным с точки зрения механики результатам — локингу (locking) [13], элементы выбираются с соотношением сторон порядка единицы. Учитывая сложную форму гофрированной пластины, это требование не кажется чрезмерным, а соответствует стремлению обеспечить необходимую точность вычисления всех жесткостей. Число узлов сетки в поперечном направлении колеблется от 2 до 5, вдоль сторон ячейки периодичности — от 30 до 100, что приводит к линейным системам от 14 до 90 тысяч уравнений. Решение системы осуществляется прямым решателем и вполне доступно для компьютера средней мощности. Например, решение всех шести задач (6), (7) занимает 12 минут в случае самой большой сетки на ноутбуке с частотой процессора 1,8 ГГц.

Можно отметить, что решение линейных систем прямым методом весьма эффективно в данном случае вследствие малости числа узлов в поперечном направлении, что приводит к матрице системы с не слишком широкой лентой.

Задачам (6), (7) соответствуют вариационные уравнения:

f CijHN\pQiMrrdV, + f CupQnMrd4 = 0, j ijkl     kPQ, l    i, J    0 j iJPQ Ji 0

cellcell

C  N bkPo I M Tr dVk - f 0₃ CjPo n M p d ^e = 0.

J ijKl kPQ,l i,J 0      3 J iJPQ J i q cellcell

Здесь N eiPQ , N biPQ представляют собой решения, а M ipr пробные функции. И те, и другие принадлежат пространству функций G , являющемуся подпространством W21 , в котором

G = ( f : f _G W 1 , f = f I

I ^{J           2 J} 0a= l a /2      ^J ',, l „/ 2 J

функции удовлетворяют условиям периодичности:

( a = 1,2). При выводе (14) учтены граничные условия (6) и условия периодичности (7). Далее уравнения (14) употребляются стандартным образом [12] в сочетании с методом Галеркина, в котором пространство G аппроксимируется конечномерным подпространством GN кусочно-полиномиальных функций, обладающих периодичностью. Глобальные базисные функции уi, использованные в данной работе, строятся с помощью изопараметрического отображения из трилинейных локальных функций формы стандартного кубического элемента и обладают свойством периодичности. Последнее означает, что если узел i находится на боковой границе 0 = —L/2, то ы-| = V,-| (а = 1,2).

“ “ i q _a = l _о/ 2 i 0 _a =— l 2

В случае ячеек периодичности, обладающих двумя перпендикулярными друг другу плоскостями симметрии, решение локальных задач (6), (7) упрощается. Ячейки именно такой формы используются далее для всех трех типов исследуемых пластин. Итак, рассматривается случай, когда плоскости 0 _lq. и 0 . 0 . являются плоскостями симметрии формы (и упругих свойств, в общем случае). Тогда условия симметрии и периодичности сводятся к краевым условиям на боковой границе. В случае P , Q = 1, 1 или P , Q = 2, 2 на боковой границе выполняются условия равенства нулю нормального перемещения и касательных напряжений. В случае P , Q = 1,2, наоборот, равняются нулю касательные перемещения и нормальное напряжение. Например, при P = Q условия периодичности (7) заменяются условиями

e aPP s =ftn qa ‘a'

= N e

« PP _a =— l a /2    0, C iJkl N kPP , i n J q_a= l a /2

e

C iJkl N kPP , lⁿJ q_a=— l a /2

= 0,

b

N ^{a PP} q_a= i a /2

b a PP f qa

—

b la/2    0,  CiJklN kPP,inj qa= ia/2

b

C iJkl N kPP , l n j q_a=— l a /2

= 0,

( i = 1,2,3, i ^ a ) ,

(по P суммирование не производится).

Другим упрощением решения задач (6), (7) может быть замена искомых функций на новые неизвестные функции вида: M^e _IP Q = N P _e + 1/2 ( q _P 5 _1Q +0 _Q 5 _1P ) , M 3 _P q = N^ee_P Q и M Ipq = N Ipq — 0 з/2 ( 0 P 5 1Q +0 Q 5 1P ) , M 3bPQ = N ^bbPQ + 12 0 p 0 q ■ Вместо (6) функции M ^,

M kbPQ теперь удовлетворяют однородным уравнениям равновесия, а также модифицированным условиям периодичности:

[ M lpQ - (I² ) ( ^ p 5 IQ + _ Q 6 IP ^ 1 . 2 = [ M* PQ - ( 1/2 ) ( ^ p 6 IQ + . Q 6 IP ) ] _।    1 _y 2

M 3 '^pQ| e.- 1 :/2 = M ^epQi,-1 ‘/2 •

[ ^MIpQ + ( 4 з / ² ) ( 4 P ⁶ IQ + 4 Q ⁶ IP ) 1 _,,, = [ M IPQ + 4 з / 2( 4 P ⁶ IQ + 4 Q ⁶ IP )],, . ,_1/2 1 ⁴a 'a/^                                                               ~¹1 ⁴a 'a/^

[ M bPQ -0/ 2 ) 4 P 4 Q ]      =[ M bPQ ( - ) 4 p 4 Q 1. i . ( a =l ² ) .

1 ⁴a 'a                                                      1 ⁴a 'a/^

На свободной границе выполняется обычное условие отсутствия нагрузки:

( C jkl M' kPQ! ) , j = 0, ( C jkl M' kPQ • I ) , j = 0,

^Cijk:l^M kPQ • l n j = 0,    ^Cijk;l^M kPQ , l n j = ⁰¹

В случае двоякосимметричной ячейки периодичности вместо (17) имеют место условия, аналогичные (15). При P = Q они выглядят так:

[ м a ePP -4.L .,,,„= о, I—                    —I ⁴a —‘a'

C ijkl M ^ekPP , l n , _j

I         ^Cijk;l^M kPP , l n j

14a= l a /2

E     ⁴/2     ⁰,

4a    a' ^

[ M a bPP +4 з 4 „ ] , _.,,„

I—                           —I 4a -'a,z-

0, C ijkl M kPP , lⁿj 4 _a = l a /2

= C jkl M^b kPP , l n j

4 a =- 1 a /2     0,

i = 1,2,3, i ^a , a = 1,2.

Задача (17), (18) представляет собой обычную смешанную краевую задачу, стандартно решаемую МКЭ. Случай P ^ Q похож на рассмотренный.

Функции M kePQ имеют ясный механический смысл: это есть флуктуации поля перемещений, возникающие в случае макрооднородной деформации растяжения–сдвига: v, =£°IJxJ, v3 = 0. Тогда перемещения в пределах ячейки периодичности имеют вид: ui =вMeiPQ (4i,42,43 )sPq . Аналогично, MbPQ есть флуктуации поля перемещений, возникающие в случае макрооднородного состояния изгиба и кручения, когда снова в пределах одной ячейки периодичности прогиб составляет w = (12 )к PqXpXq , а перемещения равны ui = вM^q ( 4i • 42 • 43) kPq .

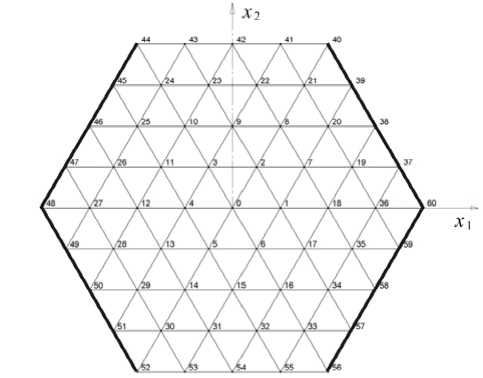
Рис. 3. Элементы грубого разбиения ячейки периодичности сотовой пластины (выделены ребра, выпуклые вниз)

Таблица 1. Координаты узлов элементов грубого разбиения ячейки периодичности сотовой пластины

Номер узла, N	zn , мм	Номер узла, N	zn , мм
0	1,000	21, 24, 30, 33	0,320
1, 2, 3, 4, 5, 6	0,940	22, 23, 31, 32	0,630
7, 11, 13, 17	0,740	27, 36	0,285
8, 10, 14, 16	0,745	37, 39, 45, 47, 49, 51, 57, 59	– 0,170
9, 15	0,875	38, 46, 50, 58	– 0,245
12, 18	0,700	40, 44, 48, 52, 56, 60	0
19, 26, 28, 35	0,310	41, 43, 53, 55	0,220
20, 25, 29, 34	0,300	42, 54	0,315

В разработанной программе вычисления жесткостей возможны два способа задания формы пластины. В первом способе значения координаты z узлов грубой сетки (Рис. 1, Рис. 3) вводятся в программу вместе с прочими данными, во втором — берутся из файла координат z узлов мелкой сетки. При втором способе форма пластины моделируется более точно. В качестве примера в Таблице 1 приводятся координаты z узлов элементов грубой сетки для сотовой пластины, показанной на рисунке 3.

Конечно-элементная сетка, на которой решаются локальные задачи, является более мелкой, чем сетка, используемая для пластины в целом. Например, для ячейки периодичности сотовой пластины вычисления проводятся на прямоугольной сетке, показанной на рисунке 2. При этом координаты узлов мелкой сетки (уже прямоугольной) получаются интерполяцией данных грубой сетки.

Поскольку для всех исследуемых пластин плоскости ^3 и ^ 2 ^ 3 являются плоскостями симметрии, уравнения (11) приобретают более простой вид:

(1)                  Z?(1)

^1N11   ^1111 ^e 11 ⁺ ^1122 ^e 22 + ^и 1111 ^к 11 + ^и 1122 ^к 22 ,

^N 22    A 2211 e 11 ⁺ A 2222 e 22 ^{+ B} ^2211 ^К 11 ^{+ B} ^2222 ^К 22 ,

М = В ⁽²⁾ е + 5(²) D к + D к ^1V111   ° 1111 ^e 11 + ^и 1122 e 22 ⁺ ^1111 ^ 11 ⁺ ^1122 ^к 22 ,

М  =в ⁽²⁾   е -В' ²⁾   е к + D к

1V1 22        2211 ^e 11 + °  2222e 22 ⁺ ^2211 ^к 11 ⁺ "^2222 ^к 22 ,

N 4 Р ■ R ⁽¹⁾    W

1N 12   ^1212 ^e 12 + ^ 1212 ^к 12 ,

м =В ⁽²⁾   е к

^1И 12        1221 ^e 12 ⁺ ^1212 ^к 12 ,

то есть уравнения для растяжения–изгиба (первые четыре выражения) можно решать независимо от уравнений сдвига–кручения (пятое и шестое выражения).

Для верификации авторской программы использовалась коммерческая конечноэлементная программа (ККЭП). Для сравнения в Таблице 2 приведены некоторые результаты вычислений жесткостей на одинаковых, состоящих из однотипных элементов типа Brick сетках с количеством узлов 60×40×5. Отношение толщины листа h к стороне ячейки периодичности l ₁ принято равным 0,0236. Из Таблицы 2 следует,

Таблица 2. Результаты вычислений авторов и с помощью ККЭП (для наглядности компоненты жесткостей записаны в формате матрицы)

A1111 A1122 B11111 B11122 Авторская программа 1,44∙10–2 1,03∙10–3 5,58∙10–5 6,51∙10–5 ККЭП 1,44∙10—2 1,02∙10–3 5,50∙10–5 6,50∙10–5 A2211 A2222 B12211 B12222 Авторская программа 1,05∙10–3 5,52∙10–3 -1,80∙10–6 2,79∙10–5 ККЭП 1,02∙10–3 5,60∙10–3 -1,00∙10–6 2,60∙10–5 что значения жесткостей отличаются друг от друга почти на три порядка. Поэтому их вычисление с принятой в инженерных расчетах точностью 5% представляет сложную задачу и требует использования мелкой сетки. Хорошее совпадение жесткостей, найденных с помощью разных программ, говорит о достоверности результатов.

С использованием разработанной программы исследована зависимость жесткостей от параметров пластины: толщины листа h , высоты пластины f (см. Рис. 1) и выбора координаты отсчетной плоскости z ref . На представленных графиках значения жесткостей A_iijj , B_iijj , D_iijj отнесены к соответствующей максимальной жесткости. Величины h , f и z ref также являются безразмерными (каждый параметр нормирован по своему максимальному значению). Знак тильды в дальнейшем опущен. Зависимости A ₁₁₁₁, A ₂₂₂₂, A ₁₁₂₂ показаны на рисунках 4, 5.

Наблюдается монотонная зависимость жесткостей от толщины пластины. При этом графики на рисунке 4 показывают, что никакая пластина не имеет по жесткости однозначного преимущества. Действительно, если наибольшее значение компоненты A 1111 характерно для сотовой пластины, то наибольшее значение компоненты A 2222 достигается у четырехугольной симметричной пластины. На рисунке 5 хорошо видно, что продольные жесткости A 1111 и A 2222 у сотовой пластины не равны вследствие имеющей место несимметрии ее формы.

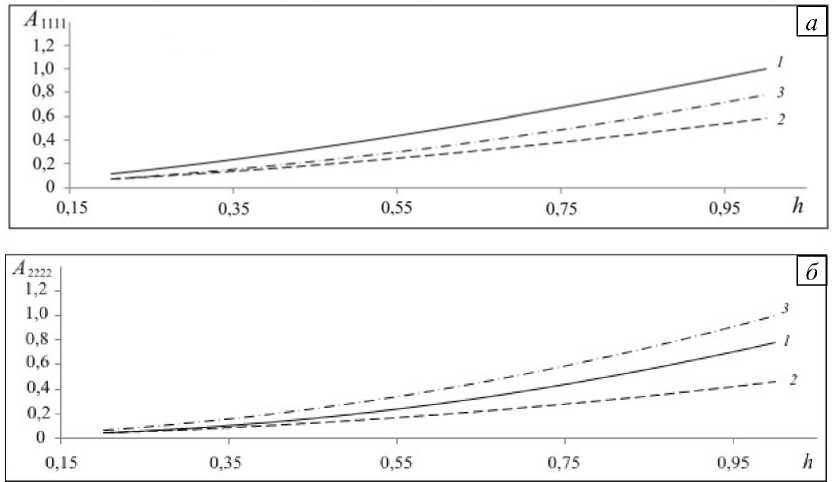
Рис. 4. Компоненты жесткости A ₁₁₁₁ ( а ) и A ₂₂₂₂ ( б ) для пластин различного типа: сотовая пластина (кривая 1 ), пластина со смещенной четырехугольной ячейкой ( 2 ), пластина с четырехугольной ячейкой ( 3 )

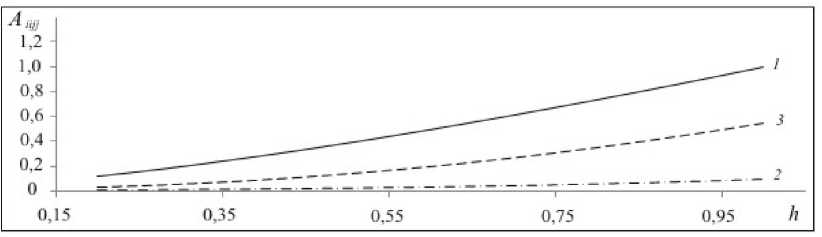
Рис. 5. Зависимость жесткостей сотовой пластины от толщины листа: A ₁₁₁₁ (кривая 1 ), A ₁₁₂₂ ( 2 ), A ₂₂₂₂ ( 3 )

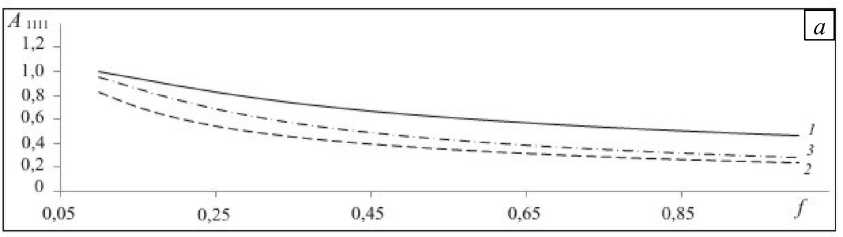
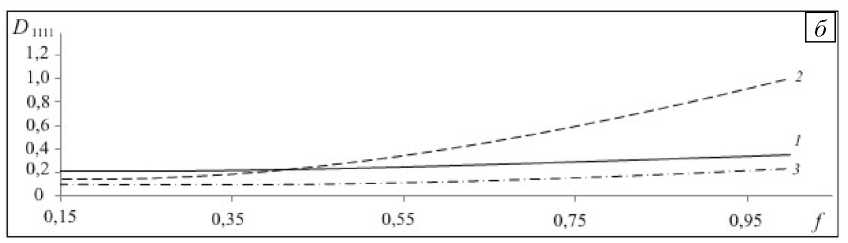
Рис. 6. Влияние толщины пластины на продольную A1111 (а) и изгибную D1111 (б) жесткости у пластин различного типа: сотовая пластина (кривая 1), пластина со смещенной четырехугольной ячейкой (2), пластина с четырехугольной ячейкой (3)

В «я ~-^_        1,0" - 0,30_____0.10 ^	-—_^0Л0          0,30          0.50           0,70          0.90      2
---------L---о -0,5 -1,0 -1.5 -2.0 -2.5-	4

Рис. 7. Зависимость значения компонент B_iijj матрицы жесткости сотовой пластины от положения отсчетной плоскости: B ₁₁₁₁ (кривая 1 ), B ₁₁₂₂ ( 2 ), B ₂₂₁₁ ( 3 ), B ₂₂₂₂ ( 4 )

Рисунок 6 содержит зависимости жесткостей пластин от высоты f . На графиках видно, что при малых f значение жесткости A ₁₁₁₁ быстро убывает с ростом высоты, а при f, больших 0,45^0,5, падение жесткости замедляется и изменения могут оказаться несущественными. При тех же значениях f изгибная жесткость D ₁₁₁₁ резко растет для пластины типа 2 , поэтому за счет продольной жесткости можно получить существенный выигрыш в изгибной жесткости. Это подтверждает необходимость проведения детального анализа жесткостей каждой пластины.

Авторами также изучена зависимость жесткостей от координаты Z , указывающей местоположение плоскости отсчета z ref относительно плана пластины. При z ref = 0 в отсчетной плоскости находятся узлы 40, 44, 48, 52, 56, 60 (см. Таблицу 1). Положение этой плоскости больше всего сказывается на жесткостях взаимного влияния. Значение z ref варьировалось в экспериментах от - 0,25 до 1 мм. Из графиков, представленных на рисунке 7, видно, что существует такое положение отсчетной плоскости, когда все жесткости взаимного влияния B iijj близки к нулю. В этом случае при расчете параметров деформирования уравнения растяжения и изгиба можно решать независимо.

Подводя итог проведенным исследованиям, следует отметить, что в силу существенной анизотропии каждая из пластин рассмотренных типов обладает преимуществом по отдельным жесткостям, но не в целом. Таким образом, у любой конкретной пластины необходимо производить расчет всех жесткостей, так как достаточно сложно обнаружить какую-либо простую закономерность в их зависимости от параметров пластины.

Авторы благодарны профессорам Ф. Мирчу и А. Дуде из Технического университета Берлина за инициирование данной работы и предоставление данных.