Эффективный радиус нагрева E-слоя ионосферы мощным КВ-излучением

Существующие установки, такие как «Сура» в России, «Тромсё» в Норвегии и HAARP в США, могут обеспечивать нагрев электронов ионосферной плазмы мощным радиоизлучением КВ-диапазона [Гуревич, 2007]. Если это излучение направлено вертикально вверх в пределах телесного угла 2ξ, то на фиксированной высоте z оно имеет вид пятна радиусом a [Gurevich, 1978]:

E ²= E m ²exp(- r ²/ a ²), (1) где E m – амплитуда электрического поля радиоволны на частоте ω в центре пятна на этой высоте, r – горизонтальное расстояние, отсчитываемое от этого центра, a = z tgξ – характерный радиус пятна излучения (т. е. радиус засветки ионосферы радиоизлучением на данной высоте). На высотах области E ионосферы (100–150 км) и ниже этой области эффективность нагрева электронов электрическим полем радиоволны в значительной степени определяется долей энергии δ e , теряемой электронами при упругих и неупругих столкновениях с нейтральными частицами [Гуревич, Шварцбург, 1973; Гуревич и др., 1975; Gurevich, 1978; Kotik, Itkina, 1998]. Величина δ e зависит от температуры электронов T e , что приводит к нелинейной зависимости T e от E ² [Гуревич, Шварцбург, 1973; Гуревич и др., 1975; Gurevich, 1978]. Возможно, что эта же нелинейная зависимость приводит к существенному отклонению радиального распределения T e от E ², когда эффективный радиус нагрева ионосферы r eff отчетливо отличается от характерного радиуса пятна излучения a . Проверка этого предположения для высот области E ионосферы на основе теоретических оценок была главной целью данной работы.

Постановка задачи

Пусть мощное радиоизлучение КВ-диапазона наземной установки – единственный источник нагрева электронов на высотах области E ионосферы. Во многих случаях такое предположение оправданно, поскольку для фоновых условий на высотах области E обычно Te0=Tn, где Te0 – температура электронов для фоновых условий, Tn – температура нейтральных частиц [Гуревич, Шварцбург, 1973; Gurevich, 1978]. На этих высотах частота упругих столкновений электронов определяется в основном столкновениями электронов с нейтральными частицами, (νe≈νen), и для типичного диапазона частот ω мощного КВ-радиоизлучения (3–10 МГц) обычно выполнено условие ω2>>νеn2 [Гуревич, Шварцбург, 1973; Gurevich, 1978]. Кроме того, пусть фиксированная частота ω2>>ωpe2, где ωpe – плазменная (ленгмюровская) частота электронов, т. е. эффекты, связанные с резонансным нагревом электронов на высотах области E [Гуревич, Шварцбург, 1973; Gurevich, 1978; Frolov et al., 2002], несущественны. В этом случае для стационарных условий [Гинзбург, Гуревич, 1960]

δ T e =( T e - T n )/ T n =(δ e0 /δ e )( E ²/ E p ²), (2)

Ep=ω(3kTnδe0m/e2)1/2, где δe0 – доля энергии, теряемая электронами для фоновых условий, т. е. δe0=δe при Te=Te0=Tn, E – электрическое поле радиоволны на частоте ω, которое определено уравнением (1), Ep – характерное плазменное поле, k – постоянная Больцмана, m и e – масса и заряд электрона.

На высотах области E величина δe определяется в основном упругими и неупругими столкновениями электронов с нейтральными частицами (O, N2 и O2) [Гуревич, Шварцбург, 1973; Gurevich, 1978]. Эти процессы учтены с помощью приведенных в монографии [Schunk, Nagy, 2009] формул для вычисления скоростей охлаждения электронов при их упругих столкновениях с O, N2 и O2, возбуждении тонкой структуры O(3P) и уровня O(1D), возбуждении вращательных и колебательных уровней N2 и O2. Отметим, что используемая здесь скорость охлаждения электронов при возбуждении вращательных уровней O2 [Pavlov, 1998а] в 13 раз меньше приве- денной в [Dalgarno, 1969]. Скорость охлаждения электронов из-за возбуждения колебательных уровней N2 [Pavlov, 1998b] отличается от широко используемой [Stubbe, Varnum, 1972] в пределах фактора 0.6–2.0 в зависимости от Te. Скорости охлаждения электронов при упругих столкновениях электронов с O, N2 и O2 являются общепринятыми [Кринберг, Тащилин, 1984; Брюнелли, Намгаладзе, 1988].

Для вычисления параметров термосферы использована модель [Picone et al., 2002]. На высотах области E эти параметры зависят от гелиогеофизиче-ских условий гораздо слабее, чем на больших высотах [Picone et al., 2002]. Тем не менее, для определенности эти условия зафиксированы: равноденствие (90-й день года), средний уровень солнечной активности (величина потока радиоизлучения Солнца на длине волны 10.7 см в 10 - 22 Вт/(м 2 Гц) - индекс F 10.7 =130), низкий уровень геомагнитной активности (планетарный индекс этой активности A p =4 нТл), полночь, географические координаты соответствуют установке «Сура» (56.13° N, 44.1° E), высота h =110 км. В этом случае T _е0= T n =231 K, 8_е0=4.1 10 - ³ и, например, для частоты f = to/2п=4 МГц характерное плазменное поле E p ~1 В/м. На рис. 1 приведена зависимость 8_е от T _е в относительных единицах для заданных гелиогеофизических условий. Видно, что 8_е уменьшается с ростом T _е, достигает минимального значения 8_е~0.18_е0 при 8 T _е~5^6 и увеличивается с ростом T _е при 8 T _е>6. Это в значительной степени связано с важным влиянием потерь энергии электронов на возбуждение вращательных и колебательных уровней N 2 для относительно низких и высоких значений T e соответственно. Отметим, что существование минимума в зависимости 8 e от T e - известное свойство области E и нижней ионосферы [Гуревич, Шварцбург, 1973; Гуревич и др., 1975; Gurevich, 1978; Kotik, Itkina, 1998].

Уравнение (2) с учетом приведенной на рис. 1 зависимости 8 e от T e является нелинейным уравнением для T e при заданном электрическом поле радиоволны (1), решение которого позволяет определить искомое радиальное распределение T _e на заданной высоте в области излучения мощной радиоволны. Ниже приведены результаты анализа решения уравнения (2) для заданных условий.

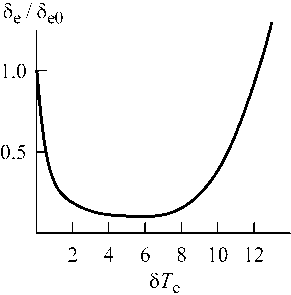
Рис . 1. Зависимость доли теряемой электронами энергии 8_е на высоте 110 км от температуры электронов T _е (относительные единицы).

Результаты анализа

Анализ показал, что характер радиального распределения T e зависит от амплитуды электрического поля радиоволны E m при заданном (гауссовом) радиальном распределении этого поля (1): при E m < E p зависимость T e от r слабо отличается от гауссова распределения, но эффективный радиус этого распределения r eff меньше характерного радиуса излучения a ; при E _m> E _p зависимость T _e от r существенно отличается от гауссова распределения, и r _eff> a (рис. 2). Это связано с нелинейной зависимостью 8_е от T _е (рис. 1). Для E m < E p значения 8_е попадают в область уменьшения 8_е с ростом T _е, поэтому 8_е увеличивается при переходе от центра к периферии области нагрева. Это приводит к более высокому темпу уменьшения T e c радиальным расстоянием и тем самым обеспечивает выполнение условия r eff < a . Для E _m/ E _p>1 значения 8_e попадают в область увеличения 8_e с ростом T _e в центральной части нагрева и в область уменьшения 8_е с ростом T _е в периферийной части нагрева, которая соответствует r > a . В результате в центральной части нагрева зависимость T e от r ослаблена, а при переходе к периферийной части нагрева происходит очень быстрое, почти ступенчатоподобное уменьшение T e . Поэтому эффективный радиус нагрева ионосферы r eff определен как радиус, который примерно соответствует середине этого ступенчатоподобного уменьшения T e . Из приведенных оценок можно видеть, что в обоих случаях на r = r _eff характерный масштаб изменения T _e с радиальным расстоянием меньше масштаба изменения квадрата электрического поля радиоволны E ², поскольку на r = r _eff величина 8_e уменьшается с ростом T e как для низкой, так и для высокой амплитуды электрического поля радиоволны E m . Следует отметить, что условие E m / E p >1 может быть выполнено для области E ионосферы только в исключительных случаях из-за сильного поглощения радиоволн в нижней ионосфере [Kotik, Itkina, 1998]. Поэтому вывод об относительно малом радиальном масштабе T e на r = r eff почти независимо от амплитуды электрического поля представляет особый интерес.

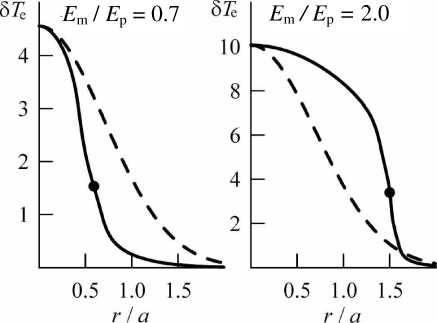
Рис 2 . Радиальные распределения температуры электронов T _e в относительных единицах для двух значений E _m/ E _p, вычисленные по уравнению (2) – сплошные линии; для варианта гауссова радиального распределения T _e с характерным радиусом a – штриховые линии. Точки соответствуют r = r _eff.

Зависимость r eff от электрического поля радиоволны более детально представлена на рис. 3. Из рисунка видно, что температура электронов T em в центре пятна излучения, т. е. при r =0 на заданной высоте, увеличивается с ростом E m , и скорость этого увеличения максимальна в интервале E m / E p ≈0.6÷0.7. В конце этого интервала достигается минимум r _eff, и область этого минимума связана с минимумом в зависимости δ_e от T _e (см. рис. 1), точнее, соответствует началу увеличения δ e с ростом T e . При E _m/ E _p>0.7 происходит увеличение r _eff, и скорость этого увеличения уменьшается с ростом E m из-за соответствующего увеличения δ_e (см. рис. 1).

Изменения концентрации электронов n e на высотах области E при нагреве ионосферы мощной радиоволной связаны в основном с увеличением T e в области нагрева из-за зависимости коэффициента диссоциативной рекомбинации электронов α от T e [Гуревич, Шварцбург, 1973; Gurevich, 1978]. Величина α различна для ионов в основном (α 0 ) и колебательно возбужденном (α v ) состояниях [Sheehan, St.-Maurice, 2004]. Для качественных оценок α в интервале T e =300÷4000 K можно принять, что

α=(1– T e /4000)α 0 +( T e /4000) α v .

С учетом явного вида α 0 и α v [Sheehan, St.-Maurice, 2004] и преобладания NO⁺ в ионном составе на рассматриваемых высотах это соотношение можно представить в виде

α≈3.3 10^–13(300/ T e ), м²/с. (3)

Зависимость α∼ 1/ T e использована во многих работах по анализу изменений в ионосфере, связанных с нагревом ионосферы мощными радиоволнами [Гуревич, Шварцбург, 1973; Gurevich, 1978]. Уравнение (3) – качественное обоснование справедливости этой зависимости. Относительные изменения n e из-за нагрева E-слоя ионосферы мощной радиоволной (с учетом (3)) можно представить в виде [Гуревич, Шварцбург, 1973; Gurevich, 1978]

δ n e =( n e – n e0 )/ n e0 =( T e / T e0 )^1/2-1, (4)

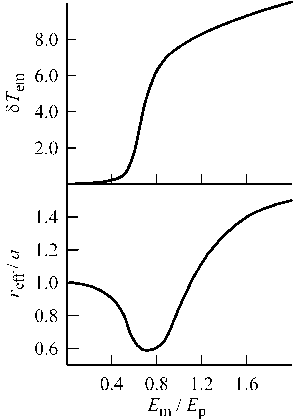
Рис . 3 . Зависимость температуры электронов в центре пятна излучения, где r =0 и T _e= T _em, и эффективного радиуса нагрева ионосферы r _eff на высоте 110 км от амплитуды электрического поля радиоволны E _m (относительные единицы).

где индекс 0 соответствует фоновым условиям. На рис. 4 приведены результаты вычисления δ n _e по известным δ T _e для заданных условий. Из рис . 2 и 4 видно, что радиальные распределения δ T _e и δ n _e качественно подобны. Эффективный радиус нагрева ионосферы r _eff, определенный по данным δ T _e, применим и для δ n _e. Например, для E _m> E _p эффективный радиус r eff примерно соответствует середине ступенчатоподобного уменьшения как δ T _e, так и δ n _e.

Относительно сильный градиент T e и n e на границе области нагрева ( r = r eff ) может приводить к генерации продольных токов и плазменных неустойчивостей на этой границе. Поэтому экспериментальное исследование характера радиального распределения T e и n e в области нагрева ионосферы мощными КВ-радиоволнами представляет определенный интерес.

Обсуждение

Приведенные результаты анализа показали, что характер радиального распределения температуры T e и концентрации n e электронов в области нагрева E-слоя ионосферы мощным КВ-излучением в значительной степени определяется зависимостью доли энергии δ e от T e . Использованная для анализа зависимость δ e от T e получена на основе современных суммированных в монографии [Schunk, Nagy, 2009] знаний о скоростях охлаждения электронов при упругих и неупругих столкновениях электронов с нейтральными частицами. Выше отмечалось, что некоторые из этих скоростей существенно отличаются от широко использованных ранее: скорость охлаждения электронов при возбуждении вращательных уровней O₂ в 13 раз меньше приведенной в [Dal-garno, 1969], скорость охлаждения электронов из-за возбуждения колебательных уровней N 2 отличается от приведенной в [Stubbe, Varnum, 1972] в пределах фактора 0.6–2.0 в зависимости от T e . Для оценки важности этих отличий обозначим через (δ e ) old долю теряемой электронами энергии, для вычисления которой, в отличие от δ e , используются приведенные в [Dalgarno, 1969; Stubbe, Varnum, 1972] скорости охлаждения электронов при возбуждении вращательных

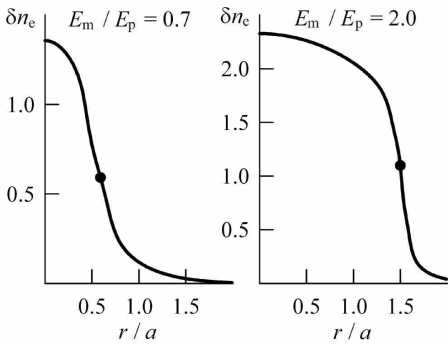
Рис 4. Радиальные распределения концентрации электронов n _e в относительных единицах, вычисленные по формуле (4) для двух значений E _m/ E _p. Точки соответствуют r = r eff .

уровней O₂ и колебательных уровней N₂. Для фиксированных гелиогеофизических условий, которые определены выше (равноденствие, средний уровень солнечной и низкий уровень геомагнитной активности, географические координаты соответствуют установке «Сура», полночь, высота 110 км), получим, что для фоновых условий T e0 = T n =231 K, δ e0 =4.1·10 ^{- 3}, (δ e0 ) old =4.6·10 ^{- 3}. Отличие (δ e0 ) old от δ e0 почти целиком связано с использованием разных скоростей охлаждения электронов при возбуждении вращательных уровней O 2 , и увеличение этой скорости в 13 раз привело к очень слабому увеличению доли энергии, теряемой электронами: (δ e0 ) old /δ e0 =1.12. Это связано с тем, что скорость охлаждения электронов при возбуждении вращательных уровней N 2 больше соответствующей скорости для O₂ как для современных, так и для использованных ранее значений скоростей этих процессов. Дополнительный анализ показал, что отличие (δ_e)_old от δ_e становится существенным только для T e / T n >8, когда возбуждение колебательных уровней N 2 становится основным процессом охлаждения электронов при неупругих столкновениях электронов с нейтральными частицами. В данном случае δ e /(δ e ) old ≈1.7 и 2.0 при T e / T n =10 и 12. Следовательно, современные скорости охлаждения электронов приводят к более высоким значениям δ e для T e / T n >8 и тем самым накладывают более жесткие ограничения на увеличение T e с ростом мощности КВ-излучения по сравнению с использованными ранее значениями этих скоростей. В остальном качественный характер зависимости (δ e ) old от T e не отличается от приведенного на рис. 1 для δ e . Поэтому замена δ e на (δ e ) old не приведет к изменению качественных результатов анализа, и только при T _e/ T _n>8 количественные результаты будут существенно отличаться.

Выводы

Приведенные результаты теоретического анализа радиального распределения температуры T e и концентрации n e электронов в области нагрева ионосферы мощным КВ-радиоизлучением на высотах E-слоя позволяют сделать следующие выводы.

• 1.    Эффективный радиус этого нагрева r eff меньше характерного радиуса пятна излучения a , когда амплитуда электрического поля в центре пятна E m меньше характерного плазменного поля E _p и r _eff> a для E _m/ E _p>1. Это связано с нелинейной зависимостью доли энергии, теряемой электронами, от T e .

• 2.    На границе области нагрева ( r = r eff ) характерный радиальный масштаб изменения T e меньше соответствующего масштаба изменения квадрата электрического поля излучения, т. е. на этой границе формируется относительно сильный градиент n e и T e как для E m < E p , так и для E m > E p .

• 3.    Этот градиент увеличен для E m > E p , когда на границе области нагрева происходит ступенчатоподобное уменьшение T _e и n _e.