Эйлеров метод моделирования дисперсных систем на примере полимеразной цепной реакции

RUSSIAN JOURNAL OF BIOMECHANICS

Как известно, в механике различают два подхода к описанию движения сплошной среды: методы Эйлера и Лагранжа. В первом случае рассматривают временную зависимость переменных, описывающих состояние среды для каждой фиксированной точки пространства в некоторой системе отсчёта. Во втором случае наблюдают за частицами сплошной среды, которые перемещаются по пространству [1].

При моделировании динамики многофазных сред возникает задача описания каждой из сред. Если речь идет о дисперсной среде, то несущая фаза, как правило, описывается с помощью метода Эйлера. А вот описание дисперсной фазы зависит от её свойств. Здесь также можно выделить два подхода. Модель Эйлера – Эйлера (ЭЭ) исходит из предположения, что дисперсная фаза, точно так же, как и сама дисперсионная среда, описываются с использованием уравнений в Эйлеровом представлении. С другой стороны, модель Эйлера – Лагранжа (ЭЛ) предполагает, что уравнения динамики среды записываются в рамках описания Эйлера, а частицы дисперсной фазы описываются на основе дискретной механики, т.е. в рамках метода Лагранжа.

Каждый из подходов имеет свои достоинства и недостатки. Преимущество ЭЛ метода заключается в том, что мы можем отслеживать траекторию отдельных частиц, их взаимодействие, изменения размеров каждой частицы и т.д. Однако, с другой стороны, такое

0000-0002-0756-4795

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

моделирование требует значительных вычислительных ресурсов, тем больших, чем больший масштаб модели необходимо описывать. В случае ЭЭ описания, дисперсная фаза описывается на основе уравнений неразрывной среды с введёнными дополнительными ограничениями. Такой подход в значительной степени упрощает вычислительный процесс, но при этом и ограничивает в возможностях моделирования изменений отдельных частиц в рамках дисперсной среды. Конечное решение, какой способ описания использовать, исследователь должен принимать, основываясь на свойствах дисперсной фазы и мощности вычислительной техники, которая имеется в его распоряжении.

Одним из преимуществ многофазных моделей при работе с дисперсными средами является возможность сравнительно просто и корректно учесть физические механизмы, приводящие к появлению относительной скорости между дисперсными частицами и базовой жидкостью. К таким механизмам можно отнести инерцию,  броуновскую  диффузию, термофорез, диффузиофорез, эффект Магнуса, дренаж жидкости и гравитацию. Очевидно, что ситуации, в которых дисперсные частицы движутся иначе, чем растворитель, представляют особый интерес для многофазных моделей (не важно в каком описании, ЭЭ или ЭЛ), поскольку они имеют преимущества в их описании по сравнению с однофазным подходом. Авторы [2] пришли к выводу, что из различных механизмов воздействия на частицы размером менее 1 микрона, только броуновская диффузия и термофорез являются значимыми. Идея использования моделей ЭЭ и ЭЛ для дисперсионных сред с субмикронными частицами нашла широкое применение. Например, в работах [3; 4] разработаны вычислительные подходы к моделированию многофазного теплообмена и течения жидкости в контурах естественной циркуляции с использованием наножидкостей. Результаты работ свидетельствуют о заметном вкладе термофореза и броуновской диффузии.

Иной подход к моделированию наблюдается при математическом и численном описании полимеразной цепной реакции (ПЦР) – метода, используемого для амплификации нескольких копий ДНК до достаточного уровня концентрации для последующих манипуляций [5]. Эта методика 30 лет назад произвела революцию при изучении генетических паттернов и идентификации организмов, а её изобретатель заслуженно получил Нобелевскую премию 1993 года. Она является основной «рабочей лошадкой» при проведении исследований в области генной регуляции и синтетической биологии [6]. Также метод нашел широкое применение в биомедицинских тестах, криминалистической экспертизе и молекулярной археологии [7–9]. В типичном судебно-медицинском исследовании небольшое количество образца, содержащего ДНК, отбирается на месте преступления, амплифицируется с помощью метода ПЦР, а затем используется для идентификации подозреваемого.

Стандартный термоциклер (оборудование для амплификации ДНК) настроен на проведение трёх характерных реакций единоготемпературного цикла: денатурацию имеющихся молекул ДНК (95–97°C), так называемый отжиг (50–60°C) и, наконец, удлинение участков ДНК (72–77°C). На этапе денатурации двухцепочечная ДНК (здесь и далее для удобства дальнейшей записи уравнений будем обозначать её как dsDNA ) разделяется на две одноцепочечные ДНК ( ssDNA ) под воздействием более высокой температуры. Этап отжига позволяет праймерам оставаться охлажденными и связываться с концами ssDNA . На этапе удлинения отожженная ДНК ( aDNA ) нагревается до 72–77°C, при этом фермент максимально усиливает синтез ДНК; затем из aDNA образуются две новые двухцепочечные ДНК. В результате повторяющегося термического процесса образуется множество копий ДНК-матриц с экспоненциальной скоростью роста. Как видно, реакция имеет разные стадии, каждая из которых требует свои температурные условия.

В настоящее время наблюдается устойчивый рост спроса на недорогие, надежные и портативные системы ПЦР для применения в «полевых» условиях. Именно для таких условий было предложено остроумное решение в виде конвективной ПЦР. Это методика амплификации ДНК использует естественную конвекцию между различно нагретыми поверхностями капиллярной трубки [10]. Для перемещения жидкости через зону с разной температурой не требуется дополнительные усилия, так как в неоднородно нагретой трубке в поле тяжести возникает естественная конвекция. Благодаря простоте конструкции, относительно низкой стоимости её изготовления и более высокой скорости переноса молекул через зоны нагрева, конвективная ПЦР стала популярной, поскольку эта технология позволяет ускорить проведение реакции ПЦР, а также уменьшить размеры амплификатора до характерных размеров микрореактора. Это привело к появлению портативных установок для оперативного проведения ПЦР за пределами лабораторий.

Важную роль в развитии технологии конвективной ПЦР играет численное моделирование, так как измерение любых концентрационных полей в эксперименте, как известно, сталкивается с большими трудностями. Математические модели, разработанные для анализа конвективной ПЦР [11–14], традиционно предполагают, что раствор ДНК является истинным раствором. Поэтому за основу обычно берётся однофазная модель, в которой молекулы ДНК и растворителя движутся одинаково и описываются одним уравнением Навье – Стокса. Эта модель дополняется уравнением реакции-диффузии-конвекции для описания концентраций молекул ДНК на трех стадиях реакции ПЦР.

Такой подход, несмотря на определенные успехи, имеет и некоторые недостатки. Раствор молекул ДНК обладает дуализмом свойств. Обычно он проявляет свойства истинных растворов, но иногда может вести себя как дисперсная фаза. Дело в том, что ДНК представляет собой достаточно сложную молекулу. Если характерный размер нити ДНК в поперечном направлении 2 нм, то сама последовательность очень длинная. Как известно, геном человека, хранящийся в ядре каждой клетки, достигает 2 м в длину при полном распутывании молекулы! Поэтому ДНК имеет несколько уровней упаковки. В наиболее компактном состоянии в форме хромосомы молекула представляет собой объект с характерным размером до 10 мк. А это на порядок превышает характерный размер молекул, рассматриваемых для истинного раствора [2]. На самом деле ситуация ещё сложнее. Амплификация применяется не к полной ДНК, а к её обрывкам разной длины, которые, как правило, уже не имеют компактной упаковки. Поэтому вполне можно привести примеры ситуаций, при котором возможна сепарация молекул ДНК от растворителя: вращение раствора в неподвижном сосуде, действие электрического поля. Традиционно используемая при моделировании реакции ПЦР однофазная модель либо не подходит для описания таких ситуаций, либо требует значительного усложнения. Кроме того, на ход реакции должны оказывать такие механизмы, оказывающие воздействие на движение дисперсных частиц, как броуновская диффузия и термофорез. Однако в существующих работах по моделированию PCR эти механизмы до сих пор не учитывались.

Так как молекула ДНК проявляется себя на разных пространственных масштабах, то моделирование её свойств привлекает совершенно разные методики исследования. Например, микроскопическая механика самой молекулы моделировалась в [15; 16], динамика ансамблей мономеров и димеров в процессах генной регуляции изучалась в [17; 18], образование структур в белковых полях рассматривалось в [18].

Задачей настоящей работы является разработка и апробация математической и численной моделей конвективной ПЦР на основе ЭЭ-описания многофазной жидкой среды, а также проведение сравнения с результатами моделирования в рамках традиционного подхода однофазной среды.

Математическая модель

Рассмотрим конвективную ячейку в форме параллелепипеда, в которой происходит реакция ПЦР (рис. 1). Ячейка имеет ширину l = 2 мм, отношение высоты к ширине у > 1 и отношение толщины к ширине 5 << 1. Таким образом, конфигурация системы попадает в класс ячеек Хеле - Шоу. Под этим понимается гидродинамическая система, помещенная в кювету, у которой толщину зазора по одному из направлений можно признать бесконечно малой по сравнению с другими характерными размерами кюветы. Это имеет три важных следствия для моделирования. С одной стороны, такое допущение позволяет считать наблюдаемые в ячейке Хеле - Шоу потоки двумерными, что упрощает вычисления. С другой стороны, близко расположенные широкие стенки ячейки приводят к возникновению в вязкой жидкости силы сопротивления из-за трения о них. В предельном случае течение вообще может рассматриваться в безынерционном приближении (используется закон Дарси). Если же зазор мал, но сравним по порядку величины с шириной кюветы, то применяют компромиссный вариант, когда в уравнении движения учитывается как слагаемое диффузии скорости, так и сила сопротивления (приближение Хеле - Шоу). Наконец, подобранная конфигурация кюветы обеспечивает стационарный характер конвекции при заданной разнице температур. Необходимо учитывать, что тепловые режимы реакции ПЦР диктуют разность температур, используемую в кювете. Таким образом, единственный параметр, который исследователь может регулировать в этой системе, - это пространственные размеры кюветы. Наиболее важна здесь высота γl, так как число Рэлея, определяющее наступление конвекции, зависит от высоты как ~(y l)3 При высоком амплификаторе система вполне может быстро войти в режим нестационарной конвекции со сложным поведения течения, что нежелательно для эффективного прохождения ПЦР. При меньшей высоте кюветы естественная конвекция вообще может не развиться, так как характерное значение числа Рэлея будет ниже критического значения.

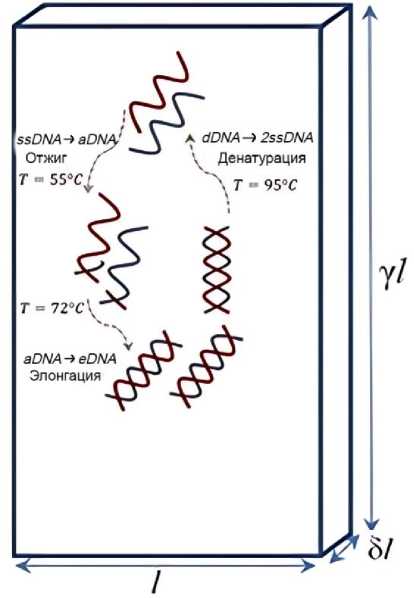
Рис. 1. Схема ПЦР в конвективной ячейке Хеле - Шоу

Пусть нижняя граница ячейки поддерживается при температуре денатурации T H = 95°С, в то время как верхняя грань имеет более холодную температуру отжига T_C = 55°С. Будем считать боковые стенки ячейки теплоизолированными для большей стабильности тепловых условий, поддерживаемых внутри кюветы, а также для экономии тепловой энергии, которая подаётся внутрь. Кювета ориентирована таким образом, чтобы сила тяжести была направлена вдоль наибольшего размера параллелепипеда в сторону более холодной границы. Это гарантирует поддержание в кювете естественной стационарной конвекции.

Ячейку заполняет раствор молекул ДНК трёх видов: ssDNA, dsDNA и aDNA , между которыми идет реакция ПЦР (Рис. 1). Физические свойства растворителя будем считать совпадающими со свойствами чистой воды: плотность ρ w , коэффициент теплопроводности к, коэффициент динамической вязкости ц w .

Для изучения динамических свойств конвективной ПЦР будем использовать ЭЭ-описание. В рамках этой модели трем фракциям молекул ДНК соответствуют три различные дисперсные фазы частиц, а растворитель представляет собой четвертую несущую фазу. Все четыре фазы имеют континуальный характер и для них необходимо записать уравнения неразрывности, переноса импульса и энергии. Так как в системе протекают химические реакции, которые сопровождаются переходами одним компонент в другие, для учета этих реакций в уравнения неразрывности фаз необходимо включить условие межфазного переноса вещества. Уравнения неразрывности для всех фаз имеют вид:

^ (QJV ) ^{+ v} ' ( Q..P„^u J S а . ⁽¹⁾ где и _а, ф_а, р_а - скорость, объемная доля и плотность фазы а; S_a - источник вещества фазы а. Индекс а принимает четыре значения, для которых введем обозначения: а = { w , dsDNA, ssDNA, aDNA }, которые соответственно указывают на растворитель и три дисперсные фазы. Последние будем обозначать индексом p . Следует подчеркнуть, что в отличие от истинных растворов, где содержание растворенного вещества описывается молярной концентрацией, для многофазной среды содержание фазы описывается объемной долей ф_а. Перепишем уравнения неразрывности (1) для молекулярных фаз, отделив диффузионные потоки частиц относительно базовой жидкости j _p от потоков вещества, связанных с реакциями ПЦР S_a:

+ ’■ ( u p ф Р ) = 1е l -’- i p^+Sp ) . (2) t ^Р p

Предположим, что j p является суммой только двух эффектов, связанных с диффузионными процессами: броуновской диффузии и термофореза:

_ V T i = »+ г = _P _D„V

J p JbB JtT    ^p Р B ^y Р ^Р p T T       ^{v 7}

Здесь D_B - броуновский коэффициент диффузии, моделируемый уравнением Эйнштейна - Стокса:

D B

^k B ^T

^{3 n} H w d p

где k_B - постоянная Больцмана и d_p - диаметр частицы. Коэффициент термодиффузии D T является функцией температуры и вида молекул и рассчитывается как

D_T = 0,26

^ w ____ Н w

( 3 ^ w ■< p ) Р w

ф p .

где A_p - теплопроводность частиц.

Уравнения переноса импульса для молекулярных фаз запишем как

^( ф p Р p ^u p ^{) +} ’^- ( ф p ⁽Р p ^u p ® ^u p ) ) =

= -фpVpp + V ■ |фpTp ) + Md + Mg + SMp , где тензор напряжений имеет вид:

2        Л

^T p = H p |^{V u} p ^{+ ( V u} p ) -jO p ’ u p J .

Здесь M d и M _g - объемные плотности межфазных сил, S_Mp - перенос импульса между фазами, g _p -коэффициент второй вязкости. В уравнении (6) мы учли влияние двух соответственно силы Стокса и сила плавучести из-за разности плотностей фаз:

^M d = 187^ l u w - u p ) , ^M g = ( Р p -Р w ) g .      ( ⁸ )

d _p

Поскольку в реакции ПЦР объемная плотность молекулярных фаз всегда значительно меньше единицы, то в уравнении переноса импульса для растворителя можно положить ф ~ 1, и с учетом несжимаемости жидкости (2) в приближении Хеле -Шоу оно принимает вид:

f Эи„  6/

Р   —w + — (u -V) u =

Рw I                  w wI lo t 5

2      12ц

= ^-V p w ⁺ Н w ^{V u} w ^- —w 2 ^u w ⁺ Р w g .

^|5- l )

В уравнении (9) трение вязкой жидкости о широкие стенки кюветы приводит к появлению коэффициента 6/5 у нелинейного слагаемого в левой части, а также силы сопротивления в правой части уравнения [20].

Уравнения переноса тепла запишем как

д

( ф а Р а e а ) ^{+ V -} | ф а Р а ^U а e а ) =

= ’- | ф „ Х „ ’ Т а ) + ST- а .

где е_а - внутренняя энергия фазы а ; S_Ta - молекулярный перенос энергии между фазами.

В модели, описываемой уравнениями (2)-(10) предполагается несжимаемость жидкости, отсутствие внутреннего тепловыделения, отсутствие передачи импульса, связанного с межфазным массопереносом.

Уточним теперь источниковое слагаемое S p в правой части уравнения (2), которое включает в себя информацию о кинетике реакции ПЦР. Генерация и расход компонентов ДНК в результате температурнозависимых химических реакций первого порядка происходит циклически в три стадии:

• 1.    денатурация

• 2.    отжиг

• 3.    элонгация

dsDNA —— 2 ssDNA при температуре Td = 95°С;

ssDNA —-—> aDNA при температуре Ta = 55°С;

aDNA '  > eDNA при температуре Te = 72°С. Для скоростей реакций справедливы соотношения [11-13]:

rd = kd exp (-(T - Td)/2°d),

ra = ka exP (-(T - Ta ) / ^a ) ,         (11)

re = ke exP (-(T - Te ) 2^2 ) , где ki обозначают константы скоростей реакций, протекающих в идеальных условиях, а коэффициенты дисперсии  σi вычисляются для определенной конфигурации амплификатора и тепловых граничных условий. Эти величины являются постоянными. В формулах (11) будем использовать следующие значения: Td = 95°С, Ta = 55°С, Te = 72°С, оd = 5 K, о a = 5 K, о e = 2,5 K, kd = ka = 2 ke =1, s-1 [12; 13].

Химические уравнения можно записать в виде кинетических     соотношений,     описывающих массообмен между фазами. Таким образом, в правой части уравнений (2) добавляются следующие источники массы:

^S dsDNA = ^Р p ^{( 2} w aDNA k e - w dsDNA ^k d ) ’

^S ssDNA = ^Р p ⁽ w dsDNA k d - w ssDNA ^k a ) ’         ⁽¹²⁾

^S aDNA = ^P p ⁽ w :s:sDNA^ka - waDNA^ke ) •

Как известно, некоторые свойства жидкостей имеют зависимость от температуры. Для точности работы модели имеет смысл учесть в математической модели эти соотношения. В частности, для воды использовались будем использовать аппроксимации:

p[ kg / m ³ ] = 0,0000631 • T ³ - 0,06 • T ² +

+ 18,9 • T - 950,7;

^[ Pa x s ] = 3,85 • 10 - ¹⁶ • T ⁶ - 9,08 • 10 - ¹³ • T ⁵ +

+ 8,90 • IO ^{- 10} • T ⁴ - 4,65 • IO ^{- 7} • T ³ +                  (13)

+ 1,3640 - 4 • T ² - 0,0212 • T + 1,38;

k[ K /( m x K )] = 7,9840 ^{- 9} • T ³- 1,58•Ю ^{- 5} • T ² +

+ 0,00895 • T - 0,869.

Уравнения (2)-(13) содержат также некоторые свойства частиц, а именно диаметр d p и плотность р _p . И это самый тонкий момент, так как молекулы ДНК по своей природе имеют крайне гетерогенный и неизотропный характер. Как отмечено выше, фактически молекулы ДНК - длинные линейные молекулы. В некоторых работах при моделировании конвективной ПЦР молекулы ДНК считаются сферическими со специальным гидродинамическим диаметром d p , который можно приблизительно оценить на основе уравнения Эйнштейна - Стокса (4). Мы принимаем это допущение в данной работе, но отмечаем, что этот вопрос ждет своего дополнительного исследования.

Коэффициенты броуновской диффузии для молекул dsDNA и ssDNA были определены экспериментально в работе [21], но эти результаты справедливы лишь для коротких частей ДНК. Например, для обрывка молекулы dsDNA , имеющего 900 пар оснований, коэффициент диффузии был оценен как D B = 5,640^-12 м²/с. При этом гидродинамический диаметр оказался приблизительно равным d p = 0,088 мкм. Для молекул ssDNA , имеющих 900 оснований, те же величины были оценены как D B = 7,540^-12 м²/с и d p = 0,066 мкм. Результат выглядит логичным, так как двухцепочечная ДНК более массива и, очевидно, менее подвижна. При учёте этих результатов стоит помнить, что полная длина молекулы ДНК у человека примерно 3 миллиарда пар оснований. При этом обрывки ДНК, которые встречаются в приложениях могут быть весь разными по длине. Другим параметром частиц является плотность, которая для молекул ДНК принимает значения близкие к р _p = 1,7 г/см³ [22].

Граничные условия задавались следующим образом. На всех стенках ячейки скорость принималась равной нулю, то есть кювета полагалась замкнутой. Через боковые стенки отсутствует поток тепла q и дисперсных фаз J i . В начальный момент времени жидкость покоится, а в ячейке присутствует только молекулы dsDNA с объёмной долей ф _dsDN A = 10^-10, равномерно распределенные по объему. Такая объемная концентрация соответствует примерно 300 молекулам ДНК размером в 900 пар оснований на один микролитр. Согласно литературе [8] объем капилляра в микрочипе для конвективной ПЦР составляет порядка 1-50 мкл. Таким образом, речь идёт о тысячах молекул.

Итак, граничные и начальные условия имеют вид:

у = 0: u = 0, T = T H , - n • J i = 0;

у = y l : u = 0, T = T_c ,   - n • J = 0;

x = 0: u = 0, - n • q = 0, - n • J i = 0;

x = h : u = 0, - n • q = 0, - n • J i = 0;

t = 0:

u = 0,

T = T + ⁽ T C ^- T H ⁾ у , H      y h

Ф . = 10 - 10 , Ф ssDNA = 0, Ф aDNA = 0.

Таким образом, эволюционная задача (2)-(14) представляет собой замкнутую систему уравнений и граничных условий для скоростей и объёмных долей фаз, поля температур. Задача содержит следующие входные параметры, которые могут в определенной степени варьироваться: Y, 3 - аспектные соотношения, определяющие размеры ячейки. Все остальные величины определены.

Численная реализация

Проблема решалась с помощью программного пакета для моделирования жидкости ANSYS CFX (лицензия, выданная Пермскому национальному исследовательскому политехническому университету). Инструмент ANSYS CFX базируется на решении методом контрольных объемов уравнений Навье -Стокса, а в качестве входных геометрических данных используется сеточное разбиение области течения. Основные интегральные уравнения сохранения массы, количества движения и растворенных веществ решаются в размерной форме. Для решения эволюционных задач в частных производных ANSYS CFX использует единственный решатель Backward Euler (также известного как обратный метод Эйлера) -это неявный решатель, который использует формулы обратного дифференцирования с точностью первого или второго порядка. Метод Backward Euler известен своей стабильностью. Тем не менее, он в некоторых ситуациях может иметь серьезные демпфирующие эффекты, особенно метод первого порядка. Это может привести к численному решению более гладкому, чем решение системы дифференциальных уравнений. В настоящей работе для расчетов по эволюционной задаче был выбран решатель Backward Euler второго порядка точности, обеспечивающий оптимальное сочетание стабильности и скорости вычислений и меньшее влияние демпфирующих эффектов. Благодаря наличию универсального решателя пользователи ANSYS CFX не обременены выбором и не нуждаются в проведении серии дополнительных верификационных и валидационных расчетов с целью выявления наиболее оптимального для моделирования решателя. При этом, разумеется, следует выполнить верификацию вычислений с целью определить погрешности, связанные с дискретизацией расчетной области.

Вычисления показали большое влияние таймстеппинга на устойчивость и точность решения. ANSYS CFX предлагает варианты с адаптивным и ручным выбором шага по времени. Мы использовали адаптивный метод, при котором решатель ANSYS CFX самостоятельно выбирает временной шаг, исходя из критерия минимизации ошибки вычислений.

Расчетная область разбивалась триангулярной сеткой со сгущением вблизи границ. Было выполнено

исследование независимости решения от сетки с последовательно уточненным разрешением сетки в диапазоне от 10⁴ до 10 5 элементов. Контролировались усредненные по объему модуль скорости, температура и объемная доля дисперсных фракций после проведения реакции ПЦР в течение 200 с. Для основных расчетов использовался минимальный размер сетки, при котором уменьшение шага в 2 раза приводило к изменению характеристик течения не более чем на 10 %.

Валидация модели

В данном разделе приводятся результаты сравнения разработанной математической модели с известными результатами в литературе. Удобной для сравнения задачей, которая схожа по постановке с рассматриваемой в данной работе конвективной ПЦР, является тепловая конвекция наножидкости в замкнутой петле [2]. Было проведено два теста, которые обсуждаются ниже.

Бенчмарк № 1

Валидация на достоверность описания термофореза проведена на основе теста, предложенного в работе [2] для наножидкостей. Суть его в следующем. Рассматривается стационарная наножидкость с постоянными теплофизическими свойствами в домене x е [0, L ] с линейным распределением температуры:

T = T ₀ + xG,               (15)

где G - постоянный положительный градиент температуры, T ₀ - температура при x = 0. Таким образом, температура растет с ростом координаты x . Объёмная доля наночастиц ф определяется

уравнением:

d φ dt

„ („„  „ v t у

V- D „Vф + D_T --- .

BT

Предполагая, что свойства растворителя постоянны, для коэффициентов броуновской диффузии и термофореза можем записать:

D_B = aT, D_T = Ьф, a =

k_B 3πμ _wd_p

, b =

0, 26λ w

2^ w + ^ p

V w .(17)

Таким образом, тест представляет собой

одномерную на отрезке x е [0, L ] задачу:

d φ dt

X f     , x\^d ф

— a ( T + xG )-- +

Xx ^ ^u ’dx

bG   У

φ,

T ₀ + xG J

с заданными на границах отрезка граничными условиями, а также начальным условием для объёмной доли наночастиц:

dφ bG x = 0: aT--1--ф = 0, 0 dx T       ,

x = L: a (To + LG)dф + bG ф = 0, v 0     ’Xx  To + LG t = 0: ф = ф0.

Рис. 2 представляет результаты сравнения решения задачи (19), полученные в работе [2], и результаты, полученные на основе модели, развитой в настоящей работе для следующих значений параметров: v = 0^-6 м²/с,      Л _w = 0,6 Вт/(м^К),      Л p = 25 Вт/(м^К),

L = 2,5 мм, ф₀ = 0,03. Градиент температуры G = 1,640 4 К/м соответствует перепаду температуры 40 К на отрезке 2,5 мм. Сравнение показывает, что результаты хорошо согласуются и, следовательно, предлагаемая в настоящей работе модель правильно описывает термофорез субмикронных частиц.

Результаты также наглядно показывают, что благодаря термодиффузии концентрация наночастиц в направлении обратном к градиенту температуры значительно увеличивается, так как частицы дисперсной фазы получают дополнительный импульс со стороны более горячих молекул растворителя.

Бенчмарк № 2

Для проверки того, насколько достоверно ЭЭ-модель (2)-(14) описывает ПЦР, было проведено сравнение с данными, получаемыми в рамках однофазной модели многокомпонентного (МК) истинного раствора молекул, которая подробно описана в ряде работ [11-13] и широко используется в настоящее время при моделировании конвективной ПЦР. Напомним, что в истинных растворах нет четких границ между фазами, компоненты перемешаны на молекулярном уровне и их нельзя разделить. Математически движение раствора описывается одним скоростным уравнением Навье - Стокса, а для компонент записываются транспортные уравнения со слагаемыми, отвечающими за конвективный снос.

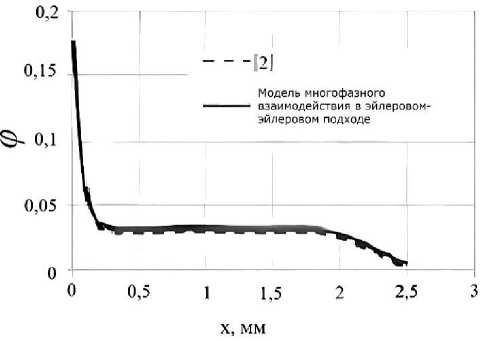
Рис. 2. Профили концентрации наночастиц в 1- D домене при t = 1000 с. Представлены решения, полученные в работе [2] для наножидкости (штрихованная линия), и результаты, полученные в рамках нашей модели для конвективной ПЦР (сплошная линия)

Содержание молекул в этом случае характеризуют молярные концентрации компонент.

Полная система уравнений конвекции-реакции-диффузии для гомогенной неизотермической смеси имеет следующий вид:

р| — + — (о -V) u =-V p + p V ²u--u + p g ,

Id t   5 ⁽      ) J                       ( 5 - 1 ) ²

div u = 0,

P С p (1 T + ( u -V ) T У k V ² T ,

Ц + (u-V)Ci = DiV2Ci + ri , где ci - молярные концентрации dsDNA, ssDNA и aDNA, Di - соответствующие коэффициенты диффузии компонент. Скорости реакции ri определим следующим образом:

rdlsDNA = kefeCaDNA  kXfXCXsDNA , rssDNA   2kXfXcdsDNA  kafaCssDNA, raDNA = kafaCssDNA — kefeCaDNA ,

f          (t - Ti)

fi = exp ^{- V} ~ 2

I       ² ° i

.

Константы скоростей реакций k i ( i = d , a , e ) и дисперсии g i имеют такой же смысл, что в выражениях (11) для ЭЭ-метода.

Уравнения (20), (21) следует дополнить граничными и начальными условиями, которые формулируются аналогично (14):

у = 0: u = 0, T = T_H , - n - J_; = 0;

у = у l : u = 0, T = T_c , - n - J_; = 0;

x = 0: u = 0, - n - q = 0, - n - J, = 0;

x = h :   u = 0,   - n - q = 0, - n - J, = 0;

t = 0: u = 0, T = T h + ( T c - T h ) у / у h , ^C XsDNA = ^C 0 , c ssDNA = ⁰, ^C aDNA = ⁰-

Краевая задача (20)-(22) может использоваться как бенчмарк для проверки предлагаемой в работе ЭЭ модели ПЦР. Результаты, полученные в рамках традиционного подхода, будут обсуждаться ниже в контексте новых результатов данной работы.

Численные результаты

Основным результатом в задачах по исследованию протекания ПЦР стандартно считается определение времени удвоения числа молекул ДНК, находящихся в амплификаторе. Кроме того, к результатам численного моделирования, которые можно использовать для сравнения различных моделей, можно отнести поля скорости, температуры, скоростей реакции, распределения молекул.

Значения управляющих параметров в расчетах были зафиксированы. Для более точной реализации

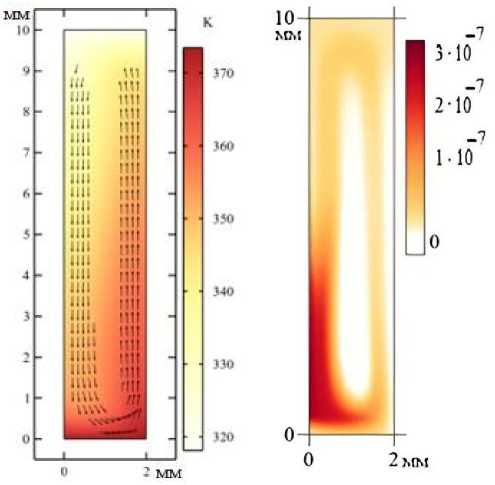
Рис. 4. Поле объёмной доли молекул dsDNA при t = 400 c

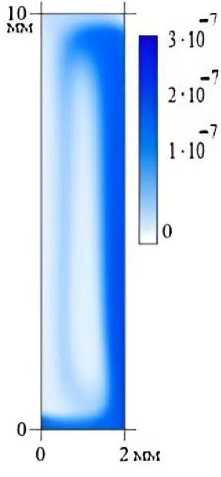
Рис. 5. Поле объёмной доли молекул ssDNA при t = 400 c

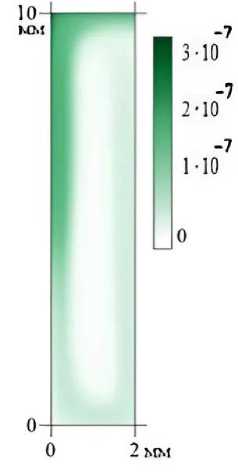
Рис. 6. Поле объёмной доли молекул aDNA при t = 400 с

Рис. 3. Установившиеся поля скорости и температуры ( t = 400 c)

приближения Хеле – Шоу требуется выполнение условия δ ≪ 1. Однако, у этого есть своя цена: при слишком малых толщинах ячейки из-за силы сопротивления стенок скорость течения значительно снижается и это отрицательно сказывается на общем времени амплификации ДНК. Поскольку основной идеей конвективной ПЦР является именно ускорение реакции, оптимальным было бы подобрать значение δ таким образом, чтобы приближение Хеле – Шоу ещё бы выполнялось, но скорость течения была бы максимальной. Таким образом, мы в расчетах зафиксировали следующее значение этого параметра: δ = 0,2, которое находится на самом краю корректности применения приближения Хеле – Шоу. Значения другого геометрического параметра определим как γ = 5, обеспечивая достаточно протяжённую вертикальную дистанцию для молекул ДНК. Стоит напомнить, что реакция происходит не мгновенно, а занимает некоторое время. Поэтому каждая молекула ДНК должна находится в реакционной зоне с комфортной температурой определенное время.

Анализ уравнений (2)–(5) показывает, что термофорез создает дополнительную адвекцию, влияющую на дисперсные фазы таким образом, что они постепенно перемещаются из горячих областей в более холодные. Это влияет на ход реакции ПЦР, но степень изменений зависит также от концентрации дисперсной фазы: чем больше ее объёмная доля в растворе, тем сильнее эффект термодиффузии и влияние на ПЦР.

Наши численные расчеты подтверждают эти соображения выше. Было показано, что пока средняя объёмная доля каждой дисперсной фазы не превышает значения 10–5, результаты ЭЭ модели и однофазной МК моделей остаются качественно близкими. При выбранном наборе параметров, начальных и граничных условий количество дисперсной фазы увеличивается со временем по закону близкому к экспоненциальному и достигает объемной концентрации 10–5 примерно за 600 с. Финальное течение имеет стационарный характер, а время установления полей скорости и температуры составляет порядка 1 мин. На рис. 3 показана структура установившихся полей скорости (векторное поле) и температуры (расцветка) в момент времени t = 400 с, полученная в ЭЭ модели конвективной ПЦР. Как видно из рисунка, течение представляет собой одновихревое подъёмно-опускное течение. Конечно, выполняется это лишь с некоторым оговорками, потому что в углах ячейки живут неизбежные мелкомасштабные вихорьки. Как показывает моделирование, в установившемся течении при максимальной по ячейке скорости 1,3 мм/с, жидкость вместе с частицами совершает полный оборот примерно за 20 с. Наиболее быстрые течения наблюдаются на расстоянии 0,2–0,3 мм от каждой из боковых стенок.

На рис. 4–6 приведены также поля объёмной доли молекул ДНК через 400 с после начала эволюции. Можно заметить, что двухцепочечная ДНК концентрируется в нижнем левом углу ячейки (рис. 4), в то время как одноцепочечные молекулы предпочитают правую часть кюветы (рис. 5). Молекулы с отжигом собираются в верхней левой части (рис. 6), отражая фазы протекания реакции ПЦР. Отметим, что однофазная модель (20)–(22) дает молекулярные поля с очень похожей структурой.

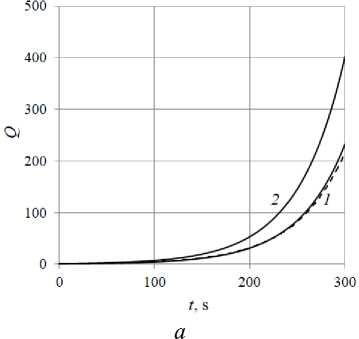
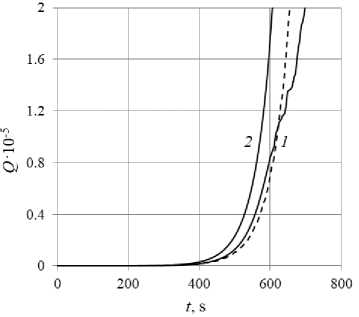
В задачах ПЦР большое значение имеет темп роста числа молекул: одного вида или общего их количества. На рис. 7, а приводится зависимость общего числа молекул трех видов (dsDNA, ssDNA, aDNA) в зависимости от времени за первые 300 с реакции, а на рис. 7, б – за 700 с. В ЭЭ многофазной и однофазной МК моделях мера числа молекул различна. Поэтому для сравнения использовалось количество молекул по отношению к таковому в начальный момент времени Q. Однофазная модель показывает зависимость Q(t) наиболее близкую к экспоненте. Для ЭЭ модели в целом график проходит ниже, т.е. интенсивность реакции оказывается меньшей, а время удвоения числа молекул больше. При t < 300 с график близок к экспоненте, но при больших временах получается неровным и все более отклоняющимся от экспоненты. Наблюдения за структурой полей скорости и молекул показывает, что при t > 600 с течение становится нестационарным, в то время как в однофазной модели течение стационарно и сохраняет структуру, показанную на рис. 3–6, неограниченно долго по времени. Для проверки того, что является причиной таких различий в ходе реакции в двух сравниваемых моделях, был проведен расчет с помощью ЭЭ модели с отключенным термофорезом. В итоге вплоть до времен порядка 1000 с результаты с точностью 1–3 % совпадают с результатами однофазной модели. Это говорит о том, что термодиффузия в задачах c конвективной PCR может существенно влиять на результаты численного моделирования.

Механизм влияния термофореза на протекание конвективной ПЦР можно объяснить, наблюдая за скоростью конвективного течения и полями молекул ДНК. Отметим, что для многофазного течения под скоростью и температурой понимаются скорость и температура растворителя, т.к. его объемная доля в ходе конвективной ПЦР намного превышает долю молекул ДНК. На рис. 8 представлен график эволюции средней по расчетной области абсолютной скорости для однофазной и многофазной ЭЭ модели после периода установления стационарной конвекции. В однофазной модели поля температуры и скорости после установления не меняются, а поля молекул ДНК сохраняют конфигурацию в пространстве, хотя при этом растет объемная концентрация дисперсных фаз. В модели ЭЭ с учетом термофореза некоторое время

(порядка 400 с) сохраняется аналогичная картина. В интервале времени от 400 до 600 с течение начинает замедляться. Торможение конвективной циркуляции вызвано конкуренцией со стороны адвекции, обусловленной термофорезом. Особенно сильно это проявляется на поле молекул dsDNA , которое, как видно из рис. 4 формирует облако вблизи горячей стенки в области нисходящего потока. Конвективный поток в области скопления молекул dsDNA направлен вниз, а адвективный поток – вверх, от горячего к холодному, т.е. они направлены в разные стороны. Такое противодействие приводит к снижению скорости молекулярной фракции dsDNA и смещению облака молекул в область более низких температур. Анализ выражений (2)–(5) показывает, что адвекция, вызванная термофорезом, пропорциональна концентрации молекул. В самом начале реакции ПЦР объёмная доля молекул крайне мала (φ dsDNA = 10^–10), но в ходе реакции она растет по экспоненциальному закону. Поэтому в первые 400 с влияние термофореза проявляется относительно слабо и заметно только в замедлении реакции (рис. 7, а ). Однако позже объемная доля молекул становится настолько высокой (φ dsDNA ≈ 10^–5), что вследствие межфазной передачи импульса замедляется движение всего раствора. В интервале времен t = 400–600 с, как видно из рис. 8, средняя скорость конвективной циркуляции уменьшается вдвое. При t = 600 с влияние термофореза становится настолько большим, что облако молекул dsDNA всплывает вверх в область более холодной жидкости, при этом дисперсная фаза увлекает своим движением весь раствор. Этого оказывается достаточно, чтобы изменить циркуляцию на противоположную. В дальнейшем конкуренция конвективной циркуляции и адвекции, вызванной термофорезом, приводят к возникновению нерегулярных колебаний течения со сменой направления циркуляции течения. Колебания при термодиффузии известны и описаны литературе (см., например, недавнюю работу [23] и ссылки внутри). По-видимому, развивающаяся постепенно

б

Рис. 7. Зависимость количества молекул в ячейке от времени при малом ( а ) и большом ( б ) относительном содержании дисперсной фазы: для ЭЭ модели ( 1 ), для однофазной модели ( 2 ) и экспоненциальная аппроксимация для ЭЭ модели (штриховая линия)

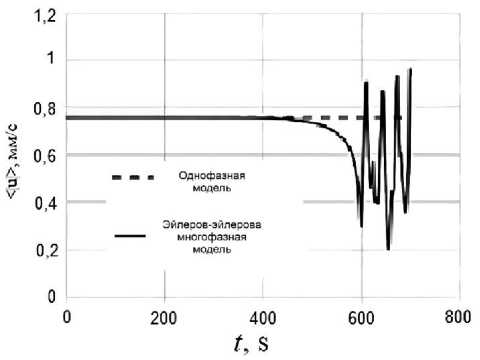
Рис. 8. Эволюция среднего по расчетной области модуля скорости нестационарность течения является неблагоприятным фактором конвективной ПЦР, но процесс в микрореакторах развивается медленно, позволяя накопить достаточно материала за несколько минут протекания стационарной реакции.

Заключение

Разработана модель полимеразной цепной реакции, в которой молекулы ДНК рассматриваются как дисперсная среда и к ней применяется Эйлер – Эйлеров метод для многофазных сред. Проверочные тесты показали, что результаты, даваемые моделью, вполне достоверные.

К преимуществам обсуждаемого метода можно отнести возможность учета влияния на движение