Эконометрическое моделирование производства продукции крестьянских (фермерских) хозяйств

Введение. В настоящее время в РФ наблюдается процесс формирования новых подходов в отрасли сельского хозяйства. Их ориентация определена изменениями, связанными с открытиями новых методик моделирования, основанных прежде всего на обработке огромных массивов информации, а также технологических инновациях [3]. Как и прежде, производство крестьянско-фермерских хозяйств определено рядом факторов, которые оказывают на него значительное влияние, часть из которых не зависит от самого производителя или экономической среды региона или страны [2; 11].

Отрасль сельского хозяйства очень чувствительна к изменениям, происходящим как на внутреннем рынке, так и глобально. Стоит обратить внимание, что деятельность отдельно взятого крестьянско-фермерского хозяйства предопределена прежде всего природно-климатическим аспектом. Колебание погодных условий может повлечь за собой плохую урожайность сельскохозяйственных культур [6]. Вследствие этого страдает животноводство, происходит уменьшение поголовья скота из-за нехватки кормов. Параллельно с этим в результате нехватки сырья страдают и другие отрасли.

Также стоит учесть тот факт, что экономические просчеты, возникшие в результате неправильного прогнозирования деятельности в отрасли, могут оказать негативное воздействие на урожайность. Примером этому служит то, что часть стран выбрала приоритетным направлением в растениеводстве посадку технических культур с целью дальнейшей их переработки и получения органического топлива [7]. Из-за глобального ухудшения климата произошло то, что в результате снизился объем продовольствия, а глобальные темпы прироста населения третьего мира привели к падению равновесия между спросом и предложением. В конечном счете увеличились цены на товары сельскохозяйственной отрасли.

Таким образом, процессы, которые происходят в экономике, ставят перед организациями сельскохозяйственной отрасли задачу наращивания объемов производства. В связи с этим актуальность расширения крестьянских (фермерских) хозяйств заключается в дополнительном поддержании данного вектора. Целью построения прогнозных моделей, отражающих дальнейшую динамику роста производства продукции, является оценка дальнейших перспектив и сценариев развития агропромышленного комплекса в целом и крестьянских (фермерских) хозяйств в частности.

Материалы и методы

Рассматривая в динамике процесс наращивания производства всех отраслей сельского хозяйства, крестьянские (фермерские) хозяйства выделяются стабильным и планомерным ростом [8]. В связи с этим модели, которые были отобраны для прогнозирования, базируются на ретроспективных данных ряда, поскольку прогнозирование с использованием множества объясняющих (экзогенных) переменных невозможна в связи с их мультиколлинеарностью.

В общей сложности продукция крестьянских (фермерских) хозяйств подразделяется на продукцию от растениеводства и продукцию животноводства. Фактором, косвенно отражающим климатические и другие условия, влияющие на объемы продукции растениеводства, является урожайность. Продукция крестьянских (фермерских) хозяйств от животноводства прямо зависит от расхода кормов, которые являются одним из главных затратных ресурсов [9]. Таким образом, выборка включает в себя 5 показателей. Рассматриваемый период: 2010– 2020 годы. В таблице 1 представлены исходные данные для эконометрического анализа.

Таблица 1

Исходные данные 1

Показатель/год	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020
1. Продукция крестьянских (фермерских) хозяйств - растениеводство, млрд р. [Pr]	133,5	229,1	221,3	277,8	330,4	442	513	499,2	530,2	636,6	792,7
2. Урожайность сельскохозяй ственных культур, ц/га [U]	18,3	22,4	18,3	22	24,1	23,7	26,2	29,2	25,4	26,7	28,6
3. Продукция крестьянских (фермерских) хозяйств - животноводства, млрд р. [Pj]	53,9	65,1	76,2	83,5	99,3	109,1	121,7	136,4	139,8	156,7	171,5
4. Расход кормов в животноводстве, млн т [R]	96,9	98,2	101	100,8	104,8	104,5	106,7	107	105,6	105,9	106,2
5. Продукция крестьянских (фермерских) хозяйств, млрд р. п.1 + п.3 [P]	187,4	294,2	297,5	361,3	429,7	551,1	634,7	635,6	670	793,3	964,2

На рис. 1 представлены графики динамики представленных ранее показателей.

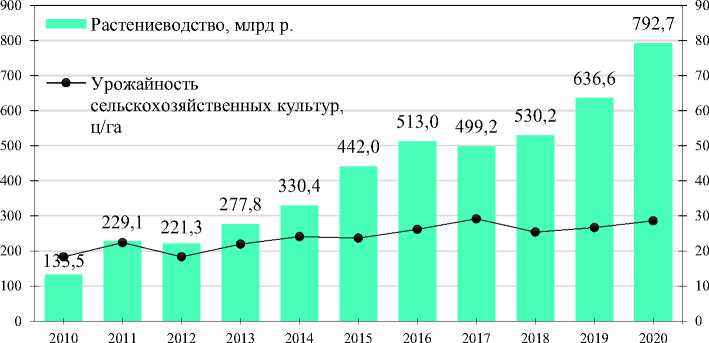
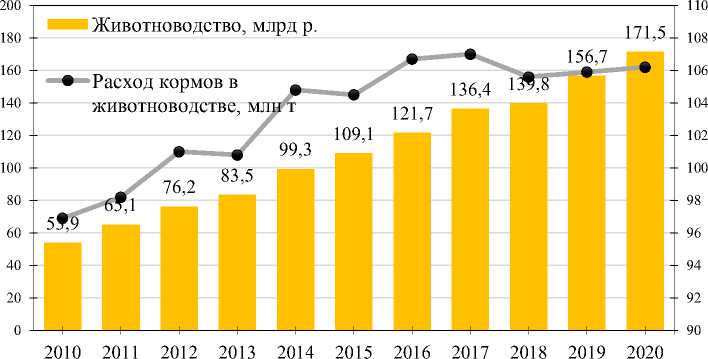
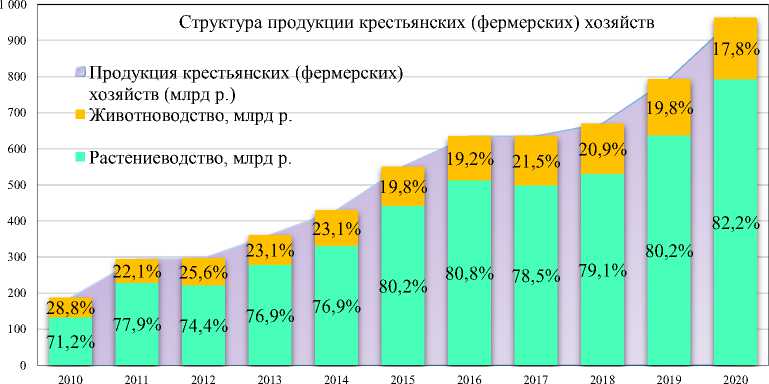
Рис. 1. Динамика и структура продукции крестьянских (фермерских) хозяйств

Отметим, что несмотря на то, что урожайность держится приблизительно на одном уровне, крестьянские (фермерские) хозяйства смогли нарастить объем продукции от растениеводства, что свидетельствует об экстенсивном расширении и эффективном использовании посевных площадей. Также на рис. 1 видно, что наибольшую долю продукции составляют товары растениеводства. Говоря о животноводстве, отметим, что рост продукции прямо зависит от расхода кормов.

Подтвердим это статистически, высчитав коэффициенты корреляции: corr(Pr; U) = 0,876580972 — корреляция между продукцией растениеводства крестьянских (фермерских) хозяйств и урожайностью; corr(Pj; R) = 0,887218928 - корреляция между продукцией животноводства и расходованием кормов животноводства. Как мы видим, существует высокая прямая корреляционная связь. Оценим влияние урожайности на продукцию растениеводства и расходование кормов на продукцию животноводства путем построения соответствующих эконометрических линейных моделей (таблица 2).

Таблица 2

Линейные модели взаимосвязи данных

Модель: Pr = 47,8949 × U - 734,688
Переменная	Коэффициент	Ст. ошибка		t-статистика	p-значение
const	-734,688	213,280		-3,445	0,0073 ***
U	47,8949	8,76498		5,464	0,0004 ***
Среднее зав. перемен        418,7091			Ст. откл. зав. перемен		199,9020
Сумма кв. остатков         92551,52			Ст. ошибка модели		101,4076
R-квадрат	0,768394		Испр. R-квадрат		0,742660
F(1, 9)	29,85913		Р-значение (F)		0,000398
Лог. правдоподобие        -65,31526			Крит. Акаике		134,6305
Крит. Шварца	135,4263		Крит. Хеннана-Куинна		134,1289
Параметр rho	0,013165		Стат. Дарбина-Вотсона		1,711650
Модель: Pj = 9 ,55163 × R – 877,522
Переменная	Коэффициент	Ст. ошибка		t – статистика	p – значение
const	-877,522	171,312		-5,122	0,0006 ***
R	9,55163	1,65560		5,769	0,0003 ***
Среднее зав. перемен        110,2909			Ст. откл. зав. перемен		38,48027
Сумма кв. остатков         3151,626			Ст. ошибка модели		18,71311
R-квадрат	0,787157		Испр. R-квадрат		0,763508
F(1, 9)	33,28477		Р-значение (F)		0,000270
Лог. правдоподобие        -46,72611			Крит. Акаике		97,45221
Крит. Шварца	98,24800		Крит. Хеннана-Куинна		96,95058
Параметр rho	0,830999		Стат. Дарбина-Вотсона		0,579093

Полученные модели, отображенные в таблице 2, считаются статистически значимыми согласно критерию F-Фишера, статистически значимы и коэффициенты, причем на уровне 1%. R-квадрат выше 75%, что свидетельствует о средней точности моделей. В среднем из-за увеличения урожайности на 1 ц/га продукция от растениеводства возрастает на 47,89 млрд р. При увеличении же расхода кормов на 1 млн т продукция от животноводства возрастает в среднем на 9,55 млн р.

В статье [13] было продемонстрировано, что увеличение урожайности сельскохозяйственных культур значительно снижает уровень бедности. Урожайность, масса собранной растениеводческой продукции на определенной территории, зависит от следующих групп факторов: технологические (методы ведения сельского хозяйства, управленческие решения и т. д.), биологические (болезни, насекомые, вредители, сорняки) и экологические (климатические условия, плодородие почвы, рельеф местности, качество воды и т. д.). Эти факторы объясняют различия в урожайности в разных регионах мира. Результаты приведенного исследования указывают на обоснованность применения в качестве предикторов разработанных моделей урожайности и затрат на корма. Результаты моделирования указывают на целесообразность внедрения более эффективных технологий в отрасли растениеводства и животноводства. Кроме этого, данный факт позволяет взвесить все риски при проведении планирования производства, а также осуществить наиболее успешный выбор места дислокации крестьянского (фермерского) хозяйства.

Далее построим прогнозные модели производства и выведем их основные характеристики на рис. 2.

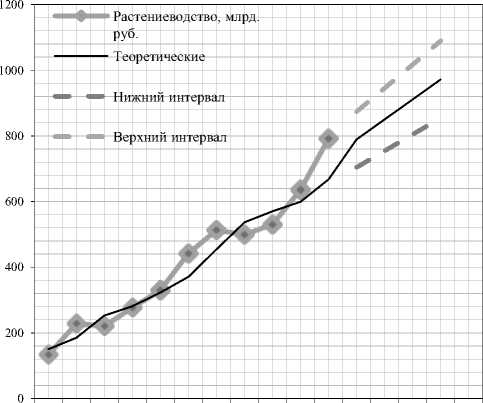
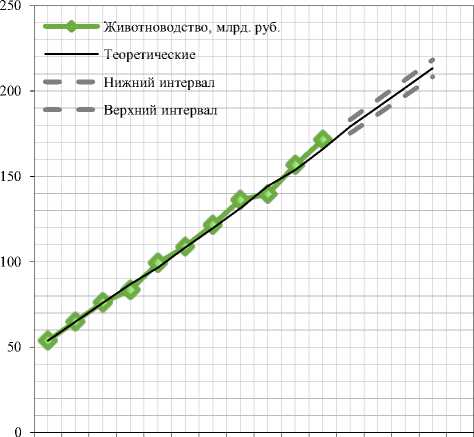
Построенные линейные модели регрессии характеризуются высокими коэффициентами детерминации и могут использоваться при прогнозировании. Однако линейная модель для прогнозирования производства продукции от растениеводства имеет один из коэффициентов, значимость которого определена на уровне всего лишь 10%. Критерии нормальности распределения остатков не выполняются. Во всем остальном данные модели отлично демонстрируют свою эффективность. Определенный моделями тренд свидетельствует о дальнейшем росте объемов производства. При этом построенный доверительный интервал имеет достаточно узкий диапазон, что свидетельствует о высокой предсказуемости тренда. Поскольку в современных условиях рост производства происходит не только экстенсивным, но и интенсивным путем, то даже смелые экспоненциальные тренды имеют место быть.

Таким образом, преимуществом линейных моделей для данного конкретного случая можно считать их наибольшую точность прогноза, поскольку исходные данные имеют четкую линейную тенденцию. Однако для большинства случаев намного более точный прогноз имеют модели с «обучением» или экспоненциальным сглаживанием [1; 10]. К таким можно отнести модель Брауна и модель Хольта-Винтерса. При этом принцип их построения заключается в первичной оценке параметров a 0 и a 1 по первым 5 точкам данных, а далее коэффициенты корректируются по формуле:

a 0( t ) = a 0( t - 1) + ^a 1( t - 1) + ⁽¹ - P 2 ) • e ( t ). a 1(t ) = ^a1(t - 1) + ⁽¹ - ^{e )}2 ■ e ( t ) ;, где β — коэффициент дисконтирования данных, отражающий степень доверия к более поздним наблюдениям; α — параметр сглаживания (α =1-β); e — отклонение (остаточная компонента). При этом, рассчитывая в excel все основные параметры модели, параметр альфа корректируется под то значение, при котором существует наименьшая ошибка модели (S y ).

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА

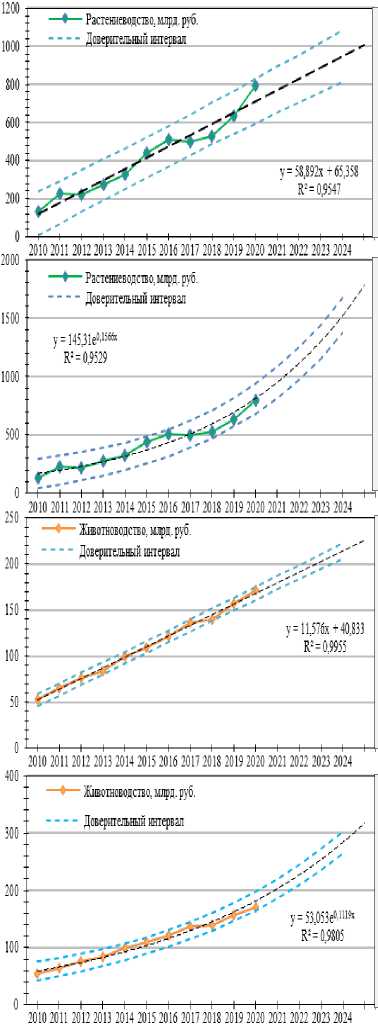
Рис. 2. Построенные модели регрессии

Переменная Коэффициент Ст. ошибка    t-статистика     p-значение const         65,3582       29,0009          2,254          0,0507 * t            58,8918       4,27594          13,77        2,36e-07 *** Линейная модель Среднее зав. перемен      418,7091    Ст. откл. зав. перемен      199,9020 Сумма кв. остатков       18100,86    Ст. ошибка модели       44,84648 R-квадрат                0,954703    Испр. R-квадрат          0,949670 F(1, 9)                     189,6906    Р-значение (F)             2,36e-07 Лог. правдоподобие      -56,34033   Крит. Акаике             116,6807 Крит. Шварца            117,4765    Крит. Хеннана-Куинна    116,1790 Параметр rho             0,138294    Стат. Дарбина-Вотсона    1,465890

Переменная Коэффициент Ст. ошибка t-статистика     p-значение const        145,3104351    0,086787224   1674,329794   4,92375e-26 *** t         0,156618511    0,012796078    91,3990482    1,13889e-14 *** Экспоненциальная модель Среднее зав. перемен     418,7091   Ст. откл. зав. перемен       199,9020 Сумма кв. остатков     0,162102219 Ст. ошибка модели       0,134206399 R-квадрат               0,9529    Испр. R-квадрат           0,9370305 F(1, 9)                     149,81    Р-значение (F)             6,50547e-07 Лог. правдоподобие      7,5875    Крит. Акаике               -11,175 Крит. Шварца           -10,3792   Крит. Хеннана-Куинна     -11,6744 Параметр rho           0,461695   Стат. Дарбина-Вотсона      1,0141

Переменная Коэффициент Ст. ошибка    t-статистика    p-значение const          40,8327        1,75076         23,32      2,33e-09 *** t            11,5764       0,258136         44,85       6,81e-012 *** Линейная модель Среднее зав. перемен     110,2909  Ст. откл. зав. перемен         38,48027 Сумма кв. остатков      65,96764  Ст. ошибка модели          2,707349 R-квадрат              0,995545  Испр. R-квадрат             0,995050 F(1, 9)                   2011,169  Р-значение (F)                6,81e-12 Лог. правдоподобие     -25,46030 Крит. Акаике               54,92061 Крит. Шварца           55,71640  Крит. Хеннана-Куинна       54,41897 Параметр rho           -0,340634 Стат. Дарбина-Вотсона      2,365421

Переменная Коэффициент Ст. ошибка     t-статистика       p-значение const        53,05268     0,036073        1470,6927      1,58185e-25 *** t          0,11187       0,00532         210,2716       6,33117e-18 *** Экспоненциальная модель Среднее зав. перемен     110,2909    Ст. откл. зав. перемен        38,48027 Сумма кв. остатков       0,0280    Ст. ошибка модели          0,055783 R-квадрат                0,9805    Испр. R-квадрат            0,977848 F(1, 9)                    442,4463    Р-значение (F)              5,81723e-09 Лог. правдоподобие      17,24449   Крит. Акаике               -30,48898 Крит. Шварца           -29,69318   Крит. Хеннана-Куинна       -30,9906 Параметр rho            0,672172   Стат. Дарбина-Вотсона       0,67239

Таким образом, для рядов исходных данных продукции крестьянских (фермерских) хозяйств модель Брауна имеет следующий вид (рис. 3).

S y	199,9019632
Eотн	10,30%
S	56,20310581
RS	2,925687207
е макс	124,3485512
е мин	-40,0841564
dw	1,18099056
t	2,262157163
Se	55,2680924
r	0,314368856
MAD	19,29868741
R²	0,920952796

S y	38,48026649
Eотн	2,05%
S	3,301484538
RS	3,044505792
е макс	5,547032731
е мин	-4,50435607
dw	2,018189371
t	2,262157163
Se	3,264237178
r	-0,20946207
MAD	1,09132123
R²	0,992638905

Рис. 3. Построение модели Брауна в Excel

Расчетное значение RS-критерия попадает в интервал критических значений, следовательно, выполняется свойство нормального распределения. Среднее абсолютное отклонение (MAD) находится на уровне 19,3 и 1,09 соответственно. Высчитанные коэффициенты детерминации, равные 92,1 и 99,26%, отражают высокую точность модели.

При этом ошиб ка прогноза находилась по формуле:

а*(1+4*(1-а)+5*(1-а)2+2*а(4-3*а)*1+2*а2

и =t*5e* J--------------(2   -------------- — для первого прогноза.

а*(1+4*(1-а)+5*(1-а) 2 +2*а(4-3*а)*2+2*4*а²

и = t * De * J-----------------(2   ----------------- — для второго, и т. д.

Полученные результаты моделирования по модели Брауна оказались отличными: несмотря на то, что ряд данных животноводства (млрд р.) имеет явно линейный тренд, модель показала прогноз, практически схожий с обычной линейной регрессией, а в случае с прогнозом по растениеводству данная модель гораздо более точнее и вероятнее показала тренд, который ориентировался на ретроспективные данные. В связи с этим, согласно построенной модели, рост продукции растениеводства в перспективе сначала замедлится, но потом вновь будет происходить наращение.

Далее выполним построение мультипликативной модели экспоненциального сглаживания Хольта-Винтерса. Сглаживание Хольта-Винтерса также называют тройным экспоненциальным сглаживанием, потому что у него три сглаживающих параметра (альфа, гамма и сезонный фактор — дельта) [4]. Чтобы выполнить моделирование по методу Хольта-Винтерса, необходимо сгладить исторические данные методом скользящего среднего, очистить данные от сезонной компоненты (в данном примере сезонность в данных не наблюдается). Вычисление и подбор параметров определяются в Excel опцией поиск решения (рис. 4).

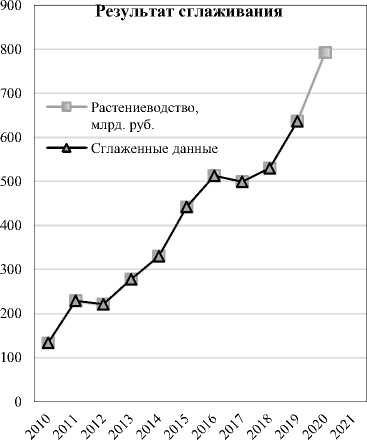
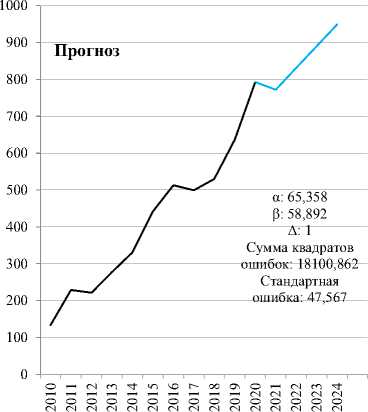
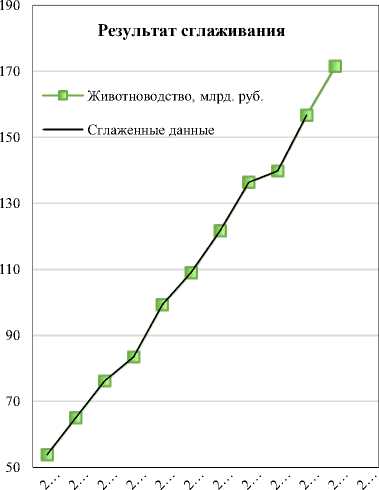
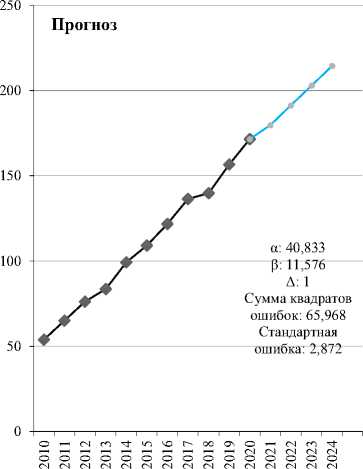
Рис. 4. Построение модели Хольта-Винтерса

Модель Хольта-Винтерса показывает аналогичные результаты модели Брауна. Но поскольку в нашем случае данные годичные и не содержат сезонной компоненты, главное преимущество данной модели незаметно. Построенные для двух рядов модели Хольта-Винтерса имеют маленькую стандартную ошибку модели, что свидетельствует об их высокой точности. Преимуществом данного метода является его универсальность и точность, как и модель Брауна [12].

Далее для анализа выберем построение нейронной сети. Поскольку ряд имеет линейный характер и не содержит сильных колебаний, построим модель одного и трех нейронов. Опишем формулой общую модель одного нейрона:

• ^Y = /^TANH^ ^-l к_ПХ_П; ^k1 — 3^E ^ -    , -   ^] ; ^k 4 ^E [[% _m j _n j, [ ^6X _ma -^{l ].}

Однослойная же модель нейронной сети имеет вид:

Y = k ₇ tanh(k ₆ tanh £ £-3 к_лх_л + k ₅ tanh £ £=1 k_nx_n );

• ^k1-4^{E [}-    , -    ]< ^k5,6 ^ ^[— ^ДЬ ^k7 ^ ^[ L ^xmin^J , 1^6х та- 1]

При этом гиперболический тангенс в Excel высчитывается функцией TANH(). Общая методика построения модели нейронной сети следующая: коэффициенты нейронной сети определяются поиском решения (Solver) с заданными условиями: k_1-3E [——, --³— ]; k₄E [[x _m i _n J, [6x _ma- l]. При этом лимитирующим (минимум, который определяет конечная функция) является сумма отклонений прогноза сети от фактических данных. Таким образом, по имеющимся данным определяются и корректируются коэффициенты, происходит нормирование и прогноз. Модель трех нейронов принципиально отличается от модели одного нейрона качеством обучения сети [5].

При этом необходимо учитывать наличие автокорреляции ряда. В нашем случае автокорреляция первого порядка для данных продукции крестьянских (фермерских) хозяйств — растениеводство — составляет 0,9596, а для животноводства: 0,993. Выполним построение нейронных сетей (рис. 5).

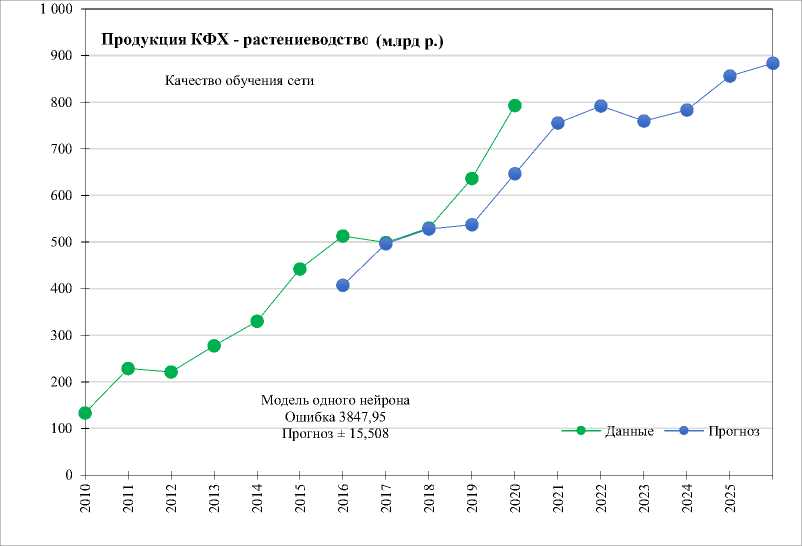
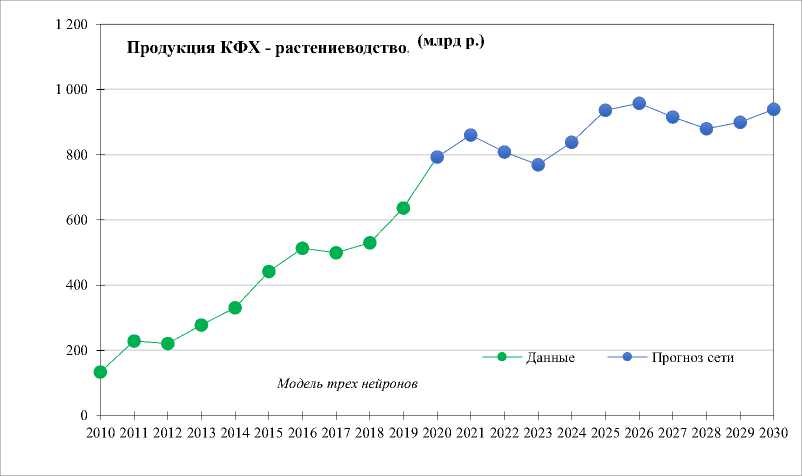
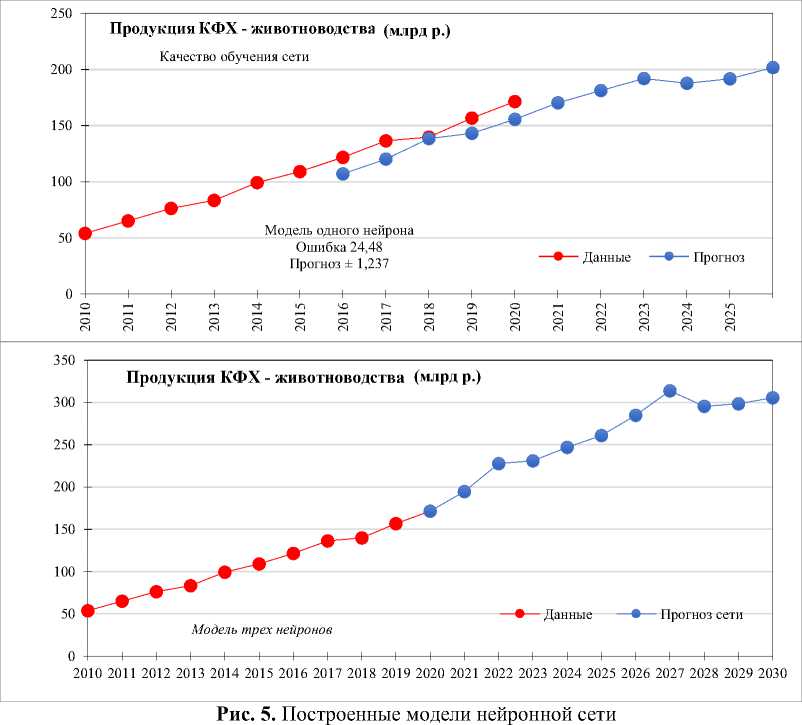
Таким образом, построенный прогноз по нейронной сети отражает динамику на предстоящие 7 лет и демонстрирует достаточно достоверный результат. Высокое качество обучения сети существенно сократило ошибку прогноза. Данный тип модели носит качественно другой характер, нежели рассмотренные ранее. Анализируя ретроспективные данные, нейронная сеть на основе формирования входных коэффициентов генерирует значения, наиболее близкие по динамике и колебанию данных.

Результаты

Эконометрическое моделирование позволяет оценить, какие производственные показатели будут ожидать фермерские хозяйства России в перспективе. Построенная экспоненциальная модель линейной регрессии для прогнозирования продукции растениеводства имеет вид: у = 145,31е0,1566х с коэффициентом детерминации 95,29%, точна для прогноза на короткую перспективу в силу ее экспоненциального сильного роста. При этом было выявлено в ходе построения модели регрессии: Pr = 47,8949 × U - 734,688, что урожайность определенно влияет на результирующий показатель отрасли.

Анализируя животноводство, была выявлена прямая связь между продукцией и расходованием кормов: Pj = 9,55163 × R – 877,522, что отражает ту часть за- трат, приходящихся на предприятия в исследуемой отрасли сельского хозяйства. Также очевидно, что продукция от животноводства легко описывается линейной моделью с высокой точностью в 99,55% и имеет уравнение: у = 11,576% + 40,833.

Наряду с линейными моделями особо проявили свою практическую применимость модели Брауна и Хольта-Винтерса. Определенный тренд на будущий период уже имеет черты поэтапного и равномерного роста. В случае с прогнозом растениеводства наблюдается уже более качественный прогноз, динамика которого аналогична ретроспективным данным. Стоит отметить высокую точность моделей. Среднее абсолютное отклонение (MAD) имеет низкие значения, а высчитанные коэффициенты детерминации, равные 92,1 и 99,26%, подтверждают высокую точность.

Итогом моделирования нейронной сети стал еще более адекватный и точный прогноз производства крестьянских (фермерских) хозяйств до 2030 года. Обучение нейронной сети позволило выявить все колебания ряда и определило входные коэффициенты, что позволило осуществить данный прогноз.

Применение эконометрических моделей позволит как государству, так и отдельным организациям проанализировать ситуацию в какой-либо сфере и принять соответствующие решения. В настоящее время сельское хозяйство является одним из приоритетных направлений развития. Таким образом, приведенные в данной статье модели информативны, широко применимы и универсальны, в дальнейшем могут быть использованы для характеристики отрасли сельского хозяйства и сфер АПК страны.