Экономико-кибернетическая система затрат в управлении инновационно-инвестиционными процессами

Экономическая политика, пожалуй, каждого промышленного предприятия направлена на инновационный путь развития. Эволюционный переход России от плановозатратной к рыночной экономике формирует новую парадигму управленческой природы затрат [2]. Структура парадигмы раскрывается через предприятие-объект как сложную замкнутую управляемую экономикокибернетическую производственную систему с обратными связями (ЭКС затрат), создающую добавленную стоимость - S (рис. 1), которая включает:

• 1)    объект управления ОУ (предприятие) -операционную производственную подсистему, трансформирующую материальные, трудовые, основные, финансовые и прочие затраты ограниченных ресурсов на «входе» в готовую продукцию, работы и услуги в рамках мониторинга оперативного бенчмаркинга, обеспечивающего организационно-экономический сервис менеджменту для достижения целей на «выходе». В этом блоке приведена производственная функция затрат на входе Q_c + ^ Qm х ^УоУ, передаточная функция производственной подсистемы которой *Н$‘Р№!” ^{66 выходные} параметры добавленной стоимости S, рис. 1 -центральный блок;

• 2)    подсистему управления ОУ как подсистему мониторинга стратегического бенчмаркинга, обеспечивающую оптимальную

концепцию ЭКС затрат, направленной на выработку сбалансированных показателей и применение стратегических методов принятия решений (рис. 1 - верхний блок) обеспечивает в системе отрицательную обратную связь на основе стратегических затрат ОУ как коэффициент - мультипликатор отрицательной обратной связи в кибернетической системе имеет вид множителя Кейнса1

11 ®{д) 1-£

• 3)    определяющую подсистему «научно-

• технического развития», генерирующую стратегию перспективного расширенного инновационного развития, механизмы и методы, направ

ленные на повышение ценности и надежности хозяйственной деятельности (см. рис. 1) [3].

Нижний блок на рис. 1 обеспечивает в системе положительную обратную связь на основе амортизационного интегратора-ускорителя ОУ с применением множителя Ломанна-Рухти2

/2:

— = Vxexp7 =

2x7

7 + 1

Устойчивость управляемой ЭКС затрат обеспечивается только в замкнутых целевых производственных системах. В разомкнутых

И. Подсистема управления ОУ:

«Стратегический бенчмаркинг»

мультипликатор- коэффициент отрицательной обратной связи:

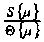
I. Производственная подсистема:

«О б ъ е к т управления»

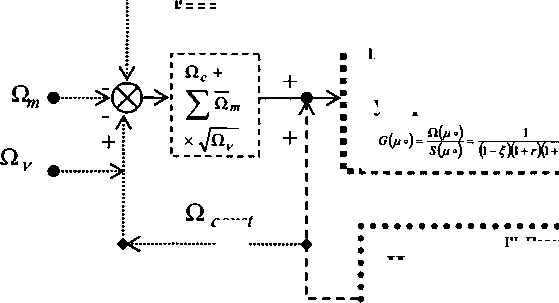
const

0=7+5

5 =

3,Н,1Г

III. Подсистема:

Научно-технического развития

Амортизационный интеграатор положительной обратной связи:

^T₍W _w [2хГ

— = V х exp J =--

{ dt         lr+i

S"

Рис. 1. Экономико-кибернетическая система затрат

S'

неуправляемых производственных системах неизбежен кризис, спад, рецессия, так как ей (системе) не свойственно целевое функционирование. «Теория производства охватывает экономические процессы, связанные с изготовлением (созданием) материальных благ, прежде всего - количественные отношения между благами, вовлекаемыми в процесс производства («вход»), и благами, получаемыми в результате этого процесса («выход»)»³. Различают следующие известные производственные функции⁴, отражающие взаимосвязи между входом вовлекаемых благ (факторов производства - г ) и выходом произведенных благ (продуктов - х): а) Кобба-Дугласа; б) функция постоянной эластичности замены (CES); в) функция Леонтьева; г) производственная функция фон Тюнена:

х = с₀ + qVr, где с_о,с_х = const.

В экономических системах за основу модели трансформации операционных затрат в условно-чистую продукцию можно условно с достаточной вероятностью утверждать и принять производственную функцию объема продукции типа «А» Иоганна фон Тюнена5, ха- рактер которой прогрессивно-регрессивный при ограничениях натуральных единиц X как функция от числа работников г: K = C0+C1xVr; Со, С) = const; К = /(г). В авторской модели принятоQ = /(£), при заданном количестве рабочих машин, оборудования Со, материальных и других ресурсов Ci, {Со; Ci} = const. Совокупные операционные затраты Q = Qe + Qv + Qm преобразуем в функцию затрат при производстве продукции с учетом закона убывающей доходности:

Q~f Пс+^Птх^к/ = 1, 2, где Qc = const - накладные затраты фирмы на содержание и реновацию основного капитала; Qm = const - средние материальные затраты на единицу продукции; Qv - затраты на оплату труда;

q=№.

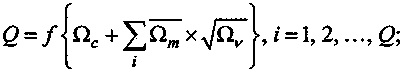
Qc - const; QOT - const.

Поведенческая производственная модель трансформации операционных затрат в экономических системах построена на основе алгоритма управленческих параметров (см. таблицу), где дан расчет выручки W = P*Q от реа- лизации продукции д по цене Р как производственная функция в виде дифференциала с одной стороны

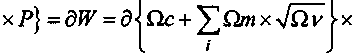
xd(l + 91)xa(l + A),z = l,2,...,£, где А - ставка НДС и добавленная стоимость как целевая функция универсального типа, сочетающая в себе интересы государства (налоги), наемных работников и менеджеров (оплата труда), собственников (чистого дохода в виде амортизации и прибыли) с другой:

хV^v >х х (1 + 91) х (1 + А) - ^ Qm -> шах 5.

Структура предельной 88 = д < Ос + VO у +

+91 +AS} представляет собой меру прироста основного капитала амортизации Ос, прироста переменного капитала на оплату труда VOv , прибыли при заданной рентабельности 91 и НДС, AS.

Соотношение e = /joc+^Omx7o7 ,z = l,2,...,g и добавленной стоимости 8 = дхР-^От, а также экономико-математическая модель поэтапного превращения затрат в добавленную стоимость для оценки максимальной целевой функции можно отразить в виде поведенческого алгоритма (см. таблицу). Откуда поведение добавленной стоимости в неуправляемой ЭКС системе неуклонно стремится к рецессии (рис. 2) и иллюстрирует закон убывающей доходности затрат

S = * Oc + ^OmxyjOv

х(1 + 9i) х (1 + А) - ^ От -> min 8 ⁶.

Целевая функция достигнет максимума (S—> max ) в точке, где соблюдаются ограничения в системе и будет расти.

Поведенческий алгоритм трансформации поэтапного превращения затрат в добавлен-

6 Закон убывающей доходности затрат

5 = < Ос + ^От х VOr м 1 + Я)(1 + Д) - ^Ощ —> min S.

ную стоимость реализуется в виде решения задачи динамического программирования: операционные затраты - оптимальная условно-чистая продукция и далее спад.

1-й шаг (1-й ряд -х) «Ускорение объемов производства» в промежутке / от 1 до 6: как средняя скорость роста производительности труда и ускорение предельных объемов произ- водства на участке

t^ 1-6}   до точки

ад „ а2д п

— >0; —>0 для аь ы?

перегиба на кри- вой Q = С0 + Сх х -JL ; рост средней и ускорение предельной добавленной стоимости наблюдает ся на участке /{1—6} как —>0; —т- = 0для 8L 8L2

/{1-6} до той же точки перегиба на кривой S = QxP- От ; Совокупные издержки растут замедленными темпами £Q =//{1-6}; средние прямые затраты на короткий период

5Q п равны и постоянны ^^>0=const, предельные накладные и предельные общие затраты сни-82ОС а d2Q п тт жаются ---:г<0; —-<0. На участке [I; 6]

sg² ад^{2 3}

прибыль меняет знак от R < 0 на 7?> 0. Средняя =591 и предельная рентабельность возрастают ^^>0,

329l п            „„5

---->0 с 3-го шага. В точке t =7----

= 0 при-

dQ2

aQ2

быль достигает максимума и меняет знак пре,а дельная рентабельность< 0.

ао2

2-й шаг в точке объема продукции QV = 6} «Минимум прямых затрат»: Точка перегиба прямых затрат, в точке / = 6 они ми-а2о _ нимальны, предельные равны—т=0, после ад2

г                52О _ точки / >6 они начнут расти 2 >0; удельные

ЭОс _ затраты - косвенные снижаются---<0 и по-ад еле точки t > 6.

3-й шаг «Замедление темпов» в промежутке точек g^t = 7-10}. Экономическая производственная мощность отражает экономическую добавленную стоимость и характеризуется замедлением темпов роста физических объемов производства от точки 6, но валовые

ю

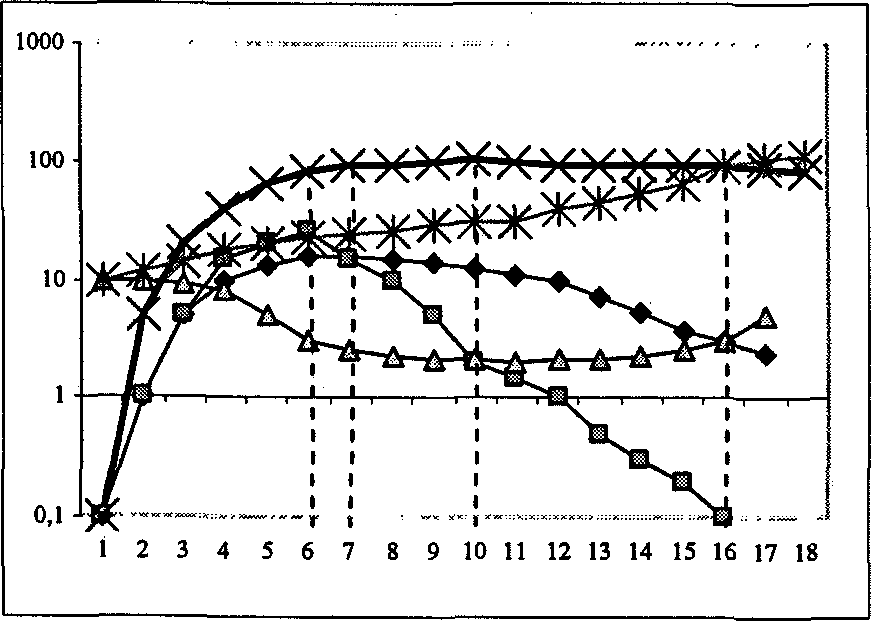
Рис. 2. Модель управленческого поведения ЭКС затрат

Целевая передаточная функция ЭКС затрат:

S = ■ Qc + ^Q/их VOv i

-x(l + max 8^Т^ , при условиях:

Sx(n-H)               Z5x(g„5±AgK)-A3c±AQp

1 J ЫГуО — ,        _{4 z}¹     ," —^ tv), 01 , ^J Z-lYT ”

(5-5_о)х(П-Н-Д)                   Qn6 + kQnp

^Гг^ 2 at

= VxexpJ =

п >

7; 4) 1ипС, J^TA^-K.)

L тх

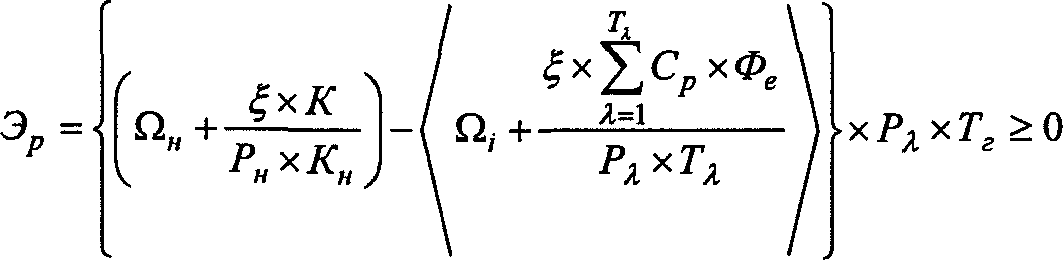
5) 88 = 8f - Qc + ^Омх VOv -xd(l + 9t)xd(l + A)-9^Qm = 0 .

Условные обозначения на рис. 2 (сверху вниз): (1-й ряд -х) - условно-чистая добавленная стоимость S;

I

d(l + 9t')x5(l + A)-d^Q/n = 0; как производственная функция операционных затрат и объема продукции типа А натуральных

единиц от числа работников Q = f (I?) , при заданном количестве рабочих машин, оборудования С_о, материальных и других ресурсов С_ь {С_о; Ci}=const;

\с = const; Qm = const; (2-й ряд- ж )- совокупные затраты Q = Qc + Q v + Ом, преобразующие предметы труда в гото-

Вестник ЮУрГУ, № 30, 2008

/

вую продукцию с учетом закона убывающей доходности Q = f - Q_c + ^Q х ^Q^

1 m

•₅i = 1,2,..., 5, где Q_c - const - накладные затраты фирмы на содержание и

реновацию основного капитала; Qm = const - средние материальные затраты на единицу продукции; Qv - затраты на оплату труда; (3-й ряд - □) - предельная производительность труда, оценивается как д2Т =    • (4-й ряд - 0) - средний доход как производительность труда ЭТ = — ; (5-й ряд - А) - средние операци-

SL

онные затраты Q = —

Управление инвестициями и инновационной деятельностью

Алгоритм оценки некоторых поведенческих параметров

L Q Q Q Q Q ^v+m Q 8Q 50 9L s2e 91? W S SR 0 0 200 0 0 0 0 -200 1 5 350 70 40 30 30 5 5 150 100 -200 2 20 600 30 10 20 16,67 10 15 600 400 0 3 40 900 22,5 5 17,5 15 13,3 20 1200 800 300 4 65 1250 19,23 3,1 16,15 14 16,25 25 1950 1300 700 5 80 1750 21,88 2,5 19,37 33,33 16 15 2400 1600 650 6 90 2000 22,22 2,2 20 25 15 10 2700 1800 700 7 95 2200 23,16 2,1 21,05 40 13,57 5 2850 1900 650 8 97 2370 24,43 2,05 22,37 85 12,12 2 2860 1940 540 9 99 2990 30,2 2 28,18 310 11 2 2970 1980 -20 10 97 3170 32,68 2,05 30,61 90 9,7 -2 2910 1940 -260 объемы растут, и наращивается тельность до точки t<1, — >0, 9L производительность начинает производи-

предельная

снижаться

d2Q .

—2-<0, предельные издержки меняют знак с минуса на плюс -—^>0. Замедление средней и предельной добавленной стоимости наблюдается на участке Z{7—10} как —>0;

9L g2 8

—— <0. Максимальная прибыль фирмы дос 91?

тигается вторично в районе точки 10 при поведении предельной рентабельности от

---->0 и равенстве в точке 10----= 0 и по- ЭП₂                      5Q₂

5291 .

еле----< 0.

9Q2

4-й шаг «Рост технический» в промежутке точек QV ⁼ Ю-12} «Техническая мощность или производственный потенциал»: максимальный объем продукции достигается в точках 10-12. Наблюдается рост объемов производства, производительность труда как средняя, так и предельная снижаются ^~< 0;

—^-<0 для /{10-12} до точки перегиба на 91?

кривой Q = С_О + С, х -Jb ;

Предельная добавленная стоимость изме-S няется от --->0 и равна, в точках /{10-

9Q2

-12}— = 0 8Q₂

Qc = const; Qm = const ;

S = QxP -^Q_m —>max S или

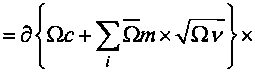
x3(l + 9T) x 9(1 + Д) - Э^О/и < 0.

i g2^

В точке t = 10---< 0 прибыль достигает ми- dQ2

нимума и меняет знак предельная рентабель-д291 _ „ ность----< 0. Наступает производственная и

9Q2

социальная стагнация.

5-й шаг в промежутке точек Q^t = 12-16} «Экономический спад-торможение системы»: наступает после точки / > 12. Резко нарастает убыток, предельные и средние издержки воз-

52Q 5Q               _ растают —т>0; —>0. Предельная добав-

8Q1 8Q к ленная стоимость равная в точке t = 12

92S

9Q2

=0, Q-f' O-cA-^Qm^^ -,z = l,2,...,g достигает границу максимальной, чистой стоимости

S = Q х Р - ^П_т = max S, так как еще соблюдается равенство

5(1 + 9Г)х xd(l +A)-d^Qzn = 0. i

После точки Z — 12 темпы прироста чистой

52А п стоимости становятся отрицательными---< 0.

9Q2

Совокупные, предельные и удельные затраты dQ п д2П п растут с ускорением ^^ »0, —- »0.

• -^^»0’ Точка t = 16 представляет собой затратно-ценовой кризис. Депрессия достигает кульминационного периода, рис. За. Устойчивость ЭКС обеспечивается только в управляемой системе на основе целевой передаточной

Ж                                   Бенчмаркинг стратегических затрат-2

(новый уровень)

• б) Бенчмаркинг '^                         ^S^ ^С°^П51^^таХ

стратегических затрат-1 /, Амортизационный z z

(первый уровень) / / интегратор ,* ,*

• а)    ,..•••'*'"                                                 "    8'^-» min

____________________________________________________________________________ Т, лет

Рис. 3. Модель управленческого поведения добавленной стоимости 8^ :

• а)    рецессия в неуправляемой, разомкнутой ЭКС системе - 8'^ ->min ;

• б)    в управляемой ЭКС системе с обратными связями s(t\ = const -> max

  

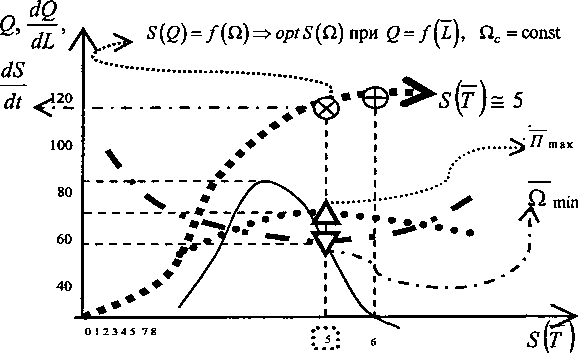
  Рис. 4. Устойчивый оптимум системы ЭКС-5, где» ■■■■■■■■ - производственная функция добавленной стоимости:

  
  

S (2) = / (fl) => optimum, 8 (Я) при Q = f (2,) , Я_с = const ;

• — . . — - средняя производственная себестоимость Я = — -»min на 5-м шаге;

„ dQ Дб

____- предельная производительность труда <ШТ = — » ——;

dL kL

............ - средняя производительность труда П = — => max , при Яс = const функции, рис. 36:

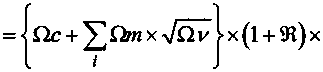
х (1 + А) - ^ £1?и-> max ^Т).

i

Устойчивый оптимум в ЭКС системе достигается состоянием 5, рис. 4. Траектория поступательного расширенного экономического развития заложена не только в чистой прибыли, но и в составе и структуре основного капитала, то есть в амортизационной и научнотехнической политике предприятия, обеспечивающей устойчивое не циклическое развитие всей системы, которая и представляет третий блок в ЭКС затрат.

Бенчмаркинг стратегических затрат стабилизирует выходные параметры ЭКС (отрицательная обратная связь), а амортизационный интегратор способен вывести ее (систему) на совершенно новую ступень экономиче ского развития (положительная обратная связь), и не допустить ожидаемой рецессии.

Бенчмаркинг стратегических затрат стабилизирует выходные параметры ЭКС (отрицательная обратная связь), а амортизационный интегратор способен вывести ее (систему) на совершенно новую ступень экономического развития (положительная обратная связь), и не допустить ожидаемой рецессии.